Думал тут над одной проблемой, и в очередной раз понял, что математика - это все же безумно, неописуемо круто

Думал тут над одной проблемой, и в очередной раз понял, что математика - это все же безумно, неописуемо круто. Мало что столь же важно, как она. И как же много есть чисто практических проблем, которые мы никак не можем решить из-за того, что не имеем решения чисто теоретических математических проблем.

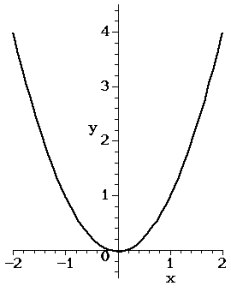
Если конкретно, то думал я над тем, как можно найти глобальный максимум у функции в многомерном пространстве. Поясню издалека. Вот есть у нас например классическая convex-функция под названием парабола, y = x^2. Вот ее график, на первой картинке. Где ее самое маленькое значение? Посмотрев на график вы сразу ткнете пальцем где. Возьмем более сложный случай, когда у нас есть параболоид, считай парабола в трех измерениях, где значение функции z = x^2 + y^2 и зависит от двух параметров. Вот и она, на второй картинке. Опять, тот же вопрос - где ее минимум? Снова, посмотрев на картинку мы можем ткнуть пальцем и сказать, где же он. Но что если у нас функция не в двух измерениях а например в тысячемерном пространстве? Или вообще имеет миллион измерений? Ее уже не нарисуешь, и вот так по картинке минимум не найдешь. Очевидно, для этого в математике придумали кучу всяких методов для нахождения минимума аналитически. Ну, берет математик, пишет несколько формул и сразу вам говорит где минимум. Все здорово. Если хочется находить такой минимум автоматически - тоже не вопрос, это можно делать с помощью алгоритмов, которые легко программируются. Есть например инкрементальные квазиньютоновские алгоритмы вроде BFGS или adagrad. Есть в конце-концов т.н. градиентный спуск. Звучит страшно, но по сути их идея в том, чтобы в каждом измерении просто катиться вниз по склону функции до тех пор, пока мы не спустимся туда, где во всех измерениях нам пришлось бы идти вверх чтобы с места сдвинуться. Ну как представьте что вы уселись на склон параболоида и покатились вниз. Пока все хорошо, никаких проблем, можно это делать с любым количеством измерений и не мучиться. Но что если наша функция non-convex, как на третьей картинке? Там много таких "оврагов". Уселись мы куда-то на склоне и покатились вниз. Прикатились на дно одного оврага, но мы же не можем быть уверены что мы спустились максимально низко. Может, если мы покатимся из другой точки или в другом направлении то сможем спуститься ниже. А если у нас еще и миллион измерений? Как искать т.н. глобальный минимум, самое минимальное значение у такой функции?

Вот задумался я над этим, и выяснил, что эта задача (нахождение глобального минимума non-convex функции во множестве измерений) не имеет нормального решения. Мы можем найти локальный минимум с помощью тех алгоритмов, что я упоминал (скатиться на дно одного из оврагов) но вот точно найти самый минимум мы не можем. Никак (если у нас нет внятной формулы, которая описывает функцию и мы можем только посчитать ее значение в конкретной точке)

И вот тот, кто придумает как это сделать и придумает для этого универсальный алгоритм - реально озолотится и сильно продвинет все человечество вперед. Почему? Ну, пример, который близок мне - системы машинного обучения, искусственный интеллект. Вся суть машинного обучения, на самом деле, это поиск минимума так называемой "функции стоимости". Не буду вам забивать голову, лишь скажу, что когда где-то есть ИИ то все его обучение заключается в том, чтобы найти минимум у его функции стоимости. Чем хуже мы находим минимум - тем больше вероятность ошибки. А чем черевата ошибка ИИ? Ну например автопилот Tesla недавно ошибся. И принял грузовик за дорожный знак, что убило его водителя. Если бы ИИ был лучше обучен - ошибки бы не было. А до тех пор, пока мы не умеем хорошо искать минимумы - не будет у нас нормальных беспилотных машин. Полноценного ИИ, который можно быстро обучить. Настоящих андроидов, как в фантастических фильмах. А ведь все лишь из-за каких-то математических уравнений, задачек, которые мы решать пока не научились.

Вот такие дела. И ведь я привел только один пример. А сколько еще таких нерешенных задач есть? И сколько крутых вещей может появиться если их решить?

Так что очень уж раздражают люди, которые заявляют, что умение решать математические задачи никому не нужно и вообще математика это унылая теория, не имеющая отношения к реальности. Такие люди просто не понимают, насколько сильно все зависит от математики.

P.S. Просьба к тру-математикам не кидаться помидорами. Я вкурсе, что я все очень сильно упростил.

Комментарии: