Теорема Байеса: просто о сложном

Перевод статьи Bayes’ rule with a simple and practical example под авторством Tirthajyoti Sarkar. Разрешение автора на перевод получено. Мне данная статья понравилась лаконичностью и интересным примером из жизни. Надеюсь, будет полезна и Вам.

В статье продемонстрируем применение Теоремы Байеса на простом практическом примере с использованием языка программирования Python.

Теорема Байеса

Теорема Байеса (или формула Байеса) - один из самых мощных инструментов в теории вероятностей и статистики. Теорема Байеса позволяет описать вероятность события, основываясь на прошлом (априорном) знании условий, которые могут относиться к событиям.

Например, если заболевание связано с возрастом, то, используя теорему Байеса, возраст человека можно использовать для более точной оценки вероятности заболевания по сравнению с оценкой вероятности заболевания, сделанной без знания возраста человека.

Теорема Байеса позволяет учитывать субъективную оценку или уровень доверия в строгих статистических расчетах. Это один из методов, который позволяет постепенно обновлять вероятность события по мере поступления новых наблюдений или сведений.

Историческая справка

Теорема Байеса названа в честь преподобного Томаса Байеса. Он первым использовал условную вероятность для создания алгоритма (Proposition 9), который использует вероятность для вычисления пределов неизвестного параметра ( опубликовано в «An Essay towards solving a Problem in the Doctrine of Chances»). Байес расширил свой алгоритм на любую неизвестную предшествующую причину.

Независимо от Байеса, Пьер-Симон Лаплас в 1774 году, а затем в своей «Аналитической теории вероятностей» (1812 года) использовал условную вероятность, чтобы сформулировать отношение обновленной апостериорной вероятности к априорной вероятности при наличии данных.

Теорема Байеса позволяет учитывать субъективную оценку или уровень доверия в строгих статистических расчетах.

Логический процесс для анализа данных

Мы начинаем с гипотезы и уровеня доверия к этой гипотезе. Это означает, что на основе знания предметной области или предшествующих других знаний мы приписываем этой гипотезе ненулевую вероятность.

Затем мы собираем данные и обновляем наши первоначальные убеждения. Если новые данные подтверждают гипотезу, то вероятность возрастает, если не подтверждают - вероятность снижается.

Звучит просто и логично, неправда ли?

Исторически в большинстве методах статистического обучения статистических исследований понятие априорного события не используется или недооценивается. Кроме того, вычислительные сложности байесовского обучения не позволяли ему стать мейнстримом более 200 лет.

Но сейчас все меняется с появлением байесовского статистического вывода ...

Если новые данные подтверждают гипотезу, то вероятность возрастает, если не подтверждают - вероятность снижается.

Байесовский статистический вывод

Байесовская статистика и моделирование возродились благодаря развитию искуственного интеллекта и систем машинного обучения на основе данных в бизнесе и науке.

Байесовский вывод применяется в генетике, лингвистике, обработке изображений, визуализации мозга, космологии, машинном обучении, эпидемиологии, психологии, криминалистике, распознавании человека, эволюции, визуальном восприятии, экологии и во многих других областях, где большую роль играют извлечение информации из данных и предиктивная (прогнозная) аналитика.

Байесовская статистика и моделирование возродились благодаря развитию искуственного интеллекта и систем машинного обучения на основе данных в бизнесе и науке.

Примеры с кодом на Python

Скрининг-тест на употребление наркотиков

Мы применим формулу Байеса к скрининг-тесту на употребление наркотиков (который бывает обязательным для допуска к работе на федеральных или других должностях в компаниях, которые обещают рабочую среду, свободную от наркотиков).

Предположим, что тест на применение наркотика имеет 97% чувствительность (комментарий переводчика - по сути это доля истинно положительных результатов) и 95% специфичность (комментарий переводчика - по сути это доля истинно отрицательных результатов). То есть тест даст 97% истинно положительных результатов для потребителей наркотиков и 95% истинно отрицательных результатов для лиц, не употребляющих наркотики. Эта статистика доступна при тестировании тестов в исследовании до вывода их на рынок. Правило Байеса позволяет нам использовать такого рода знания, основанные на данных, для расчета окончательной вероятности.

Предположим, мы также знаем, что 0,5% населения в целом употребляют наркотики. Какова вероятность того, что случайно выбранный человек с положительным результатом анализа является потребителем наркотиков?

Обратите внимание, что это важнейшая часть «априорной вероятности», которая представляет собой часть обобщенных знаний об общем уровне распространенности. Это наше предварительное суждение о вероятности того, что случайный испытуемый будет употреблять наркотики. Это означает, что если мы выберем случайного человека из общей популяции без какого-либо тестирования, мы можем только сказать, что вероятность того, что этот человек употребляет наркотики, составляет 0,5%.

Как же тогда использовать правило Байеса в этой ситуации? Мы напишем пользовательскую функцию, которая:

• принимает в качестве входных данных чувствительность и специфичность теста, а также предварительные знания о процентном соотношении потребителей наркотиков

• и выдает вероятность того, что тестируемый является потребителем наркотиков, на основе положительного результата теста.

Вот формула для вычисления по правилу Байеса:

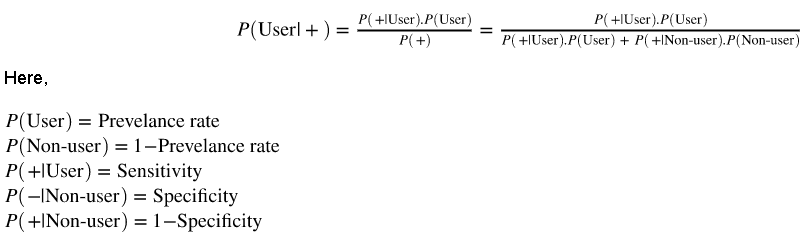
Код выложен здесь. Если мы запустим функцию с заданными данными, мы получим следующий результат:

Что здесь интересного?

Даже при использовании теста, который в 97% случаях верно выявляет положительные случаи и который в 95% случаях правильно выявляет отрицательные случаи, истинная вероятность быть наркоманом с положительным результатом этого теста составляет всего 8,9%!

Если вы посмотрите на расчеты, то станет понятным, что это связано с чрезвычайно низким уровнем распространенности. Количество ложных срабатываний превышает количество истинных срабатываний.

Например, если протестировано 1000 человек, ожидается, что будет 995 не наркоманов и 5 наркоманов. Из 995 не наркоманов ожидается 0,05 ? 995 ? 50 ложных срабатываний. Из 5 наркоманов ожидается 0,95 ? 5 ? 5 истинно положительных результатов. Из 55 положительных результатов только 5 являются истинно положительными!

Посмотрим, как вероятность меняется с уровнем распространенности (код).

Обратите внимание, что в данном случае наше решение зависит от порога вероятности. В данном примере он установлен на уровне 0,5. При необходимости его можно понизить. При пороге 0,5 у нас должен быть уровень распространенности почти 4,8%, чтобы поймать наркомана с одним положительным результатом теста.

Какой уровень точности теста необходим для улучшения сценария?

Мы увидели, что чувствительность и специфичность теста сильно влияют на вычисления. В таком случае нам может быть интересно узнать, какая точность теста необходима для повышения вероятности выявления наркоманов (код здесь).

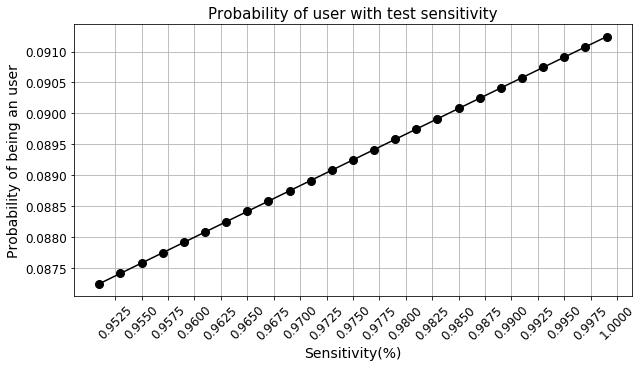
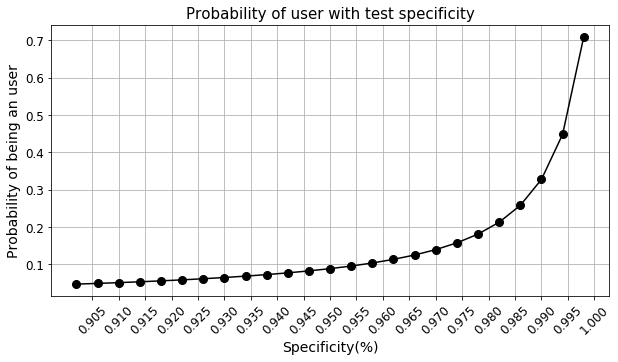
На графиках видно, что даже с чувствительностью, близкой к 100%, мы ничего не выигрываем. Однако имеет место нелинейная зависимость вероятности от специфичности теста, и по мере того, как тест достигает совершенства (с точки зрения специфичности), мы получаем значительное увеличение вероятности. Следовательно, все усилия Отдела разработки (R&D) должны быть направлены на улучшение специфичности теста.

Этот вывод можно интуитивно сделать из того факта, что основной проблемой, связанной с низкой вероятностью, является низкий уровень распространенности. Следовательно, нам следует сосредоточить внимание на правильном отлове не наркоманов (т.е. улучшении специфичности), потому что их намного больше, чем наркоманов.

Отрицательных примеров в этом примере гораздо больше, чем положительных. Таким образом, специфичность теста должна быть максимальной.

Цепочка расчетов и формула Байеса

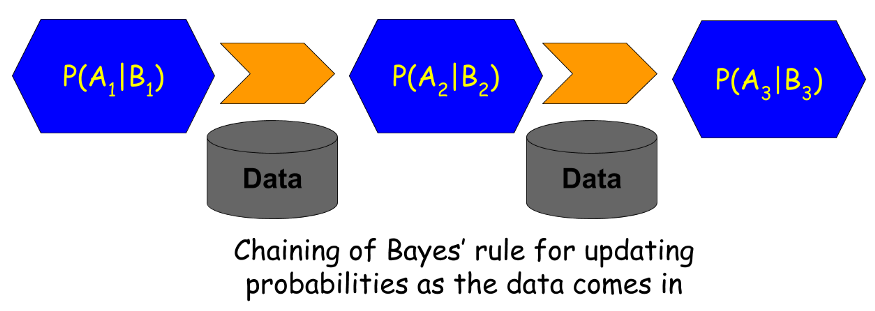
Лучшее в байесовском выводе - это возможность использовать предшествующие знания в форме априорного вероятностного члена в числителе теоремы Байеса.

В данной постановке процесса скрининга наркотиков предварительные знания - это не что иное, как вычисленная вероятность теста, которая затем возвращается к следующему тесту .

Это означает, что для этих случаев, когда уровень распространенности среди населения в целом чрезвычайно низок, один из способов повысить уверенность в результате теста - назначить последующий тест, если первый результат теста окажется положительным.

Апостериорная вероятность первого теста становится априорной вероятностью для второго теста, т.е. P (Наркоман) для второго теста уже не общий показатель распространенности, а вероятность из первого теста.

Вот пример кода для демонстрации цепочки.

p1 = drug_user(   prob_th=0.5,   sensitivity=0.97,   specificity=0.95,   prevelance=0.005) print("Probability of the test-taker being a drug user, in the first round of test, is:",       round(p1,3)) print() p2 = drug_user(   prob_th=0.5,   sensitivity=0.97,   specificity=0.95,   prevelance=p1) print("Probability of the test-taker being a drug user, in the second round of test, is:",       round(p2,3)) print() p3 = drug_user(   prob_th=0.5,    sensitivity=0.97,   specificity=0.95,   prevelance=p2) print("Probability of the test-taker being a drug user, in the third round of test, is:",       round(p3,3))

После отработки кода мы получаем следующее:

Когда мы выполняем тест в первый раз, расчетная (апостериорная) вероятность низка, всего 8,9%, но она значительно возрастает до 65,4% во втором тесте, а третий положительный тест дает апостериорную вероятность 97,3%.

Следовательно, неточный тест можно использовать несколько раз, чтобы обновить наше мнение с помощью последовательного применения правила Байеса.

Лучшее в байесовском выводе - это возможность использовать предшествующие знания в форме априорного вероятностного члена в числителе теоремы Байеса.

Резюме

В этой статье мы рассказываем об основах и применении одного из самых мощных законов статистики - теоремы Байеса. Продвинутое вероятностное моделирование и статистический вывод с применением теоремы Байеса захватили мир науки о данных и аналитики.

Мы продемонстрировали применение правила Байеса на очень простом, но практичном примере тестирования на наркотики и реализовали расчеты на языке програмирования Python. Мы показали, как ограничения теста влияют на прогнозируемую вероятность и что в тесте необходимо улучшить, чтобы получить результат с высокой степенью достоверности.

Мы также показали истинную силу байесовских рассуждений и как несколько байесовских вычислений можно объединить в цепочку, чтобы вычислить общую апостериорную вероятность.

Для дальнейшего чтения автор рекомендует:

1. https://www.mathsisfun.com/data/bayes-theorem.html

2. https://betterexplained.com/articles/an-intuitive-and-short-explanation-of-bayes-theorem/