Как работают квантовые компьютеры. Собираем паззл

Квантовые компьютеры и квантовые вычисления — новый баззворд, который добавился в наше информационное пространство наряду с искусственным интеллектом, машинным обучением и прочими высокотехнологическими терминами. При этом мне так и не удалось найти в интернете материал, который бы сложил у меня в голове пазл под названием “как работают квантовые компьютеры”. Да, есть много прекрасных работ, в том числе и на хабре (см. Список ресурсов), комментарии к которым, как это обычно и бывает, еще более информативны и полезны, но картинка в голове, что называется, не складывалась.

А недавно ко мне подошли коллеги и спросили “Ты понимаешь как работает квантовый компьютер? Можешь нам рассказать?” И тут я понял, что проблема со складыванием в голове целостной картинки есть не только у меня.

В результате была сделана попытка скомпилировать информацию о квантовых компьютерах в непротиворечивую логическую схему, в которой бы на базовом уровне, без глубокого погружения в математику и структуру квантового мира, объяснялось что такое квантовый компьютер, на каких принципах он работает, а также какие проблемы стоят перед учеными при его создании и эксплуатации.

Дисклеймер

(к оглавлению)

Автор не является специалистом в квантовых вычислениях, и целевая аудитория статьи — такие же ИТ-шники, не квантовые специалисты, которые тоже хотят собрать в голове картинку под названием “Как работают квантовые компьютеры”. Из-за этого многие понятия в статье сознательно упрощены для лучшего понимания квантовых технологий на “базовом” уровне, но без совсем уж сильного упрощения с потерей информативности и адекватности.

В статье, в некоторых местах используются материалы из других источников, список которых приведен в конце статьи. Везде где это было возможно, вставлены прямые ссылки и указания на оригинал текста, таблицы или рисунка. Если где-то что-то (или кого-то) забыл, пишите — поправлю.

Введение

(к оглавлению)

В этой главе мы коротко рассмотрим с чего началась квантовая эра, что явилось побудительной причиной для возникновения идеи квантового компьютера, кто (какие страны и корпорации) в настоящее время являются ведущими игроками на этой поляне, а также вкратце поговорим об основных направлениях развития квантовых вычислений.

Как все начиналось

(к оглавлению)

Точкой отсчета квантовой эры принято считать 1900 год, когда М. Планк впервые выдвинул гипотезу о том, что энергия испускается и поглощается не непрерывно, а отдельными квантами (порциями). Идею подхватили и развили многие выдающиеся ученые того времени — Бор, Эйнштейн, Гейзенберг, Шредингер, что, в конечном счете, привело к созданию и развитию такой науки как квантовая физика. Про становление квантовой физики как науки в Сети есть много хороших материалов, в этой статье мы не будем подробно останавливаться на этом, но указать дату, когда мы вошли в новую квантовую эпоху, было необходимо.

Квантовая физика принесла в нашу обычную жизнь много изобретений и технологий, без которых сейчас трудно себе представить окружающий мир. Например, лазер, который сейчас используется везде, от бытовой техники (лазерные нивелиры и прочее) до высокотехнологичных систем (лазеры для коррекции зрения, привет meklon ). Логично было бы предположить, что рано или поздно кто-то выдвинет идею о том, что почему бы не использовать квантовые системы для вычислений. И вот в 1980 году это случилось.

Википедия указывает на то, что первым идею квантовых вычислений высказал в 1980 году наш ученый Юрий Манин. Но реально заговорили о ней только в 1981, когда небезызвестный Р. Фейнман в докладе на первой конференции по физике вычислений, проведенной в Массачусетском технологическом институте, отметил, что невозможно моделировать эволюцию квантовой системы на классическом компьютере эффективным способом. Он предложил элементарную модель квантового компьютера, который будет способен провести такое моделирование.

В Сети есть вот такая работа, в которой хронология развития квантовых вычислений рассматривается более академически и подробно, мы же пробежимся коротко:

Основные вехи в истории создания квантовых компьютеров:

• [1994]. П.Шор. Разработан квантовый алгоритм факторизации чисел
• [1998]. Создан первый 2-х кубитный квантовый компьютер
• [2001]. IBM представил выполнение алгоритма Шора для разложения числа 15
• [2007-2016]. D-Wave создает и развивает компьютер с 128-2000 кубитов
• [2012]. В Университете Калифорнии реализовали алгоритм Шора для числа 21
• [2016]. Google смоделировал молекулу водорода на 9-и кубитном компьютере
• [2017]. IBM смоделировала гидрид бериллия BeH2 (три атома)
• [2019]. IBM Q System One. 20-и кубитный компьютер в облаке
• [2019]. Google Sycamore. 53-х кубитный компьютер. Квантовое превосходство?

 

Как вы видите прошло 17 лет (с 1981 до 1998) с момента идеи до ее первой реализации в компьютере с 2-мя кубитами, и 21 год (с 1998 до 2019) до момента, когда количество кубитов увеличилось до 53-х. Потребовалось 11 лет (с 2001 до 2012) чтобы улучшить результат выполнения алгоритма Шора (мы остановимся на нем подробнее чуть далее) с числа 15 до 21. Также только три года назад мы подошли к тому, чтобы реализовать то, о чем говорил Фейнман, и научиться моделировать простейшие физические системы.

Развитие квантовых вычислений идет медленно. Перед учеными и инженерами стоят очень сложные задачи, квантовые состояния очень недолговечны и хрупки, и, чтобы сохранить их достаточно долгое время для выполнения вычислений, приходится строить саркофаги за десятки миллионов долларов, в которых поддерживается температура чуть выше абсолютного ноля, и которые максимально защищены от внешних воздействий. Далее мы будем говорить об этих задачах и проблемах более подробно.

Ведущие игроки

(к оглавлению)

Слайды для этого раздела взяты из статьи Квантовый компьютер: большая игра на повышение. Лекция в Яндексе, от научного сотрудника Российского квантового центра Алексея Фёдорова. Позволю себе прямые цитаты:

Все технологически успешные страны в данный момент активно занимаются развитием квантовых технологий. В эти исследования вкладывается огромное количество средств, создаются специальные программы поддержки квантовых технологий.

В квантовой гонке участвуют не только государства, но и частные компании. Суммарно Google, IBM, Intel и Microsoft вложили около 0,5 млрд долларов в развитие квантовых компьютеров за последнее время, создали крупные лаборатории и исследовательские центры.

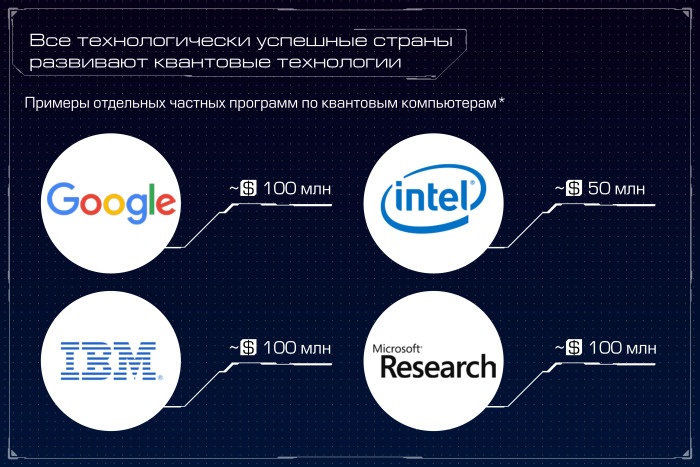
На Хабре и в Сети есть множество статей, например, вот, вот и вот, в которых текущее состояние дел с развитием квантовых технологий в разных странах рассматривается более подробно. Для нас сейчас главное, что все ведущие технологически развитые страны и игроки вкладывают огромные средства в исследования в этом направлении, что дает надежду на выход из текущего технологического тупика.

Направления развития

(к оглавлению)

На текущий момент (могу ошибаться, поправьте) основные усилия (и более-менее значимые результаты) у всех ведущих игроков сосредоточены на двух направлениях:

• Специализированные квантовые компьютеры, которые направлены на решение одной конкретной специфической задачи, например, задачи оптимизации. Примером продукта являются квантовые компьютеры D-Wave.
• Универсальные квантовые компьютеры — которые способны реализовать произвольные квантовые алгоритмы (Шора, Гровера, и т.д.). Реализации от IBM, Google.

 

Прочие же вектора развития, которые дает нам квантовая физика, такие как:

• квантовые сенсоры
• квантовая сеть как основа для квантовой криптографии
• и многое другое

 

безусловно тоже в списке направлений для исследований, но каких-то более-менее значимых результатов в настоящее время вроде как еще нет.

Дополнительно можно почитать дорожную карту развития квантовых технологий, ну и гуглите “развитие квантовых технологий”, например, вот, вот и вот.

Основы. Квантовый объект и квантовые системы

(к оглавлению)

Самое главное, что надо понять из этого раздела, это то, что

Квантовый компьютер (в отличие от обычного) в качестве носителей информации использует квантовые объекты, а для проведения вычислений квантовые объекты должны быть соединены в квантовую систему.

Что же такое квантовый объект?

Квантовый объект — объект микромира (квантового мира), который проявляет квантовые свойства:
 

• Имеет определенное состояние с двумя граничными уровнями
• Находится в суперпозиции своего состояния до момента измерения
• Запутывается с другими объектами для создания квантовых систем
• Выполняет теорему о запрете клонирования (нельзя скопировать состояние объекта)

Разберем каждое свойство более подробно:

Имеет определенное состояние с двумя граничными уровнями (конечное состояние)

Классический пример из реального мира — монета. У нее есть состояние “сторона”, которая принимает два граничных уровня — “орел” и “решка”.

Находится в суперпозиции своего состояния до момента измерения

Подбросили монетку, она летит и вращается. Пока она вращается невозможно сказать в каком из граничных уровней находится ее состояние “сторона”. Но стоит нам ее прихлопнуть и посмотреть на результат — как суперпозиция состояний тут же схлопывается в одно из двух граничных — “орел” и “решка”. Прихлопывание монетки в нашем случае и есть измерение.

Запутывается с другими объектами для создания квантовых систем

С монеткой сложно, но попробуем. Представьте мы подбросили три монетки так, что они вращаются цепляясь друг за друга, такое жонглирование монетками. В каждый момент времени не только каждая из них находится в суперпозиции состояний, но эти состояния взаимно влияют друг на друга (монетки же сталкиваются).

Выполняет теорему о запрете клонирования (нельзя скопировать состояние объекта)

Пока монетки летят и вращаются, мы никаким образом не можем создать отдельную от системы копию вращающегося состояния любой из монеток. Система живет сама в себе и очень ревностно относится к тому, чтобы выдать наружу какую-либо информацию.

Еще пара слов о самом понятии “суперпозиции”, практически во всех статьях суперпозицию объясняют как “находится во всех состояниях одновременно”, что, конечно, верно, но временами излишне запутывает. Суперпозицию состояний можно представить себе также как то, что в каждый момент времени у квантового объекта есть определенные вероятности схлопнуться в каждый из своих граничных уровней, и в сумме эти вероятности, естественно, равны 1. Далее при рассмотрении кубита мы остановимся на этом более подробно.

Для монеток это можно себе представить визуально — в зависимости от начальной скорости, угла подброса, состояния окружающей среды, в которой летит монетка, в каждый момент времени вероятность получить “орел” или “решку” разная. И, как говорилось ранее, состояние такой летящей монетки можно себе представить как “находится во всех своих граничных состояниях одновременно, но с разной вероятностью их реализации”.

Любой объект, для которого выполняются вышеуказанные свойства и который мы можем создать и управлять, может использоваться как носитель информации в квантовом компьютере.

Чуть дальше мы поговорим о текущем состоянии дел с физической реализацией кубитов как квантовых объектов, и что сейчас ученые используют в этом качестве.

Итак, третье свойство гласит, что квантовые объекты могут запутываться для создания квантовых систем. Что же такое квантовая система?

Квантовая система — система запутанных квантовых объектов, обладающая следующими свойствами:
 

• Квантовая система находится в суперпозиции всех возможных состояний объектов, из которых она состоит
• Нельзя узнать состояние системы до момента измерения
• В момент измерения система реализует один из возможных вариантов своих граничных состояний

(и, забегая чуть вперед)

Следствие для квантовых программ:
 

• Квантовая программа имеет заданное состояние системы на входе, суперпозицию внутри, суперпозицию на выходе
• На выходе программы после измерения имеем вероятностную реализацию одного из возможных конечных состояний системы (плюс возможные ошибки)
• Любая квантовая программа имеет архитектуру дымоходной трубы (вход -> выход. Нет циклов, нельзя посмотреть состояние системы в середине процесса.)

 

Сравнение квантового компьютера и обычного

(к оглавлению)

Давайте теперь сравним обычный компьютер и квантовый.

	Обычный компьютер	Квантовый компьютер
Логика	0 / 1	`a|0> + b|1>, a^2+b^2=1`
Физика	Полупроводниковый транзистор	Квантовый объект
Носитель инф.	Уровни напряжения	Поляризация, спин,…
Операции	NOT, AND, OR, XOR над битами	Вентили: CNOT, Адамара,…
Взаимосвязь	Полупроводниковый чип	Запутанность между собой
Алгоритмы	Стандартные (см. Кнут)	Специальные (Шор, Гровер)
Принцип	Цифровой, детерминированный	Аналоговый, вероятностный

Логический уровень

В обычном компьютере это бит. Хорошо нам знакомый насквозь детерминированный бит. Может принимать значения либо 0 либо 1. Он прекрасно справляется с ролью логической единицы для обычного компьютера, но совершенно не подходит для описания состояния квантового объекта, который, как мы уже говорили, в дикой природе находится в суперпозиции своих граничных состояний.

Для этого придумали кубит. В своих граничных состояниях он реализует похожие на 0 и 1 состояния |0> и |1>, а в суперпозиции представляет собой вероятностное распределение над своими граничными состояниями |0> и |1>:

 a|0> + b|1>, такое, что a^2+b^2=1

 

a и b при этом представляют собой амплитуды вероятностей, а квадраты их модулей — собственно вероятности получить именно такие значения граничных состояний |0> и |1>, если схлопнуть кубит измерением прямо сейчас.

Физический уровень

На текущем технологическом уровне развития физической реализацией бита для обычного компьютера выступает полупроводниковый транзистор, для квантового, как мы уже говорили, любой квантовый объект. В следующем разделе мы поговорим о том, что сейчас используется в качестве физических носителей кубитов.

Носитель информации

Для обычного компьютера это электрический ток — уровни напряжения, наличие или отсутствие тока, и т.д., для квантового — то самое состояние квантового объекта (направление поляризации, спин, и т.д.), которое может находится в состоянии суперпозиции.

Операции

Для реализации логических схем на обычном компьютере используются всем нам хорошо известные логические операции, для операций над кубитами пришлось придумывать совершенно иную систему операций, называемую квантовыми вентилями. Вентили бывают однокубитные и двухкубитные, в зависимости от того, над сколькими кубитами производится преобразование.

Примеры квантовых вентилей:

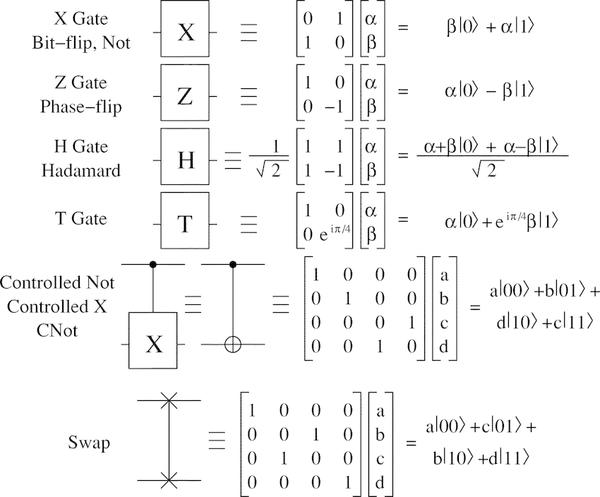
Есть понятие универсального набора вентилей, которых достаточно для выполнения любого квантового вычисления. Например, универсальным является набор, включающий вентиль Адамара, вентиль фазового сдвига, вентиль CNOT и вентиль ??8. С их помощью можно выполнить любое квантовое вычисление на произвольном наборе кубитов.

В этой статье мы не будем детально останавливаться на системе квантовых вентилей, более подробно про них и логические операции над кубитами можно почитать, например, вот тут. Главное, что надо запомнить:

• Операции над квантовыми объектами требуют создания новых логических операторов (квантовых вентилей)
• Квантовые вентили бывают однокубитные и двухкубитные
• Существуют универсальные наборы вентилей, с помощью которых можно выполнить любое квантовое вычисление

Взаимосвязь

Один транзистор нам совершенно бесполезен, чтобы производить вычисления нам надо соединить много транзисторов между собой, то есть создать полупроводниковый чип из миллионов транзисторов, на которых уже строить логические схемы, АЛУ и, в конечном счете, получить современный процессор в его классическом виде.

Один кубит нам тоже совершенно бесполезен (ну если только в академическом плане),

чтобы производить вычисления нам нужна система кубитов (квантовых объектов)

которая, как мы уже говорили, создается при помощи запутывания кубитов между собой так, чтобы изменения в их состояниях происходили согласованно.

Алгоритмы

Стандартные алгоритмы, которые накопило человечество к текущему моменту, совершенно не подходят для реализации на квантовом компьютере. Да в общем-то и незачем. Квантовые компьютеры, основанные на вентильной логике над кубитами, требуют создания совершенно иных алгоритмов, квантовых алгоритмов. Из наиболее известных квантовых алгоритмов можно выделить три:

• Алгоритм Шора (факторизация)
• Алгоритм Гровера (быстрый поиск в неупорядоченной базе данных)
• Алгоритм Дойча-Йожи (ответ на вопрос, постоянная или сбалансированная функция)

 

Принцип

И самое главное отличие — это принцип работы. У стандартного компьютера это цифровой, жестко детерминированный принцип, основанный на том, что если мы задали какое-то начальное состояние системы и пропустили его через заданный алгоритм, то результат вычислений будет один и тот же, сколько бы раз мы это вычисление не запускали. Собственно, такое поведение это именно то, что мы от компьютера и ждем.

Квантовый компьютер работает на аналоговом, вероятностном принципе. Результат работы заданного алгоритма на заданном начальном состоянии представляет собой выборку из вероятностного распределения конечных реализаций алгоритма плюс возможные ошибки.

Такая вероятностная природа квантовых вычислений обусловлена самой вероятностной сутью квантового мира. “Бог не играет в кости со вселенной”, — говорил старик Эйнштейн, но все эксперименты и наблюдения пока (в текущей научной парадигме) подтверждают обратное.

Физические реализации кубитов

(к оглавлению)

Как мы уже говорили, кубит может быть представлен квантовым объектом, то есть таким физическим объектом, который реализует описанные выше квантовые свойства. То есть грубо говоря, любой физический объект, в котором есть два состояния и эти два состояния находятся в состоянии суперпозиции можно использовать для построения квантового компьютера.

“Если мы умеем помещать атом в два разных уровня и управлять ими, то вот вам и кубит. Если мы можем это сделать с ионом, — кубит. С током то же самое. Если мы запускаем его по часовой стрелке и против часовой стрелки одновременно, вот вам кубит.” (С)

Есть прекрасный комментарий к статье, в котором текущее многообразие физических реализаций кубита рассматривается более подробно, мы же просто перечислим наиболее известные и распространенные:

• сверхпроводниковые кубиты
• зарядовые кубиты
• ионные ловушки
• квантовые точки
• и множество других экзотических идей (анионы и прочее)

 

Из всего этого многообразия наиболее проработанным является первый метод получения кубитов, основанный на сверхпроводниках. Google, IBM, Intel и прочие ведущие игроки используют именно его для построения своих систем.

Ну и еще почитайте обзор возможных физических реализаций кубитов от Andrew Daley,2014.

Основы. Принцип работы квантового компьютера

(к оглавлению)

Материалы для данного раздела (задача и картинки) взяты из статьи “Просто о сложном. Как работает квантовый компьютер”.

Итак, представим, что у нас есть следующая задача:

Есть группа из трех человек: (А)ндрей, (B)олодя и (С)ережа. Есть два такси (0 и 1).

Известно также, что :

• (А)ндрей, (B)олодя — друзья
• (А)ндрей, (С)ережа — враги
• (B)олодя и (С)ережа — враги

 

Задача: Разместить народ по такси так, чтобы Max(друзья) и Min(враги)

Оценка: L = (кол-во друзей) — (кол-во врагов) для каждого варианта размещения

ВАЖНО: Предположим, что эвристик нет, оптимального решения нет. В этом случае задача решается только полным перебором вариантов.

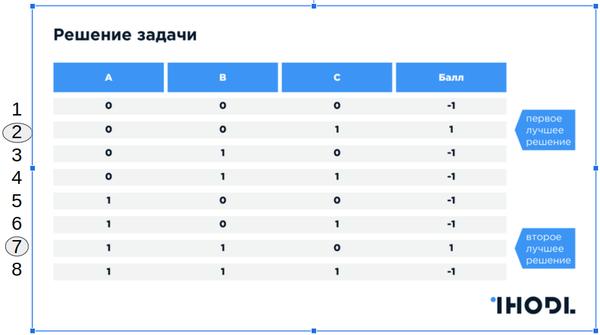
Решение на обычном компьютере

Как решать эту задачу на обычном (супер)компьютере (или кластере) — понятно, что надо перебрать в цикле все возможные варианты. Если у нас мультипроцессорная система, то можно распараллелить расчет решений на несколько процессоров и потом собрать результаты.

У нас 2 возможных варианта размещения (такси 0 и такси 1) и 3 человека. Пространство решений 2^3 = 8. Перебрать 8 вариантов можно даже на калькуляторе, это не проблема. А теперь усложним задачу — у нас 20 человек и два автобуса, пространство решений 2^20 = 1 048 576. Тоже ничего сложного. Увеличим количество людей в 2.5 раза — возьмем 50 человек и два поезда, пространство решений теперь 2^50 = 1.12 x 10^15. У обычного (супер)компьютера уже начинаются серьезные проблемы. Увеличим кол-во людей в 2 раза, 100 человек дадут нам уже 1.2 x 10^30 возможных вариантов.

Все, за разумное время эту задачу не посчитать.

Подключаем суперкомпьютер

Самый мощный компьютер в настоящее время — номер 1 из Top500, это Summit, производительностью 122 Пфлопс. Предположим, что на расчет одного варианта нам достаточно 100 операций, тогда для решения задачи для 100 человек нам потребуется:

(1.2 x 10^30 100) / 122x10^15 / (606024365) = 3 х 10^37 лет.

Как мы видим, при увеличении размерности исходных данных пространство решений растет по степенному закону, в общем случае для N битов у нас есть 2^N возможных вариантов решения, которые при сравнительно небольших N (100) дают нам непросчитываемое (на текущем технологическом уровне) пространство решений.

Есть ли альтернативы? Как вы уже догадались, таки да, есть.

Но прежде чем мы перейдем к тому, как и почему квантовые компьютеры позволяют эффективно решать подобные задачи, давайте немного вспомним о том, что такое вероятностное распределение. Не пугайтесь, статья обзорная, жесткой математики тут не будет, обойдемся классическим примером с мешком и шариками.

Совсем немного комбинаторики, теории вероятностей и странного экспериментатора

Возьмем мешок и положим в него 1000 белых и 1000 черных шаров. Будем проводить эксперимент — вынимать шар, записывать цвет, возвращать шар в мешок и перемешивать шары в мешке.

Провели эксперимент 10 раз, вытащили 10 черных шаров. Возможно? Вполне. Дает нам эта выборка какое-то разумное понятие об истинном распределение в мешке? Очевидно, что нет. Что надо сделать — правильно, повторить эксперимент миллион раз и рассчитать частоты выпадения черных и белых шаров. Получим, например 49.95% черных и 50.05% белых. В этом случае уже более-менее понятна структура распределения из которого мы семплируем (вынимаем один шарик).

Главное, что надо понять, что сам эксперимент имеет вероятностную природу, одним семплом (шариком) мы не узнаем истинную структуру распределения, нам надо многократно повторить эксперимент и усреднить результаты.

Добавим в наш мешок 10 красных и 10 зеленых шаров (ошибки). Повторим эксперимент 10 раз. Вытащили 5 красных и 5 зеленых. Возможно? Да. Можем что-то сказать об истинном распределении — Нет. Что надо сделать — ну вы поняли.

Для получения понимания о структуре вероятностного распределения надо многократно просемплировать единичные исходы из этого распределения и усреднить результаты.

 

Связываем теорию с практикой

Теперь вместо черных и белых шаров давайте возьмём бильярдные шары, и положим в мешок 1000 шаров с номером 2, 1000 с номером 7 и 10 шаров с другими номерами. Представим себе экспериментатора, который обучен простейшим действиям (достать шар, записать номер, положить шар обратно в мешок, перемешать шары в мешке) и делает он это за 150 микросекунд. Ну такой экспериментатор на спидах (не реклама наркотиков!!!). Тогда за 150 секунд он сможет провести наш эксперимент 1 миллион раз и предоставить нам результаты усреднения.

Усадили экспериментатора, дали мешок, отвернулись, подождали 150 секунд — получили:

номер 2 — 49.5%, номер 7 — 49.5%, остальные номера в сумме — 1%.

Да, все верно, наш мешок — это квантовый компьютер с алгоритмом, решающим нашу задачу, а шары — возможные варианты решения. Поскольку правильных решений два, то квантовый компьютер будет выдавать нам равновероятно любое из этих возможных решений, и 0.5% (10/2000) ошибок, о которых мы поговорим позднее.

Для получения результата работы квантового компьютера надо многократно запустить квантовый алгоритм на одном и том же входном наборе данных и усреднить результат.

 

Масштабируемость квантового компьютера

Теперь представим себе, что для задачи, в которой участвуют 100 человек (пространство решений 2^100 мы помним об этом), правильных решений тоже только два. Тогда, если взять 100 кубитов и написать алгоритм, вычисляющий нашу целевую функцию (L, см. выше) над этими кубитами, то мы получим мешок, в котором будет 1000 шаров с номером первого правильного ответа, 1000 с номером второго правильного ответа и 10 шаров с другими номерами. И наш экспериментатор за те же 150 секунд выдаст нам оценку вероятностного распределения правильных ответов.

Время выполнения квантового алгоритма (с некоторыми допущениями) можно считать константным О(1) по отношению к размерности пространства решений (2^N).

И вот именно это свойство квантового компьютера — константность времени выполнения по отношению к возрастающей по степенному закону сложности пространства решений и является ключевым.

Кубит и параллельные миры

Как же это происходит? Что позволяет квантовому компьютеру так быстро производить расчеты? Все дело в квантовой природе кубита.

Смотрите, мы говорили, что кубит как квантовый объект реализует одно из двух своих состояний при его наблюдении, но в “живой природе” находится в суперпозиции состояний, то есть находится в обоих своих граничных состояниях одновременно (с некоторой вероятностью).

Возьмем (А)ндрея и представим его состояние (в каком он транспортном средстве — 0 или 1) как кубит. Тогда у нас возникает (в квантовом пространстве) два параллельных мира, в одном (А) сидит в такси 0, в другом мире — в такси 1. Одновременно в двух такси, но с некоторой вероятность найти его в каждом из них при наблюдении.

Возьмем (В)олодю и тоже представим его состояние как кубит. Возникает два других параллельных мира. Но пока эти пары миров (А) и (В) никак не взаимодействуют. Что надо сделать, чтобы создать связанную систему? Правильно, надо эти кубиты связать (запутать). Берем и запутываем (А) с (В) — получаем квантовую систему из двух кубитов (А, В), реализующую внутри себя четыре взаимозависимых параллельных мира. Добавляем (С)ергея и получаем систему из трех кубитов (АВС), реализующую восемь взаимозависимых параллельных миров.

Сутью квантовых вычислений (реализации цепочки квантовых вентилей над системой связанных кубитов) является тот факт, что вычисление происходит во всех параллельных мирах одновременно.

И неважно сколько их у нас, 2^3 или 2^100, квантовый алгоритм выполнится за конечное время над всеми этими параллельными мирами и выдаст нам результат, представляющий собой семпл из вероятностного распределения ответов алгоритма.

Для лучшего понимания можно себе представить, что квантовый компьютер на квантовом уровне запускает 2^N параллельных процессов решения, каждый из которых работает над одним возможным вариантом, потом собирает результаты работы — и выдает нам ответ в виде суперпозиции решения (вероятностного распределения ответов), из которого мы каждый раз (при каждом эксперименте ) семплируем одно.

Запомните время, необходимое нашему экспериментатору (150 мкс) для проведения эксперимента, это пригодится нам чуть дальше, когда мы будем говорить об основных проблемах квантовых компьютеров и о времени декогеренции.

Квантовые алгоритмы

(к оглавлению)

Как уже говорилось, обычные алгоритмы, основанные на бинарной логике, неприменимы к квантовому компьютеру, использующему квантовую логику (квантовые вентили). Для него пришлось придумывать новые, в полной мере использующие потенциал, заложенный в квантовую природу вычислений.

Наиболее известные на сегодняшний день алгоритмы это:

• Алгоритм Шора
• Алгоритм Гровера
• Алгоритм Дойча — Йожи

 

В отличие от классических, квантовые компьютеры не универсальны.
До сих пор найдено лишь небольшое число квантовых алгоритмов.(С)

Спасибо oxoron за ссылку на Quantum Algorithm Zoo, место, где, по уверениям автора ("Stephen Jordan"), собраны и продолжают собираться лучшие представители квантово-алгоритмического мира.

В данной статье мы не будем подробно разбирать квантовые алгоритмы, в Сети много прекрасных материалов на любой уровень сложности, но кратко пробежаться по трем самым известным все-таки надо.

Алгоритм Шора.

(к оглавлению)

Наиболее известным квантовым алгоритмом является алгоритм Шора (придумал в 1994 году английский математик Питер Шор), который нацелен на решение задачи разложения чисел на простые множители (задача факторизации, дискретного логарифма).

Именно этот алгоритм приводят в пример, когда пишут о том, что ваши банковские системы и пароли скоро будут взломаны. Учитывая, что длина используемых на сегодняшний день ключей не менее чем 2048 бит, время для шапочки еще не пришло.

На сегодняшний день результаты более чем скромные. Лучшие результаты факторизации с помощью алгоритма Шора — числа 15 и 21, что сильно меньше, чем 2048 бит. Для остальных результатов из таблицы применялся иной алгоритм расчетов, но даже лучший по этому алгоритму результат (291311) сильно далек от реального применения.

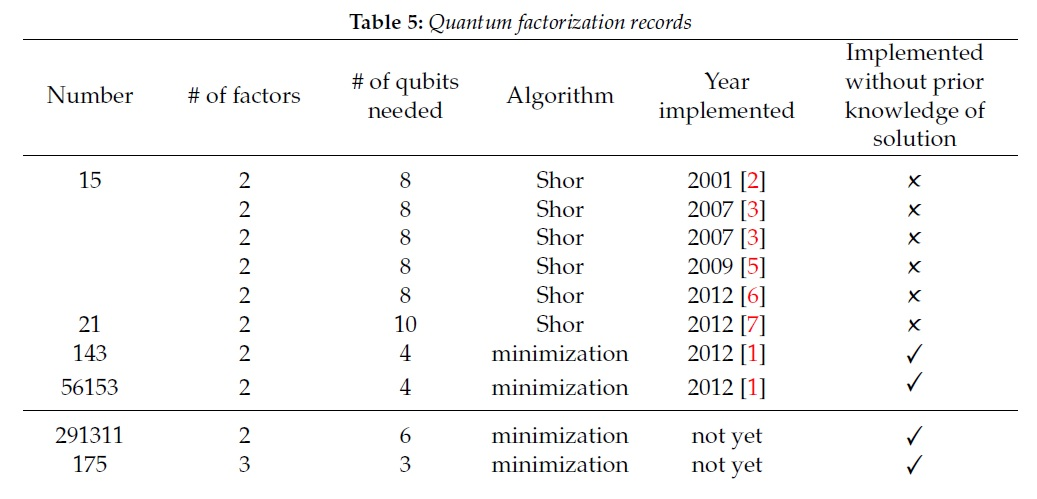
Подробнее про алгоритм Шора можно почитать, например, вот тут. Про практическую реализацию — тут.

Одна из текущих оценок сложности и необходимой мощности для факторизации числа из 2048 бит это компьютер с 20 миллионами кубитов. Спим спокойно.

Алгоритм Гровера

(к оглавлению)

Алгоритм Гровера — квантовый алгоритм решения задачи перебора, то есть нахождения решения уравнения F(X) = 1, где F — есть булева функция от n переменных. Был предложен американским математиком Ловом Гровером в 1996 году.

Алгоритм Гровера может быть использован для нахождения медианы и среднего арифметического числового ряда. Кроме того, он может применяться для решения NP-полных задач путем исчерпывающего поиска среди множества возможных решений. Это может повлечь значительный прирост скорости по сравнению с классическими алгоритмами, хотя и не предоставляя «полиномиального решения» в общем виде.(С)

Подробнее можно почитать вот тут, или тут. Еще вот тут есть хорошее объяснение алгоритма на примере ящиков и мяча, но, к сожалению, по независящим ни от кого причинам, данный сайт у меня из России не открывается. Если у вас этот сайт тоже заблокирован, то вот краткая выжимка:

Алгоритм Гровера. Представьте, что у вас имеется N штук пронумерованных закрытых коробок. Они все пустые кроме одной, в которой находится мячик. Ваша задача: узнать номер коробки, в которой находится мячик (этот неизвестный номер часто обозначают буквой w).

Как решать эту задачу? Самым тупым способом, по очереди открывать коробки, и рано или поздно вы наткнетесь на коробку с мячиком. А сколько в среднем коробок нужно проверить до того, как будет обнаружена коробка с мячиком? В среднем нужно открыть примерно половину коробок N/2. Главное здесь то, что если мы увеличим число коробок в 100 раз, то в те же 100 раз увеличится и среднее число коробок, которые нужно открыть до того, как будет найдена коробка с мячиком.

Теперь сделаем ещё одно уточнение. Пусть мы не сами открываем коробки руками и проверяем наличие мячика в каждой, а имеется некий посредник, назовем его Оракул (Oracle). Мы говорим Оракулу — «проверь коробку номер 732», и Оракул честно проверяет и отвечает «в коробке номер 732 мячика нет». Теперь вместо слов о том, сколько коробок нам нужно в среднем открыть, мы говорим «сколько раз в среднем мы должны обратиться к Оракулу для того, чтобы найти номер коробки с мячиком»

Оказывается, что если перевести эту задачу с коробками, мячиком и Оракулом на квантовый язык, то выходит замечательный результат: для поиска номера коробки с мячиком среди N коробок нам нужно потревожить Оракула всего примерно SQRT(N) раз!

То есть сложность задачи перебора используя алгоритм Гровера снижается в квадратный корень раз.

Алгоритм Дойча-Йожи

(к оглавлению)

Алгоритм Дойча — Йожи (упоминается также как алгоритм Дойча — Джозы) — [квантовый алгоритм](https://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%BD%D1%82%D0%BE%D0%B2%D1%8B%D0%B9%D0%B0%D0%BB%D0%B3%D0%BE%D1%80%D0%B8%D1%82%D0%BC), предложенный Давидом Дойчем и Ричардом Йожей в 1992 году, и ставший одним из первых примеров алгоритмов, предназначенных для выполнения на квантовых компьютерах. _

Задача Дойча — Йожи заключается в определении, является ли функция нескольких двоичных переменных F(x1, x2, … xn) постоянной (принимает либо значение 0, либо 1 при любых аргументах) или сбалансированной (для половины области определения принимает значение 0, для другой половины 1). При этом считается априорно известным, что функция либо является константой, либо сбалансирована. (С)

Еще можно почитать тут. Более простое объяснение:

Алгоритм Дойча (Дойча — Йожи) основан на переборе, но позволяет делать его быстрее обычного. Представьте, что на столе лежит монета и необходимо узнать фальшивая ли она или нет. Для этого нужно дважды посмотреть на монету и определить: «орел» и «решка» – настоящая, два «орла», две «решки» — фальшивая. Так вот, если использовать квантовый алгоритм Дойча, то это определение можно сделать одним взглядом – измерением. (С)

Проблемы квантовых компьютеров

(к оглавлению)

При проектировании и эксплуатации квантовых компьютеров перед учеными и инженерами возникает огромное количество проблем, которые на сегодняшний день решаются с переменным успехом. Согласно исследованию (и еще вот тут) можно выделить следующий ряд проблем:

• Чувствительность к окружению и взаимодействию с окружением
• Накопление ошибок при вычислениях
• Сложности с начальной инициализации состояний кубитов
• Сложности с созданием многокубитных систем

 

Крайне рекомендую прочитать статью “Характеристики квантовых компьютеров”, особенно комментарии к ней.

Давайте организуем все основные проблемы в три большие группы и рассмотрим поподробнее каждую из них:

Декогеренция

(к оглавлению)

Описание от N+1.

Квантовое состояние очень хрупкая штука, кубиты в запутанном состоянии крайне нестабильны, любое внешнее воздействие может разрушить (и разрушает) эту связь. Изменение температуры на мельчайшую долю градуса, давление, пролетевший рядом случайный фотон — все это дестабилизирует нашу систему.

Для решения этой проблемы строят низкотемпературные саркофаги, в которых температура (-273.14 градуса цельсия) чуть-чуть выше абсолютного ноля, с максимальной изоляцией внутренней камеры с процессором от всех (возможных) воздействий внешней среды.

Максимальное время жизни квантовой системы из нескольких запутанных кубитов, в течение которого она сохраняет свои квантовые свойства и может быть использована для произведения вычислений, называют временем декогеренции.

На текущий момент время декогеренции в лучших квантовых решениях составляет порядка десятков и сотен микросекунд.

Есть прекрасный сайт, на котором можно посмотреть сравнительные таблицы параметров всех созданных квантовых систем. В эту статью для примера вынесены только два топовых процессора — от IBM IBM Q System One и от Google Sycamore. Как мы видим, время декогеренции (Т2) не превышает 200 мкс.

Я не нашел точных данных по Sycamore, но в самой статье о квантовом превосходстве приводятся две цифры — 1 миллион вычислений за 200 секунд, в другом месте — за 130 секунд без потерь на управляющие сигналы и прочее. В любом случае это дает нам время декогеренции порядка 150 мкс. Помните нашего экспериментатора с мешком? Ну так вот он.

Computer Name	N Qubits	Max paired	T2 (мкс)
IBM Q System One	20	6	70
Google Sycamore	53	4	~150-200

Чем нам грозит декогеренция?

Основная проблема в том, что через 150 мкс наша вычислительная система из N запутанных кубитов начнет выдавать на выходе вместо вероятностного распределения правильных решений — вероятностный белый шум.

То есть нам надо:

• Инициализировать систему кубитов
• Провести вычисление (цепочка вентильных операций)
• Считать результат

 

И сделать все это за 150 мкс. Не успел — результат превратился в тыкву.

Но это еще не все...

Ошибки

(к оглавлению)

Как мы уже говорили, квантовые процессы и квантовые вычисления имеют вероятностную природу, мы не можем быть уверены на 100% ни в чем, а только с какой-то вероятностью. Ситуация усугубляется еще и тем, что квантовые вычисления подвержены ошибкам. Основные типы ошибок при квантовых вычислениях это:

• Ошибки декогеренции, обусловлены сложностью системы и взаимодействием с внешней средой
• Вычислительные ошибки гейтов (обусловлены квантовой природой вычислений)
• Ошибки считывания финального состояния (результата)

 

Ошибки, связанные с декогерентностью, возникают сразу же, как только мы запутали наши кубиты и начали производить вычисления. Чем больше кубитов мы запутали, тем сложнее система, и тем легче ее разрушить. Низкотемпературные саркофаги, защищенные камеры, все эти технологические ухищрения как раз направлены на то, чтобы снизить число ошибок и продлить время декогеренции.

Вычислительные ошибки гейтов — любая операция (вентиль) над кубитами может с некоторой вероятностью завершиться с ошибкой, а нам для реализации алгоритма нужно выполнить сотни вентилей, вот и представьте, что мы получим в конце выполнения нашего алгоритма. Классический вариант ответа на вопрос — “Какова вероятность встретить динозавра в лифте?” — 50х50, или встретишь или нет.

Проблема еще усугубляется тем, что стандартные методы коррекции ошибок (дублирование вычислений и усреднение) в квантовом мире не работают из-за теоремы о запрете клонирования. Для коррекции ошибок в квантовых вычислениях пришлось придумать квантовые же методы коррекции. Грубо говоря мы берем N обычных кубитов и делаем из них 1 логический кубит с меньшим уровнем ошибок.

Но тут возникает другая проблема — общее количество кубитов. Смотрите, допустим у нас есть процессор со 100 кубитами, из которых 80 кубитов заняты коррекцией ошибок, тогда нам для вычислений остается только 20.

Ошибки считывания финального результата — как мы помним, результат квантовых вычислений нам представлен в виде вероятностного распределения ответов. Но считывание финального состояния тоже может завершиться с ошибкой.

На том же сайте есть сравнительные таблицы процессоров по уровням ошибок. Для сравнения возьмем те же процессоры, что и в предыдущем примере — IBM IBM Q System One и Google Sycamore:

Computer	1-Qubit Gate Fidelity	2-Qubit Gate Fidelity	Readout Fidelity
IBM Q System One	99.96%	98.31%	—
Google Sycamore	99.84%	99.38%	96.2%

Здесь фиделити — мера схожести двух квантовых состояний. Величину ошибки можно грубо представить как 1-Fidelity. Как мы видим, ошибки на 2-х кубитных гейтах и ошибки считывания являются главным препятствием к выполнению сложных и длинных алгоритмов на существующих квантовых компьютерах.

Еще можно почитать роадмап от 2016 года от NQIT по решению задачи коррекции ошибок.

Архитектура процессора

(к оглавлению)

В теории мы строим и оперируем схемами из десятков запутанных кубитов, в реальности же все сложнее. Все существующие квантовые чипы (процессоры) построены таким образом, что обеспечивают безболезненное запутывание одного кубита только со своими соседями, которых не больше шести.

Если же нам надо запутать 1-й кубит, скажем, с 12-м, то нам придется строить цепочку дополнительных квантовых операций, задействовать дополнительные кубиты и прочее, что увеличивает общий уровень ошибок. Да, и не забывайте про время декогеренции, возможно к тому моменту, когда вы закончите связывать кубиты в нужную вам схему, время закончится и вся схема превратится в симпатичный генератор белого шума.

Также не забывайте, что архитектура у всех квантовых процессоров разная, и программу, написанную в эмуляторе в режиме “связность всех со всеми” нужно будет “перекомпилировать” в архитектуру конкретного чипа. Есть даже специальные программы оптимизаторы для выполнения этой операции.

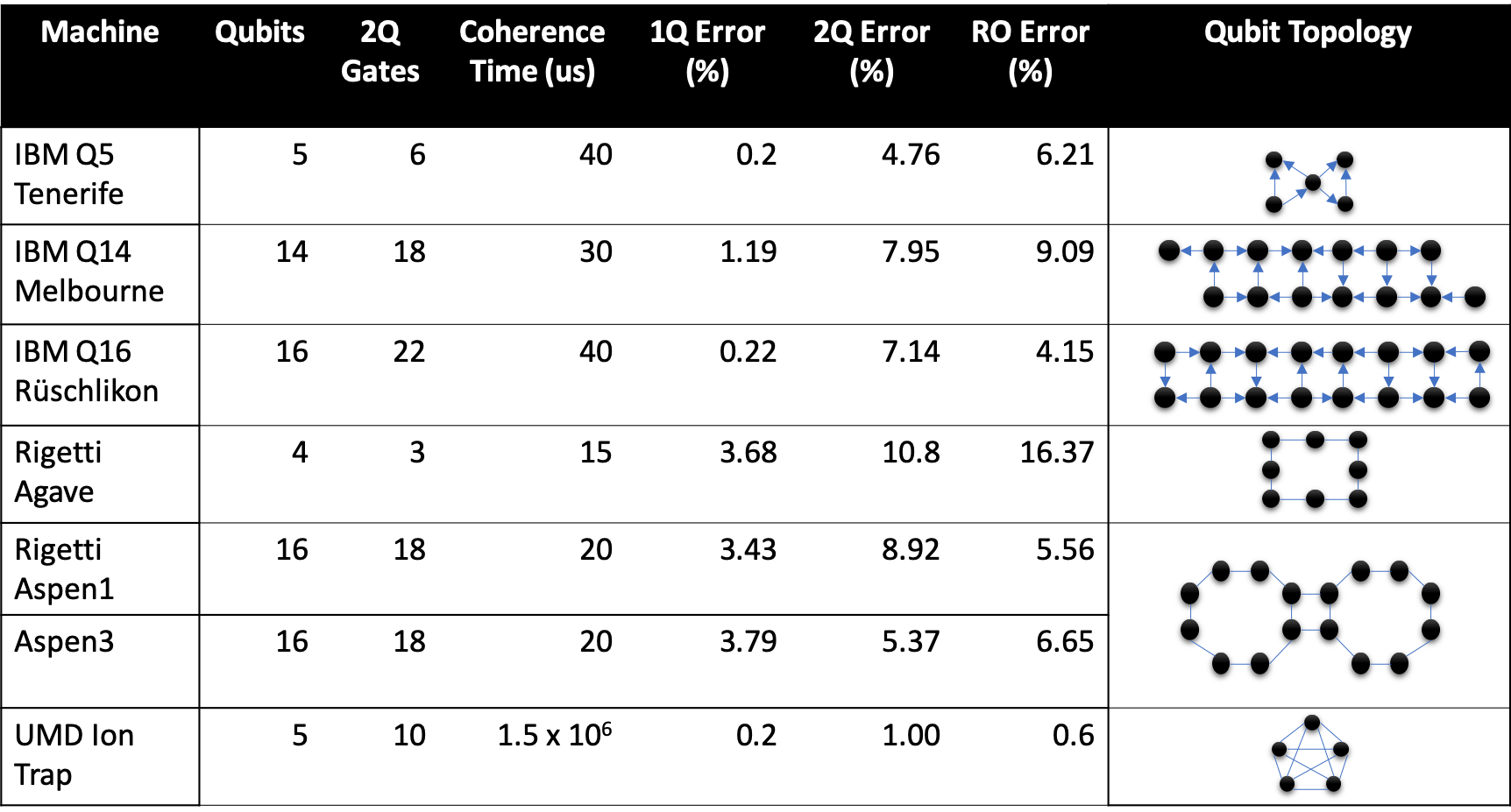
Максимальная связность и максимальное количество кубитов для тех же топовых чипов:

Computer Name	N Qubits	Max paired	T2 (мкс)
IBM Q System One	20	6	70
Google Sycamore	53	4	~150-200

И, для сравнения, таблица с данными предыдущего поколения процессоров. Сравните количество кубитов, время декогеренции и процент ошибок с тем, что мы имеем сейчас у нового поколения. Все-таки прогресс потихоньку, но движется.

Итак:

• На текущий момент нет полносвязных архитектурных схем из > 6 кубитов
• Чтобы на реальном процессоре запутать кубит 0 с, например, 15-м может потребоваться несколько десятков дополнительных операций
• Больше операций -> больше ошибок -> сильнее влияние декогерентности

 

Итоги

(к оглавлению)

Декогеренция — прокрустово ложе современных квантовых вычислений. В 150 мкс мы должны уложить все:

• Инициализацию начального состояния кубитов
• Вычисление задачи с использованием квантовых гейтов
• Провести коррекцию ошибок, чтобы получить значимый результат
• Считать полученный результат

 

Пока результаты неутешительные, хотя вот тут заявляют о достижении 0.5с времени удержания когерентности на квантовом компьютере, основанном на ионных ловушках:

We measure a qubit coherence time in excess of 0.5 s, and with magnetic shielding we expect this to improve to be longer than 1000 s

Про эту технологию еще можно почитать здесь или, например, здесь.

Ситуация осложняется еще и тем, что при совершении сложных вычислений необходимо использовать квантовые схемы коррекции ошибок, что тоже отъедает и время, и доступные кубиты.

Ну и, наконец, современные архитектуры не позволяют с минимальными затратами реализовать схемы запутанности лучше, чем 1 к 4 или 1 к 6.

Пути решения проблем

(к оглавлению)

Для решения вышеуказанных проблем, в настоящее время используют следующие подходы и методы:

• Использование криокамер с низкими температурами (10 мК (–273,14°C))
• Использование максимально защищенных от внешних воздействий процессорных блоков
• Использование систем квантовой коррекции ошибок (Логический кубит)
• Использование оптимизаторов при программировании схем для конкретного процессора

 

Также проводятся исследования, направленные на увеличение времени декогеренции, на поиск новых (и доработку известных) физических реализаций квантовых объектов, на оптимизацию схем коррекции и прочее и прочее. Прогресс есть (посмотрите выше на характеристики более ранних и топовых на сегодняшний день чипов), но пока идет медленно, очень очень медленно.

D-Wave

(к оглавлению)

2000-кубитный компьютер D-Wave 2000Q. Источник: D-Wave Systems

На фоне заявления Google о достижении квантового превосходства используя процессор с 53-мя кубитами, компьютеры и анонсы от компании D-Wave, в которых число кубитов исчисляется тысячами, несколько сбивает с толку. Ну действительно, если 53 кубита смогли достичь квантового превосходства, то на что же способен компьютер с 2048 кубитами? Но не все так хорошо...

Если коротко (взято из вики):

Компьютеры D-Wave работают на принципе квантовой релаксации (квантовый отжиг), могут решать крайне ограниченный подкласс задач оптимизации, и не подходят для реализации традиционных квантовых алгоритмов и квантовых вентилей.

Более подробно можно почитать, например, тут, тут (осторожно, может не открываться из России), или у Scott Aaronson в статье из его блога. Кстати, очень рекомендую почитать вообще его блог, там много хорошего материала

Вообще с самого начала анонсов у научного сообщества возникали вопросы к компьютерам D-Wave. Например, в 2014 году IBM поставила под сомнение факт, что D-Wave использует квантовые эффекты. Дело дошло до того, что в 2015 году Google вместе с NASA купила один из таких квантовых компьютеров и после исследований подтвердила, что таки да, компьютер работает и вычисляет задачу быстрее, чем обычный. Еще про заявление Google можно почитать тут и, например, тут.

Главное, что компьютеры D-Wave, с их сотнями и тысячами кубитов нельзя использовать для вычисления и запуска квантовых алгоритмов. На них нельзя запустить алгоритм Шора, например. Все, что они могут — это используя определенные квантовые механизмы решать определенную задачу оптимизации. Можно считать, что D-Wave это такой квантовый ASIC для конкретной задачи.

 

Немного об эмуляции квантовых компьютеров

(к оглавлению)

Квантовые вычисления можно эмулировать на обычном компьютере. Ведь действительно, смотрите:

• Состояние кубита можно представить комплексным числом, занимающим от 2х32 до 2х64 бита (8-16 байт) в зависимости от архитектуры процессора
• Состояние N связанных кубитов можно представить в виде 2^N комплексных чисел, т.е. 2^(3+N) для 32-х битной архитектуры и 2^(4+N) для 64-х битной.
• Квантовую операцию над N кубитами можно представить матрицей 2^N x 2^N

 

Тогда:

• Для хранения эмулируемых состояний 10 кубитов нужны 8 КБ
• Для хранения состояний 20 кубитов нужны 8 МБ
• Для хранения состояний 30 кубитов нужны 8 ГБ
• Для хранения состояний 40 кубитов нужны 8 Терабайт
• Для хранения состояний 50 кубитов нужны 8 Петабайт и т.д.

 

(С)

Для сравнения, Summit (Top-1 из Top-500) несет на себе всего 2.8 Петабайт памяти.

Текущий рекорд симуляций — 49 кубит поставленный в прошлом году на крупнейшем китайском суперкомпьютере (Sunway Taihu Light)

Предел симуляции квантового компьютера на классических системах обусловлен количеством оперативной памяти необходимой для хранения состояния кубитов.

Рекомендую еще прочитать вот этот комментарий. Оттуда:

По операциям — для точной эмуляции схемы на 49 кубитов из каких-то 39 "тактов" (независимых слоев вентилей) потребовалось 2^63 комплексных умножений — 4 Пфлопс суперкомпьютера на протяжении 4 часов

Эмуляция квантового компьютера из 50+ кубит на классических системах считается невыполнимой за разумное время. В том числе из-за этого факта Google использовал для своего эксперимента с квантовым превосходством процессор с 53-мя кубитами.

 

Квантовое вычислительное превосходство.

(к оглавлению)

Википедия дает нам следующее определение квантового вычислительного превосходства:

Ква?нтовое превосхо?дство — способность квантовых вычислительных устройств решать проблемы, которые классические компьютеры практически не могут решить.

Фактически достижение квантового превосходства означает, что, например, факторизацию больших чисел по алогритму Шора можно решать за адекватное время, или можно эмулировать на квантовом уровне сложные химические молекулы, и так далее. То есть новая эпоха наступила.

Но в формулировке определения есть некоторая лазейка, “которые классические компьютеры практически не могут решить”. Фактически это означает, что если создать квантовый компьютер из 50+ кубитов и запустить на нем некоторую квантовую схему, то, как мы рассматривали выше, результат работы этой схемы невозможно будет сэмулировать на обычном компьютере. То есть классический компьютер воссоздать результат работы такой схемы будет не в состоянии.

Является ли такой результат реальным квантовым превосходством или нет, вопрос скорее философский. Но понимать, что сделал Google, и на чем основано его недавнее заявление о достижении квантового превосходства на своем новом процессоре Sycamore надо.

Заявление Google о достижении квантового превосходства

(к оглавлению)

54-кубитный процессор Sycamore

Итак, в октябре 2019 года разработчики Google опубликовали в научном издании Nature статью «Квантовое превосходство с применением программируемого сверхпроводящего процессора». Авторы объявили о достижении впервые в истории квантового превосходства с помощью 54-кубитного процессора «Sycamore».

В сети в статьях Sycamore часто упоминают то как 54-х кубитный процессор, то как 53-х. Истина в том, что согласно оригинальной статье, процессор физически состоит из 54-х кубитов, но один из них нерабочий и выведен из эксплуатации. Таким образом, в реальности мы имеем 53-х кубитный процессор.

В Сети тут же появилось множество материалов на эту тему, градус которых варьировался от восторженных до скептических.

Позднее сотрудники отдела квантовых вычислений компании IBM заявили, что Google ложно сообщила о достижении квантового превосходства. В компании утверждают, что обычный вычислитель справится с этой задачей в худшем случае за 2,5 дня, и при этом полученный ответ будет точнее, чем у квантового компьютера. Такой вывод был сделан по итогам проведенного теоретического анализа нескольких способов оптимизации.

Ну и, конечно, Scott Aaronson в своем блоге не смог обойти своим вниманием это заявление. Его анализ вместе со всеми ссылками и Scott’s Supreme Quantum Supremacy FAQ! как обычно стоят того, чтобы потратить на них свое время. На хабре есть перевод этого FAQ, и обязательно почитайте комментарии, там есть ссылки на предварительные документы, утекшие в Сеть до официального объявления.

Что же в реальности сделал Google? Для детального понимания почитайте Ааронсона, а кратко вот:

Я могу, конечно, вам сказать, но чувствую себя при этом глуповато. Вычисление такое: экспериментатор генерирует случайную квантовую схему С (т.е. Случайную последовательность 1-кубитных и 2-кубитных — между ближайшими соседями — вентилей, с глубиной к примеру в 20, действующую на 2D сеть n=50-60 кубитов). После этого экспериментатор посылает С на квантовый компьютер, и просит его применить С к начальному состоянию из 0, измерить результат в базисе {0,1}, послать обратно n-битную наблюдаемую последовательность (строку) и повторить несколько тысяч или миллионов раз. Наконец, используя свое знание о С, экспериментатор проводит статистическую проверку на соответствие результата с ожидаемым выходом от квантового компьютера.

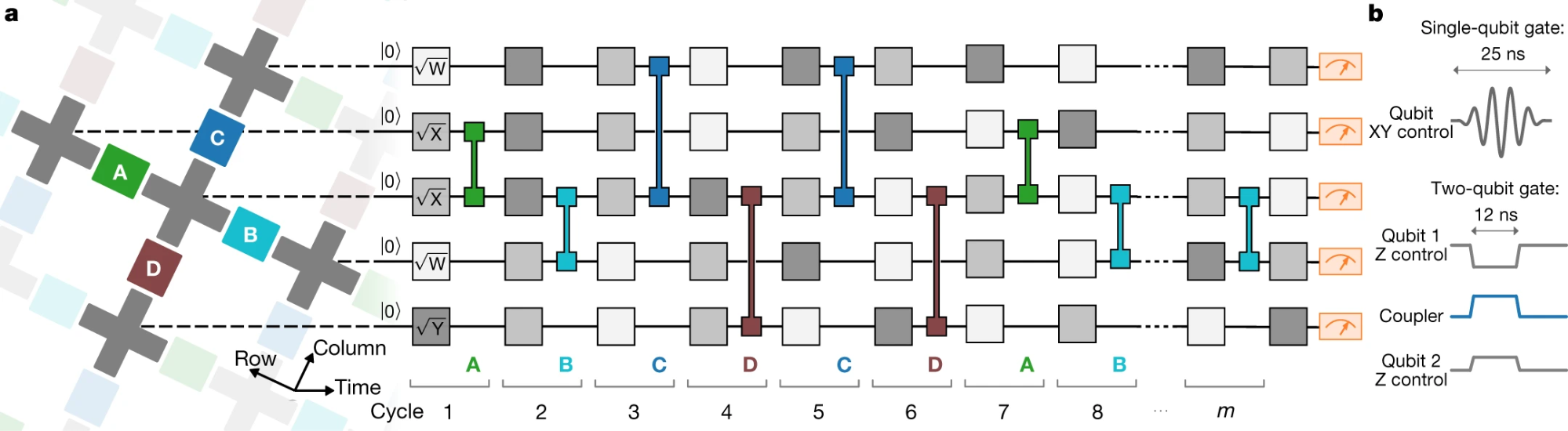
Совсем коротко:

• Создается случайная схема длиной 20 из 53 кубитов используя вентили
• Схема запускается с начальным состоянием [0...0] на выполнение
• Выход схемы представляет собой случайную битовую строку (семпл)
• Распределение результата не является случайным (интерференция)
• Распределение полученных семплов сравнивается с ожидаемым
• Делается вывод о квантовом превосходстве

 

То есть Google реализовал синтетическую задачу на 53-х кубитном процессоре, и свое заявление о достижении квантового превосходства основывает на факте невозможности эмуляции такого процессора на стандартных системах за разумное время.

Для понимания — в этом разделе нисколько не умаляется достижение Google, инженеры действительно молодцы, а вопрос о том можно считать это реальным квантовым превосходством или нет, как уже говорилось ранее, скорее философский, чем инженерный. Но надо понимать, что достигнув такого вычислительного превосходства мы ни на шаг не продвинулись к возможности запускать алгоритм Шора на 2048-и битных числах.

Резюме

(к оглавлению)

Квантовые компьютеры и квантовые вычисления — очень многообещающая, очень молодая и пока малоприменимая в промышленном плане область информационных технологий.

 

Развитие квантовых вычислений позволит (когда-нибудь) решать задачи:

• Моделирования сложных физических систем на квантовом уровне
• Нерешаемые на обычном компьютере из-за вычислительной сложности

 

Основные проблемы при создании и эксплуатации квантовых компьютеров:

• Декогеренция
• Ошибки (декогеренции и вентильные)
• Архитектура процессоров (полносвязные схемы кубитов)

 

Состояние дел на текущий момент:

• По факту — самое начальное R&D.
• РЕАЛЬНОЙ коммерческой эксплуатации еще нет (и непонятно, когда будет)

 

Что может помочь:

• Какое-то физическое открытие, снижающее затраты на обвязку и эксплуатацию процессоров
• Открытие чего-то, что на порядок увеличит время декогеренции и/или снизит число ошибок

 

На мой взгляд (исключительно личное мнение), в текущей научной парадигме знаний мы не добьемся значительных успехов в развитии квантовых технологий, тут нужен качественный прорыв в какой-либо области фундаментальной или прикладной науки, который даст толчок новым идеям и методам.

Ну а пока — нарабатываем опыт в квантовом программировании, собираем и создаем квантовые алгоритмы, тестируем идеи и прочее и прочее. Ждем прорыва.

Заключение

(к оглавлению)

В этой статье мы с вами прошлись по основным вехам развития квантовых вычислений и квантовых компьютеров, разобрали принцип их работы, рассмотрели основные проблемы, стоящие перед инженерами при разработке и эксплуатации квантовых процессоров, а также посмотрели что на самом деле представляют из себя многокубитные компьютеры D-Wave и недавнее заявление Google о достижении квантового превосходства.

За кадром остались вопросы программирования квантовых компьютеров (языки, подходы, методы и т.д.) и вопросы, связанные с конкретной физической реализацией процессоров, как происходит управление кубитами, связывание, считывание и т.д. Возможно, это будет тема следующей статьи или статей.

Спасибо за внимание, надеюсь эта статья будет кому-нибудь полезной.

(С) Kruegger

Благодарности

(к оглавлению)

@Oxoron за вычитку и замечания по исходному тексту, а также за статью “Характеристики квантовых компьютеров”

@a5b за информационно-насыщенные комментарии к “Характеристики квантовых компьютеров”, да и не только к ней, которые во многом помогли мне разобраться с этим пазлом.

Всем авторам статей и публикаций, материалы которых были использованы при написании этой статьи.

Список ресурсов

(к оглавлению)

Статьи о текущем положении дел от [The National Academies Press]

http://cs.brown.edu/courses/csci1800/sources/2018_NAE_QuantumComputing_ProgressAndProspects.pdf https://www.nap.edu/catalog/25196/quantum-computing-progress-and-prospects

Статьи с Хабра (в случайном порядке)

https://habr.com/ru/post/458450/ https://habr.com/ru/post/401315/ https://habr.com/ru/post/458134/ https://habr.com/ru/post/246483/ https://habr.com/ru/post/95428/ https://habr.com/ru/post/387761/ https://habr.com/ru/post/468911/ https://habr.com/ru/post/435560/ https://habr.com/ru/post/316810/ https://habr.com/ru/company/microsoft/blog/351624/ https://habr.com/ru/company/microsoft/blog/351628/ https://habr.com/ru/company/ua-hosting/blog/377533/ https://habr.com/ru/company/acronis/blog/455559/ https://habr.com/ru/company/yandex/blog/332106/ https://habr.com/ru/company/mailru/blog/350208/ https://habr.com/ru/company/mailru/blog/476444/ https://habr.com/ru/company/misis/blog/470445/ https://habr.com/ru/company/it-grad/blog/452424/ https://habr.com/ru/company/piter/blog/450480/

Источник: habr.com

Комментарии: