Популяционный алгоритм, основанный на поведении косяка рыб

В рамках данного сообщества неоднократно обсуждались генетические алгоритмы и их применение на практике. В этой статье я хотел бы поделиться относительно новым методом оптимизации функций, основанным на поведении косяка рыб в условиях поиска пищи.

Введение

С середины прошлого века велись исследования по симуляции биологических механизмов природы, в частности, связанные с процессом эволюции. Лишь только к 80-м годам начались практические испытания этих методов в связи с возникшей необходимостью в эффективных способах оптимизации n-арных функций, имеющих высокую вычислительную сложность, многоэкстремальность и т.д. Говоря о терминологии, стоит упомянуть, что данные алгоритмы относятся к классу стохастических поисковых. Во многих источниках также можно встретить такие определения, как поведенческий, интеллектуальный, метаэвристический или популяционный. Будем и мы последний термин использовать для классификации нашего алгоритма. Вообще говоря, данный алгоритм можно определить более точно, используя следующую схему.

Популяционные алгоритмы разделяются на следующие категории:

• Эволюционные алгоритмы, включая те самые генетические.
• Алгоритмы, вдохновленные живой природой (например, алгоритм оптимизации роем светлячков, кукушкин поиск и т.п.).
• Алгоритмы, вдохновленные неживой природой (например, алгоритм гравитационного поиска).
• Алгоритмы, основанные на поведении человеческого общества (например, алгоритм эволюции разума).
• Прочие алгоритмы.

Разобравшись с терминологией, перейдем непосредственно к изучению популяционного алгоритма оптимизации, основанного на поведении косяка рыб.

Разбор алгоритма

Данный алгоритм предложили в 2008 году Фило (B. Filho) и Нето (L. Neto).
Как и во всех популяционных алгоритмах, в качестве входных параметров задаются: функция приспособленности (функция, для которой необходимо найти экстремумы), область исследования этой функции и параметры работы алгоритма (о них чуть позже). В текущем алгоритме FSS (Fish School Search) область поиска представляет собой аквариум, в котором плавают агенты (рыбы). Как известно, в условиях поиска пищи рыбы плавают косяком, поэтому в нашем случае конечной целью является смещение всех агентов в область экстремума функции. В общем случае схема работы алгоритма следующая:

1. Инициализация популяции (равномерное распределение рыб в аквариуме)
2. Миграция агентов к источнику пищи (аналогия: чем больший шаг агенты совершили в направлении области экстремума функции, тем больше еды они получили)
3. Завершение поиска

Нужно больше подробностей

Стадия «Миграция агентов» выполняется поитерационно, и в каждой из итераций выполняются операторы двух групп:

1. Операторы плавания, обеспечивающие миграцию агентов в пределах аквариума.
2. Операторы кормления, фиксирующие успех исследования тех или иных областей аквариума.

Настало время поговорить о параметрах, которые имеет аквариум, и его обитатели.
Итак, введем следующие переменные, характерные для всего аквариума в целом:
populationSize - размер популяции (количество рыб в косяке).
iterationCount - количество итераций в стадии «Миграция агентов»
lowerBoundPoint, higherBoundPoint - верхняя и нижняя границы поиска
individStepStart, individStepFinal - задает начальный и конечный радиус поиска пищи вокруг агентов
weightScale - максимальный вес агента.
Это как раз те самые параметры, которые вводит пользователь. С помощью них регулируется соотношение точность/время работы алгоритма.
Сами агенты характеризуются только двумя величинами:
swimStatePos - позиция агента в разных стадиях плавания
weight - текущий вес агента

Безусловно, при программной реализации алгоритма таким количеством переменных явно не обойтись, но пока не будем усложнять себе жизнь.

Осознавая то, что программистам важнее код, чем пустая болтовня, будем углубляться в алгоритм, используя следующий псевдокод:



Замечание: все нижеследующие пояснения работы алгоритма рассчитаны на то, что решается задача условной максимизации функции, однако это не должно вызывать сомнений по поводу неработоспособности данного метода при поиске минимальных значений функции.

1. Итак, как уже было сказано, первым делом проводится инициализация всей популяции: случайный выбор позиции агента в пределах аквариума (swimStatePos[0]) и установка веса, равного половине от максимального (weight=weightScale/2) для всех рыб.
2. Далее начинается основной цикл алгоритма, который характеризует стадию «Миграция агентов к источнику пищи». В качестве критерия остановки в нашем случае используется величина «Количество итераций» (iterationCount).
3. Затем наступает индивидуальная стадия плавания агентов. Она характеризуется тем, что все рыбы в некоторой области вокруг себя (individStep) пытаются найти лучшее значение функции.
   Если им это удается, то этот шаг фиксируется. В противном случае
   
   считаем, что этого перемещения не было.
4. Теперь необходимо закрепить успех в индивидуальной стадии плавания. Для этого используется характеристика «Вес». Она равняется изменению функции приспособленности для данного агента до и после индивидуальной стадии, нормированного максимальным изменением функции среди популяции:
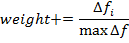
   . Вообще говоря, это является отличительной особенностью данного алгоритма, так как нам не надо запоминать лучших агентов на предыдущих итерациях.
5. После этого рыбы совершают следующую стадию плавания - инстинктивно-коллективную. Для всего косяка рыб высчитывается величина «Общий шаг миграции»: .
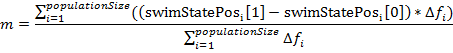   Смысл ее следующий: на каждого агента влияет вся популяция в целом, при этом влияние отдельного агента пропорционально его успехам в индивидуальной стадии плавания. Затем вся популяция смещается на подсчитанную величину m:
   
   
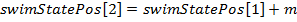
6. Перед следующей операцией плавания необходимо выполнить промежуточные действия, а именно: подсчитать центр тяжести всего косяка:
   .
7. Мы, а точнее, рыбы, перешли к последней стадии плавания: коллективно-волевой. Здесь необходимо узнать, как изменился вес популяции по сравнению с предыдущей итерацией. Если он увеличился, значит популяция приблизилась к области максимума функции, поэтому необходимо сузить круг его поиска, тем самым проявляются интенсификационные свойства. И наоборот: если вес косяка уменьшился, значит агенты ищут максимум не в том месте, поэтому необходимо изменить направление траектории и проявить диверсификационные свойства.
   
   Величина collStep в следующей формуле отвечает за шаг волевого смещения. Рекомендуется использовать значение, в 2 раза большее индивидуального шага поиска. Оператор dist высчитывает расстояние между двумя точками в евклидовом пространстве.
   
   (Величины, отвечающие за положение агентов, являются структурными типами n-мерной точки, для которых определены следующие операции: сложение/вычитание двух точек, сложение/вычитание точки и числа, умножение/деление точки и числа, а также операции сравнения точек. Чтобы избежать этой геометрической бессмыслицы, принято считать данные величины за векторные типы данных, доопределив некоторые операции)
8. Последним оператором в итерации является линейное уменьшение шага индивидуального поиска для следующей итерации. На самом деле, это является уже модификацией стандартного алгоритма FSS для повышения эффективности поиска, которая выполняется по такой формуле:
   

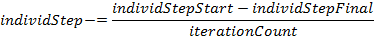
Реализация и тестирование

Реализация

Данный алгоритм лег в основу моей курсовой работы («Программа оптимизации, инспирированная поведением косяка рыб»), которая была представлена на защите 26 апреля. Возможно, кто-то заинтересуется, почему так рано сдавали курсовые. Не мудрствуя лукаво, скажу лишь, что это все часть плана по отчислению студентов с 1-го курса факультета БИ (отделение ПИ) НИУ ВШЭ, которые оказались в лапах учебной части, грозящей весь год 30%-ным отчислением (на обратной стороне монеты гордо красуется агитационный лозунг: «Мы примем всех, и если надо будет, оплатим места за свой счет»). В рамках регламента курсовых работ, реализация велась на языке C# 4.0, в качестве графической составляющей была выбрана библиотека OpenTK (представляет обертку OpenGL для .NET), заданные пользователем функции парсились с помощью библиотеки, реализованной на хабре ранее. К сожалению, исходники выложить не могу (код далеко не совершенен, сам много раз это осознавал), а вот саму программу предоставлю на всеобщее усмотрение (ссылки в конце статьи). А пока просто скриншотик главного окна:

Тестирование

Для популяционных алгоритмов тестирование представляет собой увлекательную вещь, потому что результат его работы в значительной степени зависит от входных параметров. В рамках этой статьи рассмотрим следующие 2 графика.

1. 
   
   • Область поиска: от (-100;-100) до (100; 100)
   • Количество итераций: 100
   • Размер популяции: 50
   • Начальный индивидуальный шаг: 10
   • Конечный индивидуальный шаг: 0.1
   • Максимальный вес рыбы: 50
   
   Итак, к концу работы алгоритма максимальное значение функции равнялось 9,999978..., а среднее значение 9,999148- График изменения среднего значения выглядит следующим образом:
   
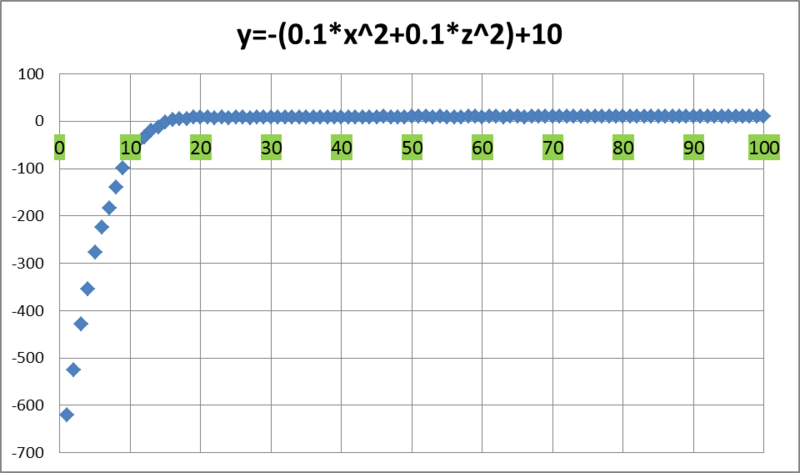
   То есть уже на 15-й итерации косяк рыб находился в положительной полуплоскости по оси OY. А начиная с 48-й итерации среднее значение функции не опускалось ниже 9-ти. А вот и полная картина происходящего (вид с верхушки айсберга):
   
   
   
2. 
   
   • Область поиска: от (-100;-100) до (100; 100)
   • Количество итераций: 100
   • Размер популяции: 50
   • Начальный индивидуальный шаг: 10
   • Конечный индивидуальный шаг: 0.1
   • Максимальный вес рыбы: 50
   
   
   К концу работы алгоритма максимальное значение функции равнялось 19,999996..., а среднее 19,9994- Динамика среднего значения такова:
   
   
   Уже с 42 итерации среднее значение функции держалось на отметке не ниже 19-ти. Анимация того, как алгоритм справляется с многоэкстремальными функциями (для Habrastorage файл слишком велик, так что возможны проблемы с отображением картинки):
   
   

Источники

• Скачать программу можно тут (в комплект входят: программа для исследования функций от двух переменных с отчетами по функциям из данной статьи, консольная версия программы со встроенными функциями от N переменных, описание языка задания фитнесс-функций (по ГОСТу, между прочим))
• Пожалуй, единственная русскоязычная статья, в которой описан данный алгоритм: Карпенко А. П. «Популяционные алгоритмы глобальной поисковой оптимизации. Обзор новых и малоизвестных алгоритмов». Скачать.
• Веб-сайт, целиком посвященный Fish School Search
• И еще одна полезная статья на английском
• Исходники консольной версии программы (можно форкать)

.S.

Спасибо за прочтение статьи! С радостью отвечу на ваши вопросы в комментариях.

UPD: Добавил исходные коды.

Источник: habrahabr.ru

Комментарии: