DeepMath-103K: датасет для обучения с подкреплением моделей рассуждения от Tencent

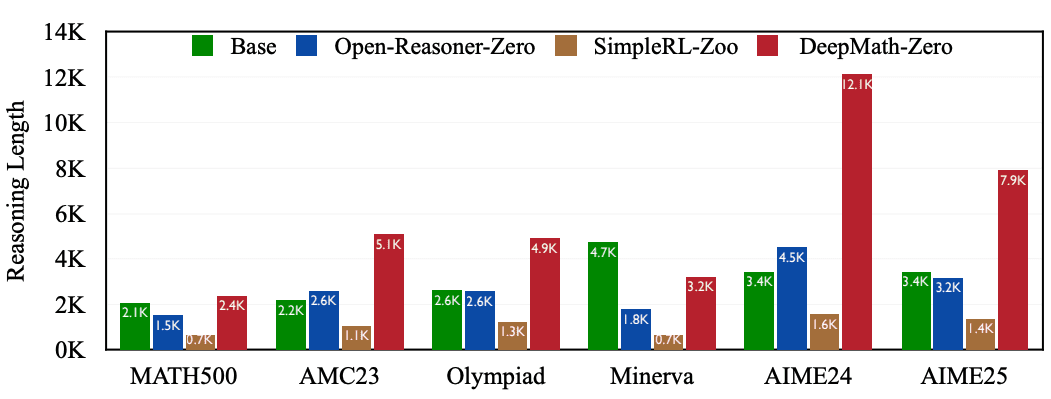
Исследователи из Tencent и Шанхайского университета Цзяо Тонг опубликовали DeepMath-103K — крупный математический датасет, созданный для разработки продвинутых моделей рассуждения с помощью обучения с подкреплением. Создание набора данных стоило исследователям 138 000 долларов США на API-кредиты GPT-4o и 127 000 часов работы GPU H20.

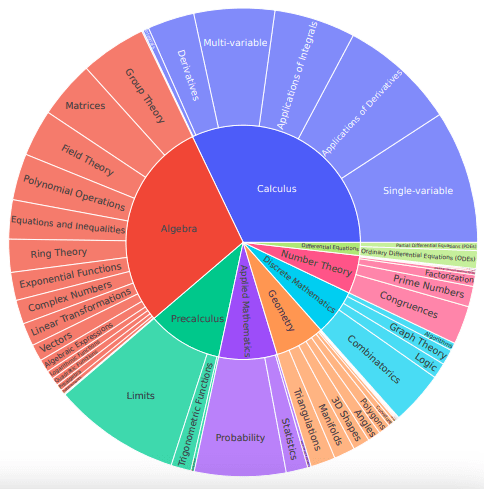
DeepMath-103K устраняет ограничения существующих наборов данных. Он содержит 103 тысячи математических задач, из которых 95 тысяч — специально отобранные сложные примеры (уровни 5-10) и 8 тысяч дополнительных задач (уровни 3-5), что дает фокус на задачах высокой сложности. Каждая задача включает проверяемый окончательный ответ, что позволяет применять основанные на правилах функции вознаграждения, необходимые для фреймворков RL.

Каждая задача в наборе сопровождается тремя решениями, сгенерированными моделью Deepseek R1, что позволяет поддерживать разные методы обучения: supervised fine-tuning, reward modeling и model distillation. Набор данных был очищен от пересечений с популярными тестовыми наборами, такими как MATH, AIME, AMC, Minerva Math и OlympiadBench, что позволяет объективно оценивать результаты обучения моделей.

Процесс создания набора данных

Набор данных DeepMath-103K был создан с помощью четырехэтапного процесса. На начальном этапе исследователи провели анализ источников, изучая распределение сложности в открытых датасетах и выбирая те, которые имеют высокую концентрацию сложных задач, в основном MMIQC и WebInstructSub. Затем был проведен этап очистки данных, во время которого с помощью алгоритмов поиска сходства по эмбеддингам и оценки языковыми моделями выявлялись исключались задачи, схожие с тестовыми вопросами из известных наборов.

Третий этап включал фильтрацию по сложности, где задачи классифицировались с использованием руководящих принципов Art of Problem Solving (AoPS). Оставили только те, которые имели уровень сложности 5 или выше. На заключительном этапе исследователи верифицировали, что каждая задача имеет проверяемый окончательный ответ и несколько путей решения. Это важно для методов обучения с подкреплением на основе правил.

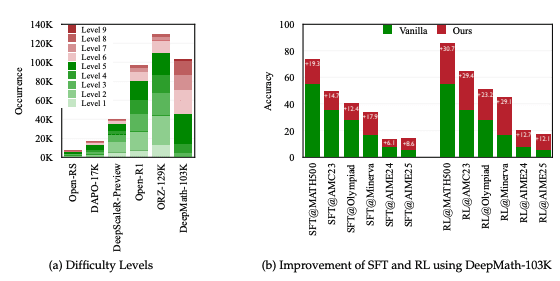
Результаты обучения моделей на датасете DeepMath-103K

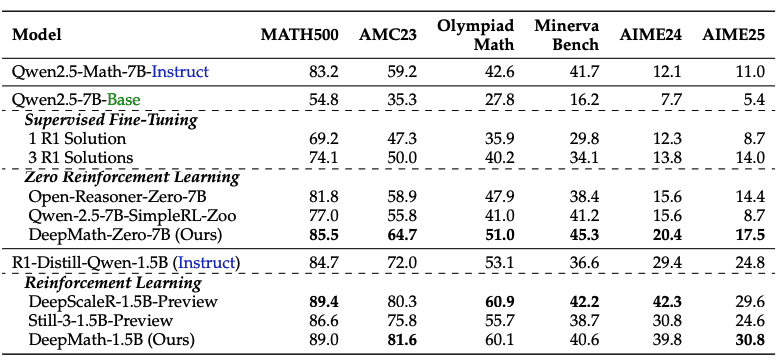
Модели, обученные с использованием DeepMath-103K, показали значительное улучшение результатов на математических тестах. На MATH500 модель, обученная на DeepMath-103K с RL-Zero, улучшила точность с 54,8% до 85,5% — прирост в 30,7 процентных пункта. На тесте AIME24 улучшение составило с 7,7% до 20,4%: производительности выросла в 2,6 раза.

Эффективность набора данных подтверждается результатами на других тестах: AMC23 показал улучшение точности с 35,3% до 64,7%, точность ответов в задачах из олимпиад по математике улучшились с 27,8% до 51,0%. При применении к моделям, уже прошедшим supervised fine-tuning для математических рассуждений, DeepMath-103K повысил точность на AIME25 с 24,8% до 30,8%.

DeepMath-103K поддерживает несколько парадигм обучения. В сценариях supervised fine-tuning множественные пути решения позволяют моделям изучать разные методы решения задач. В model distillation различные сценарии решения способствуют передаче знаний от более крупных моделей к меньшим, повышая эффективность при сохранении точности.