Сортировка слиянием на CUDA

МЕНЮ

Главная страница
Поиск
Регистрация на сайте
Помощь проекту
Архив новостей

ТЕМЫ

Новости ИИРазработка ИИВнедрение ИИРабота разума и сознаниеМодель мозгаРобототехника, БПЛАТрансгуманизмОбработка текстаТеория эволюцииДополненная реальностьЖелезоКиберугрозыНаучный мирИТ индустрияРазработка ПОТеория информацииМатематикаЦифровая экономика

Авторизация

RSS

RSS новости

Основываясь на своем предыдущем посте об алгоритмах сортировки, я реализовал те же алгоритмы с использованием CUDA для исследования улучшений производительности посредством параллельных вычислений. Цель состоит в том, чтобы увидеть, как мы можем использовать мощь параллельных вычислений для ускорения наших алгоритмов сортировки. Несколько дней назад я пошел на мероприятие по набору сотрудников NVIDIA, это было отличное мероприятие, и оно мотивировало меня попробовать переписать алгоритмы сортировки с использованием CUDA.

В качестве тестового алгоритма я выберу сортировку слиянием, поскольку она удачно разделяет задачу на меньшие подзадачи с двумя равными половинами, что хорошо подходит для параллельных вычислений.

Базовая рекурсивная сортировка слиянием сверху вниз

Ниже представлена базовая логика сортировки слиянием сверху вниз, где я рекурсивно делю массив на две половины, пока не достигну базового случая одного элемента, а затем снова объединяю отсортированные половины.

Чтобы объединить два отсортированных массива, мы сравниваем их начальные элементы, выбираем меньший из них для выходного массива и перемещаем указатели вперед.

MERGE_SORT(arr, left, right)     IF left < right THEN         mid <- left + (right - left) / 2          // Recursively sort first half         MERGE_SORT(arr, left, mid)          // Recursively sort second half         MERGE_SORT(arr, mid + 1, right)          // Merge the sorted halves         MERGE(arr, left, mid, right)     ENDIF END MERGE_SORT

Теперь давайте рассмотрим реализацию ЦП, ссылка на которую приведена ниже:

Код: Базовая рекурсивная сортировка слиянием на CPU

Примечания:

  • Сигнатуры функций:
    • void merge(uint8_t* arr, uint8_t* temp, long long left, long long mid, long long right):
      • uint8_tвместо этого intдля элементов массива делается для сохранения небольших значений (0-255)
      • long longдля индексов допускается очень большой массив (10^18)
      • uint8_t* tempдействует как рабочее пространство для операции слияния и обеспечивает повышение производительности
    • void mergeSort(uint8_t* arr, uint8_t* temp, long long left, long long right)следует псевдокод, который делит массив на две половины и вызывает себя на этих двух половинах. Когда он достигает базового случая одного элемента, он вызывает функцию merge, чтобы снова объединить две половины вместе.
  • Сортировка GPU и CPU:
    • Массивы генерируются с переданными аргументами с определенным начальным числом (например, 1)
    • Все реализации выполняют примерно одинаковый объем работы.
    • Результат сортировки слиянием необходимо вызвать обратно в исходный массив из графического процессора в центральный процессор, что является накладными расходами, и сравнить с отсортированным массивом с использованием std::sortцентрального процессора.
    • Лучшим сравнением может быть сортировка случайных массивов на самом GPU и сравнение результатов.
    • То, как и где мы сортируем, имеет большое значение в зависимости от более широкого контекста использования.
  • Wall Clock timeдля построения графиков используется время выполнения всей программы, а не только время, затраченное на сортировку массива
  • Correctness checkingвыполняется путем сортировки исходного массива с помощью std::sortи сравнения результатов
  • Временная сложность в среднем случае: O(n log n)
  • Сложность пространства: O(n)

Базовая рекурсивная сортировка слиянием сверху вниз в CUDA

Теперь давайте посмотрим, как мы можем реализовать это в CUDA. Это следует той же схеме, что и реализация на CPU. Это моя первая наивная реализация на CUDA. Ядро запускается для каждой операции слияния, а рекурсия выполняется на CPU.

Код: Базовая рекурсивная сортировка слиянием с использованием CUDA

Примечания:

  • #include <cuda_runtime.h>обеспечивает доступ к API среды выполнения CUDA и таким функциям, как cudaMalloc(), cudaMemcpy(), cudaFree(), kernel<<<numBlocks, threadsPerBlock>>>(args),cudaGetErrorString()cudaGetLastError()
  • __global__ void mergeSort(uint8_t* arr, uint8_t* temp, long long left, long long right)это функция ядра, которая запускается для каждой операции слияния, которая на данный момент делает то же самое, что и реализация CPU
  • В пределахvoid mergeSort(....)
    • merge<<<1, 1>>>(...)запускает ядро для каждой операции слияния, но сейчас просто запускает один поток для выполнения всего слияния, что неэффективно. <<<1,1>>>указывает количество блоков потоков и количество потоков на блок потоков. <<<numBlocks, blockSize>>>— это синтаксис для запуска ядра в CUDA. Общее количество потоков, которые у вас есть, равно , numBlocks * blockSizeи они могут быть организованы в одномерной, двухмерной или трехмерной сетке.
    • cudaDeviceSynchronize()заставляет его ждать завершения этого слияния, прежде чем переходить к следующему этапу, чтобы избежать проблем с корректностью.
    • cudaMalloc(....)используется для выделения памяти на графическом процессоре cudaMemcpy(..., cudaMemcpyHostToDevice)и cudaMemcpy(...., cudaMemcpyDeviceToHost)может использоваться для копирования данных между центральным процессором и графическим процессором.
    • cudaFree(cu_arr)используется для освобождения памяти на графическом процессоре.

Сравнение реализации базовой рекурсивной сортировки слиянием на CPU и GPU

Эта реализация не очень эффективна, как вы можете видеть на рисунке 1, ядро запускается для каждой операции слияния, а рекурсия выполняется на CPU. CUDA не обрабатывает рекурсию эффективно, поэтому нам нужно свести рекурсию в цикл.

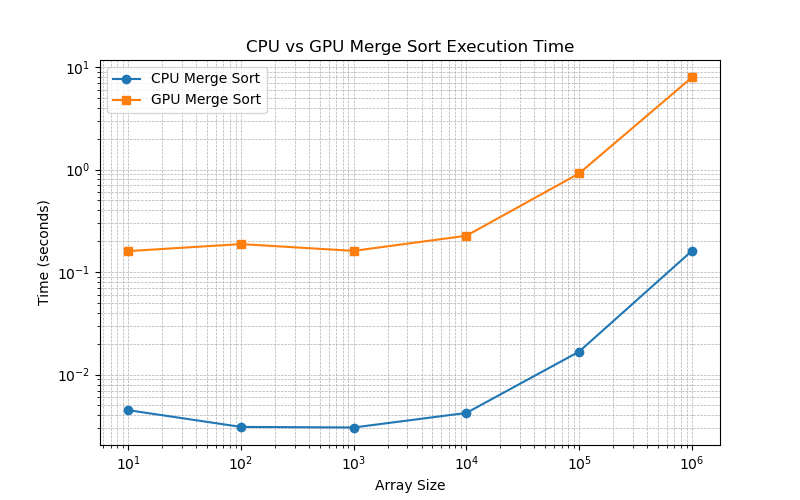
У меня возникли важные вопросы:

  • Почему CUDA плохо справляется с рекурсией?
    • Наша функция слияния запускается как один поток на GPU, а рекурсия выполняется на CPU. Глубокая рекурсия проблематична, так как может привести к переполнению стека, учитывая небольшой размер потоков на GPU. Для каждой операции слияния существуют нетривиальные накладные расходы на запуск ядра. Рекурсия не допускает большого параллелизма. Синхронизация также является проблемой.
  • Как мы можем улучшить ситуацию?
    • Перепишите рекурсию в итеративный цикл и выполните сортировку слиянием снизу вверх.

В отличие от реализаций на базе ЦП, где рекурсия широко используется, CUDA требует итерационного подхода с тщательным управлением памятью и синхронизацией потоков для достижения оптимальной производительности, как показано в реализациях ниже.

Итеративная сортировка слиянием снизу вверх

Поскольку CUDA неэффективно обрабатывает рекурсию из-за ограничений стека, вместо этого мы реализуем итеративный подход для сортировки слиянием. Суть итеративного подхода заключается в слиянии массива снизу вверх. Мы начинаем с слияния наименьших подмассивов размером 1, затем слияния подмассивов размером 2, затем 4, 8, 16 и т. д.

MERGE_SORT(arr, temp, start, end)     FOR sub_size <- 1 TO end STEP 2 x sub_size DO         FOR left <- 0 TO end STEP 2 x sub_size DO             mid <- MIN(left + sub_size - 1, end)             right <- MIN(left + 2 x sub_size - 1, end)              MERGE(arr, temp, left, mid, right)         ENDFOR     ENDFOR END MERGE_SORT

Теперь давайте рассмотрим реализацию ЦП, ссылка на которую приведена ниже:

Код: Итеративная сортировка слиянием на CPU

Примечания:

void mergeSort(uint8_t* arr, uint8_t* temp, long long n) {     long long left, mid, right, size;     for (size = 1; size < n; size *= 2) {         for (left = 0; left < n - size; left += 2 * size) {             mid = left + size - 1;             right = std::min(left + 2 * size - 1, n - 1);             mergeKernel(arr, temp, left, mid, right);         }     } }

Мы превратили рекурсию в цикл:

  • Top for loopувеличивает размер из 1 to nв powers of 2так что у нас есть размеры 1,2,4,8. Можно было бы беспокоиться о том, что массивы, которые не очень хорошо подходят как степени 2, это тоже было для меня беспокойством, и это прекрасно обрабатывается clamping the right index to the end of the array.
  • Inner for loopпроходит по массиву с шагом 2*размер и объединяет подмассивы размером, sizeначиная с leftдо rightи midявляется серединой подмассива. Обратите внимание, right = std::min(left + 2 * size - 1, n - 1);что прикрепляет правый индекс к концу массива.
  • mergeKernelто же самое, что и mergeфункция в рекурсивном подходе, но теперь она вызывается в цикле.

Итеративная сортировка слиянием снизу вверх в CUDA

Лично для меня главный вывод из этой реализации. В вышеприведенной реализации есть два цикла, поэтому я подумал сделать второй цикл параллельно на GPU, который в основном выполняет операции слияния параллельно для всего массива.

void mergeSort(uint8_t* arr, uint8_t* temp, long long n) {     bool flipflop = true;     long long numThreads, gridSize;     long long size; // size means the merge arrays sizes     for (size = 1; size < n; size *= 2) {         numThreads = max(n / (2 * size), (long long)1);         gridSize = (numThreads + THREADS_PER_BLOCK - 1) / THREADS_PER_BLOCK;         mergeKernel<<<gridSize, THREADS_PER_BLOCK>>>(flipflop ? arr : temp, flipflop ? temp : arr, size, n);         CUDA_CHECK(cudaGetLastError());         CUDA_CHECK(cudaDeviceSynchronize());         flipflop = !flipflop;     }      if (!flipflop) CUDA_CHECK(cudaMemcpy(arr, temp, n * sizeof(uint8_t), cudaMemcpyDeviceToDevice)); }

Примечания:

  • flipflopиспользуется для отслеживания того, какой массив является окончательно отсортированным массивом, а какой — рабочим пространством.
  • numThreads— это количество потоков, которые нам необходимо запустить для операции слияния. gridSize— это количество блоков, которые нам необходимо запустить.
  • После вычисления размера объединенных массивов:
    • Учитывая размер массивов слияния, слияние происходит на двух подмассивах размера size. Поэтому мне нужно запустить n / (2 * size)потоки (что 1 помогает в случае, когда размер становится больше n/2).
    • gridSizeрассчитывается путем деления числа потоков на THREADS_PER_BLOCKи округления вверх. Размер сетки — это количество блоков, которые нам нужно запустить.
    • В mergeKernel мы указываем gridSize и THREADS_PER_BLOCK для запуска ядра. mergeKernel<<<gridSize, THREADS_PER_BLOCK>>>(flipflop ? arr : temp, flipflop ? temp : arr, size, n);Обратите внимание на тернарный оператор для переключения между массивами, в качестве которых выступают arr и temp, где ping-pong buffersв зависимости от состояния триггера мы считываем данные из одного и записываем данные в другой.
    • CUDA_CHECK(cudaGetLastError());и CUDA_CHECK(cudaDeviceSynchronize());используются для проверки ошибок и для того, чтобы убедиться, что ядро завершило выполнение перед переходом к следующему этапу.
  • if (!flipflop) CUDA_CHECK(cudaMemcpy(arr, temp, n * sizeof(uint8_t), cudaMemcpyDeviceToDevice));используется для копирования окончательно отсортированного массива обратно в исходный массив, если окончательно отсортированный массив находится во временном массиве.

Теперь давайте посмотрим на mergeKernel, который показан:

__global__ void mergeKernel(uint8_t* arr, uint8_t* temp, long long curr_size, long long n) {     long long index = blockIdx.x * blockDim.x + threadIdx.x;     long long left = 2 * curr_size * index;     if (left >= n) return;       long long mid = min(left + curr_size - 1, n - 1);     long long right = min(left + 2 * curr_size - 1, n - 1);      long long i = left, j = mid + 1, k = left;      ///.... below is the good old merge logic }

Примечания:

  • Мне потребовалась уйма времени, чтобы понять индексацию и как правильно запустить ядро для операции слияния. Я запускаю 1d grids и 1d blocks. blockIdx.xдает индекс блока, который может быть 1,2,3,4,…, а затем blockDim.xуказывает количество потоков в блоке. blockIdx.x * blockDim.xпосле того, как мы добавляем его threadIdx.x(0 к THREADS_PER_BLOCK-1), дает индекс потока глобально, где каждый индекс уникален.
  • Теперь мы можем однозначно идентифицировать наш поток глобально, мы хотим дать ему в unique subproblemзависимости от этого index. Теперь мы переключаем наше внимание на вычисление индексов left, mid, и rightдля подмассива, который мы хотим объединить. У нас есть массив размером n, каждый поток должен иметь дело с подзадачами размером 2 * curr_sizeот leftдо right.
  • Most Important question: сколько у меня индексов? index= blockIdx.x * blockDim.x + threadIdx.xи если blockIdx.x равен 0 и threadIdx.x равен 0, то минимальный индекс равен 0. Мы знаем, что max blockIdx.x равен gridSize-1. Поэтому максимальный индекс создается (gridSize-1) * blockDim.x + blockDim.x - 1как gridSize * blockDim.x -1max. Если мы заменим gridSize на numThreads + THREADS_PER_BLOCK -1 / THREADS_PER_BLOCKи blockDim.x на THREADS_PER_BLOCK, то получим numThreads + THREADS_PER_BLOCK - 2. Таким образом, максимальный индекс приблизительно n / 2 x curr_sizeсоответствует нашим подзадачам с некоторыми дополнительными потоками.
  • Учитывая, что у нас есть индексы от 0 до n/2 * curr_size, мы можем вычислить left indexas 2 * curr_size * index, который примерно покрывает весь массив. Если у нас есть, left >= nмы возвращаемся, поскольку мы покрыли весь массив. Был интересный пограничный случай, когда этот left ранее был intведущим к переполнению, и мне пришлось изменить его на long long, я обнаружил эту ошибку с помощью compute-sanitizerи с помощью отладочных символов с помощью -g -Gпри компиляции с nvcc.
  • После того, как мы находим left, mid, right, применяется та же старая логика слияния.
  • Я пробовал разные значения, THREADS_PER_BLOCKно результаты были почти такими же.

Результаты

Мы определили задачу генерации случайных массивов на CPU, выполнения сортировки на CPU/GPU, а затем сравнения со стандартным методом сортировки std::sortна CPU.

  • Итеративная сортировка слиянием снизу вверх в CUDA значительно повышает эффективность за счет распараллеливания операций слияния
  • Неудивительно, что CPU approachesдля меньших массивов общий показатель времени выполнения программы улучшается.
  • thrust::sortоказывается лучше, чем мои реализации для больших массивов, где GPU iterative methodрекурсивный reasonably competitiveподход сильно отстает.
  • CPUподходы, такие как рекурсивный и итеративный, весьма конкурентоспособны сstd::sort
  • 10^7 — это переломный момент, когда сортировка на GPU thrust::sortпревосходит стандартную сортировку на CPU, а моя реализация GPU iterativeтакже очень близка к этому.
  • Накладные расходы на отправку данных на графический процессор и получение данных обратно с графического процессора, вероятно, являются причиной разницы во времени между подходами CPU и GPU для размеров от 10^1 до 10^4.

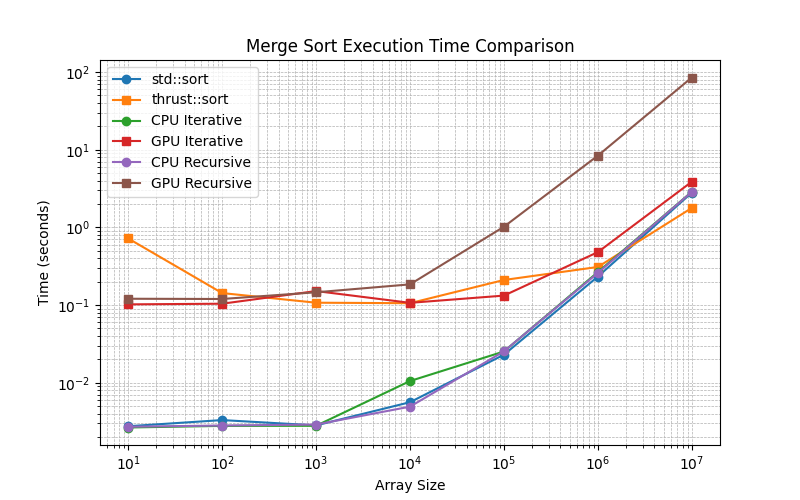
Заключение и будущая работа

Я узнал много нового о сортировке слиянием, которая долгое время меня не касалась. Этот простой алгоритм также дал прекрасную возможность изучить основы CUDA на среднем уровне сложности. Есть несколько вещей, которые я мог бы сделать лучше и хотел бы изучить в будущем:

  • Определите задачи лучше или больше задач, где цели могли бы быть:
    • Все должно начинаться с CPU и заканчиваться на GPU только для дальнейших вычислений или наоборот.
    • Все должно начинаться и заканчиваться только на отдельных устройствах.
    • Все должно начинаться на GPU и переходить на CPU для дальнейших вычислений.
  • Попытка реализации Parallel Merge Sort, как предложено Prof Rezaulв SBUссылках [1]
  • Сравните, насколько большие массивы поступают с устройства, 10^7 to 10^18и stress testingсколько сортировок мы можем выполнить на каждом из них.
  • Оптимизируйте производительность на GPU еще больше shared memory, используя thrust:sortat specific levelв сочетании с моей реализацией, как мы делаем длинное умножение в алгоритме Карацубы для размера n < 20, как меня CSE 201научил Prof Sesh.
  • Используйте потоки в реализациях ЦП, чтобы увидеть, может ли это быть полезным для повышения производительности.
  • Сравните эффекты использования различных размеров THREAD_PER_BLOCKи, возможно, вместо того, чтобы каждый поток решал одну подзадачу, each threads solve more than 1 subproblemsучитывая, что мы ждем завершения всех потоков.

Источник: ashwanirathee.com

Комментарии: