Сложность алгоритмов. Разбор Big O

Сложность алгоритмов - это ключевой аспект при проектировании и создании веб-приложений, особенно при работе с большим объемом данных или выполнении вычислительно сложных операций. Понимание, как оценивать сложность алгоритмов, помогает принимать обоснованные решения в выборе алгоритмов и структур данных, а также оптимизировать производительность своих приложений.

Сейчас мы рассмотрим, почему знание сложности алгоритмов является важным навыком для разработчика, какие методы используются для оценки сложности, и какие практические применения можно найти для этого знания при создании веб-приложений. На тему сложности алгоритмов часто задаются вопросы на техническом собеседовании.

Пример

Давайте представим, что у вас есть интернет-магазин, на котором пользователи могут искать продукты по разным параметрам, таким как цена, бренд, категория и другие фильтры.

Ваша задача - обеспечить быстрый и удобный поиск для пользователей.

Если вы не учтете сложность алгоритмов, то при реализации поиска вы можете выбрать неоптимальный алгоритм, который будет медленно обрабатывать запросы пользователей при большом количестве товаров. Например, вы можете реализовать поиск, который каждый раз просматривает все товары и сравнивает их с запросом пользователя.

Однако, если вы знаете сложность алгоритмов, то сможете выбрать более эффективный алгоритм для поиска, такой как бинарный поиск или хэш-таблицы. Эти алгоритмы имеют лучшую производительность и работают намного быстрее, даже если у вас есть большой каталог товаров.

Таким образом, знание сложности алгоритмов позволяет вам оптимизировать функциональность вашего интернет-магазина и обеспечить пользователям быстрый и удобный поиск, что может существенно повысить уровень удовлетворенности клиентов и увеличить конверсию.

Big O

Чтобы сравнивать алгоритмы по сложности сначала мы должны узнать что такое Big O.

Big O - это термин из области анализа сложности алгоритмов и структур данных в информатике. Он используется для оценки верхней границы (наихудшего случая), временной сложности алгоритма.

Простыми словами Big O показывает как будет меняться производительность алгоритма с зависимости от роста входящих данных.

Если мы будем увеличивать количество входящих данных, то у нас может расти количество операций и время за которое выполнится алгоритм. Так же может расти количество памяти используемой данным алгоритмом для обработки входного объема данных. Big O будет показывать скорость роста времени исполнения алгоритма.

Big O называется так из-за того, что в математике "O" используется для обозначения "order of" (порядка) и позволяет сравнивать функции роста. Он представляет собой математическую нотацию, которая описывает, как алгоритм будет выполняться в наихудшем случае, исходя из размера входных данных.

Примеры нотаций Big O

• O(1): Константная сложность. Время выполнения алгоритма не зависит от размера входных данных. Например, доступ к элементу массива по индексу.

• O(log n): Логарифмическая сложность. Время выполнения алгоритма растет медленно с увеличением размера входных данных. Например, бинарный поиск в отсортированном массиве.

• O(n): Линейная сложность. Время выполнения алгоритма пропорционально размеру входных данных. Например, просмотр всех элементов в массиве.

• O(n log n): Линейно-логарифмическая сложность. Время выполнения алгоритма растет быстрее, чем линейно, но медленнее, чем квадратично. Например, сортировка слиянием (merge sort).

• O(n^2): Квадратичная сложность. Время выполнения алгоритма зависит от квадрата размера входных данных. Например, сортировка пузырьком (bubble sort).

• O(n^3): Кубическая сложность. Время выполнения алгоритма зависит от размера входных данных в кубе. Например, алгоритмы, которые имеют три вложенных цикла, такие как некоторые методы многомерной обработки данных.

• O(n!): Факториальная сложность. Это самая высокая степень роста времени выполнения алгоритма. Время выполнения алгоритма растет факториально от размера входных данных. Этот тип сложности встречается, например, при переборе всех возможных комбинаций элементов, что делает его чрезвычайно неэффективным для больших значений n.

С каждым из этим пунктом мы познакомимся на примерах.

Другие обозначения сложности алгоритмов.

Кроме обозначения "Big O", существуют другие обозначения для оценки сложности алгоритмов.

Вот несколько наиболее распространенных обозначений:

1. Big Theta (?): Big Theta также оценивает верхнюю и нижнюю границы временной сложности алгоритма, но описывает точную сложность, а не только наихудший случай, как Big O. ?(f(n)) обозначает, что время выполнения алгоритма ограничено функцией f(n) как сверху, так и снизу.

2. Big Omega (?): Big Omega оценивает нижнюю границу временной сложности алгоритма. ?(f(n)) говорит о том, что алгоритм выполнится не быстрее, чем функция f(n).

3. Little O (o): Little O представляет собой верхнюю границу, которая строже, чем Big O. Если f(n) является o(g(n)), это означает, что время выполнения алгоритма ограничивается функцией g(n), но алгоритм работает быстрее, чем g(n).

4. Little Omega (?): Little Omega представляет собой нижнюю границу, которая строже, чем Big Omega. Если f(n) является ?(g(n)), это означает, что алгоритм работает медленнее, чем g(n), но не медленнее, чем f(n).

Эти обозначения помогают более точно определить сложность алгоритма и учитывать как наихудший, так и лучший случай его работы. Когда разработчики анализируют алгоритмы, они могут использовать Big O, Big Theta, Big Omega, Little O и Little Omega в зависимости от конкретного контекста и требований задачи.

Мы уделим внимание именно Big O, так как это обозначение используется чаще всего.

Константная сложность O(1)

O(1) называют константной сложностью.

Оценка временной сложности O(1) означает, что алгоритм имеет постоянную сложность.

Под n мы будем иметь ввиду размер входящих данных.

В JavaScript чаще всего мы храним набор данных в массивах.

Размер массива, то есть его значение свойства length и будет значение n.

При константной сложности вне зависимости от размера входных данных (n), время выполнения алгоритма остается постоянным и не зависит от объема данных.

Это самый быстрый и эффективный вид временной сложности.

Примеры алгоритмов с оценкой временной сложности O(1):

• Доступ к элементу в массиве по индексу. Например, если у вас есть массив с данными, вы можете мгновенно получить доступ к элементу массива, указав его индекс, независимо от размера массива.

• Вставка или удаление элемента в конец списка (очереди) фиксированной длины. В этом случае операция выполняется быстро и не зависит от количества элементов в списке.

Оценка временной сложности O(1) является идеальной с точки зрения производительности. Однако в реальных задачах она не всегда достижима, и в большинстве случаев оценка временной сложности будет выше.

Давайте рассмотрим эту сложность на примере:

function getLastElement(arr) { 	return arr[arr.length - 1 ] }

Функция getLastElement имеет временную сложность O(1) потому, что она выполняет одну операцию - получение последнего элемента массива arr.

Независимо от размера массива, функция всегда выполняет одно действие, поэтому ее сложность остается постоянной и равной O(1). Это означает, что время выполнения функции не зависит от количества элементов в массиве и всегда будет быстрым и постоянным.

Линейная сложность O(n)

O(n) называют линейной сложностью.

Линейный рост - это понятие, которое описывает зависимость между двумя величинами, при которой одна величина увеличивается пропорционально увеличению другой.

Оценка временной сложности O(n) означает, что время выполнения алгоритма растет линейно с увеличением размера входных данных.

function findMax(arr) {     let max = arr[0];     for (let i = 1; i < arr.length; i++) {         if (arr[i] > max) {             max = arr[i];         }     }     return max; } 

В этом примере findMax ищет максимальное значение в массиве arr.

Алгоритм начинает с предположения, что первый элемент массива (arr[0]) является максимальным, а затем линейно (то есть по одному элементу) перебирает остальные элементы, сравнивая каждый с текущим максимальным. Сложность этого алгоритма O(n), так как время выполнения растет линейно с увеличением количества элементов в массиве arr.

При линейном росте при увеличении размера входных данных вдвое, то время выполнения алгоритма также увеличится примерно вдвое. Если увеличите размер данных в 10 раз, то время выполнения увеличится приблизительно в 10 раз, и так далее.

Линейный рост характерен для алгоритмов, которые выполняют постоянное количество операций для каждого элемента входных данных.

Логарифмическая сложность O(log n)

O(log n) называют логарифмической сложностью.

Оценка временной сложности O(log n) означает, что время выполнения алгоритма увеличивается логарифмически с увеличением размера входных данных (n). Другими словами, алгоритм становится медленнее, но не линейно, а медленнее в соответствии с логарифмической функцией.

Пример алгоритма с оценкой временной сложности O(log n) - бинарный поиск. В этом алгоритме на каждом шаге половина данных отсекается, и поиск продолжается в оставшейся половине. Это означает, что при увеличении размера входных данных вдвое, бинарный поиск требует всего одного дополнительного шага.

Таким образом, алгоритмы с оценкой временной сложности O(log n) эффективны и быстры при работе с большими объемами данных, так как их производительность ухудшается медленно с увеличением размера данных.

Пример функции бинарного поиска на JavaScript, которая имеет сложность O(log n):

function binarySearch(arr, target) {     let left = 0;     let right = arr.length - 1; while (left <= right) {     let mid = Math.floor((left + right) / 2);      if (arr[mid] === target) {         return mid; // элемент найден     } else if (arr[mid] < target) {         left = mid + 1; // искать в правой половине     } else {         right = mid - 1; // искать в левой половине     } }  return -1; // элемент не найден  } 

Бинарный поиск ищет значение в отсортированном массиве, разделяя его пополам на каждой итерации. Поиск начинается с середины массива. Если значение, которое мы ищем, больше среднего элемента, поиск продолжается в правой половине массива. Если оно меньше, то в левой. Таким образом, на каждой итерации мы уменьшаем область поиска примерно в два раза, что обеспечивает логарифмическую сложность O(log n).

Квадратичная сложностьO(n^2)

O(n^2) означает квадратичную сложность алгоритма, где время выполнения растет пропорционально квадрату размера входных данных. Это часто возникает в алгоритмах с вложенными циклами, когда каждый элемент первого списка обрабатывается с каждым элементом второго списка.

Вот пример простого алгоритма с квадратичной сложностью, который ищет сумму всех пар элементов в массиве:

function sumOfPairs(arr) {     let sum = 0;     for (let i = 0; i < arr.length; i++) {         for (let j = 0; j < arr.length; j++) {             sum += arr[i] + arr[j];         }     }     return sum; } const myArray = [1, 2, 3, 4]; console.log(sumOfPairs(myArray)); // Результат: 40 

Этот код имеет два вложенных цикла, каждый из которых проходится по всему массиву. Количество операций в циклах равно n * n, где n - это длина массива. Это приводит к квадратичной сложности O(n^2), что может сделать его неэффективным для больших массивов из-за большого количества операций, выполняемых на каждый элемент.

Кубическая сложность O(n^3)

Cложность O(n^3) означает, что время выполнения алгоритма увеличивается кубически по размеру входных данных. Это часто встречается в алгоритмах, где есть три вложенных цикла или операции, каждая из которых выполняется пропорционально кубу размера входных данных.

Вот пример алгоритма с кубической сложностью, который умножает две матрицы:

function multiplyMatrices(matrix1, matrix2) {     let result = [];     const m = matrix1.length;     const n = matrix2[0].length;     const p = matrix2.length;      for (let i = 0; i < m; i++) {         result[i] = [];         for (let j = 0; j < n; j++) {             result[i][j] = 0;             for (let k = 0; k < p; k++) {                 result[i][j] += matrix1[i][k] * matrix2[k][j];             }         }     }     return result; }  const matrixA = [     [1, 2, 3],     [4, 5, 6],     [7, 8, 9] ];  const matrixB = [     [9, 8, 7],     [6, 5, 4],     [3, 2, 1] ];  console.log(multiplyMatrices(matrixA, matrixB));

Этот алгоритм умножения матриц имеет три вложенных цикла: первый проходится по строкам первой матрицы, второй по столбцам второй матрицы, а третий - по общим элементам для умножения. Количество операций равно n * n * n, где n - это размер матрицы. Это приводит к кубической сложности O(n^3). Такой подход может стать неэффективным для больших матриц из-за большого количества операций, которые необходимо.

Экспоненциальная сложность O(2^n)

Сложность O(2^n) относится к экспоненциальной сложности, где время выполнения алгоритма увеличивается экспоненциально по мере увеличения размера входных данных. Это часто встречается в алгоритмах, которые решают проблемы методом "разделяй и властвуй" или используют рекурсию без оптимизации.

Примером алгоритма с экспоненциальной сложностью может служить рекурсивное вычисление чисел Фибоначчи:

function fibonacci(n) {     if (n <= 1) {         return n;     } else {         return fibonacci(n - 1) + fibonacci(n - 2);     } } console.log(fibonacci(5)); // Результат: 5 console.log(fibonacci(10)); // Результат: 55 console.log(fibonacci(20)); // Результат: 6765

Этот код использует рекурсию для вычисления чисел Фибоначчи. Однако каждый раз, когда вызывается функция fibonacci, она порождает два дополнительных вызова, что приводит к экспоненциальному увеличению количества вызовов функций с увеличением n.

Для больших значений n такой подход становится очень неэффективным из-за огромного числа повторных вычислений. Экспоненциальная сложность обычно не является оптимальным решением из-за своей высокой вычислительной нагрузки при увеличении размера входных данных.

Факториальная сложность O(n!)

Сложность O(n!) относится к факториальной сложности, где время выполнения алгоритма растет пропорционально факториалу размера входных данных. Факториал - это произведение всех положительных целых чисел от 1 до n.

Пример алгоритма с факториальной сложностью может быть перебор всех перестановок элементов массива:

function permute(arr) {     function swap(a, b) {         const temp = arr[a];         arr[a] = arr[b];         arr[b] = temp;     }      function generate(n) {         if (n === 1) {             console.log(arr);         } else {             for (let i = 0; i < n - 1; i++) {                 generate(n - 1);                 if (n % 2 === 0) {                     swap(i, n - 1);                 } else {                     swap(0, n - 1);                 }             }             generate(n - 1);         }     }      generate(arr.length); }  const myArray = [1, 2, 3]; permute(myArray);

Этот код создает все возможные перестановки элементов массива путем рекурсивного генерирования всех возможных комбинаций. Количество операций, необходимых для генерации всех перестановок, равно факториалу длины массива. Например, для массива из 3 элементов (как в примере выше) будет 3! = 3 * 2 * 1 = 6 перестановок.

Такой алгоритм обладает очень высокой вычислительной сложностью и может стать практически неиспользуемым для больших входных данных из-за огромного числа операций, которые необходимо выполнить.

График сложностей алгоритмов

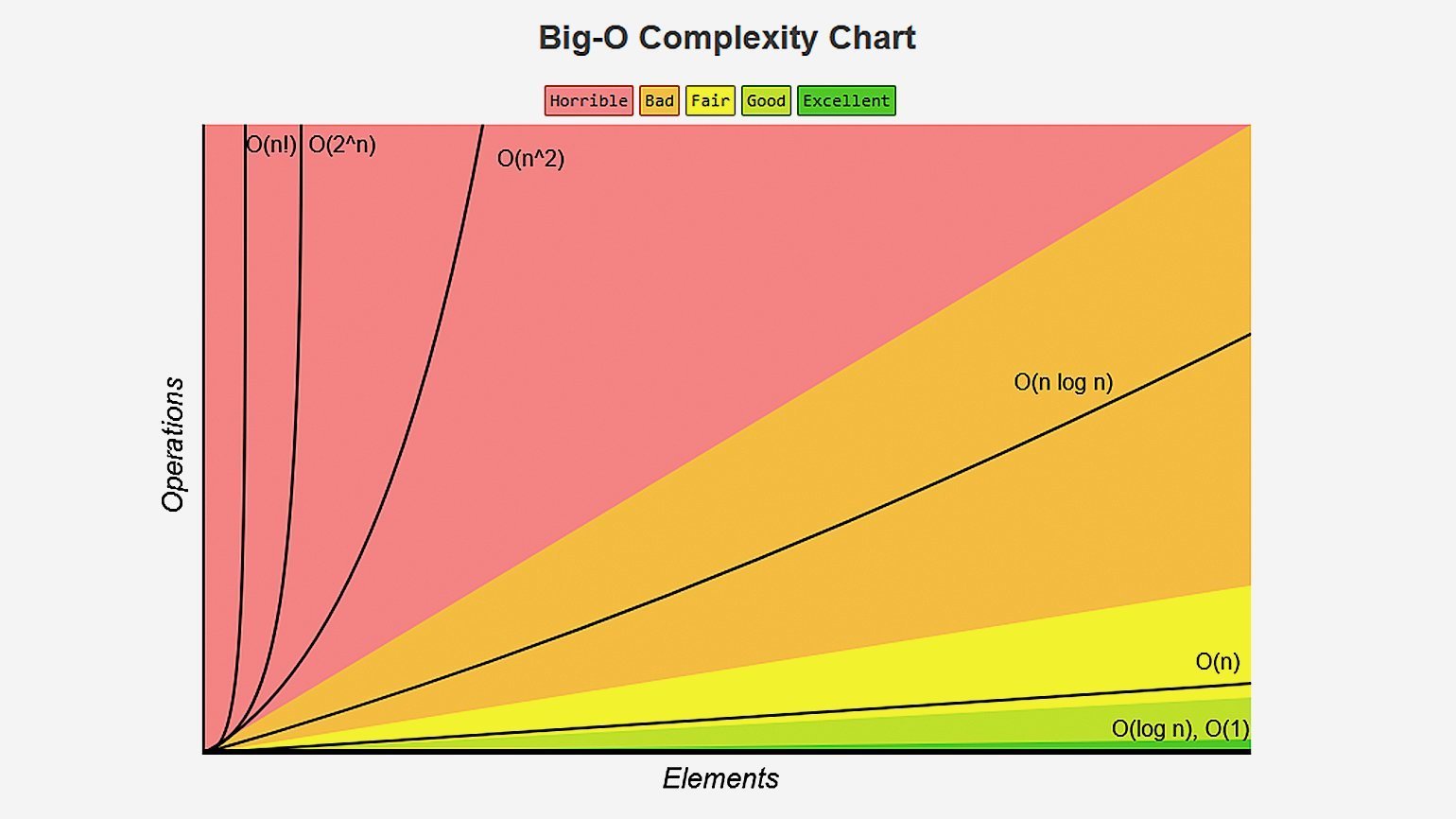
Посмотрите на этот график. На нем сразу видно различия между скоростью роста различных сложностей.

Отбрасывание констант и несущественной части

Big O указывает на самую быстро растущую сложность.

При оценке сложности алгоритмов часто игнорируются константы и несущественные части, так как они не оказывают значительного влияния на скорость роста времени выполнения алгоритма при увеличении размера входных данных. Это делается для получения более общего представления о росте сложности алгоритма.

Примеры:

Отбрасывание констант:

Пусть у нас есть алгоритм с временем выполнения 5n^2 + 3n + 2.

При оценке сложности по большому "O" отбрасываем константы и оставляем наиболее влиятельное слагаемое относительно размера входных данных, то есть O(n^2). Важно понимать, что при увеличении n, константы (3n, 2) и менее влиятельные части (3n, 2) становятся менее значимыми.

Отбрасывание несущественной части:

Рассмотрим алгоритм с временем выполнения O(n^2 + n + log n).

При оценке сложности по большому "O" отбрасываем менее влиятельные части и константы, оставляя самую значимую величину относительно размера входных данных, что приводит к O(n^2).

Использование такой асимптотической нотации позволяет увидеть, как алгоритм будет масштабироваться с ростом входных данных, игнорируя детали, не имеющие существенного влияния на его эффективность.

На практике это позволяет более удобно сравнивать алгоритмы и предсказывать их поведение при изменении размеров данных без учета точных числовых значений или мелких частей выражений, которые несущественны для скорости роста времени выполнения при увеличении n.

Примеры сокращений

Игнорирование констант:

// Сложность: O(2n) function printTwice(arr) {     for (let i = 0; i < 2 * arr.length; i++) {         console.log(arr[i]);     } } 

В данном случае, даже если у нас есть 2n операций, мы игнорируем константу 2 и получаем сложность O(n).

Отбрасывание несущественных частей:

// Сложность: O(n^2 + n + log n) function complexAlgorithm(n) {     for (let i = 0; i < n * n; i++) {         // ...некоторый код O(n^2)     }     for (let j = 0; j < n; j++) {         // ...некоторый код O(n)     }     for (let k = 2; k < n; k *= 2) {         // ...некоторый код O(log n)     } } 

В данном примере сложность алгоритма будет O(n^2), так как квадратичная часть (n^2) будет доминировать при увеличении n, в то время как линейная (n) и логарифмическая (log n) части станут несущественными.

Использование асимптотических оценок:

// Сложность: O(3n + 5) function simpleAlgorithm(arr) {     for (let i = 0; i < 3 * arr.length; i++) {         console.log(arr[i]);     }     for (let j = 0; j < 5; j++) {         console.log(j);     } } 

Здесь асимптотическая оценка сложности будет O(n), так как константы и несущественные части (в данном случае 5) игнорируются.

Сокращение выражений:

// Сложность: O(n^2 + 2n + 1) function exampleAlgo(n) {     for (let i = 0; i < n * n; i++) {         // ...некоторый код O(n^2)     }     for (let j = 0; j < 2 * n; j++) {         // ...некоторый код O(n)     }     console.log(1); // Операция O(1) } 

Здесь сложность алгоритма будет O(n^2), так как квадратичная часть (n^2) будет самой влиятельной при росте n.

Игнорирование меньших членов:

// Сложность: O(n^2 + n + 1000) function anotherAlgorithm(arr) {     for (let i = 0; i < arr.length * arr.length; i++) {         console.log(arr[i]);     }     for (let j = 0; j < arr.length; j++) {         console.log(j);     }     for (let k = 0; k < 1000; k++) {         console.log("Hi");     } } 

В данном примере, при увеличении размера n, слагаемые n и 1000 будут менее значимы, и сложность алгоритма будет определяться квадратичным членом, то есть O(n^2).

Эти примеры демонстрируют, как можно упрощать оценку сложности алгоритмов, игнорируя константы, несущественные части и фокусируясь на наиболее влиятельных компонентах при анализе поведения алгоритма на больших входных данных.

Упрощение арифметических выражений:

// Сложность: O(4n^2 + 3n + 10) function exampleFunc(n) {     for (let i = 0; i < 4 * n * n; i++) {         // ...некоторый код O(n^2)     }     for (let j = 0; j < 3 * n; j++) {         // ...некоторый код O(n)     }     console.log(10); // Операция O(1) } 

Здесь сложность оценивается как O(n^2), так как квадратичная часть (n^2) будет наиболее влиятельной при росте n.

Упрощение операций сравнения:

// Сложность: O(3n + n/2) function compareExample(arr) {     for (let i = 0; i < 3 * arr.length; i++) {         // ...некоторый код O(n)     }     for (let j = 0; j < arr.length / 2; j++) {         // ...некоторый код O(n/2)     } } 

Здесь, при упрощении, мы получим сложность O(n), так как в асимптотической оценке отбрасывается деление на константу.

Игнорирование доминирующего множителя:

// Сложность: O(1000n) function dominantMultiplier(arr) {     for (let i = 0; i < 1000 * arr.length; i++) {         // ...некоторый код O(n)     } }

Здесь, несмотря на присутствие множителя 1000n, сложность алгоритма все равно будет O(n), так как доминирующий множитель 1000 не влияет на общий характер роста при увеличении n.

Упрощение выражений с условиями:

// Сложность: O(n^2 + n) или O(n^2) function conditionalExample(arr) {     for (let i = 0; i < arr.length * arr.length; i++) {         if (i < arr.length) {             // ...некоторый код O(n)         }     } }

Здесь, при оценке сложности, условие i < arr.length также будет учтено как O(n), но влияние этого условия будет менее значимым при оценке сложности, и общая сложность останется O(n^2).

Эти примеры демонстрируют различные способы упрощения оценок сложности алгоритмов, учитывая различные аспекты вычислительной нагрузки и их влияние на общую скорость роста времени выполнения при увеличении размера входных данных.

Сложность встроенных методов JavaScript

Встроенные методы JavaScript обычно имеют свои собственные характеристики сложности, которые варьируются в зависимости от конкретного метода и типа данных, с которыми они работают. Вот несколько примеров:

Массивы:

• Добавление/удаление элемента в конце массива (например, push, pop): Сложность O(1). Эти операции работают быстро, так как не требуется сдвигать все элементы при добавлении или удалении элемента в начале массива.

• Добавление/удаление элемента в начале массива (например, unshift, shift): Сложность O(n). При добавлении или удалении элемента в начале массива требуется сдвиг всех остальных элементов.

• Доступ к элементу по индексу (например, arr[index]): Сложность O(1). Элементы массива обычно доступны напрямую по индексу, что делает эту операцию очень эффективной.

Строки:

• Слияние строк (например, использование + или concat): Сложность может быть O(n), так как при слиянии строк может потребоваться создание новой строки и копирование символов из оригинальных строк.

Объекты:

• Доступ к свойствам объекта (например, obj.prop): Обычно сложность доступа к свойствам объекта - O(1), но это может измениться в случае использования Map или WeakMap, где сложность доступа может быть ближе к O(log n) из-за особенностей реализации.

• Добавление/удаление свойств объекта: Обычно сложность добавления/удаления свойств в объекте - O(1).

Но важно понимать, что эти оценки сложности могут изменяться в зависимости от браузера, реализации JavaScript-движка и самого контекста использования. Также, некоторые операции могут иметь асимптотически более высокую сложность на больших данных, поэтому оценка сложности встроенных методов в JavaScript важна при проектировании эффективных алгоритмов.

Когда стоит обратить внимание на сложность алгоритмов:

1. Работа с большими объемами данных: Если ваше приложение работает с большими объемами данных (например, таблицы с тысячами строк, множество элементов на странице), неэффективные алгоритмы могут замедлить отклик приложения.

2. Частые вычисления в реальном времени: Если ваше приложение часто производит сложные вычисления в реальном времени (например, анимации, обработка данных пользовательского ввода), эффективные алгоритмы могут повысить отзывчивость интерфейса.

3. Операции сортировки, поиск и фильтрация: Если вам нужно часто выполнять операции сортировки, поиска или фильтрации в больших наборах данных на клиентской стороне, эффективные алгоритмы помогут улучшить производительность.

Когда можно не слишком беспокоиться о сложности алгоритмов:

1. Маленькие объемы данных и простые операции: В некоторых случаях, если ваше приложение работает с небольшим объемом данных и выполняет простые операции, вроде отображения небольших списков или форм, сложность алгоритмов может быть менее критичной.

2. Интерактивность: Если ваше приложение не требует сложных вычислений в реальном времени и предоставляет пользователю простые функции без длительного ожидания, удаление пристального внимания сложности алгоритмов может быть менее приоритетным.

Итак, важно учитывать контекст вашего приложения и его уникальные требования. Обычно начинать заботиться о сложности алгоритмов стоит, когда становится очевидным, что текущие алгоритмы или операции негативно влияют на производительность приложения или на его отзывчивость.

Пользуясь возможностью я хотел бы рассказать о своем YouTube канале Open JS посвященному Frontend-разработке. Буду рад подписке, лайкам и комментариям.

Спасибо за прочтение статьи до конца!