Восемь основных правил причинного вывода

В этом посте я опишу семь основных правил, которые регулируют взаимосвязь между причинно-следственными механизмами в реальном мире и ассоциациями/корреляциями, которые мы можем наблюдать в данных. Чтобы сделать каждое правило максимально простым для понимания, я опишу каждое правило как словами, так и в терминах причинно-следственной диаграммы и логики, а также предложу очень простой код моделирования R для каждого правила, чтобы продемонстрировать, как оно работает на практике.

Эти семь правил представляют собой основные строительные блоки причинного вывода. Большинство процедур причинно-следственного анализа в той или иной степени включают в себя одно или несколько из этих правил. Если вы совершенно не знакомы с формальным причинным выводом, изучение этих правил может послужить трамплином для изучения более сложных вещей. Если вы регулярно применяете причинно-следственные выводы в своих собственных исследованиях, этот пост может оказаться полезным в качестве шпаргалки. Гораздо более подробное введение в причинный вывод см. в Hern?n and Robins ( 2020 ) и в курсе Causal Diagrams от HarvardX.

Четыре фундаментальные причинные структуры

Причинно-следственный график — это изображение причинно-следственного механизма между переменными. На графике переменные (узлы) изображаются в виде кружков ? (или иногда в виде квадратов), а причинно-следственные связи (пути) между этими переменными изображаются в виде стрелок -> которые указывают от вызывающей вещи (причинного предка) к вызываемой вещи. (каузальный потомок).

Любой причинно-следственный график, каким бы сложным он ни был, можно разбить на четыре элементарных строительных блока. Блоки определяются типом пути, который можно проследить между переменными. Все правила, которые я опишу ниже, связаны с одним или несколькими из этих строительных блоков, поэтому полезно начать с их формулирования и описания. Поняв, с какими блоками мы работаем в каждом конкретном случае, мы узнаем, какие правила причинного вывода актуальны.

1. Полная независимость.

Между А и Б невозможно проследить путь.

2. Цепочка

В причинных цепочках можно проследить направленный путь от A до B, так что все стрелки указывают от A к B. Цепные пути иногда называют «открытым путем», что означает, что этот тип графа передает корреляцию между A и B ( см. правило 2). Когда цепочка включает три или более переменных, переменные M, связывающие A и B, часто называют медиаторами.

3. Вилка

В причинной развилке ненаправленный путь (не все стрелки идут в одном направлении) можно проследить от A до B через общего причинного предка C. C часто называют мешающей переменной. Разветвленные пути являются «открытыми» и передают корреляцию между A и B (см. правило 3).

4. Коллайдер

В причинном коллайдере ненаправленный путь (не все стрелки идут в одном направлении) можно проследить от A до B через причинного потомка D. D часто называют переменной коллайдера. Траектории коллайдера «замкнуты» и не передают корреляцию между A и B (см. правило 1).

Основные правила причинно-следственного вывода

Правило 1: Независимые переменные не коррелируют

Если A и B причинно независимы, они не будут связаны в данных.

Если тогда А ? Б.

# Rule 1 n=10000  # Number of data points a <- rnorm(n, 0, 1)  # A is a random variable b <- rnorm(n, 0, 1)  # B is a random variable plot(a, b)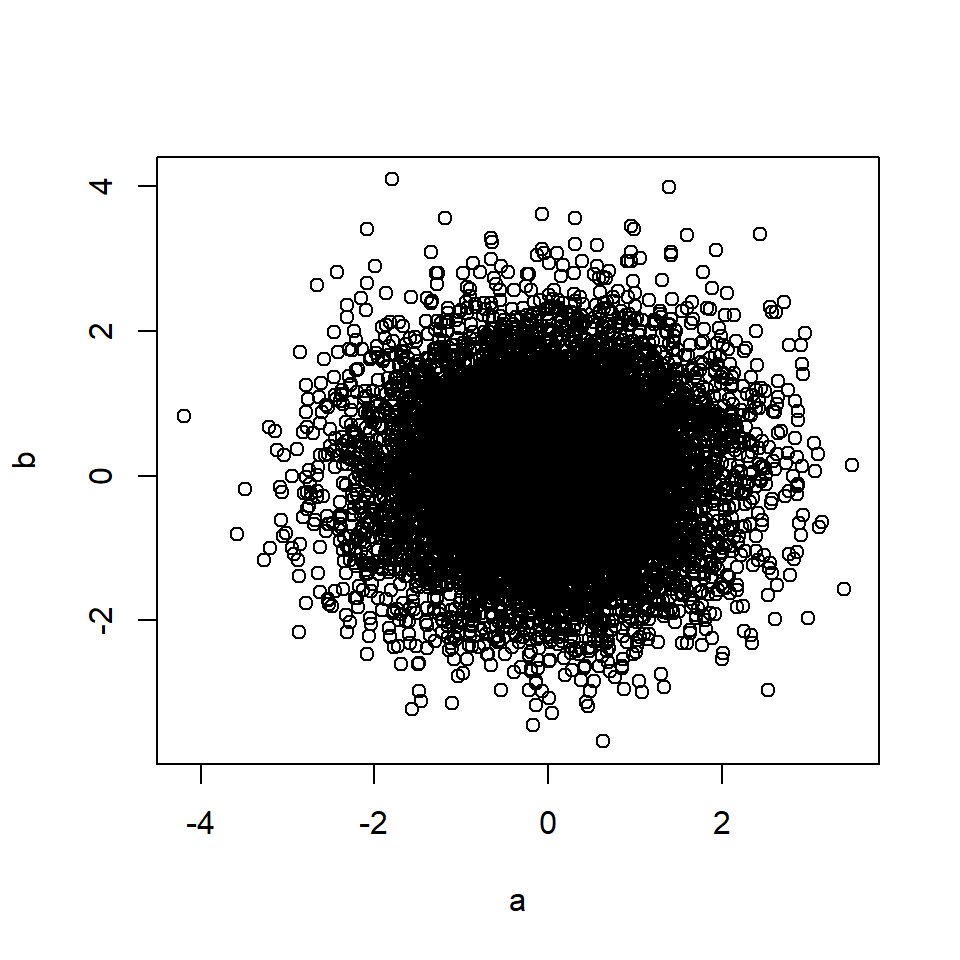  

cor(a, b)  # Correlation between A and B

## [1] 0.012

A и B каузально независимы, даже если у них общий причинный потомок (каузальный коллайдер), D. Две независимые причины общего потомка не коррелируют друг с другом (кроме правила 7).

Правило 2: Причинное влияние создает корреляцию

Если A является причиной B или если B является причиной A, то A и B будут коррелировать в данных.

Если или тогда А ~ В.

# Rule 2 n=10000  # Number of data points a <- rnorm(n, 0, 1)  # A is a random variable b <- a + rnorm(n, 0, 1)  # B is a function of A plot(a, b)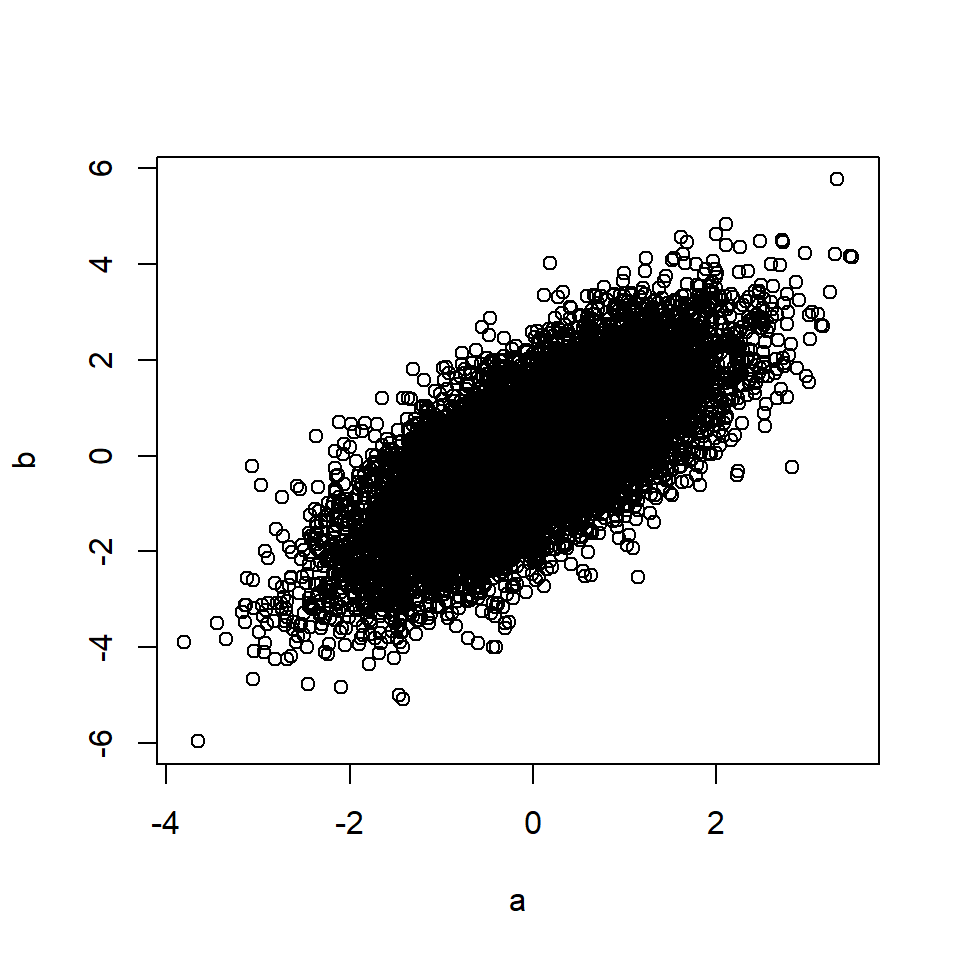  

cor(a, b)  # Correlation between A and B

## [1] 0.71

Это также применимо, если А вызывает М, а М, в свою очередь, вызывает Б (посредничество).

Если тогда А ~ В.

# Rule 2 (mediation) n=10000  # Number of data points a <- rnorm(n, 0, 1)  # A is a random variable m <- a + rnorm(n, 0, 1)  # M is a function of A b <- m + rnorm(n, 0, 1)  # B is a function of M plot(a, b)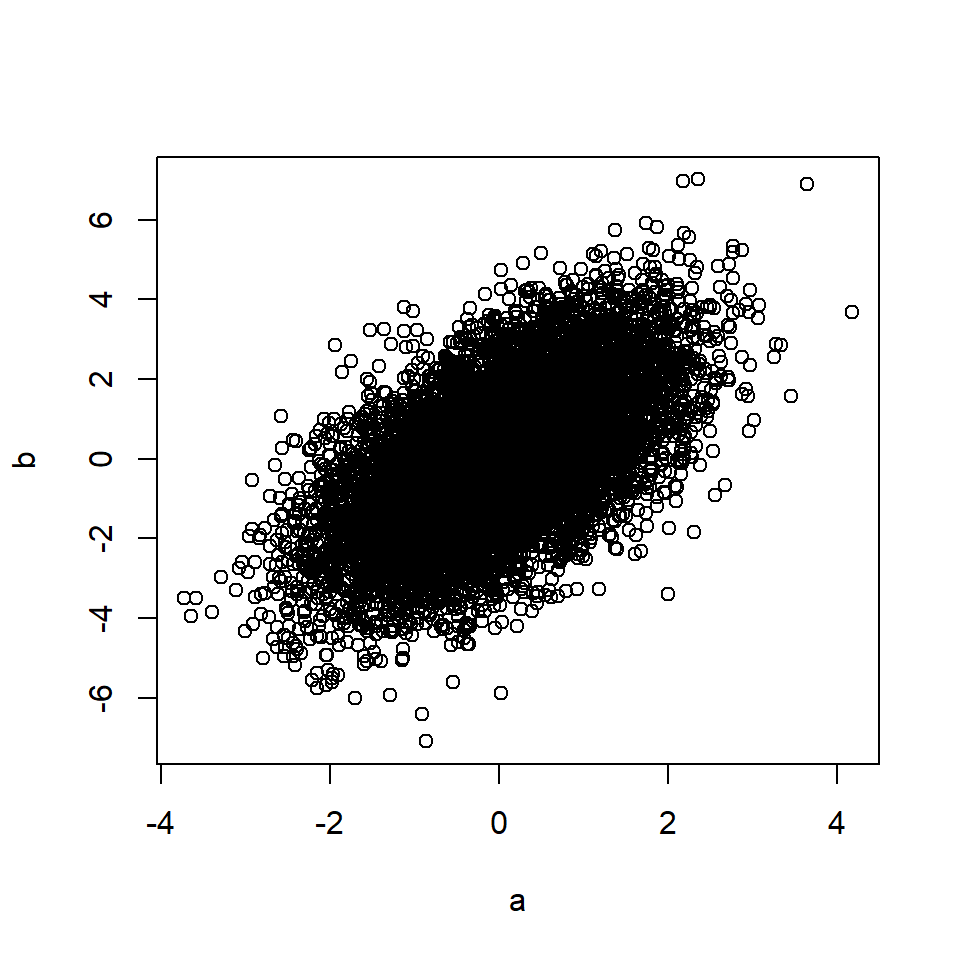  

cor(a, b)  # Correlation between A and B

## [1] 0.58

Правило 3: Смешение порождает корреляцию

Если A и B имеют общего предка C (причинная развилка), A и B будут коррелировать в данных. Это явление часто называют смешиванием или «проблемой третьей переменной».

Если тогда А ~ В.

# Rule 3 n=10000  # Number of data points c <- rnorm(n, 0, 1)  # C is a random variable a <- c + rnorm(n, 0, 1)  # A is a function of C b <- c + rnorm(n, 0, 1)  # B is a function of C plot(a, b)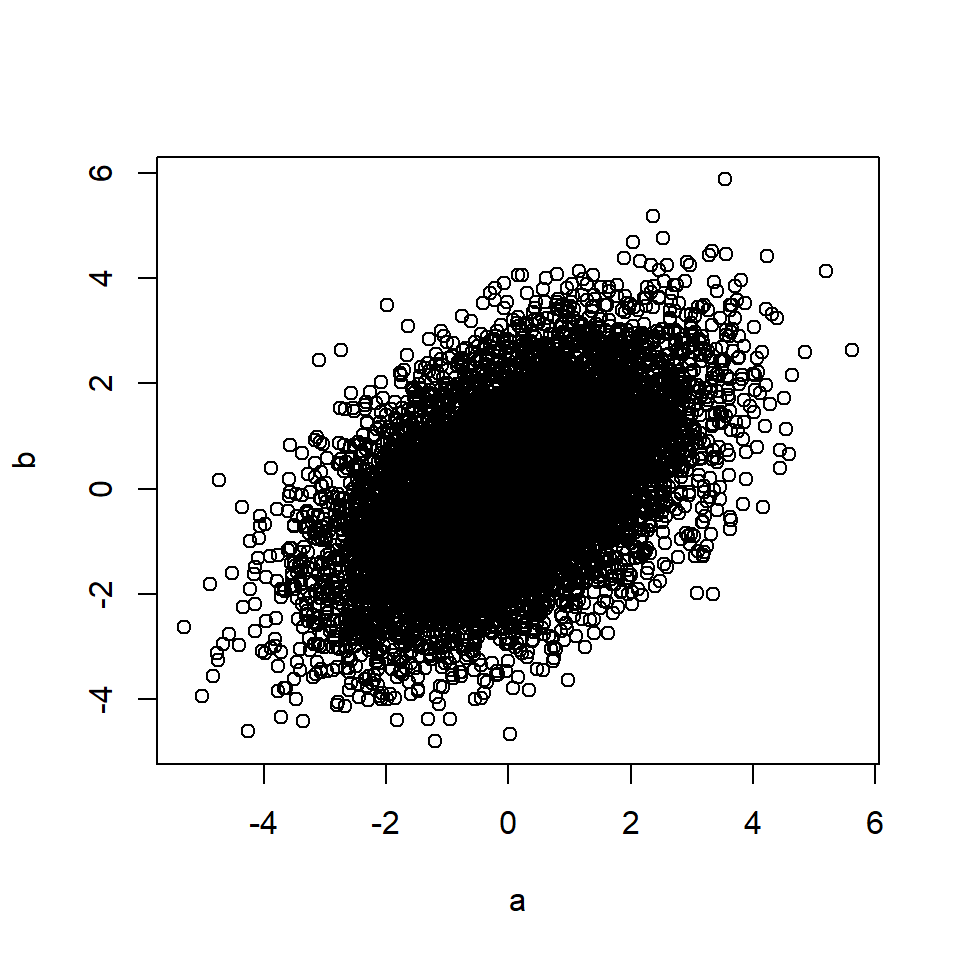  

cor(a, b)  # Correlation between A and B

## [1] 0.49

Правило также применяется, если влияние C на A и/или B опосредовано через другие переменные.

Правило 4: Случайное манипулирование защищает переменную от причинного влияния

Когда мы можем случайным образом распределить значения А — например, в рандомизированном контролируемом эксперименте, где А является переменной манипуляции, — никакая другая переменная не может влиять на А.

Обозначение do(A) относится к рандомизации значений A. Другими словами, при полном экспериментальном контроле и рандомизации мы гарантируем, что ни одна переменная не сможет влиять на значения A.

Правила настройки

Корректировка переменной X означает просмотр связей в данных, которые содержат только подмножество или одно значение X. Это также может означать просмотр связей для всех значений X отдельно. В науке корректировка имеет множество различных названий, включая «контроль», «условие включения», «сохранение константы», «расслоение», «выбор» и т. д.

На рисунках ниже квадратная рамка вокруг узла переменной указывает, что эта переменная контролируется/настраивается.

Правило 5: Контроль искажающего фактора блокирует корреляцию, возникающую из-за этого искажающего фактора.

Если A и B имеют общего предка C (причинная развилка), искажающая корреляция между A и B, созданная C (правило 3), удаляется, если C находится под контролем.

Если тогда А ? Б.

# Rule 5 n=10000  # Number of data points c <- rnorm(n, 0, 1)  # C is a random variable a <- c + rnorm(n, 0, 1)  # A is a function of C b <- c + rnorm(n, 0, 1)  # B is a function of C x <- lm(b~c) y <- lm(a~c) plot(x$residuals, y$residuals)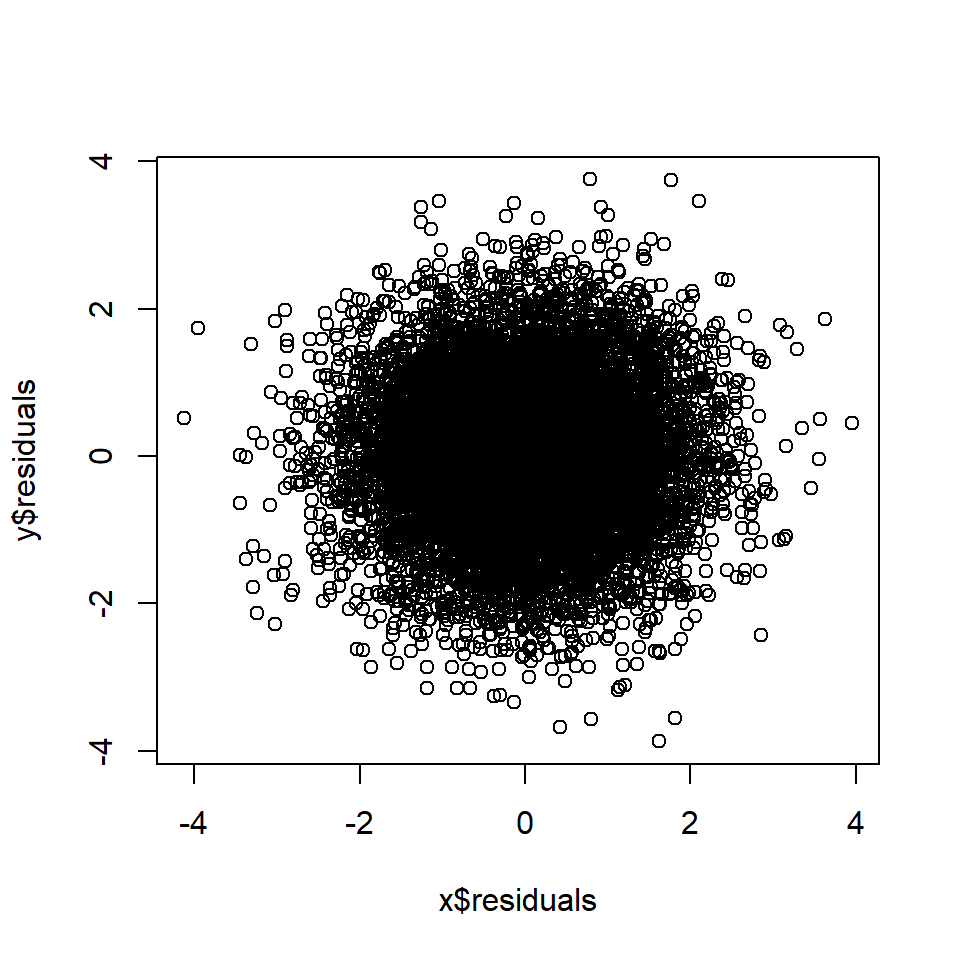 

cor(x$residuals, y$residuals)  # Correlation between A and B, controlling for C

## [1] 0.015

Правило 6. Контроль посредника блокирует корреляцию, возникающую в результате опосредованного причинного эффекта.

Если А является причиной М, а М является причиной В, то корреляция между А и В, созданная опосредованным причинным следствием (правило 2), будет устранена, если М будет контролироваться.

Если тогда А ? Б.

# Rule 6 n=10000  # Number of data points a <- rnorm(n, 0, 1)  # A is a random variable m <- a + rnorm(n, 0, 1)  # M is a function of A b <- m + rnorm(n, 0, 1)  # B is a function of M x <- lm(a~m) y <- lm(b~m) plot(x$residuals, y$residuals)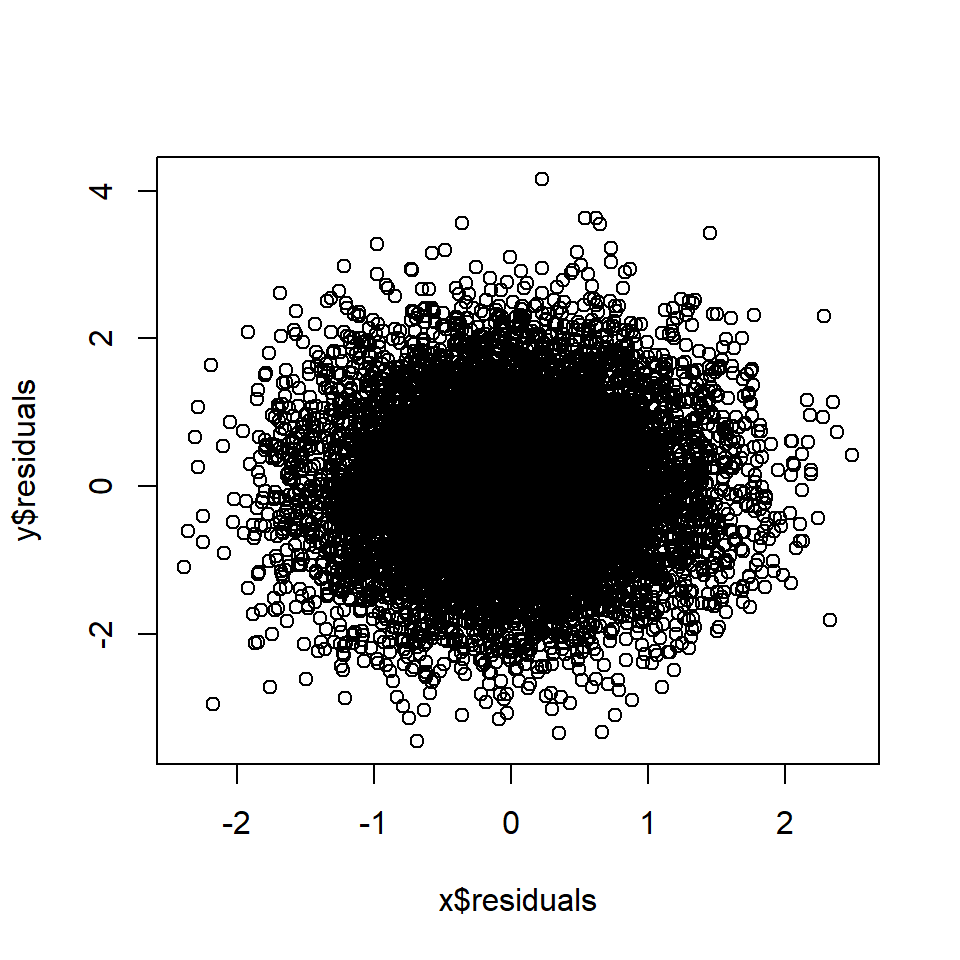 

cor(x$residuals, y$residuals)  # Correlation between A and B, controlling for M

## [1] 0.027

Правило 7: Контроль коллайдера приводит к корреляции

Если A и B имеют общего причинного потомка (коллайдер) D и D контролируется, A и B станут коррелированными в данных. Это часто называют «кондиционированием на коллайдере» или смещением коллайдера.

Если тогда А ~ В.

# Rule 7 n=10000  # Number of data points a <- rnorm(n, 0, 1)  # A is a random variable b <- rnorm(n, 0, 1)  # B is a random variable d <- a + b + rnorm(n, 0, 1)  # D is a function of A and B x <- lm(a~d) y <- lm(b~d) plot(x$residuals, y$residuals)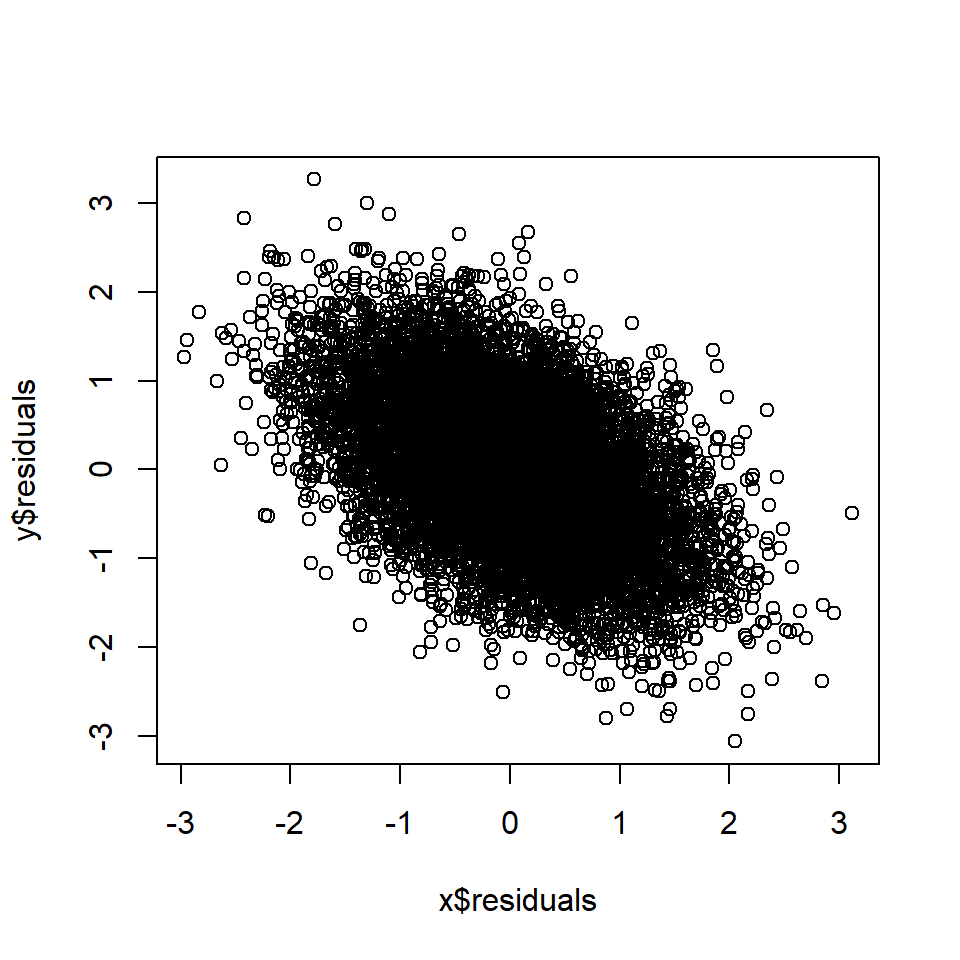 

cor(x$residuals, y$residuals)  # Correlation between A and B, controlling for D

## [1] -0.5

Правило 8: Контроль причинного потомка (частично) контролирует предка

Если B является потомком A и B находится под контролем, то A также (частично) контролируется.

Степень, в которой контролируется А, когда контролируется Б, обычно зависит от того, насколько надежно А вызывает Б.

В приведенном ниже примере C смешивает A и B, но мешающее влияние можно частично заблокировать, контролируя CM.

Если CM является полунадежной мерой C, некоторая корреляция между A и B устраняется при контроле CM, но не в такой степени, как при контроле C:

# Rule 5 n=10000  # Number of data points # 2*c used in equations to make change in relationship more visible. c <- rnorm(n, 0, 1)  # C is a random variable a <- 2*c + rnorm(n, 0, 1)  # A is a function of C b <- 2*c + rnorm(n, 0, 1)  # B is a function of C cm <- 2*c + rnorm(n, 0, 1) # CM is a function of C # Control for C ac <- lm(b~c) bc <- lm(a~c) # Control for CM acm <- lm(a~cm) bcm <- lm(b~cm) # Plot relationship between a and b while... par(mfrow=c(1,3))  plot(a,b, main = "no control")  # controlling for nothing plot(acm$residuals, bcm$residuals, main = "controlling for CM")  # controlling for CM plot(ac$residuals, bc$residuals, main = "controlling for C")  # controlling for C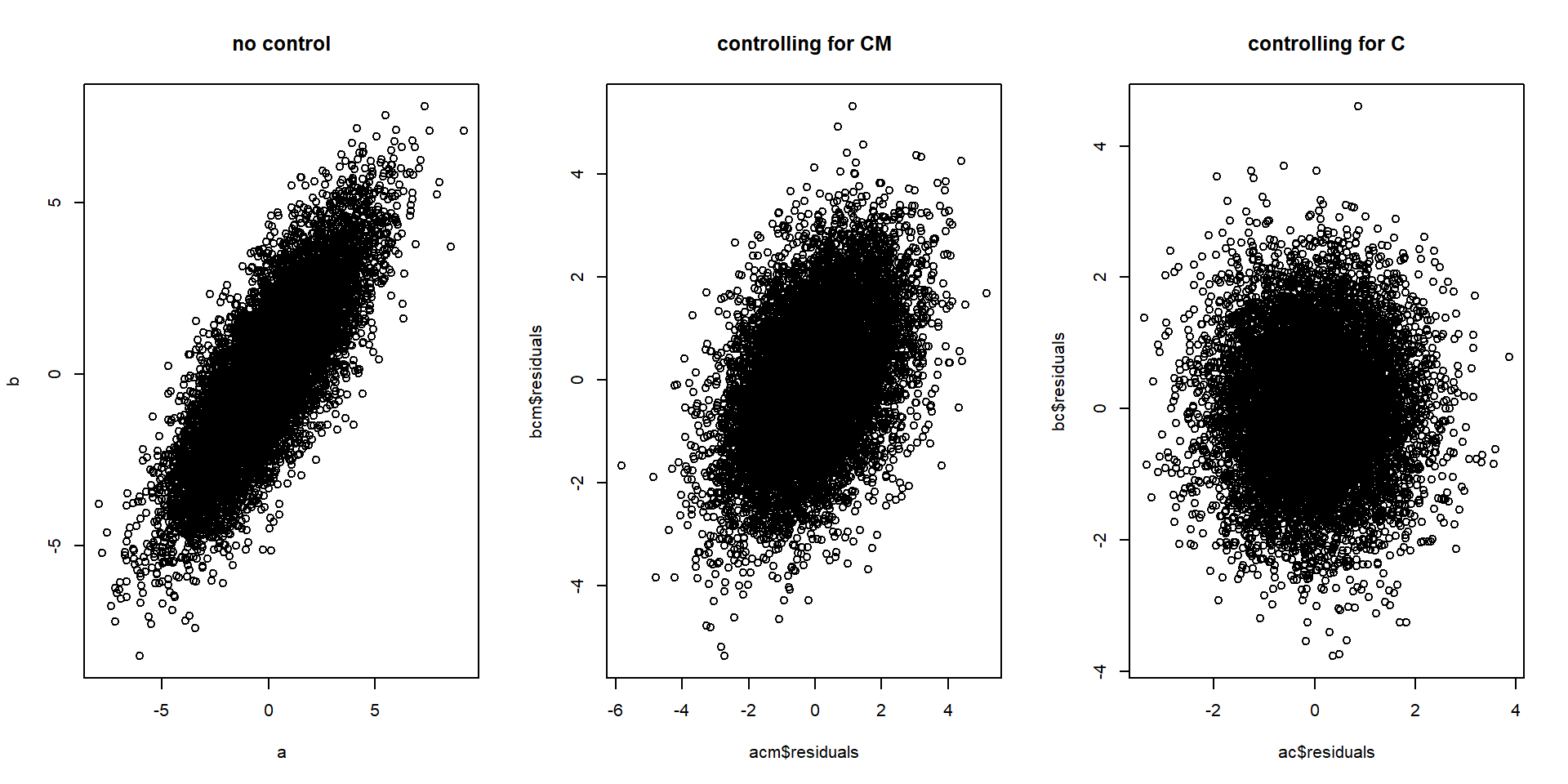

# Correlation between a and b while... cor(a,b) # controlling for nothing

## [1] 0.8

cor(acm$residuals, bcm$residuals)  # controlling for CM

## [1] 0.44

cor(ac$residuals, bc$residuals)  # controlling for C

## [1] 0.0021

Примечание. Коррелированность не обязательно означает линейную корреляцию.

В этом тексте я часто использую термин «коррелированный». Для многих термин корреляция является синонимом линейной корреляции. Однако я имею в виду не это . Здесь «корреляция» просто означает «взаимосвязь», «ассоциацию» или «взаимную информацию». Если А и Б коррелируют, это просто означает, что что-то систематически происходит с Б, когда что-то происходит с А.

Например, правило 2 не подразумевает, что A и B будут находиться в линейной корреляции, когда A вызывает B; просто B будет каким-то образом систематически меняться при изменении A.

Для простоты я использовал линейные корреляции во всех примерах кода R. Однако в реальной жизни ожидаемая нами картина корреляции/ассоциации/взаимной информации полностью зависит от функциональной формы задействованных причинных связей.

Важные предположения

Вышеупомянутые правила справедливы только в том случае, если выполняются некоторые важные предположения, которые я перечислю ниже, но не буду объяснять подробно. Подробнее см. Hern?n and Robins ( 2020 ) .

Отсутствие ложной корреляции: корреляция не вызвана случайностью. Закон больших чисел гласит: чем больше у нас данных, тем более правдоподобным является это предположение.

Согласованность: значения A, которые вы видите, являются фактическими значениями A, или «значения сравниваемого лечения соответствуют четко определенным вмешательствам, которые, в свою очередь, соответствуют вариантам лечения в данных» Эрнан и Робинс ( 2020 ). .

Заменяемость: «условная вероятность получения каждого значения лечения, хотя и не определена исследователями, зависит только от измеренных ковариат» Эрнан и Робинс ( 2020 ) .

Позитивность: «вероятность получения любого значения лечения, обусловленного L, больше нуля, т. е. положительна» Эрнан и Робинс ( 2020 ) .

Достоверность: Причинно-следственный эффект не варьируется в зависимости от группы таким образом, чтобы его среднее значение в данных было равно 0. А не оказывает положительного эффекта в 50% случаев и столь же мощного отрицательного эффекта в 50% случаев, что в среднем равно 0 в популяции.

Если какое-либо из этих предположений не выполняется, это потенциально может нарушить связь между причинным эффектом и наблюдаемыми данными, описанными этими правилами.

Источник: pedermisager-org.translate.goog

Комментарии: