Почему в Data Science не обойтись без математики
Все ключевые аспекты Data Science неразрывно связаны с математикой, поскольку она предоставляет фундаментальную основу и все необходимые инструменты для понимания, анализа и интерпретации информации:
- Анализ данных – для понимания и интерпретации информации используются математическая статистика, линейная алгебра и теория вероятностей.
- Понимание взаимосвязей – для выявления, количественной оценки и моделирования различных типов взаимосвязей в данных (от простых линейных зависимостей до сложных нелинейных и многомерных отношений) применяются математическая статистика, линейная алгебра, теория вероятностей, теория графов, функциональный анализ, персистентная гомология.
- Разработка алгоритмов – алгоритмы машинного обучения основаны на определенных математических концепциях. Понимание этих концепций позволяет специалистам по Data Science выбирать, адаптировать и оптимизировать алгоритмы для конкретных задач.
- Оценка моделей – математические методы используются для оценки производительности моделей машинного обучения и определения их эффективности.
- Обработка больших объемов данных – математические методы помогают эффективно обрабатывать и анализировать большие массивы данных.
- Визуализация данных – математические концепции лежат в основе многих методов визуализации данных, помогая эффективно представлять сложную информацию.
- Прогнозирование – математические модели используются для создания точных прогнозов на основе исторических данных.
- Решение оптимизационных задач – многие задачи в Data Science связаны с оптимизацией, которая напрямую опирается на математические методы.
- Понимание ограничений – знание математики помогает специалистам по Data Science лучше понимать ограничения и допущения используемых методов и моделей.
- Инновации – глубокое понимание математики позволяет создавать новые алгоритмы и методы анализа данных, способствуя развитию области.
Какие разделы математики нужно знать для работы в Data Science
Важно заметить, что глубина необходимых знаний в той или иной области математики варьируется в зависимости от конкретной специализации в Data Science. Но в целом, абсолютно необходимый минимум сводится к перечисленным ниже ключевым разделам.
1. Базовые математические концепции и математический анализ
Теория чисел
- Применяется в алгоритмах хеширования, которые важны для эффективного хранения и поиска данных.
- Помогает в понимании и оптимизации вычислительных алгоритмов.
Порядок операций
- Критически важен для правильного написания и интерпретации математических выражений в коде.
- Обеспечивает корректность вычислений в сложных формулах и алгоритмах.
my_value = 2 * (3 + 2)**2 / 5 - 4 print(my_value) # Вывод: 6.0 Переменные
- Основа программирования и моделирования в Data Science.
- Используются для представления признаков, параметров моделей и промежуточных результатов вычислений.
Функции
- Используются во всех аспектах науки о данных – от сбора, обработки, анализа и визуализации информации до оценки и оптимизации моделей.
Пример – визуализация функции в трехмерном пространстве:
from sympy import symbols from sympy.plotting import plot3d x, y = symbols('x y') f = 2*x + 3*y plot3d(f) 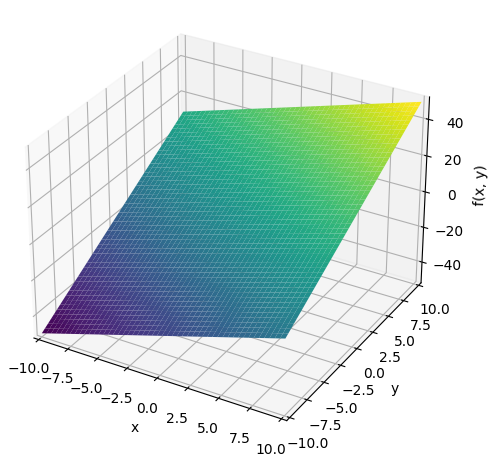
Суммирование
- Используется в вычислении агрегированных метрик (например, суммы квадратов ошибок).
- Применяется в алгоритмах машинного обучения.
summation = sum(2 * i for i in range(1, 6)) print(summation) # Вывод: 30 Экспоненты
- Применяются в масштабировании данных, особенно для признаков с большим разбросом значений.
- Используются в некоторых активационных функциях нейронных сетей (например, ELU).
- Важны в моделировании экспоненциального роста или спада.
Логарифмы
- Часто применяются для нормализации данных с большим разбросом значений.
- Используются в информационной теории (например, энтропия в деревьях решений).
- Помогают в визуализации данных с большим диапазоном значений.
Пример – использование логарифма для определения степени:
from math import log # 2 в какой степени равно 8? x = log(8, 2) print(x) # Вывод: 3.0 Число Эйлера и натуральные логарифмы
- Широко используются в статистическом моделировании.
- Применяются в логистической регрессии и других вероятностных моделях.
- Важны в оптимизации и максимизации функций правдоподобия.
Пример – вычисление непрерывного процента:
from math import exp p = 100 # Начальная сумма r = .20 # Годовая процентная ставка t = 2.0 # Время в годах a = p * exp(r*t) print(a) # Вывод: 149.18246976412703 Пределы
- Помогают понять поведение функций и алгоритмов при стремлении параметров к определенным значениям.
- Используются в анализе сходимости алгоритмов машинного обучения.
Пример – вычисление предела, который определяет число e:
from sympy import symbols, limit, oo n = symbols('n') f = (1 + (1/n))**n result = limit(f, n, oo) print(result) # E print(result.evalf()) # Вывод: 2.71828182845905 Производные
- Ключевой компонент в оптимизации моделей машинного обучения, особенно в градиентном спуске.
- Применяются для нахождения локальных минимумов и максимумов функций потерь.
- Используются в анализе чувствительности моделей к изменениям входных параметров.
Частные производные
- Применяются в многомерной оптимизации, например, в нейронных сетях.
- Используются для вычисления градиентов в алгоритмах обучения.
Пример – вычисление и визуализация частных производных:
from sympy import symbols, diff from sympy.plotting import plot3d x, y = symbols('x y') f = 2*x**3 + 3*y**3 # Вычисляем частные производные по x и y dx_f = diff(f, x) dy_f = diff(f, y) print(dx_f) # Вывод: 6*x**2 print(dy_f) # Вывод: 9*y**2 plot3d(f) 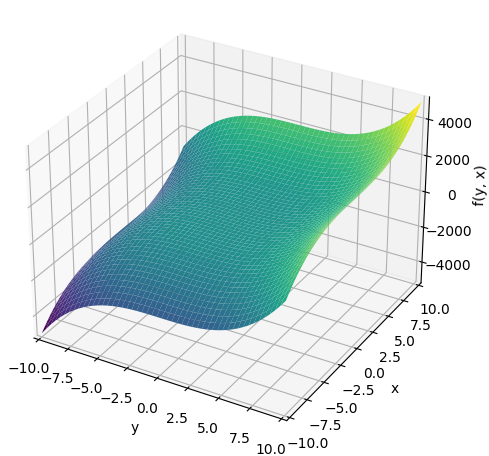
Цепное правило
- Важно для понимания и реализации алгоритма обратного распространения ошибки в нейронных сетях.
- Применяется при вычислении градиентов сложных композитных функций.
Интегралы
- Используются в вероятностном моделировании и статистическом выводе.
- Применяются в вычислении площадей под кривыми распределения вероятностей.
- Важны в некоторых методах оценки плотности вероятности.
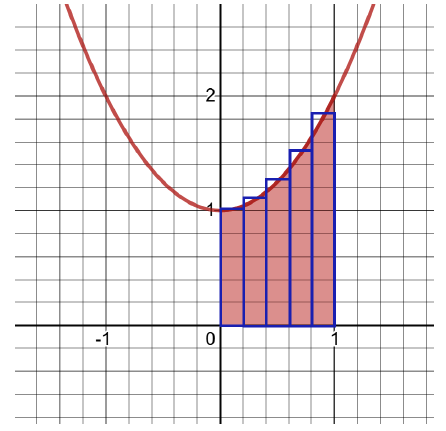
def approximate_integral(a, b, n, f): delta_x = (b - a) / n total_sum = 0 for i in range(1, n + 1): midpoint = 0.5 * (2 * a + delta_x * (2 * i - 1)) total_sum += f(midpoint) return total_sum * delta_x def my_function(x): return x**2 + 1 area = approximate_integral(a=0, b=1, n=5, f=my_function) print(area) # Вывод: 1.33 Библиотека Дата Сайентиста
Больше полезных материалов вы найдете на нашем телеграм-канале «Библиотека Дата Сайентиста»
Библиотека DS для собеса
Подтянуть свои знания по DS вы можете на нашем телеграм-канале «Библиотека DS для собеса»
Библиотека задач по DS
Интересные задачи по DS для практики можно найти на нашем телеграм-канале «Библиотека задач по DS»
2. Теория вероятностей
Вероятность – основа статистического вывода и многих алгоритмов машинного обучения. Понимание вероятности критично для интерпретации результатов моделей и оценки неопределенности:
- Совместные вероятности используются в анализе многомерных данных и в построении байесовских сетей.
- Условная вероятность – основа для байесовских методов машинного обучения, включая наивный байесовский классификатор.
- Биномиальное распределение применяется в моделировании бинарных исходов, например, в A/B тестировании.
- Бета-распределение часто используется как априорное распределение в байесовском выводе.
Пример – вычисление и визуализация биномиального распределения:
import matplotlib.pyplot as plt from scipy.stats import binom n = 10 p = 0.9 k_values = list(range(n + 1)) probabilities = [binom.pmf(k, n, p) for k in k_values] plt.bar(k_values, probabilities, color='blue') plt.xlabel('k исходов (10 испытаний)') plt.ylabel('Вероятность') plt.title('Биномиальное распределение (n=10, p=0.9)') plt.ylim(0, 0.4) plt.grid(True, which='both', axis='y', color='gray', linestyle='--', linewidth=0.5) plt.show() 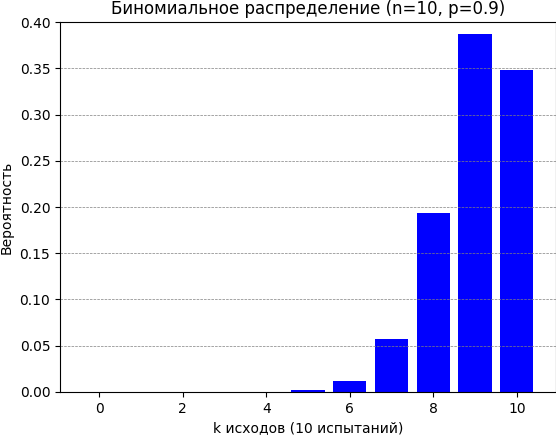
Статья по теме
Теория вероятностей: где она используется и нужна ли она рядовому разработчику
3. Описательная и выводная статистика
Это важнейшие инструменты для понимания и интерпретации данных:
- Описательная статистика (среднее, медиана, мода, дисперсия, стандартное отклонение) используется для суммирования характеристик данных.
- Нормальное распределение – многие статистические методы основаны на предположении о нормальности данных.
- Обратная функция распределения используется в генерации случайных чисел и в квантильной регрессии.
- Z-оценки применяются для стандартизации данных и выявления выбросов.
- Центральная предельная теорема обосновывает применение многих статистических методов к реальным данным.
- Доверительные интервалы используются для оценки неопределенности в статистических выводах.
- P-значения – ключевой инструмент в проверке статистических гипотез.
- T-распределение применяется при работе с малыми выборками.
4. Линейная алгебра
Линейная алгебра предоставляет эффективные инструменты для работы с многомерными данными:
- Векторы и матрицы используются для эффективного представления и манипулирования данными.
- Линейные преобразования применяются в обработке изображений и в некоторых методах машинного обучения.
- Умножение матриц – ключевая операция во многих алгоритмах, включая нейронные сети.
- Определители используются в решении систем линейных уравнений и в некоторых методах классификации.
- Обратные матрицы применяются в решении систем линейных уравнений, которые используются во многих алгоритмах машинного обучения.
- Собственные векторы и собственные значения используются в методах снижения размерности (например, в методе главных компонент), и в некоторых алгоритмах кластеризации.
Предположим, у нас есть вектор v:
И вектор w:
Так выглядит математическая операция сложения:
А так операция сложения производится в Python (с помощью NumPy):
from numpy import array v = array([3, 2]) w = array([2, -1]) v_plus_w = v + w print(v_plus_w) #Вывод: [5 1] 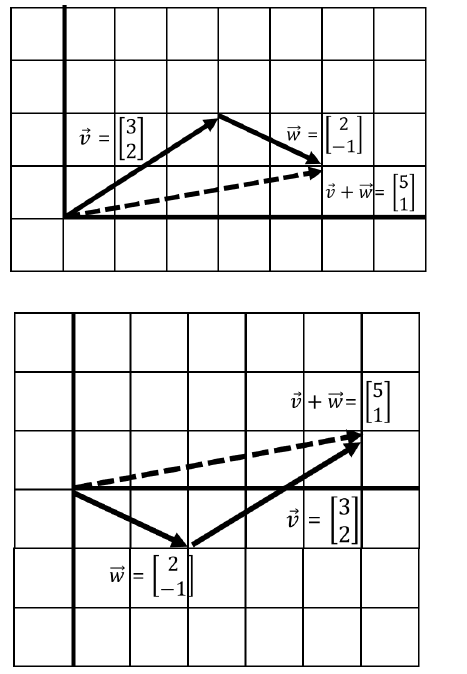
5. Линейная регрессия
Линейная регрессия – это фундаментальный метод прогнозирования в статистике и машинном обучении. Основные математические концепции, связанные с линейной регрессией:
- Метод наименьших квадратов – основной способ оценки параметров в линейной регрессии.
- Градиентный спуск – итеративный метод оптимизации, широко используемый в машинном обучении.
- Стохастический градиентный спуск – эффективный метод оптимизации для больших наборов данных.
- Коэффициент корреляции используется для оценки силы линейной связи между переменными.
- Коэффициент детерминации (R-квадрат) – мера качества подгонки модели.
- Доверительные интервалы предсказания используются для оценки неопределенности прогнозов.
Статья по теме
Как линейная алгебра используется в машинном обучении?
6. Логистическая регрессия и классификация
Логистическая регрессия – это метод, который помогает предсказать, произойдет какое-то событие или нет. Например, купит ли клиент товар, заболеет ли пациент, будет ли дождь и т.д.
Логистическая регрессия работает так:
- Берет разные характеристики (признаки) и комбинирует их.
- Затем преобразует результат в число от 0 до 1.
- Это число можно интерпретировать как вероятность события.
Предположим, мы хотим предсказать, купит ли человек машину. Мы учитываем его возраст, доход и наличие семьи. Логистическая регрессия возьмет эти данные и выдаст вероятность покупки. Кроме того, логистическая регрессия часто используется для бинарной классификации: она дает вероятность принадлежности к классу, которую можно преобразовать в конкретное решение (например, если вероятность > 0.5, то относим к классу 1, иначе к классу 0).
Эта функция показывает, как логистическая регрессия преобразует линейную комбинацию признаков (b0 + b1 * x) в вероятность, которая всегда находится в диапазоне от 0 до 1:
from sympy import symbols, exp, plot b0, b1, x = symbols('b0 b1 x') p = 1.0 / (1.0 + exp(-(b0 + b1 * x))) p = p.subs({b0: -2.823, b1: 0.620}) print(p) plot(p) 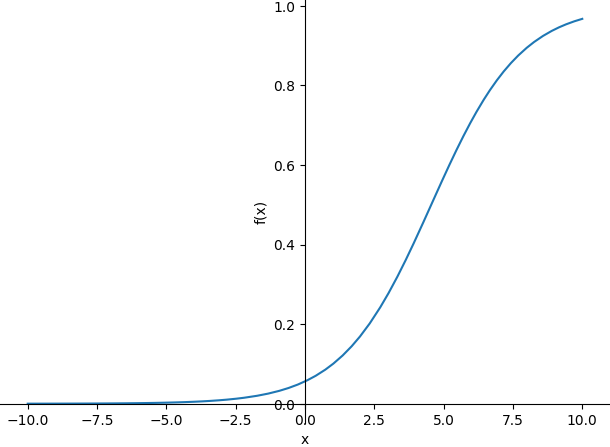
7. Нейронные сети
Нейронные сети – мощный инструмент для анализа больших объемов данных, выявления скрытых закономерностей и принятия решений. Все основные концепции, которые нужно знать для создания и использования нейронок, имеют математическую основу:
- Архитектуры нейронных сетей опираются на линейную алгебру и теорию графов.
- Нормализация данных использует статистические методы.
- Кросс-валидация основана на статистических принципах.
- Функции активации определяют нелинейность модели. Чаще всего используют линейный выпрямитель ReLU, логистическую функцию и гиперболический тангенс.
- Прямое распространение – процесс вычисления выхода сети на основе входных данных.
- Обратное распространение ошибки – алгоритм для эффективного вычисления градиентов в многослойных сетях.
- Стохастический градиентный спуск – основной метод оптимизации параметров нейронных сетей.
- Функции потерь основаны на математической статистике и теории оптимизации.
- Регуляризация (особенно L1 и L2) использует концепции из линейной алгебры и оптимизации.
- Методы инициализации весов основаны на теории вероятностей и статистике.
- Оптимизаторы основаны на математических методах оптимизации.
- Метрики производительности основаны на статистике.
Подведем итоги
Итак, для успешной работы в Data Science нужно знать:
- Базовые математические концепции и математический анализ.
- Теорию вероятностей.
- Описательную и выводную статистику.
- Линейную алгебру.
- Линейную и логистическую регрессию.
- Основы нейронных сетей.
Увереное владение этими математическими концепциями позволяет специалистам по Data Science:
- Глубже понимать алгоритмы и методы анализа данных.
- Эффективно обрабатывать и интерпретировать большие объемы информации.
- Разрабатывать и оптимизировать модели машинного обучения.
- Оценивать эффективность и ограничения используемых методов.
- Создавать инновационные решения в области анализа данных.
Важно отметить, что всю необходимую математическую базу можно освоить самостоятельно, если не торопиться и подходить к изучению системно. Для тех, кто стремится ускорить процесс обучения, есть специализированные курсы, которые помогут быстрее овладеть нужными навыками.
Другой важный момент заключается в том, что Data Science постоянно развивается, и в некоторых нишах могут потребоваться особые, более углубленные математические навыки. Например, в сфере компьютерного зрения нужноуглубленное знание геометрии, а в области обработки естественного языка – продвинутые статистические методы. Поэтому дата-сайентистам необходимо непрерывно развиваться, следить за новыми тенденциями и быть готовыми осваивать дополнительные математические концепции по мере необходимости.
***
Онлайн-курс по математике для Data Science от Proglib Academy
Если вы хотите углубить свои знания в Data Science и стать востребованным специалистом, вам необходима прочная математическая база. Наш онлайн-курс по математике для Data Science поможет вам освоить все ключевые концепции и методы.
Что вы получите на курсе
- Теория вероятностей:Основы и применение для анализа данных и машинного обучения.
- Линейная алгебра:Векторы, матрицы, собственные значения и их использование в Data Science.
- Математический анализ:Пределы, производные, интегралы и их применение в оптимизации моделей.
- Комбинаторика:Правила, множества и сочетания.
- Основы машинного обучения:Word2vrc, случайный лес, KNN, байесовский классификатор.
Интересно, хочу попробовать
