Уменьшение размерности: PCA, tSNE, UMAP

Зачем уменьшать размерность?

Снижение размерности — это метод, используемый в машинном обучении и анализе данных для уменьшения количества входных переменных или функций в наборе данных при сохранении наиболее важной информации. Этот процесс включает в себя преобразование многомерных данных в пространство более низкой размерности, где каждое измерение представляет собой комбинацию исходных функций.

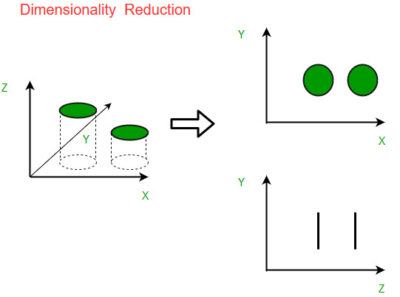
Основная цель уменьшения размерности — упростить набор данных за счет устранения избыточных или ненужных функций, что может привести к нескольким преимуществам:

1. Вычислительная эффективность: обработка и анализ многомерных данных может оказаться дорогостоящим в вычислительном отношении. За счет уменьшения размерности можно значительно снизить сложность вычислений, сделав алгоритмы более эффективными.
2. Снижение шума. Снижение размерности может помочь отфильтровать шумные или ненужные функции, которые могут отрицательно повлиять на производительность моделей машинного обучения. Сосредоточив внимание на наиболее информативных аспектах, модели могут обеспечить лучшее обобщение и точность прогнозирования.
3. Визуализация. Визуализация многомерных данных является сложной задачей, поскольку люди могут напрямую воспринимать только до трех измерений. Методы уменьшения размерности позволяют представлять данные в двух или трех измерениях, что упрощает визуализацию и интерпретацию.
4. Разработка объектов. Уменьшение размерности может помочь в разработке объектов за счет создания новых производных объектов, которые собирают наиболее важную информацию в исходном наборе данных. Эти производные функции затем можно использовать в качестве входных данных для последующих моделей машинного обучения.

Существует два основных подхода к уменьшению размерности:

1. Выбор функций. Этот подход предполагает выбор подмножества исходных функций на основе определенных критериев, таких как статистические тесты, корреляционный анализ или знание предметной области. Выбранные функции сохраняются, а остальные отбрасываются.
2. Извлечение функций. При этом подходе новые функции создаются путем объединения или преобразования исходных функций. Цель состоит в том, чтобы найти представление меньшей размерности, которое сохранит наиболее важную информацию из исходных данных. Для извлечения признаков обычно используются такие методы, как анализ главных компонентов (PCA), линейный дискриминантный анализ (LDA) и t-распределенное стохастическое встраивание соседей (t-SNE).

Анализ главных компонентов (PCA): 

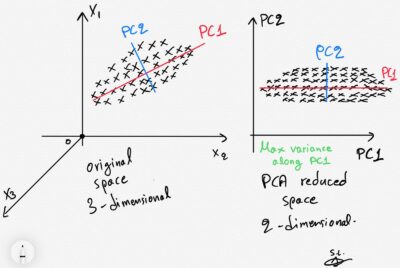
PCA, или анализ главных компонентов, является широко используемым методом уменьшения размерности. Основная идея PCA заключается в выявлении закономерностей во взаимоотношениях между переменными и представлении этих закономерностей в терминах меньшего числа переменных, называемых главными компонентами. Процедура PCA обычно включает в себя следующие этапы:

1. Стандартизация . Если входные переменные имеют разные масштабы, их обычно стандартизируют, чтобы они имели нулевое среднее значение и единичную дисперсию. Этот шаг гарантирует, что каждая переменная вносит равный вклад в анализ.
2. Расчет ковариационной матрицы . Следующим шагом является вычисление ковариационной матрицы стандартизированных данных. Ковариационная матрица описывает отношения между парами переменных и предоставляет информацию об их совместной изменчивости.
3. Разложение по собственным значениям : затем ковариационная матрица разлагается на собственные векторы и собственные значения. Собственные векторы представляют направления или основные компоненты данных, а собственные значения указывают величину дисперсии, объясняемую каждым главным компонентом. Собственные векторы сортируются в порядке убывания на основе соответствующих им собственных значений.
4. Выбор основных компонентов . Следующий шаг включает выбор подмножества основных компонентов для сохранения. Это решение может быть основано на кумулятивной объясненной дисперсии, где собственные значения нормализуются и суммируются. Обычный подход заключается в выборе топ-k главных компонентов, которые объясняют значительную часть общей дисперсии (например, 95% или 99%).
5. Проекция : выбранные основные компоненты используются для создания нового подпространства объектов. Исходные данные проецируются на это подпространство для получения преобразованного набора данных с уменьшенной размерностью. Эта проекция осуществляется путем умножения стандартизированных данных на матрицу выбранных собственных векторов.

t-распределенное стохастическое вложение соседей (t-SNE):  

Основная идея t-SNE состоит в том, чтобы преобразовать сходства между точками данных в многомерном пространстве в вероятности, а затем сопоставить эти вероятности с пространством более низкой размерности таким образом, чтобы максимально сохранить связи между точками данных. Процедура t-SNE включает следующие этапы:

1. Вычисление попарных сходств . Сначала вычисляются попарные сходства между точками данных в многомерном пространстве. Эти сходства обычно рассчитываются с использованием ядра Гаусса, которое измеряет сходство на основе евклидова расстояния между точками данных.
2. Построение распределений вероятностей . На основе попарных сходств строятся распределения вероятностей для каждой точки данных. Распределения представляют собой сходство между точкой данных и всеми другими точками в многомерном пространстве. Сходства преобразуются в вероятности с помощью функции softmax.
3. Инициализировать внедрение : Начальное внедрение точек данных в низкомерное пространство генерируется случайным образом. Каждой точке данных присваивается положение в низкоразмерном пространстве.
4. Вычисление сходства в низкомерном пространстве . Как и в многомерном пространстве, попарное сходство между точками данных вычисляется в низкомерном пространстве. Однако в низкомерном пространстве для моделирования парных сходств используется другое распределение, называемое t-распределением Стьюдента.
5. Оптимизация встраивания . Целью t-SNE является минимизация расхождения между попарными сходствами в многомерном пространстве и попарными сходствами в низкомерном пространстве. Это достигается посредством итеративного процесса оптимизации. Положения точек данных в низкомерном пространстве корректируются итеративно, чтобы минимизировать разницу между парными сходствами высокой и низкой размерности. Оптимизация обычно выполняется с использованием градиентного спуска.
6. Сходимость : процесс оптимизации продолжается до тех пор, пока не будет достигнут критерий остановки. Этим критерием может быть максимальное количество итераций, желаемый уровень сходимости или порог изменения позиций встраивания.
7. Визуализация : после завершения оптимизации можно визуализировать окончательное низкоразмерное встраивание. Точки данных отображаются в низкоразмерном пространстве, где их положение определяется оптимизированным встраиванием. Целью визуализации является представление сходств и взаимосвязей между точками данных таким образом, чтобы сохранить локальную и глобальную структуру многомерных данных.

Приближение и проекция равномерного многообразия (UMAP): 

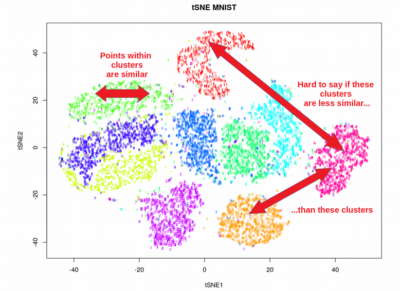
Основная идея UMAP заключается в построении низкомерного представления данных, сохраняющего глобальную и локальную структуру многомерного пространства. UMAP использует подход на основе графов для построения топологического представления данных, которое затем внедряется в низкоразмерное пространство с использованием стохастического градиентного спуска. Процедура UMAP включает в себя следующие этапы:

1. Вычисление попарных расстояний . Первым шагом является вычисление попарных расстояний между точками данных в многомерном пространстве. Выбор метрики расстояния зависит от характера данных и решаемой проблемы. Общие метрики расстояния включают евклидово расстояние, косинусное расстояние или корреляционное расстояние.
2. Постройте нечеткое симплициальное множество . На основе попарных расстояний строится нечеткое симплициальное множество. Нечеткий симплициальный набор представляет собой локальную структуру окрестностей точек данных. Он отражает понятие «близости» или «сходства» между точками данных, принимая во внимание плотность и связность данных.
3. Оптимизация низкоразмерного встраивания . Цель UMAP — найти низкоразмерное представление, сохраняющее отношения соседства, фиксируемые нечетким симплициальным набором. Это делается посредством процесса оптимизации. Первоначально генерируется случайное низкоразмерное вложение. Затем UMAP использует стохастический градиентный спуск, чтобы минимизировать несоответствие между попарными сходствами в многомерном и низкомерном пространстве.
4. Построение графа и выполнение его компоновки : UMAP создает представление графа на основе низкоразмерного встраивания. Этот график отражает глобальную структуру данных. Алгоритмы компоновки графика, такие как силовая компоновка или спектральная компоновка, применяются для позиционирования точек данных в низкоразмерном пространстве с учетом структуры графа.
5. Уточнить встраивание : UMAP выполняет этап уточнения для дальнейшего улучшения встраивания. Этот шаг включает в себя корректировку положения точек данных на основе структуры графика и связности данных.
6. Сходимость : этапы оптимизации и уточнения повторяются до тех пор, пока не будет достигнута сходимость. Сходимость может быть определена на основе заданного количества итераций или критерия остановки, например порога изменения позиций внедрения.
7. Визуализация и анализ . После завершения оптимизации окончательное низкоразмерное встраивание можно визуализировать и проанализировать. Низкоразмерное представление направлено на сохранение отношений соседства и глобальной структуры многомерных данных. Его можно использовать для визуализации, кластеризации или дальнейшего анализа.

Сравнение PCA, t-SNE и UMAP: 

1. Линейный и нелинейный : PCA — это метод уменьшения линейной размерности, который фокусируется на поиске ортогональных осей, которые объясняют максимальную дисперсию данных. Он эффективен для выявления глобальных закономерностей и уменьшения размерности данных. Напротив, t-SNE и UMAP — это нелинейные методы, целью которых является сохранение как локальных, так и глобальных структур данных, что делает их более подходящими для визуализации и исследования сложных взаимосвязей.
2. Сохранение глобальной и локальной структуры : PCA в первую очередь фокусируется на сохранении глобальной структуры данных, то есть его цель — уловить общую дисперсию и тенденции в наборе данных. Он может не сохранить мелкозернистую локальную структуру или шаблоны кластеризации в данных. С другой стороны, t-SNE и UMAP превосходно сохраняют локальную структуру, подчеркивая связи между близлежащими точками данных. Они могут выявить кластеры, закономерности и нелинейные отношения, которые могут быть скрыты в многомерном пространстве.
3. Время вычислений и масштабируемость : PCA эффективен в вычислительном отношении и может обрабатывать большие наборы данных. Это метод, основанный на линейной алгебре, который можно эффективно вычислять с помощью матричных операций. С другой стороны, t-SNE и UMAP требуют более интенсивных вычислений, особенно для больших наборов данных. Они включают в себя процедуры оптимизации и вычисления на основе графов, которые могут занять много времени. UMAP спроектирован так, чтобы быть более масштабируемым, чем t-SNE, и может более эффективно обрабатывать крупномасштабные наборы данных.
4. Интерпретируемость : PCA обеспечивает интерпретируемые результаты, поскольку основные компоненты представляют собой линейные комбинации исходных функций. Каждый главный компонент фиксирует определенную разницу в данных, и их вклад можно проанализировать. Напротив, t-SNE и UMAP создают преобразованные вложения в пространстве более низкой размерности, которые невозможно напрямую интерпретировать с точки зрения исходных функций. Они в основном используются для целей визуализации и исследования.
5. Пригодность для различных задач : PCA обычно используется для уменьшения размерности, выбора функций и снижения шума. Он также используется в качестве этапа предварительной обработки для различных алгоритмов машинного обучения. t-SNE и UMAP часто используются для визуализации и исследования данных. Они помогают выявить сложные структуры, кластеры и взаимосвязи в данных, что делает их ценными для таких задач, как исследовательский анализ данных, распознавание образов и обнаружение аномалий.
6. Настройка параметров : PCA не имеет большого количества настраиваемых параметров. Количество основных компонентов, которые необходимо сохранить, является ключевым решением, которое может быть основано на объяснении отклонений или знании предметной области. t-SNE и UMAP имеют больше параметров для настройки. Например, в t-SNE на результаты влияют сложность, скорость обучения и количество итераций. UMAP имеет такие параметры, как n_neighbours, min_dist и метрика, которые влияют на качество внедрения.

Встраиваемый проектор Tensorflow:

TensorFlow Embedding Projector — это веб-инструмент визуализации, предоставляемый TensorFlow, платформой машинного обучения с открытым исходным кодом, разработанной Google. Он разработан специально для визуализации многомерных внедрений, таких как векторные представления слов или изученные представления данных, в пространстве более низкой размерности.

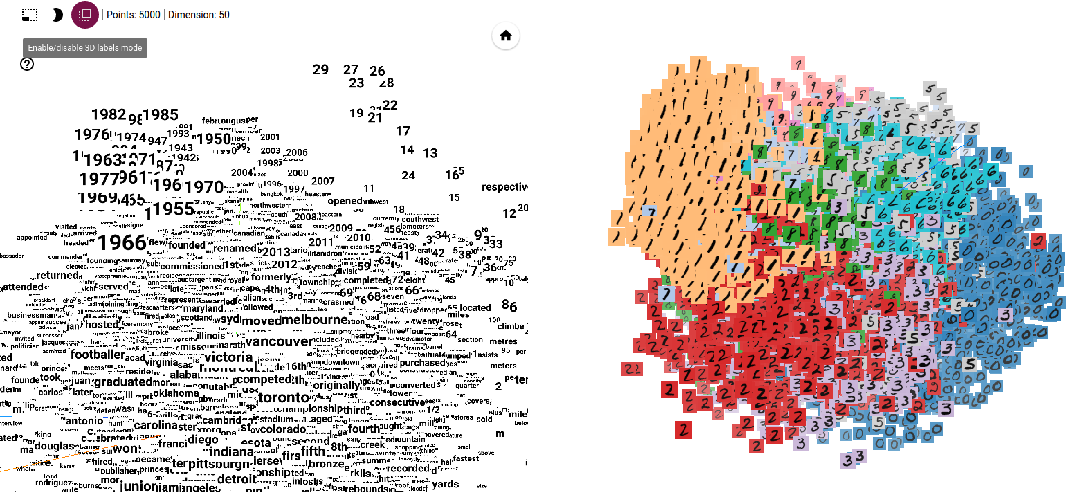
Проектор встраивания TensorFlow позволяет пользователям интерактивно исследовать и анализировать встраивания, предоставляя ценную информацию об отношениях, кластерах и закономерностях в данных. Он предлагает несколько функций и возможностей, в том числе:

1. 3D-диаграмма рассеяния : проектор для встраивания обеспечивает визуализацию 3D-диаграммы рассеяния, позволяя пользователям перемещаться и проверять встраивания под разными углами. Точки данных представлены в виде маркеров, и пользователи могут масштабировать, вращать и панорамировать график, чтобы исследовать пространственные отношения между внедрениями.
2. Метки и метаданные . Пользователи могут назначать метки точкам данных, предоставляя дополнительную информацию о каждом внедрении. Метки можно использовать для идентификации конкретных категорий, классов или объектов, связанных с данными. Кроме того, к каждой точке данных для дальнейшего анализа можно прикрепить метаданные, такие как дополнительные атрибуты или свойства вложений.
3. Раскраска и фильтрация . Встраиваемый проектор позволяет пользователям раскрашивать точки данных на основе определенных атрибутов или меток, что упрощает идентификацию кластеров или визуализацию закономерностей. Кроме того, пользователи могут применять фильтры, чтобы сосредоточиться на определенных подмножествах данных, выделяя определенные регионы или группы вложений.
4. Поиск по сходству : Embedding Projector включает функцию поиска по сходству, которая позволяет пользователям находить ближайших соседей выбранной точки данных на основе показателей сходства. Эта функция помогает идентифицировать вложения со схожими характеристиками или отношениями, помогая в исследовании и анализе данных.
5. Импорт и экспорт : Embedding Projector поддерживает импорт и экспорт вложений в различных форматах, включая контрольные точки TensorFlow, форматы word2vec и файлы TSV (значения, разделенные табуляцией). Эта гибкость позволяет пользователям работать с внедрениями, созданными из разных моделей или источников.

Источник: aurigait.com

Комментарии: