Иерархическая кластеризация
МЕНЮ
Главная страница
Поиск
Регистрация на сайте
Помощь проекту
Архив новостей
ТЕМЫ
Новости ИИ
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Искусственный интеллект
Слежка за людьми
Угроза ИИ
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Нейронные сети начинающим
Психология ИИ
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Творчество ИИ
Техническое зрение
Чат-боты
Авторизация
2024-07-07 11:06

Что такое иерархическая кластеризация?
Иерархическая кластеризация — популярный метод группировки объектов. Он создает группы так, чтобы объекты внутри группы были похожи друг на друга и отличались от объектов в других группах. Кластеры визуально представлены в виде иерархического дерева, называемого дендрограммой .
Иерархическая кластеризация имеет несколько ключевых преимуществ:
- Нет необходимости заранее указывать количество кластеров. Вместо этого дендрограмму можно разрезать на соответствующем уровне, чтобы получить желаемое количество кластеров.
- Данные легко суммируются/организуются в иерархию с помощью дендрограмм. Дендрограммы упрощают изучение и интерпретацию кластеров.
Приложения
Существует множество реальных применений иерархической кластеризации. Они включают:
- Биоинформатика: группировка животных по их биологическим особенностям для реконструкции филогенетических деревьев.
- Бизнес: разделение клиентов на сегменты или формирование иерархии сотрудников по зарплате.
- Обработка изображений: группировка рукописных символов при распознавании текста на основе сходства форм символов.
- Поиск информации: категоризация результатов поиска на основе запроса.
Типы иерархической кластеризации
Существует два основных типа иерархической кластеризации:
- Агломеративный : изначально каждый объект считается отдельным кластером. В соответствии с определенной процедурой кластеры затем объединяются шаг за шагом, пока не останется один кластер. В конце процесса объединения кластеров будет сформирован кластер, содержащий все элементы.
- Разделительный : метод разделения является противоположностью агломеративного метода. Изначально все объекты рассматриваются в одном кластере. Затем процесс разделения выполняется шаг за шагом, пока каждый объект не образует отдельный кластер. Процедура деления или расщепления кластера осуществляется по некоторым принципам, обеспечивающим максимальное расстояние между соседними объектами в кластере.
Между агломеративной и разделительной кластеризацией агломеративная кластеризация обычно является предпочтительным методом. В приведенном ниже примере основное внимание будет уделено алгоритмам агломеративной кластеризации, поскольку они являются наиболее популярными и простыми в реализации.
Этапы иерархической кластеризации
Иерархическая кластеризация использует меру расстояния/сходства для создания новых кластеров. Шаги агломеративной кластеризации можно резюмировать следующим образом:
- Шаг 1. Вычислите матрицу близости, используя конкретную метрику расстояния.
- Шаг 2. Каждая точка данных назначается кластеру.
- Шаг 3. Объедините кластеры на основе показателя сходства между кластерами.
- Шаг 4. Обновите матрицу расстояний.
- Шаг 5. Повторяйте шаги 3 и 4, пока не останется только один кластер.
Вычисление матрицы близости
Первым шагом алгоритма является создание матрицы расстояний. Значения матрицы вычисляются путем применения функции расстояния между каждой парой объектов. Для этой операции обычно используется функция евклидова расстояния . Структура матрицы близости будет следующей для набора данных с
элементы. Здесь,представляют значения расстояния междуи
.
Сходство между кластерами
Основной вопрос в иерархической кластеризации — как вычислить расстояние между кластерами и обновить матрицу близости. Для ответа на этот вопрос используется много разных подходов. Каждый подход имеет свои преимущества и недостатки. Выбор будет зависеть от того, есть ли в наборе данных шум, является ли форма кластеров круглой или нет, а также от плотности точек данных.
Численный пример поможет проиллюстрировать методы и варианты выбора. Мы будем использовать небольшой образец набора данных, содержащий всего девять двумерных точек, показанных на рисунке 1.
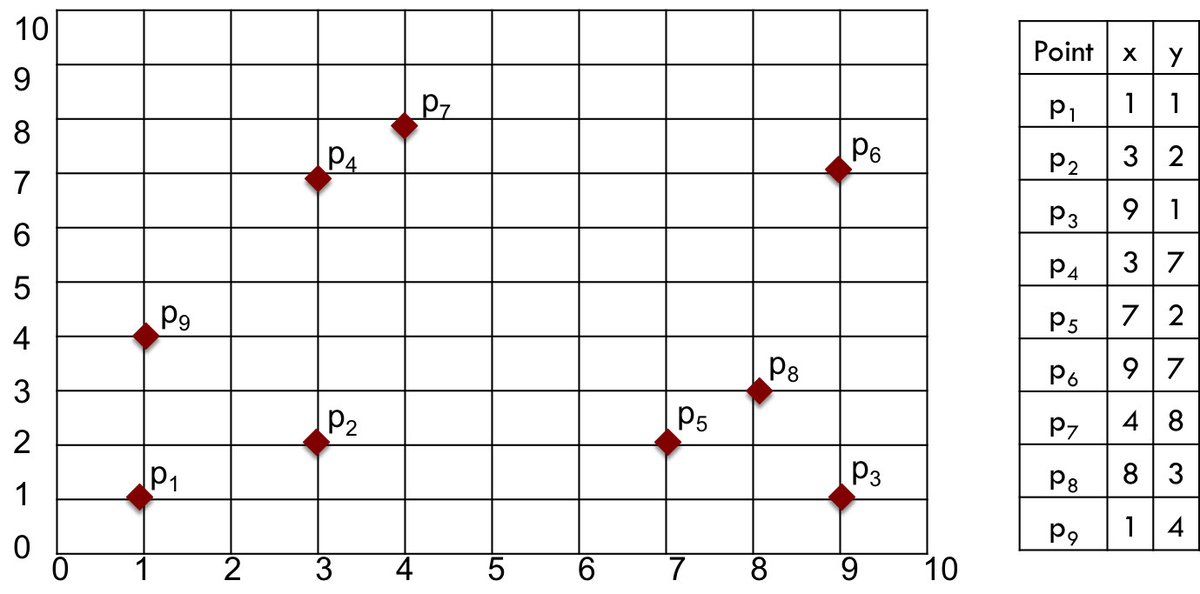
Рисунок 1: Пример данных

Предположим, у нас есть два кластера в образце набора данных, как показано на рисунке 2. Существуют разные подходы к вычислению расстояния между кластерами. Популярные методы перечислены ниже.

Рисунок 2: Два кластера

Минимальное (одиночное) соединение
Один из способов измерения расстояния между кластерами — найти минимальное расстояние между точками в этих кластерах. То есть мы можем найти точку в первом кластере, ближайшую к точке другого кластера, и вычислить расстояние между этими точками. На рисунке 2 ближайшие точки:
в одном кластере ив другом. Расстояние между этими точками и, следовательно, расстояние между кластерами находится как.
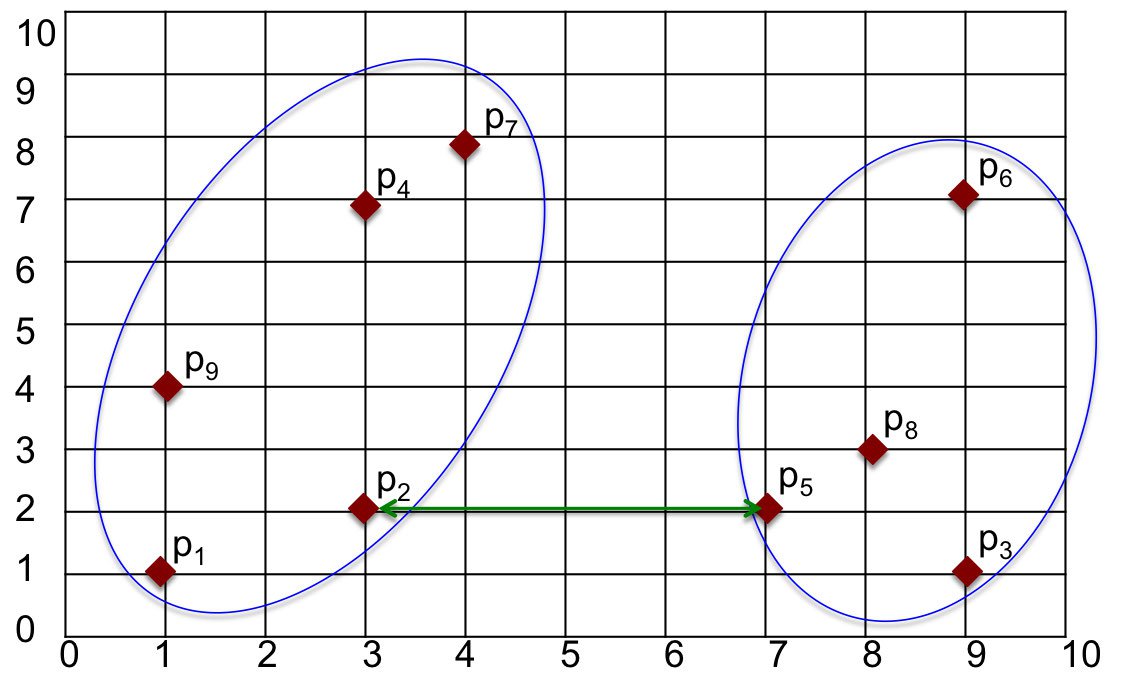
Рисунок 3: Метод минимальной связи

Преимущество метода Min в том, что он позволяет точно обрабатывать неэллиптические формы. Недостатком является то, что он чувствителен к шуму и выбросам.
Макс (Полное) Соединение
Другой способ измерения расстояния — найти максимальное расстояние между точками в двух кластерах. Мы можем найти точки в каждом кластере, которые находятся дальше всего друг от друга, и вычислить расстояние между этими точками. На рисунке 3 максимальное расстояние находится между
и. Расстояние между этими двумя точками и, следовательно, расстояние между кластерами находится как.

Рисунок 4: Метод максимальной связи

Макс менее чувствителен к шуму и выбросам по сравнению с методом MIN. Однако MAX может разрушать большие скопления и имеет тенденцию смещаться в сторону шаровых скоплений.
Центроидная связь
Метод Centroid определяет расстояние между кластерами как расстояние между их центрами/центроидами. После вычисления центроида для каждого кластера расстояние между этими центроидами вычисляется с помощью функции расстояния.
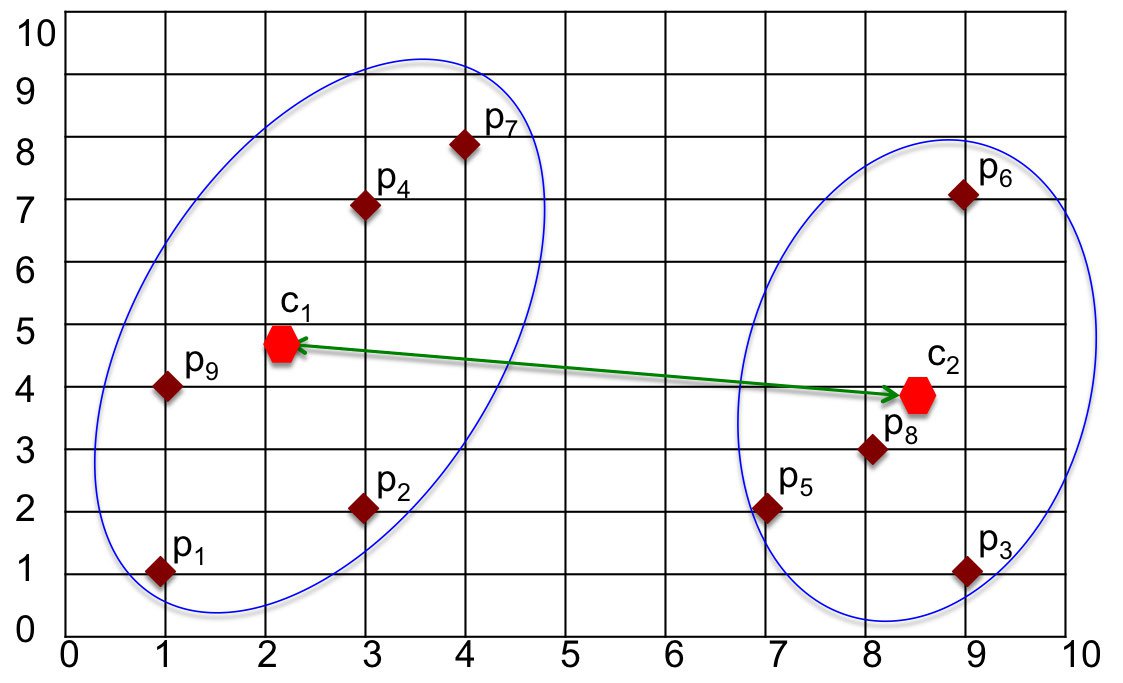
Рисунок 5. Метод центроидной связи.

Средняя связь
Метод Average определяет расстояние между кластерами как среднее попарное расстояние среди всех пар точек в кластерах. Для простоты на рисунке 6 показаны только некоторые линии, соединяющие пары точек.

Рисунок 6: Метод средней связи

Связь Уорда
Подход Уорда анализирует дисперсию кластеров, а не напрямую измеряет расстояния, минимизируя дисперсию между кластерами.
При использовании метода Уорда расстояние между двумя кластерами связано с тем, насколько увеличится значение суммы квадратов (SS) при объединении.
Другими словами, метод Уорда пытается минимизировать сумму квадратов расстояний точек от центров кластеров. По сравнению с описанными выше измерениями на основе расстояния метод Уорда менее восприимчив к шуму и выбросам. Поэтому метод Уорда предпочтительнее других при кластеризации.
Иерархическая кластеризация с Python
В Python библиотеки Scipyи Scikit-Learnопределили функции для иерархической кластеризации. В приведенных ниже примерах эти библиотечные функции используются для иллюстрации иерархической кластеризации в Python.
Сначала мы импортируем NumPy , matplotlib и seaborn (для стилизации графика):
import numpy as np import matplotlib.pyplot as plt import seaborn as sns sns.set_style('dark') Далее мы определим небольшой образец набора данных:
X1 = np.array([[1,1], [3,2], [9,1], [3,7], [7,2], [9,7], [4,8], [8,3],[1,4]]) Давайте изобразим этот набор данных в виде точечной диаграммы:
plt.figure(figsize=(6, 6)) plt.scatter(X1[:,0], X1[:,1], c='r') # Create numbered labels for each point for i in range(X1.shape[0]): plt.annotate(str(i), xy=(X1[i,0], X1[i,1]), xytext=(3, 3), textcoords='offset points') plt.xlabel('x coordinate') plt.ylabel('y coordinate') plt.title('Scatter Plot of the data') plt.xlim([0,10]), plt.ylim([0,10]) plt.xticks(range(10)), plt.yticks(range(10)) plt.grid() plt.show() РЕЗУЛЬТАТ:
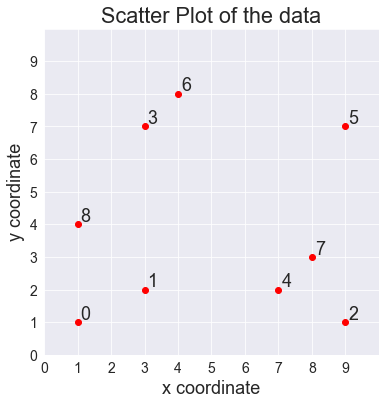
Теперь мы будем использовать этот набор данных для выполнения иерархической кластеризации.
Иерархическая кластеризация с использованием Scipy
В библиотеке Scipy имеется linkageфункция иерархической (агломеративной) кластеризации.
Функция linkageимеет несколько методов расчета расстояния между кластерами: одиночный, средний, взвешенный, центроидный, медианный и вардный . Ниже мы сравним эти методы. Подробнее о linkageфункции смотрите в документации .
Чтобы нарисовать дендрограмму, мы воспользуемся функцией dendrogram. Опять же, подробнее о dendrogramфункции смотрите в документации .
Сначала мы импортируем необходимые функции, а затем сможем формировать связи с помощью различных методов:
from scipy.cluster.hierarchy import dendrogram, linkage Z1 = linkage(X1, method='single', metric='euclidean') Z2 = linkage(X1, method='complete', metric='euclidean') Z3 = linkage(X1, method='average', metric='euclidean') Z4 = linkage(X1, method='ward', metric='euclidean') Теперь, передав dendrogramфункцию в matplotlib, мы можем просмотреть график этих связей:
plt.figure(figsize=(15, 10)) plt.subplot(2,2,1), dendrogram(Z1), plt.title('Single') plt.subplot(2,2,2), dendrogram(Z2), plt.title('Complete') plt.subplot(2,2,3), dendrogram(Z3), plt.title('Average') plt.subplot(2,2,4), dendrogram(Z4), plt.title('Ward') plt.show() РЕЗУЛЬТАТ:
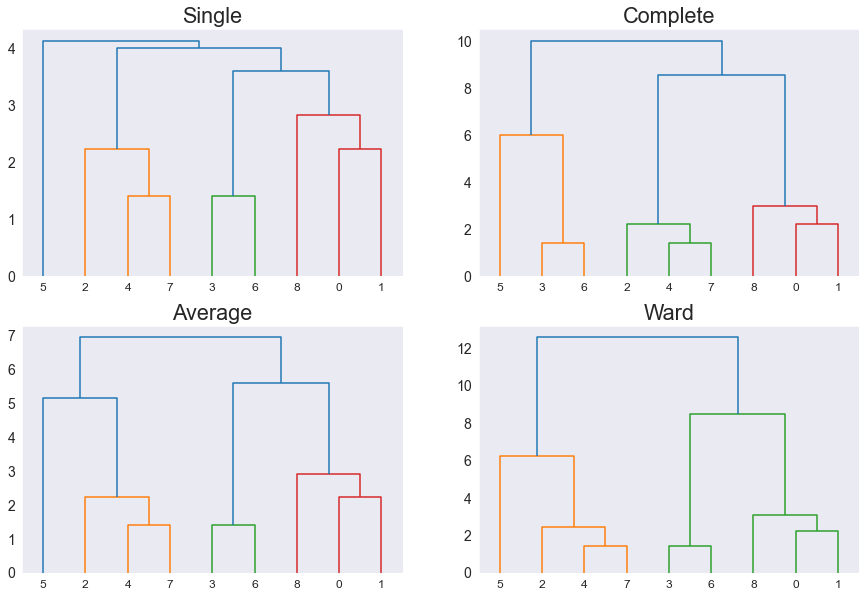
Обратите внимание, что каждый метод расстояния создает разные связи для одних и тех же данных.
Наконец, давайте воспользуемся функцией fcluster, чтобы найти кластеры для связи Уорда:
from scipy.cluster.hierarchy import fcluster f1 = fcluster(Z4, 2, criterion='maxclust') print(f"Clusters: {f1}") Вне:
Clusters: [2 2 1 2 1 1 2 1 2] Функция fclusterдает метки кластеров в том же индексе, что и набор данных X1. Например, индекс один из f1is 2, который является кластером для записи с индексом один из X1, который равен [1, 1].
Вне:
X1 Cluster [1 1] --> 2 [3 2] --> 2 [9 1] --> 1 [3 7] --> 2 [7 2] --> 1 [9 7] --> 1 [4 8] --> 2 [8 3] --> 1 [1 4] --> 2 Иерархическая кластеризация с использованием Scikit-Learn
В библиотеке Scikit-Learn есть собственная функция агломеративной иерархической кластеризации: AgglomerativeClustering.
Варианты расчета расстояния между кластерами включают палатный, полный, средний и одиночный . Для получения более конкретной информации вы можете найти этот класс в соответствующей документации.
Использование sklearn немного отличается от scipy. Нам нужно импортировать AgglomerativveClusteringкласс, а затем создать его экземпляр, указав количество желаемых кластеров и linkageфункцию расстояния ( ), которую мы будем использовать. Затем мы используем fit_predictдля обучения и прогнозирования кластеров, используя X1набор данных:
from sklearn.cluster import AgglomerativeClustering Z1 = AgglomerativeClustering(n_clusters=2, linkage='ward') Z1.fit_predict(X1) print(Z1.labels_) Вне:
[0 0 1 0 1 1 0 1 0] Опять же, вот совпадение для каждой записи X1и соответствующего кластера:
Вне:
X1 Cluster [1 1] --> 0 [3 2] --> 0 [9 1] --> 1 [3 7] --> 0 [7 2] --> 1 [9 7] --> 1 [4 8] --> 0 [8 3] --> 1 [1 4] --> 0 Следующий код рисует диаграмму рассеяния, используя метки кластера.
fig, ax = plt.subplots(figsize=(6, 6)) scatter = ax.scatter(X1[:,0], X1[:,1], c=Z1.labels_, cmap='rainbow') legend = ax.legend(*scatter.legend_elements(), title="Clusters", bbox_to_anchor=(1, 1)) ax.add_artist(legend) plt.title('Scatter plot of clusters') plt.show() РЕЗУЛЬТАТ:

Обратите внимание, что цвет каждой точки указывает на то, как данные были сгруппированы в левую и правую области.
Кластеризация реального набора данных
В предыдущем разделе иерархическая кластеризация выполнялась на простом наборе данных. В следующем разделе иерархическая кластеризация будет выполняться на реальных данных для решения реальной проблемы.
Здесь мы используем набор данных из книги «Биостатистика с R» , который содержит информацию о девяти различных источниках белка и их соответствующем потреблении в разных странах. Мы будем использовать эти данные, чтобы сгруппировать страны в соответствии с их потреблением белка.
Сначала мы прочитаем CSV и отобразим первые несколько строк данных:
import pandas as pd df = pd.read_csv('https://raw.githubusercontent.com/LearnDataSci/glossary/main/data/protein.csv') df.head() Вне:
| Страна | Красное мясо | Белое мясо | Яйца | Молоко | Рыба | Хлопья | Крахмал | Орехи | О.Вег | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Албания | 10.1 | 1,4 | 0,5 | 8,9 | 0,2 | 42,3 | 0,6 | 5,5 | 1,7 |
| 1 | Австрия | 8,9 | 14,0 | 4.3 | 19,9 | 2.1 | 28,0 | 3.6 | 1.3 | 4.3 |
| 2 | Бельгия | 13,5 | 9.3 | 4.1 | 17,5 | 4,5 | 26,6 | 5,7 | 2.1 | 4.0 |
| 3 | Болгария | 7,8 | 6.0 | 1,6 | 8.3 | 1.2 | 56,7 | 1.1 | 3.7 | 4.2 |
| 4 | Чехословакия | 9,7 | 11.4 | 2,8 | 12,5 | 2.0 | 34,3 | 5.0 | 1.1 | 4.0 |
Сначала сохраним в файле функции для кластеризации X2, которые содержатся во всех строках и столбцах от 1 до 10:
X2 = df.iloc[:,1:10] Опять же, мы используем функцию связи для кластеризации данных:
Z2 = linkage(X2, method='ward', metric='euclidean') Наконец, мы можем построить дендрограмму кластеризации 25 стран, основанную на их потреблении белка:
labelList = list(df['Country']) plt.figure(figsize=(13, 12)) dendrogram( Z2, orientation='right', labels=labelList, distance_sort='descending', show_leaf_counts=False, leaf_font_size=16 ) plt.show() РЕЗУЛЬТАТ:
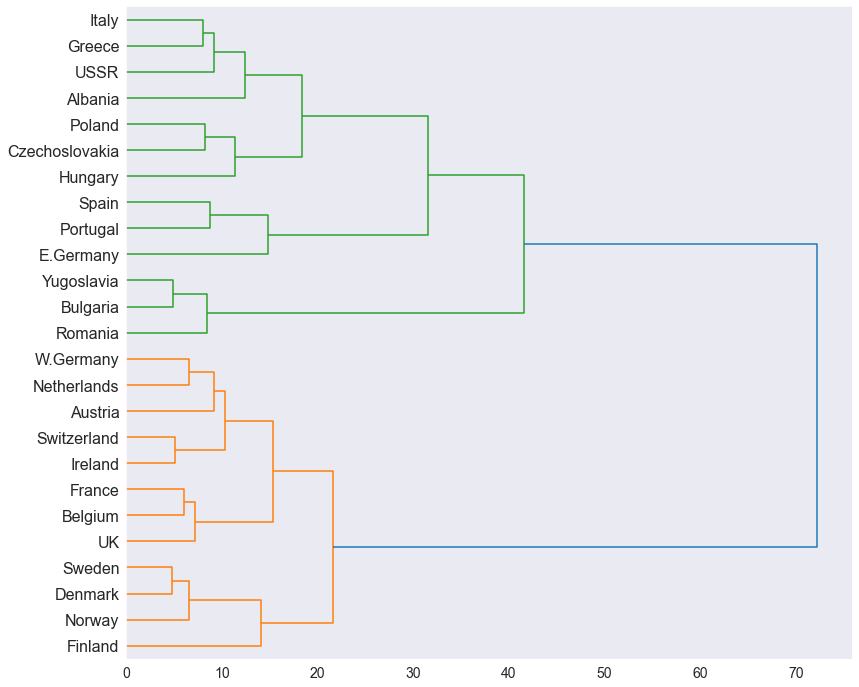
На дендрограмме мы можем наблюдать два отдельных кластера, окрашенных в зеленый и желтый цвета. Этот результат указывает на то, что страны в каждом кластере получают белок из аналогичных источников.
Используя эту fclusterфункцию, мы можем найти и добавить метки кластера для каждой страны в фрейм данных.
df['Clusters'] = fcluster(Z2, 2, criterion='maxclust') df.head() Вне:
| Страна | Красное мясо | Белое мясо | Яйца | Молоко | Рыба | Хлопья | Крахмал | Орехи | О.Вег | Кластеры | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | Албания | 10.1 | 1,4 | 0,5 | 8,9 | 0,2 | 42,3 | 0,6 | 5,5 | 1,7 | 2 |
| 1 | Австрия | 8,9 | 14,0 | 4.3 | 19,9 | 2.1 | 28,0 | 3.6 | 1.3 | 4.3 | 1 |
| 2 | Бельгия | 13,5 | 9.3 | 4.1 | 17,5 | 4,5 | 26,6 | 5,7 | 2.1 | 4.0 | 1 |
| 3 | Болгария | 7,8 | 6.0 | 1,6 | 8.3 | 1.2 | 56,7 | 1.1 | 3.7 | 4.2 | 2 |
| 4 | Чехословакия | 9,7 | 11.4 | 2,8 | 12,5 | 2.0 | 34,3 | 5.0 | 1.1 | 4.0 | 2 |
Отсюда мы можем использовать этот результат кластеризации для улучшения других анализов, которые мы выполняем над данными.
Источник: www.learndatasci.com