Начало работы с кластеризацией k-средних в Python

Представьте, что вы опытный маркетолог, организующий новую кампанию для продукта и хотите найти подходящие сегменты для таргетинга, или вы юрист, заинтересованный в группировке различных документов в зависимости от их содержания, или вы анализируете транзакции по кредитным картам, чтобы выявить схожие закономерности. Во всех этих и многих других случаях наука о данных может использоваться для кластеризации ваших данных. Кластерный анализ — важная область обучения без учителя, которая помогает нам группировать данные. В прошлом мы обсуждали в этом блоге разницу между обучением с учителем и без учителя.  Напоминаем, что мы используем обучение без учителя, когда помеченные данные недоступны для наших целей, но мы хотим изучить общие особенности данных. В приведенных выше примерах мы, как маркетологи, можем обнаружить общие демографические характеристики нашей целевой аудитории, или как юрист, мы устанавливаем различные общие темы в рассматриваемых документах, или, как аналитик по мошенничеству, мы устанавливаем общие транзакции, которые могут выделить отклонения в чьем-то аккаунте. .

Во всех этих случаях кластеризация помогает найти эти общие следы, и существует множество алгоритмов кластеризации. В предыдущем посте мы говорили о кластеризации на основе плотности и обсуждали ее использование для обнаружения аномалий, аналогично примеру использования транзакций по кредитным картам, описанному выше. В этом посте мы утверждали, что другие алгоритмы могут быть легче понять и реализовать, например, k-средние, и цель этого поста — сделать именно это.

Сначала мы установим понятие кластера и определим важную часть в реализации k-средних: центроиды. Мы увидим, как k-means подходит к проблеме сходства и как группы обновляются на каждой итерации, пока не будет выполнено условие остановки. Мы проиллюстрируем это реализацией Python и закончим рассмотрением того, как использовать этот алгоритм через библиотеку Scikit-learn .

Вы можете использовать код из этого поста на своем компьютере, если у вас установлен Python 3.x. Альтернативно вы можете просто подписаться на бесплатный пробный доступ к платформе Domino MLOps и напрямую получить доступ к коду, используемому в этой статье (используйте кнопку «Доступ к проекту» в конце статьи). Давайте начнем.

К-средство – что это значит?

Мы упомянули, что заинтересованы в обнаружении общих черт между нашими наблюдениями за данными. Один из способов определить эту общность или сходство — измерить расстояние между точками данных. Чем короче расстояние, тем более схожи наблюдения. Существуют разные способы измерения этого расстояния, и один из них, который очень знаком многим людям, — это евклидово расстояние. Это верно! Тому же, чему нас учат, изучая теорему Пифагора. Давайте посмотрим и рассмотрим два наблюдения над двумя атрибутами (a) и (b). Точка (p_1) имеет координаты ((a_1,b_1 )) и точка (p_2=(a_2,b_2 )).

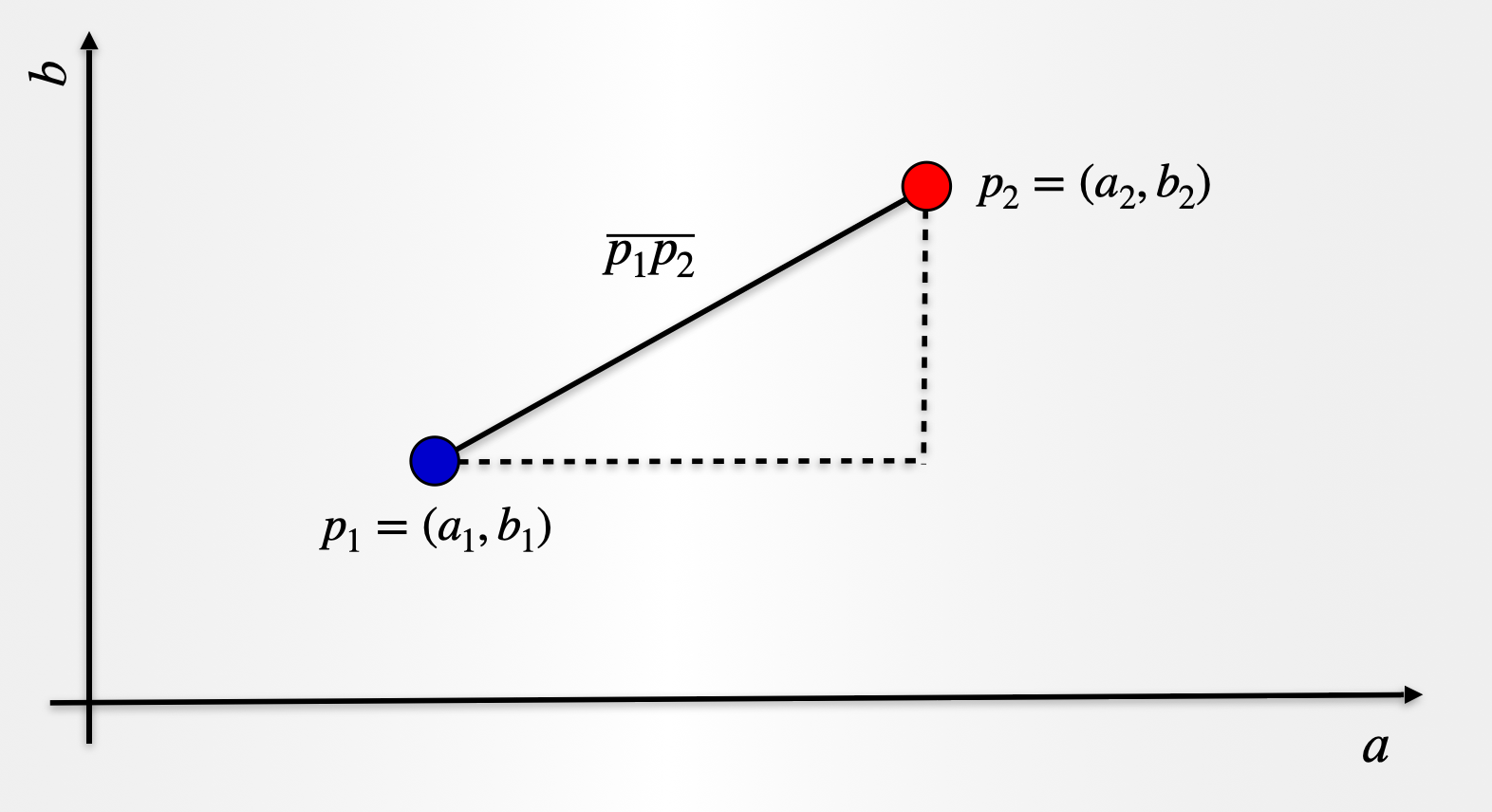
Расстояние (overline{p_1 p_2 }) определяется по формуле:

$$overline{p_1 p_2 }=sqrt{(a_2-a_1 )^2+(b_2-b_1 )^2 }$$

Выражение выше можно расширить до более чем двух атрибутов, и расстояние можно измерить между любыми двумя точками. Для набора данных с наблюдениями (n) мы предполагаем, что существуют группы или кластеры (k), и наша цель — определить, какое наблюдение соответствует любой из этих групп (k). Это важный момент, на который следует обратить внимание: алгоритм не даст нам количество кластеров, вместо этого нам нужно заранее определить число(k). Возможно, нам удастся запустить алгоритм с разными значениями (k) и определить наилучшее возможное решение.

Короче говоря, кластеризация (k)-средних пытается минимизировать расстояния между наблюдениями, принадлежащими кластеру, и максимизировать расстояние между различными кластерами. Таким образом, мы имеем связь между наблюдениями, принадлежащими одной группе, в то время как наблюдения, принадлежащие другой группе, остаются дальше друг от друга. Обратите внимание, что, как мы объяснили в этом посте , (k)-средние являются исчерпывающими в том смысле, что каждое отдельное наблюдение в наборе данных будет вынуждено быть частью одного из предполагаемых (k) кластеров.

Теперь должно быть ясно, откуда берется (k) в (k)-means, но как насчет части «средства»? Что ж, оказывается, что в рамках алгоритма мы также хотим определить центр каждого кластера. Мы называем это центроидом , и по мере того, как мы присваиваем наблюдения тому или иному кластеру, мы обновляем положение центроида кластера . Это делается путем взятия среднего значения (если хотите, среднего) всех точек данных, включенных в этот кластер. Легкий!

Рецепт k-средств

Рецепт (k)-средних довольно прост.

1. Решите, сколько кластеров вы хотите, т. е. выберите k
2. Случайным образом назначьте центроид каждому из k кластеров
3. Рассчитайте расстояние всех наблюдений до каждого из k центроидов.
4. Назначьте наблюдения ближайшему центроиду
5. Найдите новое местоположение центроида, взяв среднее значение всех наблюдений в каждом кластере.
6. Повторяйте шаги 3–5, пока центроиды не изменят положение.

И вуаля!

Взгляните на изображение ниже, где шаги схематически изображены для двумерного пространства. Те же шаги можно применить к большему количеству измерений (т. е. к большему количеству функций или атрибутов). Для простоты на схеме мы показываем только расстояние, измеренное до ближайшего центроида, но на практике необходимо учитывать все расстояния.

Начиная

Для целей нашей реализации мы для простоты рассмотрим некоторые данные с двумя атрибутами. Затем мы рассмотрим пример с большей размерностью. Для начала мы будем использовать подготовленный нами набор данных, который доступен здесь под именем kmeans_blobs.csv. Набор данных содержит 4 столбца со следующей информацией:

1. ID : уникальный идентификатор наблюдения.
2. x : Атрибут, соответствующий координате x.
3. y : Атрибут, соответствующий любой координате
4. Кластер : идентификатор кластера, к которому принадлежит наблюдение.

Мы отбросим столбец 4 для нашего анализа, но он может быть полезен для проверки результатов применения (k)-средних. Позже мы сделаем это во втором примере. Начнем с чтения набора данных:

import numpy as np import pandas as pd  import matplotlib.pyplot as plt from matplotlib.colors import ListedColormap %matplotlib inline  blobs = pd.read_csv('kmeans_blobs.csv') colnames = list(blobs.columns[1:-1]) blobs.head()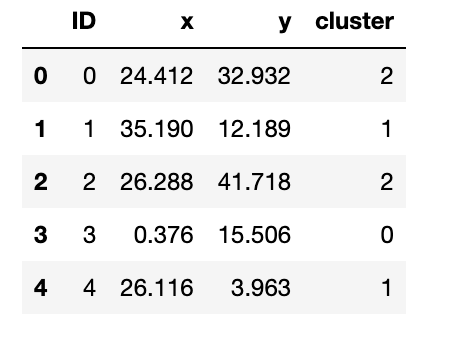 

Давайте посмотрим на наблюдения в наборе данных. Мы будем использовать столбец «Кластер», чтобы показать различные группы, присутствующие в наборе данных. Наша цель — увидеть, точно ли применение алгоритма воспроизводит группировки.

customcmap = ListedColormap(["crimson", "mediumblue", "darkmagenta"])  fig, ax = plt.subplots(figsize=(8, 6)) plt.scatter(x=blobs['x'], y=blobs['y'], s=150,             c=blobs['cluster'].astype('category'),              cmap = customcmap) ax.set_xlabel(r'x', fontsize=14) ax.set_ylabel(r'y', fontsize=14) plt.xticks(fontsize=12) plt.yticks(fontsize=12) plt.show()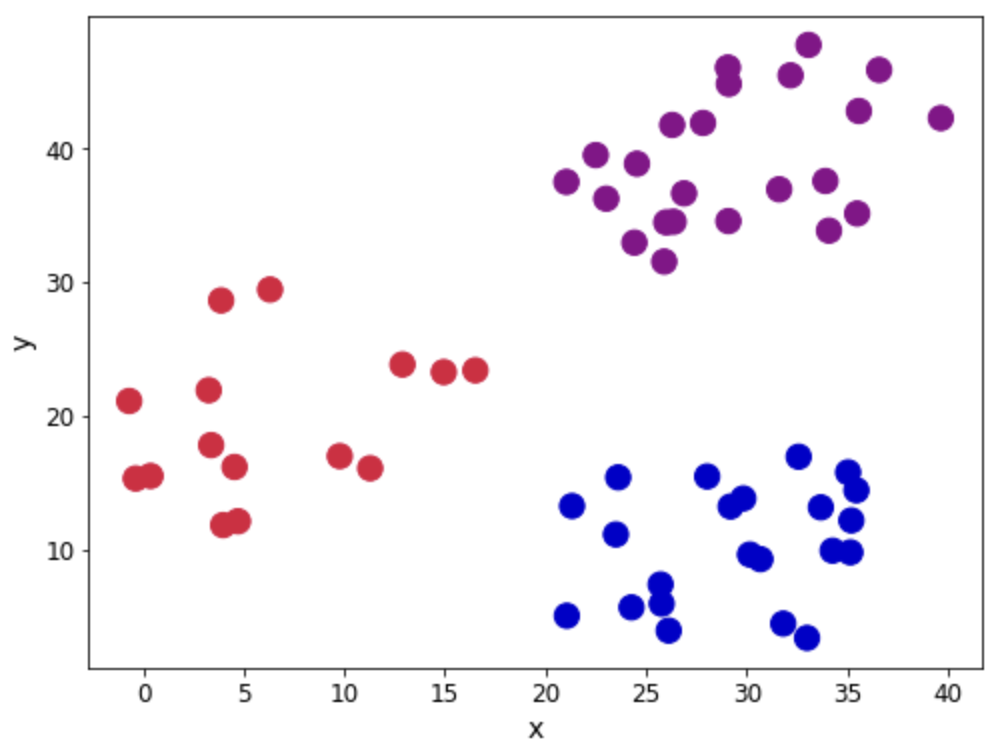

Давайте теперь посмотрим на наш рецепт.

Шаги 1 и 2. Определите (k) и инициируйте центроиды.

Сначала нам нужно 1) решить, сколько у нас групп, и 2) случайным образом назначить начальные центроиды. В этом случае давайте рассмотрим (k=3), а что касается центроидов, то они должны находиться в том же диапазоне, что и сам набор данных. Таким образом, один из вариантов — случайным образом выбрать наблюдения (k) и использовать их координаты для инициализации центроидов:

def initiate_centroids(k, dset):     '''     Select k data points as centroids     k: number of centroids     dset: pandas dataframe     '''     centroids = dset.sample(k)     return centroids  np.random.seed(42) k=3 df = blobs[['x','y']] centroids = initiate_centroids(k, df) centroids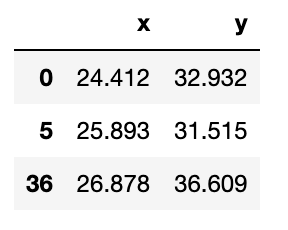

Шаг 3 – Рассчитайте расстояние

Теперь нам нужно вычислить расстояние между каждым из центроидов и точками данных. Мы назначим точку данных центроиду, который даст нам минимальную ошибку. Создадим функцию для вычисления корня квадратной ошибки:

def rsserr(a,b):     '''     Calculate the root of sum of squared errors.      a and b are numpy arrays     '''     return np.square(np.sum((a-b)**2)) 

Давайте выберем точку данных и вычислим ошибку, чтобы увидеть, как это работает на практике. Мы будем использовать точку, которая на самом деле является одним из центроидов, которые мы выбрали выше. Таким образом, мы ожидаем, что ошибка для этой точки и третьего центроида равна нулю. Поэтому мы бы присвоили эту точку данных второму центроиду. Давайте взглянем:

for i, centroid in enumerate(range(centroids.shape[0])):     err = rsserr(centroids.iloc[centroid,:], df.iloc[36,:])     print('Error for centroid {0}: {1:.2f}'.format(i, err))

Error for centroid 0: 384.22 Error for centroid 1: 724.64 Error for centroid 2: 0.00

Шаг 4. Назначьте центроиды

Мы можем использовать идею шага 3 для создания функции, которая поможет нам назначить точки данных соответствующим центроидам. Мы вычислим все ошибки, связанные с каждым центроидом, а затем выберем для присвоения тот, у которого наименьшее значение:

def centroid_assignation(dset, centroids):     '''     Given a dataframe `dset` and a set of `centroids`, we assign each     data point in `dset` to a centroid.      - dset - pandas dataframe with observations     - centroids - pa das dataframe with centroids     '''     k = centroids.shape[0]     n = dset.shape[0]     assignation = []     assign_errors = []      for obs in range(n):         # Estimate error         all_errors = np.array([])         for centroid in range(k):             err = rsserr(centroids.iloc[centroid, :], dset.iloc[obs,:])             all_errors = np.append(all_errors, err)          # Get the nearest centroid and the error         nearest_centroid =  np.where(all_errors==np.amin(all_errors))[0].tolist()[0]         nearest_centroid_error = np.amin(all_errors)          # Add values to corresponding lists         assignation.append(nearest_centroid)         assign_errors.append(nearest_centroid_error)      return assignation, assign_errors

Давайте добавим к нашим данным несколько столбцов, содержащих назначения центроидов и возникшую ошибку. Кроме того, мы можем использовать это для обновления нашей диаграммы рассеяния, показывающей центроиды (обозначенные квадратами), и раскрашиваем наблюдения в соответствии с центроидом, которому они были назначены:

df['centroid'], df['error'] = centroid_assignation(df, centroids) df.head()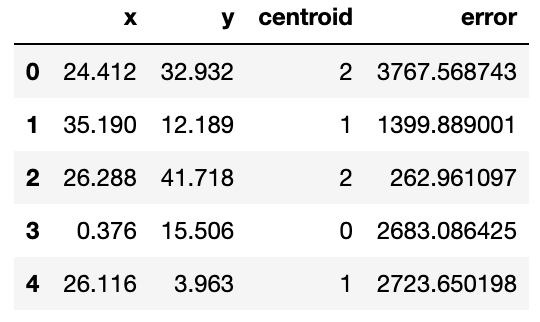

fig, ax = plt.subplots(figsize=(8, 6)) plt.scatter(df.iloc[:,0], df.iloc[:,1],  marker = 'o',              c=df['centroid'].astype('category'),              cmap = customcmap, s=80, alpha=0.5) plt.scatter(centroids.iloc[:,0], centroids.iloc[:,1],               marker = 's', s=200, c=[0, 1, 2],              cmap = customcmap) ax.set_xlabel(r'x', fontsize=14) ax.set_ylabel(r'y', fontsize=14) plt.xticks(fontsize=12) plt.yticks(fontsize=12) plt.show()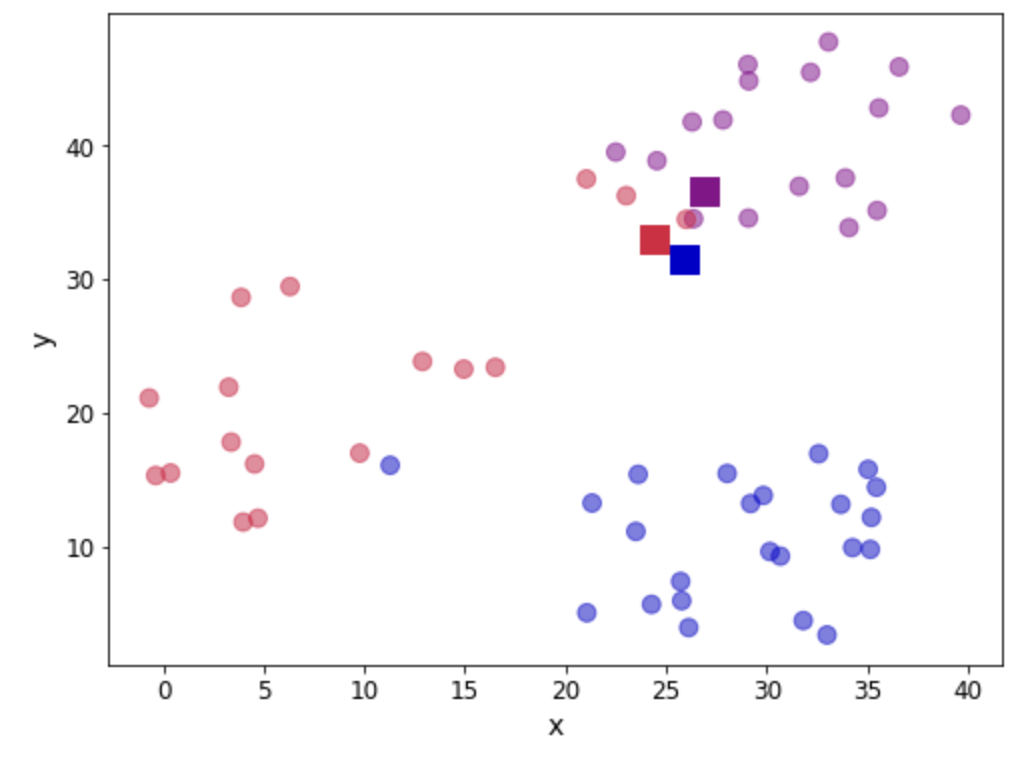

Давайте посмотрим на общую ошибку, сложив все вклады. Мы рассмотрим эту ошибку как меру сходимости. Другими словами, если ошибка не изменится, мы можем считать, что центроиды стабилизировали свое положение, и мы можем прекратить наши итерации. На практике нам нужно помнить о том, что мы нашли локальный минимум (выходящий за рамки этой статьи).

print("The total error is {0:.2f}".format(df['error'].sum()))

The total error is 11927659.01

Шаг 5. Обновите местоположение центроида.

Теперь, когда у нас есть первая попытка определить наши кластеры, нам нужно обновить положение k центроидов. Мы делаем это, вычисляя среднее значение положения наблюдений, присвоенных каждому центроиду. Давайте посмотрим:

centroids = df.groupby('centroid').agg('mean').loc[:, colnames].reset_index(drop = True) centroids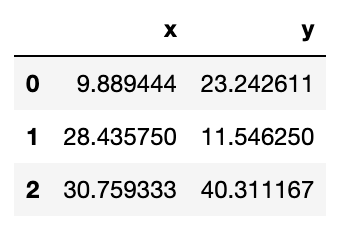

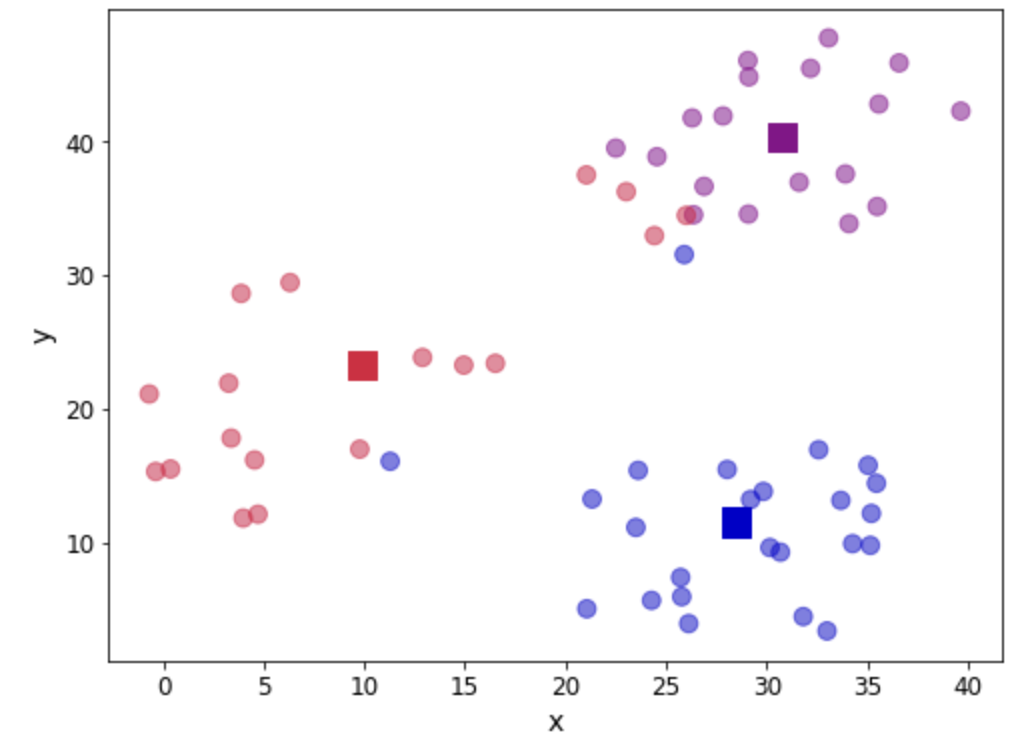
Мы можем убедиться, что позиция была обновлена. Давайте еще раз посмотрим на нашу диаграмму рассеяния:

fig, ax = plt.subplots(figsize=(8, 6)) plt.scatter(df.iloc[:,0], df.iloc[:,1],  marker = 'o',              c=df['centroid'].astype('category'),              cmap = customcmap, s=80, alpha=0.5) plt.scatter(centroids.iloc[:,0], centroids.iloc[:,1],               marker = 's', s=200,             c=[0, 1, 2], cmap = customcmap) ax.set_xlabel(r'x', fontsize=14) ax.set_ylabel(r'y', fontsize=14) plt.xticks(fontsize=12) plt.yticks(fontsize=12) plt.show()

Шаг 6. Повторите шаги 3–5.

Теперь мы возвращаемся, чтобы вычислить расстояние до каждого центроида, назначить наблюдения и обновить местоположение центроида. Это вызывает функцию для инкапсуляции цикла:

def kmeans(dset, k=2, tol=1e-4):     '''     K-means implementationd for a      `dset`:  DataFrame with observations     `k`: number of clusters, default k=2     `tol`: tolerance=1E-4     '''     # Let us work in a copy, so we don't mess the original     working_dset = dset.copy()     # We define some variables to hold the error, the      # stopping signal and a counter for the iterations     err = []     goahead = True     j = 0          # Step 2: Initiate clusters by defining centroids      centroids = initiate_centroids(k, dset)      while(goahead):         # Step 3 and 4 - Assign centroids and calculate error         working_dset['centroid'], j_err = centroid_assignation(working_dset, centroids)          err.append(sum(j_err))                  # Step 5 - Update centroid position         centroids = working_dset.groupby('centroid').agg('mean').reset_index(drop = True)          # Step 6 - Restart the iteration         if j>0:             # Is the error less than a tolerance (1E-4)             if err[j-1]-err[j]<=tol:                 goahead = False         j+=1      working_dset['centroid'], j_err = centroid_assignation(working_dset, centroids)     centroids = working_dset.groupby('centroid').agg('mean').reset_index(drop = True)     return working_dset['centroid'], j_err, centroids

Хорошо, теперь мы готовы применить нашу функцию. Сначала мы очистим наш набор данных и дадим алгоритму поработать:

np.random.seed(42) df['centroid'], df['error'], centroids =  kmeans(df[['x','y']], 3) df.head()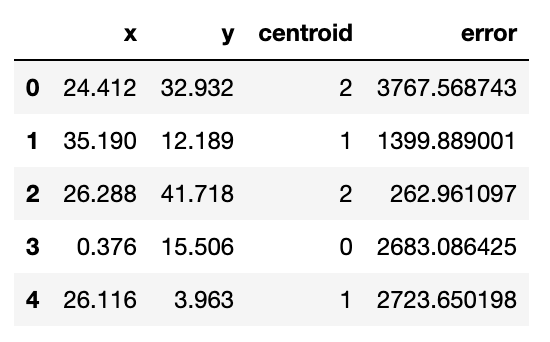

Давайте посмотрим расположение последних центроидов:

centroids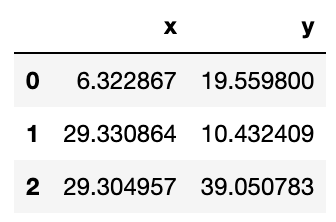

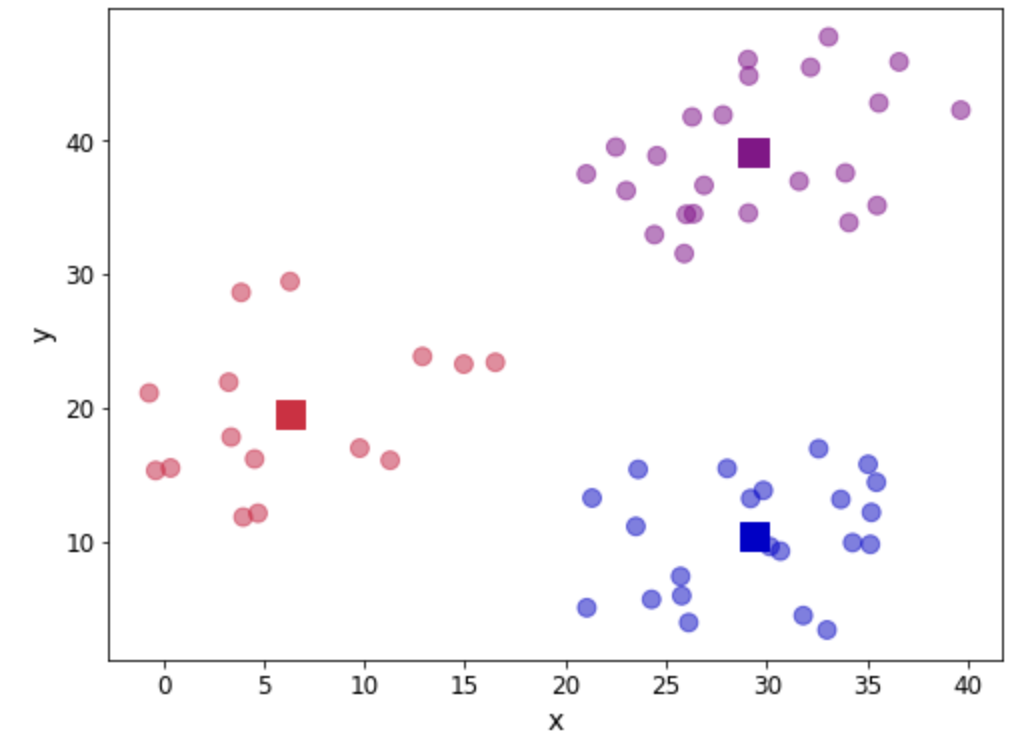
И графически посмотрим на наши кластеры:

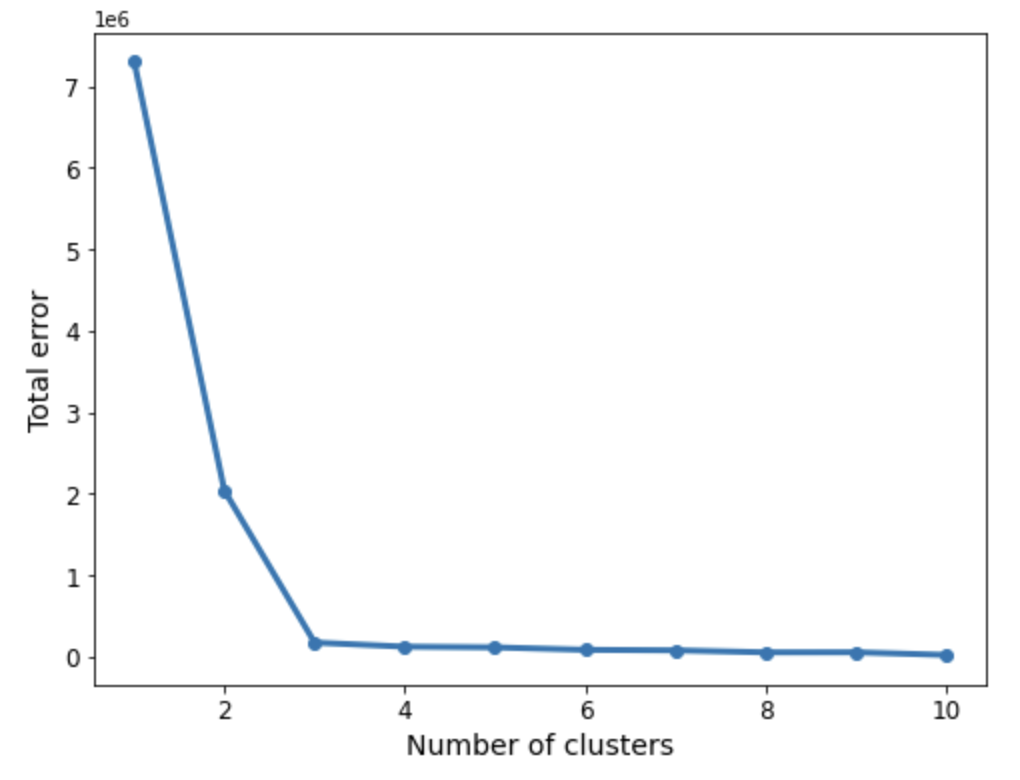
fig, ax = plt.subplots(figsize=(8, 6)) plt.scatter(df.iloc[:,0], df.iloc[:,1],  marker = 'o',              c=df['centroid'].astype('category'),              cmap = customcmap, s=80, alpha=0.5) plt.scatter(centroids.iloc[:,0], centroids.iloc[:,1],               marker = 's', s=200, c=[0, 1, 2],              cmap = customcmap) ax.set_xlabel(r'x', fontsize=14) ax.set_ylabel(r'y', fontsize=14) plt.xticks(fontsize=12) plt.yticks(fontsize=12) plt.show()

Как мы видим, получены три группы. В этом конкретном примере данные таковы, что различие между группами четкое. Однако не во всех случаях нам может повезти так же. Так что вопрос о том, сколько групп существует, все еще остается. Мы можем использовать экранный график, чтобы минимизировать ошибки, рассматривая запуск алгоритма с последовательностью (k=1,2,3,4,...) и ища «колено» на графике, обозначающее большое количество кластеров для использования:

err_total = [] n = 10  df_elbow = blobs[['x','y']]  for i in range(n):     _, my_errs, _ = kmeans(df_elbow, i+1)     err_total.append(sum(my_errs)) fig, ax = plt.subplots(figsize=(8, 6)) plt.plot(range(1,n+1), err_total, linewidth=3, marker='o') ax.set_xlabel(r'Number of clusters', fontsize=14) ax.set_ylabel(r'Total error', fontsize=14) plt.xticks(fontsize=12) plt.yticks(fontsize=12) plt.show()

Теперь мы можем применить «правило локтя», которое является эвристикой и помогает нам определить количество кластеров. Если мы думаем о линии, показанной выше, как об изображении руки, то «локоть» — это точка перегиба. В данном случае «колено» расположено между 2 и 4 кластерами, что указывает на то, что выбор 3 подходит.

Использование Scikit-learn

Мы видели, как выполнить первоначальную реализацию алгоритма, но во многих случаях вы можете захотеть встать на плечи гигантов и использовать другие проверенные и проверенные модули, которые помогут вам в работе по машинному обучению. В этом случае Scikit-learn — хороший выбор, и он имеет очень хорошую реализацию (k)-средних. Если вы хотите узнать больше об алгоритме и его оценке, вы можете взглянуть на главу 5 « Наука о данных и аналитика с помощью Python», где для обсуждения я использую набор данных Wine.

В этом случае мы покажем, как можно реализовать k-средние в нескольких строках кода, используя известный набор данных Iris. Мы можем загрузить его непосредственно из Scikit-learn и перетасовать данные, чтобы гарантировать, что точки не перечислены в каком-либо определенном порядке.

from sklearn.cluster import KMeans from sklearn import datasets from sklearn.utils import shuffle  # import some data to play with iris = datasets.load_iris() X = iris.data  y = iris.target names = iris.feature_names X, y = shuffle(X, y, random_state=42)

Мы можем вызвать реализацию KMeans, чтобы создать экземпляр модели и подогнать ее. Параметр n_clusters — это количество кластеров (k). В примере ниже мы запрашиваем 3 кластера:

model = KMeans(n_clusters=3, random_state=42)  iris_kmeans = model.fit(X)

Вот и все! Мы можем посмотреть на метки, предоставленные алгоритмом, следующим образом:

iris_kmeans.labels_

array([1, 0, 2, 1, 1, 0, 1, 2, 1, 1, 2, 0, 0, 0, 0, 1, 2, 1, 1, 2, 0, 1,        0, 2, 2, 2, 2, 2, 0, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1, 0,        0, 1, 1, 2, 1, 2, 1, 2, 1, 0, 2, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0,        1, 2, 0, 1, 1, 0, 1, 1, 1, 1, 2, 1, 0, 1, 2, 0, 0, 1, 2, 0, 1, 0,        0, 1, 1, 2, 1, 2, 2, 1, 0, 0, 1, 2, 0, 0, 0, 1, 2, 0, 2, 2, 0, 1,        1, 1, 1, 2, 0, 2, 1, 2, 1, 1, 1, 0, 1, 1, 0, 1, 2, 2, 0, 1, 2, 2,        0, 2, 0, 2, 2, 2, 1, 2, 1, 1, 1, 1, 0, 1, 1, 0, 1, 2], dtype=int32)

Для сравнения изменим порядок меток:

y = np.choose(y, [1, 2, 0]).astype(int) y

array([2, 1, 0, 2, 2, 1, 2, 0, 2, 2, 0, 1, 1, 1, 1, 2, 0, 2, 2, 0, 1, 0,        1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 1, 1, 0, 2, 1, 1, 1, 0, 2, 2, 1,        1, 2, 0, 0, 2, 0, 2, 0, 2, 1, 0, 2, 1, 1, 1, 2, 0, 1, 1, 1, 2, 1,        2, 0, 1, 2, 0, 1, 0, 0, 2, 2, 0, 2, 1, 2, 0, 1, 1, 2, 2, 1, 0, 1,        1, 2, 2, 0, 2, 0, 0, 2, 1, 1, 0, 0, 1, 1, 1, 2, 0, 1, 0, 0, 1, 2,        2, 0, 2, 0, 1, 0, 2, 0, 2, 2, 2, 1, 2, 2, 1, 2, 0, 0, 1, 2, 0, 0,        1, 0, 1, 2, 0, 0, 2, 0, 2, 2, 0, 0, 1, 2, 0, 1, 2, 0])

Мы можем проверить, сколько наблюдений было правильно назначено. Делаем это с помощью матрицы путаницы:

from sklearn.metrics import confusion_matrix conf_matrix=confusion_matrix(y, iris_kmeans.labels_)   fig, ax = plt.subplots(figsize=(7.5, 7.5)) ax.matshow(conf_matrix, cmap=plt.cm.Blues, alpha=0.3) for i in range(conf_matrix.shape[0]):     for j in range(conf_matrix.shape[1]):         ax.text(x=j, y=i,s=conf_matrix[i, j], va='center',                  ha='center', size='xx-large')   plt.xlabel('Predictions', fontsize=18) plt.ylabel('Actuals', fontsize=18) plt.title('Confusion Matrix', fontsize=18) plt.show()

Как мы видим, большинство наблюдений были правильно идентифицированы. В частности, кажется, что все из кластера 1 были захвачены.

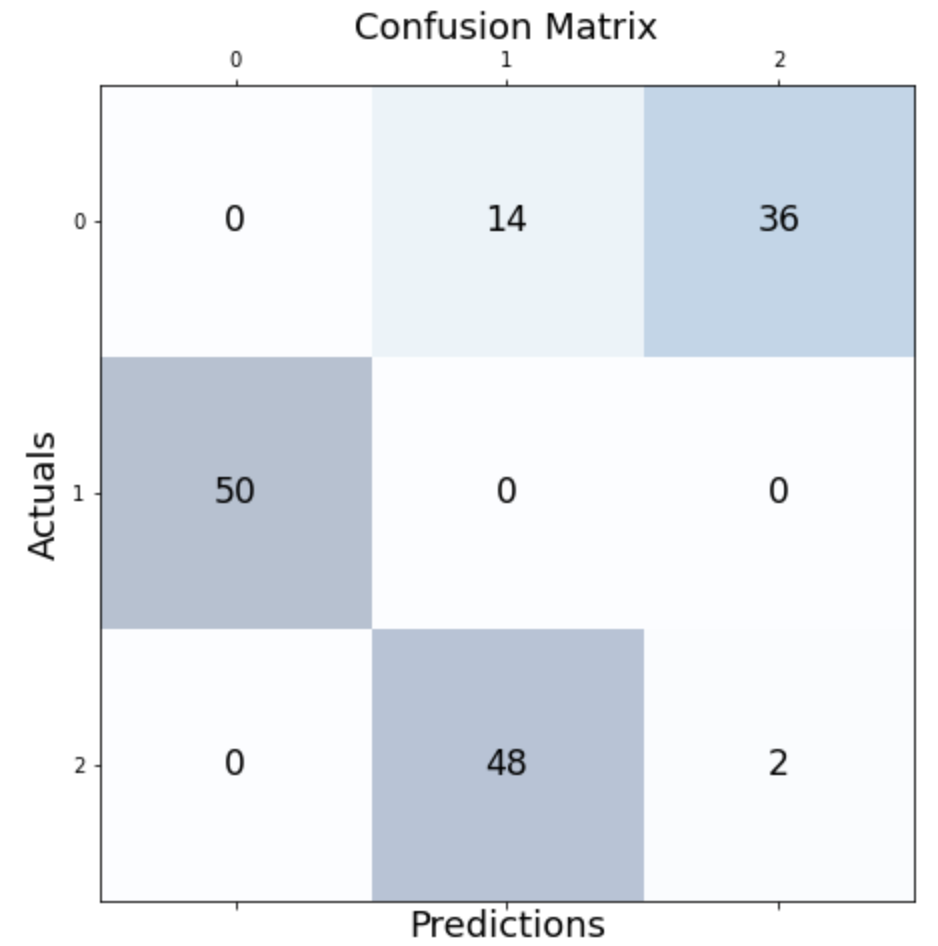
Давайте посмотрим на расположение финальных кластеров:

iris_kmeans.cluster_centers_

array([[5.006     , 3.428     , 1.462     , 0.246     ],        [5.9016129 , 2.7483871 , 4.39354839, 1.43387097],        [6.85      , 3.07368421, 5.74210526, 2.07105263]])

И мы можем посмотреть на 3D-графику. В этом случае мы построим следующие характеристики:

• Ширина лепестка
• Длина чашелистика
• Длина лепестка

Как видите, есть несколько наблюдений, которые различаются по цвету на двух графиках.

fig = plt.figure(figsize=(20, 10)) ax1 = fig.add_subplot(1, 2, 1, projection='3d') ax1.scatter(X[:, 3], X[:, 0], X[:, 2],              c=iris_kmeans.labels_.astype(float),             edgecolor="k", s=150, cmap=customcmap) ax1.view_init(20, -50) ax1.set_xlabel(names[3], fontsize=12) ax1.set_ylabel(names[0], fontsize=12) ax1.set_zlabel(names[2], fontsize=12) ax1.set_title("K-Means Clusters for the Iris Dataset", fontsize=12)  ax2 = fig.add_subplot(1, 2, 2, projection='3d')  for label, name in enumerate(['virginica','setosa','versicolor']):     ax2.text3D(         X[y == label, 3].mean(),         X[y == label, 0].mean(),         X[y == label, 2].mean() + 2,         name,         horizontalalignment="center",         bbox=dict(alpha=0.2, edgecolor="w", facecolor="w"),     )  ax2.scatter(X[:, 3], X[:, 0], X[:, 2],              c=y, edgecolor="k", s=150,              cmap=customcmap) ax2.view_init(20, -50) ax2.set_xlabel(names[3], fontsize=12) ax2.set_ylabel(names[0], fontsize=12) ax2.set_zlabel(names[2], fontsize=12) ax2.set_title("Actual Labels for the Iris Dataset", fontsize=12) fig.show()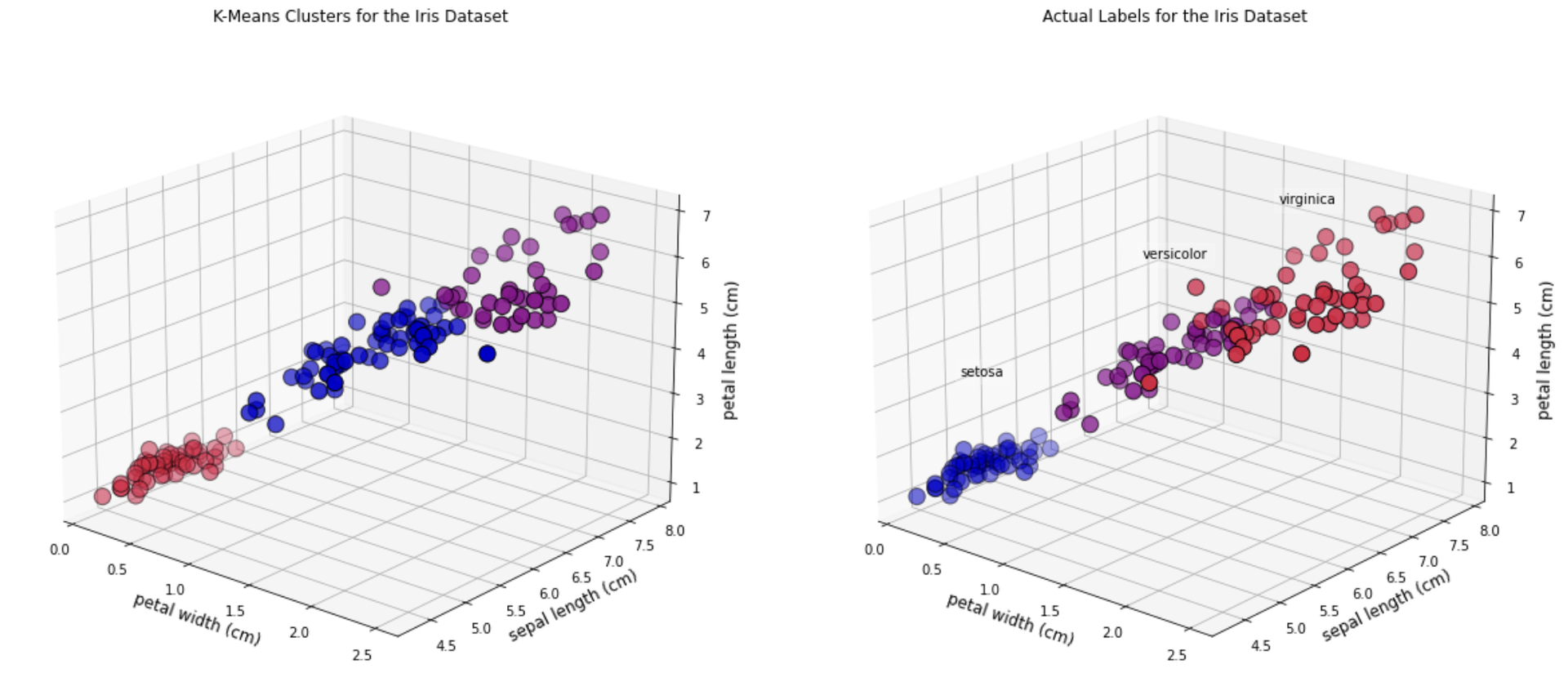

Краткое содержание

В этом посте мы объяснили идеи, лежащие в основе алгоритма (k)-средних, и предоставили простую реализацию этих идей на Python. Надеюсь, вы согласны с тем, что это очень простой для понимания алгоритм, и если вы захотите использовать более надежную реализацию, Scikit-learn поможет нам. Учитывая свою простоту, (k)-means является очень популярным выбором для начала кластерного анализа.

Источник: domino.ai

Комментарии: