Метод Монте-Карло — один из самых полезных алгоритмов в ИТ

Сегодня сложная тема, но мы объясним её просто и понятно. Разговор пойдёт про алгоритмы и немного про математику. 

Методы Монте-Карло — это набор методов в математике для изучения случайных процессов. Случайных — это когда что-то в них происходит непредсказуемым образом, например:

• подбрасываем монетку;
• кидаем кубик;
• опускаем жетоны в ячейки со столбиками;
• ловим элементарные частицы;
• считаем столкновения молекул;
• и что угодно ещё, что происходит полностью случайно и что нельзя предсказать заранее.

Смысл методов Монте-Карло в том, чтобы использовать данные случайных событий, чтобы на их основе получить более-менее точные результаты каких-то других вычислений. Они не будут идеально и математически точными, но их уже будет достаточно, чтобы с ними полноценно работать. Иногда это проще и быстрее, чем считать всё по точным формулам.

Пример такого вычисления — построение маршрута в навигаторе. В исходном виде это задача коммивояжёра, которая требует колоссальных вычислительных ресурсов. Но благодаря приближённым методам с ней справится даже не самый мощный телефон. Один из таких методов — метод Монте-Карло.

Как автомобильный навигатор находит самый быстрый путь

В чём идея метода

Если совсем примитивно, то работает так: 

Вместо того чтобы строить сложную математическую модель, мы берём простую формулу и пуляем в неё случайные числа. Считаем результат по каждому числу и получаем результат с нужной нам точностью. Чем больше случайных чисел — тем точнее результат. 

Вот то же самое немного подробнее:

1. Выбираем, что мы хотим найти или посчитать — значение формулы, площадь, объём, распределение материала или что-то ещё.
2. Смотрим, как это считается в математике, и находим нужные формулы.
3. На основе формул составляем критерий проверки — если случайное значение попало в этот критерий, мы его учитываем как совпавшее число, а если не попало — как не совпавшее.
4. Запускаем алгоритм, который выдаёт случайные числа, и проверяем каждое по этому критерию.
5. Как наберётся достаточное количество случайных чисел — считаем результат. Обычно это соотношение чисел, которые попали в критерий и которые не попали.

Чем больше будет случайных чисел — тем точнее результат. 

Плюс этого метода в том, что нам не нужно запрягать весь математический аппарат для решения задачи — достаточно подставлять числа в формулу и смотреть, получилось верное значение или нет.

Как найти число пи методом Монте-Карло

Для примера покажем классическое использование метода Монте-Карло — найдём число пи. Для этого нам понадобится круг, вписанный в квадрат, причём у круга радиус будет равен 1. Это значит, что сторона квадрата равна 2 — это диаметр (или два радиуса) круга:

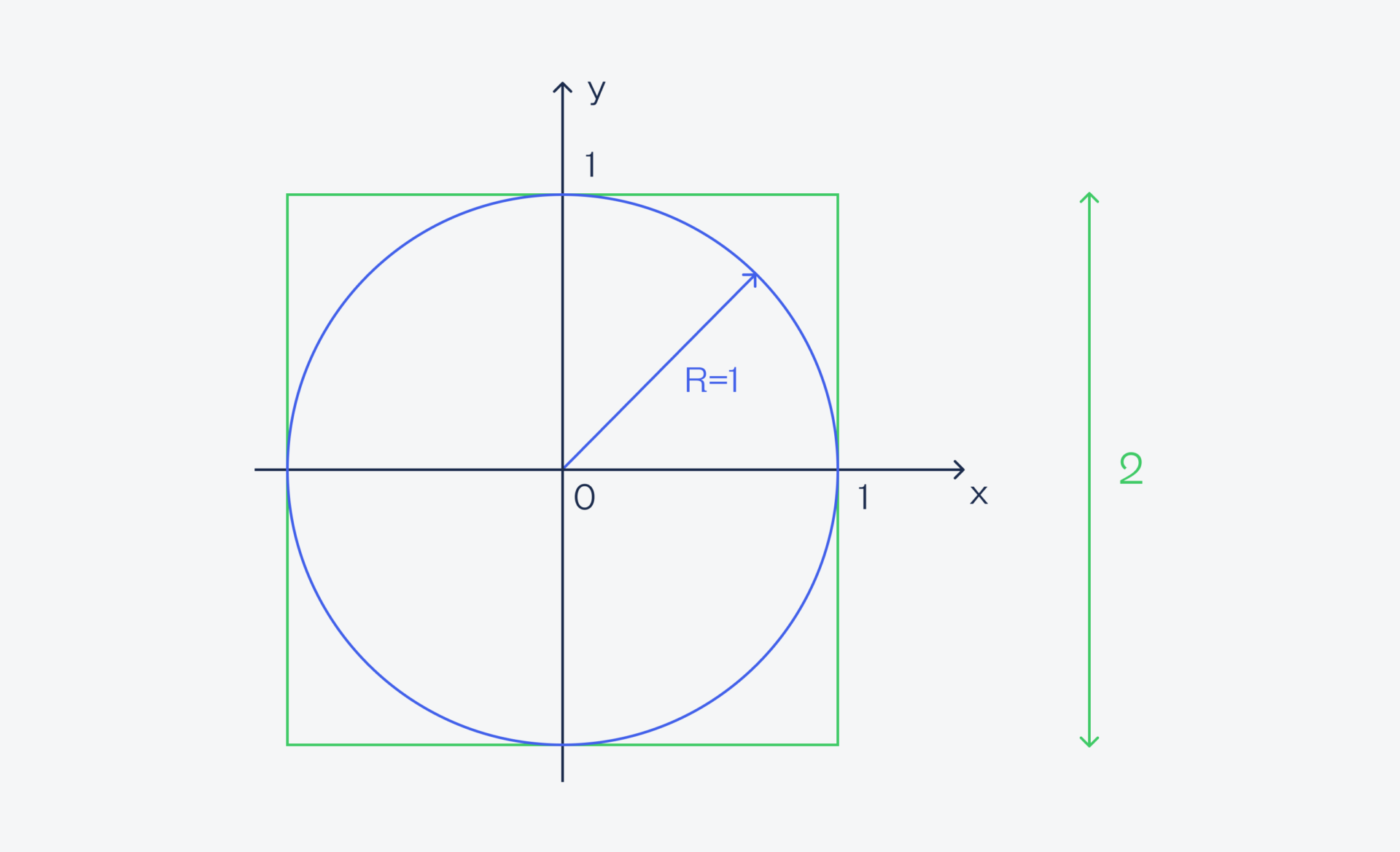
В этот квадрат мы будем случайным образом кидать песчинки и смотреть, попадут они в круг или нет (но останутся в границах квадрата). Исходя из этого набора данных мы можем посчитать отношение всех песчинок, которые попали в круг, ко всем песчинкам.

Теперь смотрим на формулы: 

• площадь квадрата со стороной 2 равна четырём;
• площадь круга радиусом 1 равна ?R? ? ??1? = ?.

Если мы разделим площадь круга на площадь квадрата, то получим ? / 4. Но мы ещё не можем по условию посчитать площадь круга, потому что мы не знаем число ?. Вместо этого мы можем разделить количество одних песчинок на другие — в этом и суть метода Монте-Карло. 

Это соотношение даст нам результат — ? / 4. Получается, что если мы умножим этот результат на 4, то получим число ?, причём чем больше песчинок мы кинем, тем точнее будет результат.

Кидать песчинки будем так: в качестве координат попадания X и Y будем брать случайные числа от 0 до 1. Это значит, что все числа попадут только в один квадрант — правый верхний:

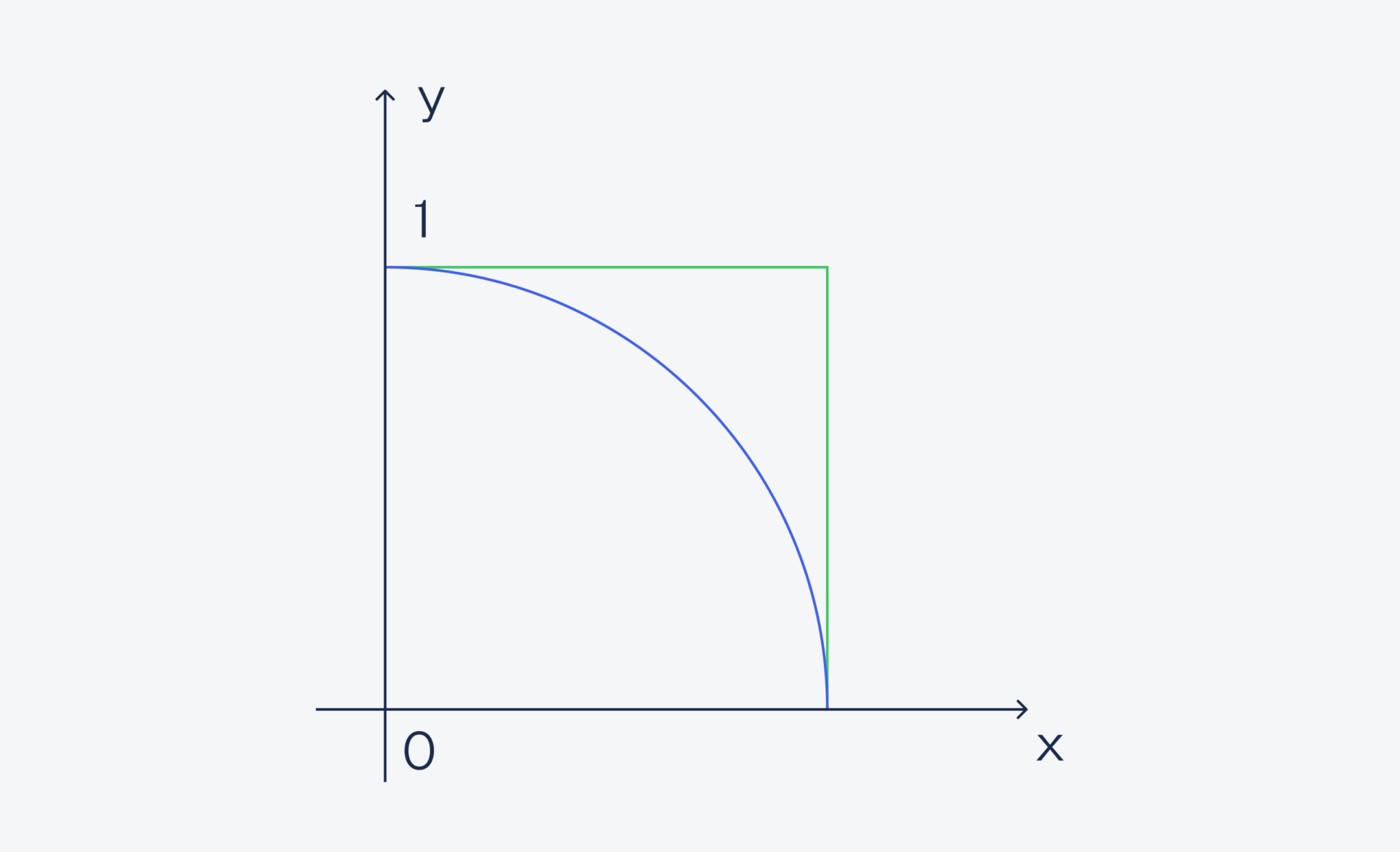
Но так как в этом квадранте ровно четверть круга и ровно четверть квадрата, то соотношение промахов и попаданий будет таким же, как если бы мы бросали песчинки в целый круг и целый квадрат.

Чтобы проверить, попадает ли песчинка в круг, используем формулу длины гипотенузы: x? + Y? = 1 (так как гипотенуза — это радиус окружности):

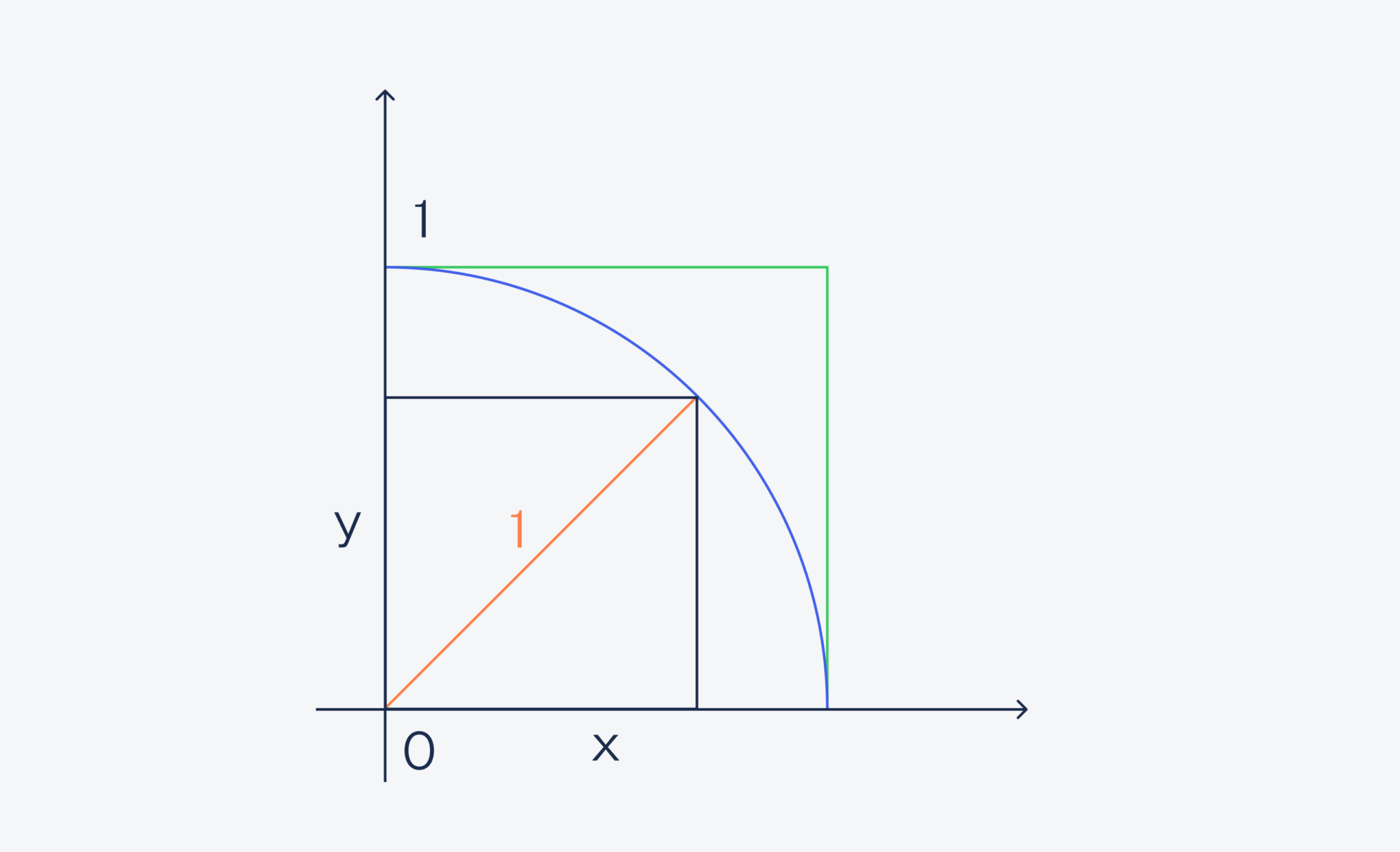
Если длина гипотенузы меньше единицы — точка попадает в круг. В итоге мы посчитаем и общее количество точек, и точек, которые попали в круг. Потом мы разделим одно на другое, умножим результат на 4 и получим приближённое значение числа ?.

Программируем поиск числа пи по методу Монте-Карло

Алгоритм на языке Python, читайте комментарии, чтобы лучше разобраться в происходящем:

# подключаем модуль случайных чисел import random   # функция, которая посчитает число пи def count_pi(n): 	# общее количество бросков     i = 0 	# сколько из них попало в круг     count = 0     # пока мы не дошли до финального броска     while i < n:         # случайным образом получаем координаты x и y         x = random.random()         y = random.random()         # проверяем, попали мы в круг или нет         if (pow(x, 2) + pow(y, 2)) < 1: 			# если попали — увеличиваем счётчик на 1             count += 1 		# в любом случае увеличиваем общий счётчик         i += 1     # считаем и возвращаем число пи     return 4 * (count / n)   # запускаем функцию pi = count_pi(1000000) # выводим результат print(pi)

Где ещё используется метод Монте-Карло

На методах Монте-Карло основано много полезного:

• моделирование облучения твёрдых тел ионами в физике;
• моделирование поведения разреженных газов
• исследования поведения разных тел при столкновении
• алгоритмы оптимизации и нахождения кратчайшего пути решения
• решение сложных интегралов (или когда их очень много)
• предсказание астрономических наблюдений
• поиск в дереве в различных алгоритмах
• алгоритмы работы некоторых функций квантового компьютера
• моделирование состояния приближённой физической среды

Без них изучать современный мир и совершать новые открытия было бы сложнее.