Линейный дискриминантный анализ (LDA). Принцип работы и реализация с нуля на Python

Линейный дискриминантный анализ (Linear Discriminant Analysis или LDA) — алгоритм классификации и понижения размерности, позволяющий производить разделение классов наилучшим образом. Основная идея LDA заключается в предположении о многомерном нормальном распределении признаков внутри классов и поиске их линейного преобразования, которое максимизирует межклассовую дисперсию и минимизирует внутриклассовую. Другими словами, объекты разных классов должны иметь нормальное распределение и располагаться как можно дальше друг от друга, а одного класса — как можно ближе.

Ноутбук с данными алгоритмами можно загрузить на Kaggle (eng) и GitHub (rus).

Не смотря на наличие логистической регрессии, в ряде случаев LDA может быть более предпочтительным вариантом по нескольким причинам:

• поскольку LDA основан на моделировании распределения данных в каждом классе, ему требуется меньше параметров для оценки, что уменьшает склонность к переобучению;

• при большом количестве классов и их хорошем линейном разделении является более стабильным и эффективным;

• может быть использован для понижения размерности без применения дополнительных методов.

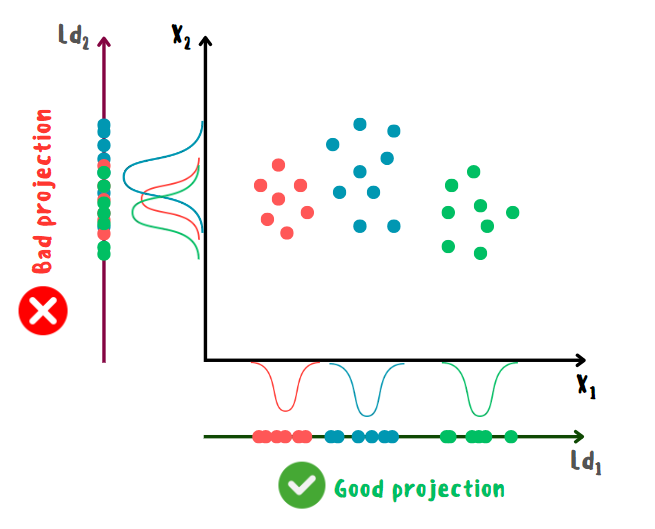
Принцип работы LDA

Алгоритм строится следующим образом:

• 1) изначально для всех классов рассчитываются априорные вероятности и средние значения признаков;

• 2) на основе полученных значений рассчитываются (ковариационные) матрицы разброса между классами и внутри классов;

• 3) далее находятся собственные вектора и значения для линейного дискриминанта Фишера, который определяется отношением матриц из шага 2;

• 4) собственные вектора сортируются в порядке убывания в соответствии с собственными значениями и называются дискриминантными векторами, с помощью которых рассчитываются веса модели;

• 5) на основе полученных весов и априорных вероятностей рассчитывается вектор смещения;

• 6) новое пространство признаков меньшей размерности представляет из себя линейную комбинацию исходных признаков и дискриминантных векторов и называется дискриминантным подпространством;

• 7) спрогнозированные классы являются максимальной оценкой линейной комбинации тестовой выборки и весов + смещение.

Формулы для расчётов

Среднее значение признаков по классу:

Среднее значение среди признаков:

Ковариационная матрица внутри класса:

Ковариационная матрица между классами:

Правило поиска собственных векторов и значений:

Веса модели:

Смещение модели:

Итоговый прогноз:

Где:

• и собственные вектора и значения соответственно;

• априорная вероятность класса k;

• дискриминантные вектора.

Более продвинутые техники

Помимо решения через нахождение собственных векторов, существуют также и другие подходы:

• использование сингулярного разложения, которое лучше подходит для данных с большим количеством признаков так как не вычисляется ковариационная матрица;

• решение методом наименьших квадратов, основанное на минимизации среднеквадратичной суммы отклонений по классам.

Помимо классического LDA, ещё существуют модификации на его основе, способные значительно не только улучшить качество модели, но и увеличить количество задач, в которых его можно применить. Наиболее популярными модификациями являются следующие:

• Квадратичный дискриминантный анализ (QDA) — это обобщение LDA, позволяющее каждому классу иметь собственную ковариационную матрицу. Это делает границу решения нелинейной и более гибкой, но также требует больше параметров для оценки.

• Гибкий дискриминантный анализ (FDA) — метод, который использует сглаживающие сплайны для построения нелинейных комбинаций признаков. Он может лучше аппроксимировать сложные зависимости между признаками и классами, но также может быть подвержен переобучению.

• Ядерный дискриминантный анализ (KDA) — метод отображения данных в пространстве более высокой размерности с использованием ядерного трюка (его суть объяснена в алгоритме SVM), где улучшается их линейная разделимость. Он также может улавливать сложные нелинейные зависимости, но требует выбора подходящего ядра и его параметров.

Стоит также отметить, что в LDA и его модификациях поддерживается регуляризация через степень сжатия ковариационной матрицы, которая регулируется с помощью параметра shrinkage (0 — отсутствие сжатия, 1 — полное сжатие). Сжатие ковариационной матрицы подразумевает увеличение её диагональных элементов и уменьшение внедиагональных. Такой подход добавляет штраф к модели за большие значения её параметров, что в целом повышает устойчивость и снижает риск переобучения. Также можно установить значение "shrinkage=auto", которое автоматически определяет оптимальный уровень сжатия с помощью леммы Ледуа-Вольфа.

Импорт необходимых библиотек

import numpy as np import pandas as pd import matplotlib.pyplot as plt from scipy.linalg import eigh as sp_eigh from sklearn.preprocessing import LabelEncoder from sklearn.metrics import accuracy_score from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from mlxtend.plotting import plot_decision_regions

Реализация на Python с нуля

class LDA:     def __init__(self, n_components=None):         self.n_components = n_components      def fit(self, X, y):         n_samples, n_features = X.shape         classes, cls_counts = np.unique(y, return_counts=True)         priors = cls_counts / n_samples          X_cls_mean = np.array([X[y == cls].mean(axis=0) for cls in classes])         between_cls_deviation = X_cls_mean - X.mean(axis=0)         within_cls_deviation = X - X_cls_mean[y]          Sb = priors * between_cls_deviation.T @ between_cls_deviation         Sw = within_cls_deviation.T @ within_cls_deviation / n_samples         evals, evecs = sp_eigh(Sb, Sw)         self.dvecs = evecs[:, np.argsort(evals)[::-1]]   # discriminant vectors          self.weights = X_cls_mean @ self.dvecs @ self.dvecs.T         self.bias = np.log(priors) - 0.5 * np.diag(X_cls_mean @ self.weights.T)          if self.n_components is None:             self.n_components = min(classes.size - 1, n_features)      def transform(self, X):         return X @ self.dvecs[:, : self.n_components]      def predict(self, X_test):         scores = X_test @ self.weights.T + self.bias          return np.argmax(scores, axis=1)

Загрузка датасета

Для обучения моделей будет использован Star Type Classification / NASA dataset, где необходимо определить тип звёзд на основе их признаков.

df_path = "/content/drive/MyDrive/star_type.csv" star_type = pd.read_csv(df_path) print(star_type.head())  X1, y1 = star_type.iloc[:, :-1], star_type.iloc[:, -1] cat_features_list = X1.select_dtypes(include=['object']).columns X1[cat_features_list] = X1[cat_features_list].apply(LabelEncoder().fit_transform)  X1, y1 = X1.values, LabelEncoder().fit_transform(y1) X1_train, X1_test, y1_train, y1_test = train_test_split(X1, y1, random_state=0)      Temperature         L       R    A_M Color Spectral_Class  Type 0         3068  0.002400  0.1700  16.12   Red              M     0 1         3042  0.000500  0.1542  16.60   Red              M     0 2         2600  0.000300  0.1020  18.70   Red              M     0 3         2800  0.000200  0.1600  16.65   Red              M     0 4         1939  0.000138  0.1030  20.06   Red              M     0

Обучение моделей и оценка полученных результатов

LDA показал лучший результат в сравнении с логистической регрессией, классифицировав правильно абсолютно все звёзды, что в данном случае возможно благодаря учёту различий в дисперсии признаков между классами. Подобные примеры хорошо показывают, что выбор подходящего алгоритма под определённые данные даже более важен настройки его параметров. Проще говоря, для получения хороших результатов далеко не всегда стоит применять сложные и более продвинутые алгоритмы.

В конце также приведены графики границ решений для LDA, обученном на исходных и преобразованных данных.

LDA

lda = LDA() lda.fit(X1_train, y1_train) lda_pred_res = lda.predict(X1_test) transformed = lda.transform(X1_train) lda_accuracy = accuracy_score(y1_test, lda_pred_res)  print(f'LDA accuracy: {lda_accuracy}') print(f'prediction: {lda_pred_res}') print('Transformed features', transformed[:5].T, sep='
')   LDA accuracy: 1.0  prediction: [4 1 3 1 4 4 3 4 3 1 1 2 2 3 5 1 0 5 4 0 4 5 2 0 0 2 1 3 1 4 5 4 2 0 2 5 2  5 0 3 3 4 3 1 4 1 4 0 5 5 0 3 5 1 3 3 5 3 5 4]  Transformed features [[  6.55221495  -0.8571998    2.16465265 -11.03062098   7.62073549]  [  3.74443434  -1.09820125   1.2128982    8.75538862   3.88801176]  [  2.22462072   1.09291992  -0.73431527  -2.47258084  -0.96369278]  [ -2.78598515  -3.15408968  -4.37644643  -1.18437944  -0.47014263]  [  3.49749891   5.19757349   4.41467643   5.26540777   2.91398214]]

LDA (scikit-learn)

sk_lda = LinearDiscriminantAnalysis(solver='eigen') sk_lda.fit(X1_train, y1_train) sk_lda_pred_res = sk_lda.predict(X1_test) sk_transformed = sk_lda.transform(X1_train) sk_lda_accuracy = accuracy_score(y1_test, sk_lda_pred_res)  print(f'sk LDA accuracy: {sk_lda_accuracy}') print(f'sk LDA prediction: {sk_lda_pred_res}') print('sk transformed features', sk_transformed[:5].T, sep='
')   sk LDA accuracy: 1.0  sk LDA prediction: [4 1 3 1 4 4 3 4 3 1 1 2 2 3 5 1 0 5 4 0 4 5 2 0 0 2 1 3 1 4 5 4 2 0 2 5 2  5 0 3 3 4 3 1 4 1 4 0 5 5 0 3 5 1 3 3 5 3 5 4]  sk transformed features [[  6.55221495  -0.8571998    2.16465265 -11.03062098   7.62073549]  [  3.74443434  -1.09820125   1.2128982    8.75538862   3.88801176]  [  2.22462072   1.09291992  -0.73431527  -2.47258084  -0.96369278]  [ -2.78598515  -3.15408968  -4.37644643  -1.18437944  -0.47014263]  [  3.49749891   5.19757349   4.41467643   5.26540777   2.91398214]]

Logistic Regression (scikit-learn)

lr = LogisticRegression(max_iter=5000) lr.fit(X1_train, y1_train) lr_pred_res = lr.predict(X1_test) lr_accuracy = accuracy_score(y1_test, lr_pred_res)  print(f'sk logistic regression prediction: {lr_pred_res}') print(f'sk logistic regression accuracy: {lr_accuracy}')   sk logistic regression prediction: [4 1 3 1 4 4 3 4 3 1 1 2 2 3 5 1 0 5 4 0 4 5 2 0 0 2 1 3 1 4 5 4 2 0 2 5 2  5 0 3 3 4 3 1 4 1 4 0 5 5 0 3 5 1 2 3 5 3 5 4]  sk logistic regression accuracy: 0.9833333333333333

Визуализация прогнозов

feature_indexes = [3, 0] sk_lda1 = LinearDiscriminantAnalysis(solver='eigen') sk_lda1.fit(X1_train[:, feature_indexes], y1_train) plt.title('LDA surface with original features') plot_decision_regions(X=X1[:, feature_indexes], y=y1, clf=sk_lda1)

feature_indexes = [3, 0] sk_lda2 = LinearDiscriminantAnalysis(solver='eigen') X1_lda = sk_lda2.fit(X1, y1).transform(X1) X1_lda = X1_lda[:, feature_indexes] X1_lda_train, X1_lda_test, y1_train, y1_test = train_test_split(X1_lda, y1, random_state=0) sk_lda2.fit(X1_lda_train, y1_train) plt.title('LDA surface with transformed features') plot_decision_regions(X=X1_lda, y=y1, clf=sk_lda2)

Преимущества и недостатки LDA

Преимущества:

• простой и эффективный метод для линейной классификации и понижения размерности;

• учитывает различия между классами и внутри классов;

• хорошо работает, когда классы имеют нормальное распределение и одинаковую ковариационную матрицу.

Недостатки:

• требуется достаточного количества данных для каждого класса, чтобы оценить матрицы разброса;

• чувствителен к выбросам и нарушению предположений о нормальности и гомоскедастичности;

• может быть неэффективным, когда число признаков сильно превышает число объектов.

Дополнительные источники

Статья «Linear and Quadratic Discriminant Analysis: Tutorial», Benyamin Ghojogh, Mark Crowley.

Документация:

• описание дискриминантного анализа;

• LDA;

• QDA.

Видео: один, два, три, четыре.

Наивный Байес ?