Информация об информации. Энтропия Шеннона, демон Максвелла и предел Ландауэра

«Информация – величина физическая» (Рольф Ландауэр)

«Вся информация, которая существует, хранится физическими системами, и все физические системы хранят информацию» (Сет Ллойд)

«…слово «информация» в теории коммуникации относится не столько к тому, что вы говорите, сколько к тому, что вы могли бы сказать…».

«Человек, впервые сталкивающийся с понятием энтропии в теории коммуникаций, вправе ощутить волнение, он вправе заключить, что встретил нечто основополагающее, важное» (Уоррен Уивер)

Что такое информация? Пожалуй, каждый ответит на этот вопрос по-своему. Для гуманитария информация – это любые сведения, которые можно запомнить и передать в устной или письменной форме. Для физика-теоретика информация – это набор квантовых чисел, характеризующих состояние элементарной частицы. Для программиста информация – это цифровые данные, которые можно представить в двоичном коде и измерить в битах. Единого определения информации в науке до сих пор нет, что способствует распространению сомнительных толкований термина. Зачастую словом «информация» в силу его многозначности прикрывают всю массу недопонятых или ещё не до конца изученных явлений, или же используют его как лазейку для паранормального, когда нечто не получается описать физическими категориями. Например, эзотерики считают информацию некой метафизической субстанцией или связывают её с нематериальными «тонкими» мирами, философы-идеалисты отождествляют её с духом и сознанием, квантовые мистики используют словосочетание «информационное поле». Утверждается, что информация нефизична, неизмерима и нелокальна, что она не подчиняется законам сохранения и может передаваться быстрее скорости света. Как же измерить неисчислимое и определить неосязаемое? Или может быть информация – совсем не то, что мы обычно подразумеваем под этим словом?

Что такое информация?

Этимологически слово «информация» происходит от латинского informare «придавать форму, воображать, представлять» и означает «разъяснение», «понятие о чём-либо». В международной системе стандартов ISO/IEC информация определена как «знания относительно фактов, событий, вещей, идей и понятий, которые в определённом контексте имеют конкретный смысл». «Хотя информация должна обрести некоторую форму представления, чтобы ею можно было обмениваться, информация есть в первую очередь интерпретация такого представления». То есть физическая форма представления (presentation) – это одно, а содержание или смысл представления (representation) – это другое. Но почему тогда мы обозначаем одним и тем же словом разные вещи? Форма представления – это просто последовательность знаков, а смысл – это закодированные знаками идеи, образы, математические объекты и т.д. Но смысл – вещь субъективная и не поддающаяся количественной оценке. Поэтому его традиционно изучает такая «гуманитарная» наука как семантика, а естественные науки рассматривают информацию как абстрактное математическое понятие, безотносительно к её семантическому аспекту.

В философии информации тоже не всё так однозначно. С одной стороны, информация определяется как «универсальное свойство материи», «мера организованности системы», «одно из свойств предметов, явлений, процессов объективной действительности», «отрицание энтропии» (Бриллюэн), «мера сложности структур» (Моль), «снятая неразличимость, передача разнообразия, мера изменения во времени и пространстве структурного разнообразия систем» (Эшби). С другой стороны, информация субъективна, т.е. существует только в нашем сознании – это «сведения, воспринимаемые человеком», «отражение в сознании людей объективных причинно-следственных связей», «содержание процессов отражения» (Тузов), «отражённое разнообразие» (Урсул), «вероятность выбора» (Яглом), «снятая неопределённость» (Шеннон), «то, что способно информировать» (Википедия).

«Информация – это обозначение содержания, полученное нами из внешнего мира в процессе приспособления к нему нас и наших чувств» (Норберт Винер)

«Информация – это не знание само по себе, а значение, которое может быть получено из представления посредством интерпретации» (Хьюберт Йоки)

Очевидно, понятие информации нуждается в переосмыслении и более строгом определении. Что же делать? На первый взгляд, лучшее решение – выбрать самое общее и абстрактное определение, которое будет включать в себя все остальные. Часто можно услышать простые определения одним словом, например: информация – это сведения, данные, биты, значение, представление, понимание, знание и т.д. Но все эти понятия определяются одно через другое и образуют замкнутый логический круг. Другое решение – найти какое-то общее свойство, присущее информации. Как пишет Сет Ллойд в книге «Программируя Вселенную», «основная идея информации состоит в том, что одну физическую систему – цифру, букву, слово, предложение – можно поставить в соответствие другой физической системе». Да, и не обязательно физической: буквы и цифры могут также символизировать абстрактную математическую сущность. Тогда информация – это символическое представление одной сущности с помощью другой. Но сама информация не является абстрактной в том же смысле, что и множество всех простых чисел, поскольку она существует только тогда, когда она физически реализована.

Я дам своё определение информации в конце статьи, а пока для простоты понимания материала будем называть информацией всё, что может быть представлено как строка битов – нулей и единиц. Фактически любой материальный объект или физический процесс можно оцифровать и смоделировать на универсальном компьютере. Конечно, в случае с квантовыми системами это потребует колоссальных вычислительных ресурсов, и гораздо проще было бы моделировать их на квантовом компьютере, который является аналоговой машиной. О квантовой информации я уже писал в статье «Квантовый компьютер» и буду подробнее писать в дальнейшем. А в данной статье речь пойдёт только о классической информации, которая возникает на макроскопических масштабах и является предметом изучения теории информации. Я собираюсь показать, что информация во всех её проявлениях – вполне физическая, объективная, измеряемая величина, в которой нет ничего субъективного и мистического. Но сначала пройдём вводный курс по основам информатики и разберёмся, что такое энтропия по Шеннону.

Информация в информатике

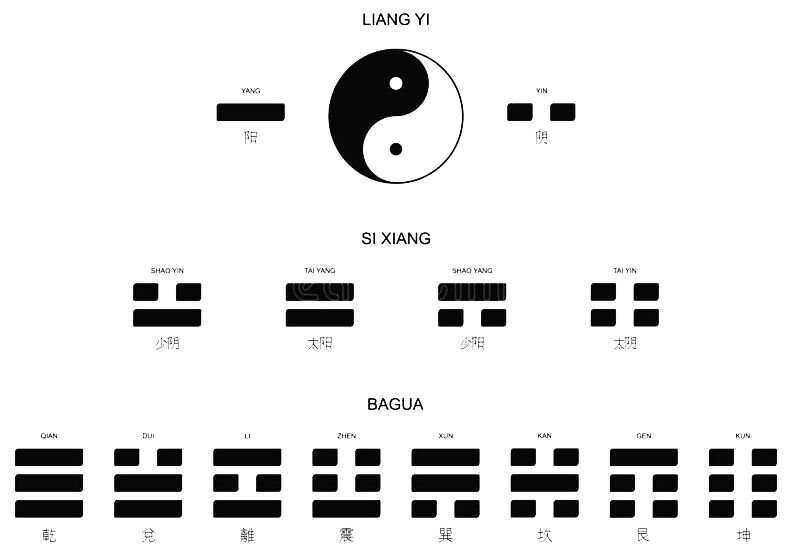
Предтечей информатики считается немецкий математик Готфрид Лейбниц, который придумал двоичную систему счисления, оперирующую только нулями и единицами (1703), а также изобрёл прототипы перфокарты и двоичного калькулятора. Однако сам Лейбниц в своей работе «Объяснение двоичной арифметики» писал, что двоичный разряд уже использовал за 4000 лет до него китайский император и философ Фу Си. Сегодня китайский бит хорошо известен как инь-ян, но были ещё двубит (сы-сян) и трибит (ба-гуа). Последний образовывал восемь триграмм, из которых состоят 64 гексаграммы книги Перемен, соответствующие двоичным числам от 0 до 111111. Но всё же вычислительная техника получила развитие не в Китае, а в Европе во время промышленной революции. В середине XIX в. перфокарты стали применять в ткацких станках, а Чарльз Бэббидж разработал проект механического компьютера – «дифференциальной машины». В 1911 г. была основана компания IBM, использовавшая перфокарты для статистических расчётов и впоследствии спроектировавшая первый программируемый калькулятор. В 1937 г. американский инженер Клод Шеннон защитил диссертацию, в которой показал, что любые объекты и взаимодействия между ними можно выразить последовательностями нулей и единиц, а любые логические задачи можно решать с помощью организации электромеханических реле. Тем самым он заложил основы теории информации и предпосылки для построения аналоговых вычислительных машин.

Информатика как наука занимается изучением законов формирования, преобразования и распространения информации в природе. Она работает исключительно с данными, то есть информацией, представленной в цифровой форме, пригодной для обработки человеческим мозгом или компьютером. Такая информация всегда связана с материальным носителем. Она может быть записана для хранения на вещественных носителях вроде электронных транзисторов, бумаги, кодонов ДНК или нейронов мозга, а может передаваться в пространстве в виде сигнала, переносимого звуковыми или электромагнитными волнами. Есть два способа кодирования информации: аналоговый (если носитель может передавать непрерывный ряд значений) и цифровой (если носитель принимает дискретный ряд значений). Независимо от носителя сама информация всегда дискретна, то есть состоит из конечного числа знаков (символов).

Совокупность символов, необходимая для передачи той или иной информации, называется сообщением. Чтобы знаки считались информацией, они должны однозначно считываться и копироваться при помощи устройства, способного измерить характеристики физического носителя информации, распознать в них знаки и скопировать их на другой носитель. Если мы хотим кому-то передать информацию, её нужно сначала закодировать (устными словами, жестами, мимикой или символами – написанными от руки, напечатанными и т.д., хоть азбукой Морзе) и затем послать сообщение по каналу передачи (звуковыми волнами по воздуху, фотонами видимого света, электрическими импульсами по телефонной линии, радиоволнами по спутниковой связи, через интернет и т.д.), причём желательно без ошибок, а получатель должен обработать информацию (не просто услышать или увидеть, но и расшифровать, понять, принять к сведению) и как-то прореагировать (ответить, запросить уточнение, проигнорировать и т.д.).

Теория информации

Теория информации, она же теория коммуникаций, она же математическая теория связи, возникла чисто из практических потребностей: в эпоху электроники инженерам и математикам нужно было как-то определить и измерить то, что они пересылали по линиям связи, транслировали в радиопередачах, хранили на перфокартах и обрабатывали в процессорах. В ходе работы у них возникали вопросы: как лучше хранить и передавать данные, чтобы свести к минимуму ошибки из-за несовершенства материалов и неизбежных изменений в физических устройствах или каналах связи? Сколько нужно дополнительной памяти, чтобы обеспечить эту безошибочность? Как быстро можно передавать информацию по каналу связи, зная его пропускную способность и уровень помех? С технической точки зрения теория информации была инструментом, который помогал выяснить, каким образом шумы в форме случайных помех препятствуют плавному потоку битов при передаче. Она подсказывала способ определения необходимой пропускной способности каналов связи, компакт-дисков и прочих технологий, кодировавших язык, звуки и зрительные образы. И она указывала пути исчисления эффективности различных схем коррекции ошибок, в частности применения некоторых битов для проверки остальных.

В теории информации понятие информации до сих пор отсутствует, но есть такие термины, как «источник информации», «среда распространения информации (канал связи)» и «получатель (приёмник) информации», а также единица измерения информации – бит. Слово «бит» (от BInary digit – «двойное число» или «бинарный выбор») придумал в 1946 г. американский учёный-статистик Джон Тьюки. 1 бит – это один двоичный разряд, который может принимать значения «0» или «1». Любая информация сводится к последовательности элементарных выборов между двумя возможностями: вопросов, на которые можно ответить «да» или «нет». Сколько нужно задать вопросов, чтобы определить каждый следующий символ в сообщении? Наименьшее количество таких вопросов – мера извлекаемой информации. Один бит – то, что уменьшает неопределённость вдвое.

В статье Андрея Колмогорова «Три подхода к определению понятия количества информации» (1965) рассматриваются три способа измерения информации: комбинаторный (информация по Хартли), вероятностный (энтропия Шеннона) и алгоритмический (колмогоровская сложность). Комбинаторный подход был сформулирован в 1920-х гг. в работах Гарри Найквиста и Ральфа Хартли. По формуле Хартли, количество информации равно двоичному логарифму от числа возможных исходов какого-либо действия или события. Вероятность события обратно пропорциональна числу исходов, если они равновероятны. Например, у броска честной монеты есть два равновероятных исхода – «орёл» и «решка», обозначаемые соответственно «1» и «0», и каждый бросок будет содержать 1 бит информации. С двумя монетами можно получить уже четыре равновероятных комбинации (00, 01, 10, 11), энтропия броска – 2 бита. У броска игральной кости шесть исходов, для записи которых нужно уже три бита. Это значит, что нужно задать минимум 3 вопроса, чтобы узнать, какой стороной выпал кубик. У генератора случайных чисел вероятность появления каждого следующего символа – 1/10, соответственно информации здесь будет уже 4 бита.

Теперь возьмём три сообщения:

1. 00000000000000000000000000000000000000000000000000

2. 01010101010101010101010101010101010101010101010101

3. 01110010100001010111001000000110100010111010111001

Они занимают одинаковый объём памяти – 50 бит, а вот количество информации в них различается. В первом сообщении мы видим максимальную упорядоченность и предсказуемость, но информации в нём содержится минимум. Сообщение можно сжать до repeat (0), значит, количество информации равно всего 1 бит. Во втором сообщении можно заметить периодичность и сжать его до repeat (01), соответственно информации будет уже 2 бита. Наконец, в третьем случае сообщение похоже на случайную последовательность нулей и единиц. Единственный способ описать эту строку – указать каждую цифру, поэтому количество информации в ней максимально – 50 бит. Интуитивно кажется, что вероятность получить третью последовательность, бросая честную монету, намного выше, чем в случае с первыми двумя, ведь решка не может выпадать 50 раз подряд. Но на самом деле эти последовательности равновероятны, и получить их так же трудно, как и любую из 2⁵⁰ возможных комбинаций.

Как видно из этих примеров, информация имеет статистическую природу и выражает степень неопределённости в сообщении. Если вы читали статью «Правда и мифы об энтропии», вы уже знаете, что аналогичные характеристики имеет и другая величина – энтропия по Больцману. У них даже формулы подобны: термодинамическая энтропия пропорциональна логарифму возможных физических состояний, а количество информации пропорционально логарифму возможных исходов события. Энтропия облака пара выше, чем энтропия кубика льда, потому что в облаке есть гораздо больше способов расположить молекулы воды, чем в кристаллической решётке льда. Точно так же случайная последовательность символов имеет высокую энтропию, потому что допускает очень много способов расположения этих символов, а сообщение, подчиняющееся строгому шаблону, имеет низкую энтропию. 

Информационная энтропия

В 1948 г. Клод Шеннон, работавший инженером в лабораториях телефонной компании «Bell System», в своей статье «Математическая теория связи» впервые предложил использовать бит как единицу измерения информации. Также он описал канал связи как множество всевозможных шумов, а источник сообщений – как множество всех возможных сообщений. Но главное – Шеннон связал количество информации с вероятностью появления символа, и назвал эту величину информационной энтропией. Впоследствии он вспоминал:

«Меня больше всего беспокоило, как это назвать. Я думал назвать это «информацией», но это слово использовалось слишком часто, поэтому я решил назвать это «неопределённостью». Когда я обсуждал это с Джоном фон Нейманом, у него возникла идея получше. Фон Нейман сказал мне: «Вам следует называть это энтропией по двум причинам. Во-первых, ваша функция неопределенности использовалась в статистической механике под этим именем, поэтому у неё уже есть имя. Во-вторых, что более важно, никто на самом деле не знает, что такое энтропия, поэтому в дебатах у вас всегда будет преимущество».

Вероятностный подход Шеннона обобщает меру количества информации по Хартли на случай, когда не все элементы множества являются равнозначными, а также с учётом влияния шума в канале связи. Энтропия Шеннона оценивает среднее количество информации (математическое ожидание), которое содержится в значениях случайной величины. Согласно формуле Шеннона, информация, добавленная каждым новым символом – это логарифм от вероятности его появления, основание которого – количество символов в алфавите.

Клод Шеннон заметил, что информационная энтропия подчиняется следующим закономерностям:

А) Энтропия события равна 0, если его вероятность равна 1 (100%);

Б) Энтропия двух независимых событий равна сумме энтропий этих событий;

В) Энтропия максимальна, если все события равновероятны.

Получается, чем сложнее предсказать исход события, тем больше информации оно несёт. Если событие редкое и непредсказуемое, мы называем его новостью и наделяем информационной ценностью. Если же оно повторяется часто и о нём постоянно рассказывают, его информационная ценность теряется.

Что же такое энтропия по Шеннону? Мера неопределённости (непредсказуемости, неожиданности) появления символа. Мера равномерности распределения случайной величины. Среднее значение количества информации в сообщении. Количество информации, приходящейся на одно элементарное сообщение источника. Разница между информацией, содержащейся в сообщении, и той частью информации, которая точно известна в сообщении. Минимальное количество битов, необходимое для передачи сообщения. Средняя скорость, с которой производит информацию стохастический источник информации. Сумма взвешенных по вероятностям логарифмических вероятностей события. А информацию Шеннон определил как снятую неопределённость – результат выбора одного варианта из числа возможных, уменьшение количества рассматриваемых вариантов (разнообразия).

Есть мнение, что информация – это мера упорядоченности, регулярности или организованности. Но на самом деле формула Шеннона ясно показывает: чем больше в сообщении информации, тем более оно бессистемно. Например, наименее информативная картина будет похожа на «Чёрный квадрат» Малевича, наиболее информативная – на хаотичную разноцветную «живопись» искусственного интеллекта. В музыке минимум информации содержит звучание одной ноты, максимум – беспорядочная какофония. Если мы включим телевизор, минимальное количество информации будет передавать чёрный экран, максимальное – белый шум, имеющий одинаковую спектральную мощность на всех частотах. А идеальный порядок, регулярность и организованность соответствуют минимальному значению энтропии.

В любой строке кода какой-то процент данных составляет полезная информация, остальное – это «вода» или шум. Поэтому всё, что не является случайной последовательностью знаков, можно сжать. Чем более предсказуемы получаемые данные, тем лучше их можно сжать. Случайная независимая равновероятная последовательность битов сжатию без потерь не поддаётся. В интернете есть калькуляторы информационной энтропии, где вы можете ввести любой текст и вычислить его энтропию по Шеннону. Её можно использовать как показатель эффективности алгоритма сжатия: если вы далеки от этого числа, значит, можно найти алгоритм и получше, если же близки к нему, значит, добиться большего уже не получится. Энтропия Шеннона – фундаментальный предел, насколько мы можем сжать сообщение без риска искажения, т.е. максимально достижимые возможности кодирования без потерь. Если отправитель использует для передачи сообщения меньше битов, сообщение неизбежно будет искажено.

Энтропия естественного языка

Язык – это тоже своего рода программный код, позволяющий нам выражать свои мысли и чувства. Когда человек говорит или пишет, он является источником информации. Мы используем систему из 33-х символов, хотя их можно сократить до двух, используя азбуку Морзе. То же самое делает компьютер, когда переводит текст в понятные ему нули и единицы. В стандартной кодировке ASCII для записи каждой буквы алфавита или цифры требуется 8 бит (1 байт) информации. Но это неэкономно, поскольку буквы алфавита встречаются в тексте с разной частотой. По статистике, вероятность того, что взятой наугад буквой английского языка окажется буква «e», гораздо выше среднего значения 1/26, а для буквы «q» - гораздо ниже 1/26. Поэтому часто встречающиеся буквы кодируют меньшим количеством битов, а редко встречающиеся – большим. Например, у нас есть участок ДНК – последовательность нуклеотидов, обозначаемых символами А, Г, Ц и Т. Если эти буквы равновероятны (по 25%), энтропия будет максимальной, и мы сможем кодировать каждую из них минимум двумя битами: А – 00, Г – 01, Ц – 10, Т – 11. Но предположим, что А встречается с вероятностью 50%, Г – 30%, Ц и Т – по 10%. Тогда можно присвоить буквам коды переменной длины, чтобы получение единицы сообщало смотреть ещё один бит, если только мы не получили перед этим две последовательных единицы. Если закодировать А как 0, Г как 10, Ц как 110 и Т как 111, то половину времени мы будем посылать всего 1 бит, 30% времени – 2 бита и 20% времени – три бита. Экономия!

Кроме того, у каждого естественного языка есть своя грамматика, которая позволяет вычислить вероятность появления той или иной буквы в слове в зависимости от уже переданных символов. Последовательность случайных событий, в которой вероятность будущих исходов зависит от предыдущих, известна математикам как цепь Маркова. Она широко используется в алгоритмах байесовского вычисления, позволяющих среди прочего узнать условную энтропию. Например, в английском тексте за буквой «t» чаще всего следует буква «h» или «о», а идентификация уже двух букв позволяет строить дальнейшие догадки. По тому же принципу работают генеративные языковые модели, определяющие вероятность каждого следующего слова в токене на основе первоначального запроса и ранее сгенерированных слов. Как показал Шеннон, поток информации в обычном языке является менее чем случайным; каждый новый бит частично ограничен предшествующими; таким образом, каждый новый бит несет в себе в некоторой степени меньше содержания, чем тот, что заключает в себе реальную информацию. Чем выше доля случайности в потоке данных, тем больше информации будет передано каждым новым битом.

С помощью теории информации можно без потери смысла сократить количество букв в словах. Тогда мозг, основываясь на лимитированном количестве информации «урезанного» текста, будет сам достраивать отсутствующие элементы для восстановления смысла. Наглядный пример – всем известная реклама курсов стенографии «если в мжт прчть здс сбщн». Выходит, что все наши языки в той или иной степени избыточны, т. е. содержат звуки или буквы, которые не являются строго необходимыми для передачи сообщения. Клод Шеннон оценил избыточность английского языка в 75%. Согласно учебнику «Теория информации» Ерохина, русский язык избыточен на 73%, французский – на 71%, немецкий – на 66%. Внутри языка наименьшей избыточностью обладает живая речь, чуть большей – литературный текст, а наиболее избыточными (80-95%) являются юридические документы и язык диспетчеров аэропорта. Без избыточности мы не смогли бы разгадывать кроссворды, играть в слова и писать стихи. Если энтропия языка характеризует неопределённость и непредсказуемость появления следующей буквы или слова, то избыточность – наоборот, мера предопределённости, предсказуемое отклонение от случайного.

Избыточность

Избыточность – это превышение количества информации для передачи или хранения сообщения над его информационной энтропией. Проще говоря, чем избыточнее текст, тем больше в нём «воды». Избыточность необходима для того, чтобы передавать информацию без потерь по зашумлённому каналу. В мире, где невнятно проговаривают слова и допускают опечатки, надёжность связи существенным образом зависит от избыточности. Например, если QR-код наполовину стереть, сканер всё равно его прочитает, потому что он очень избыточен. Если какая-нибудь космическая частица изменит содержимое ячейки памяти компьютера, информации в соседних ячейках хватит, чтобы исправить эту ошибку. Избыточные элементы кода можно уподобить сминаемым зонам в кузове автомобиля: в случае аварии они принимают на себя силу удара, чтобы салон с пассажирами остался целым. Аналогичную функцию выполняют «мусорные» части ДНК и теломеры хромосом, которые укорачиваются при каждом делении клетки, предотвращая ошибки в копировании кода.

Если же вы уверены в надёжности канала связи, но хотите максимально сократить объём сообщения, тогда вам в помощь алгоритмы сжатия данных – энтропийное кодирование. Например, архиваторы переписывают код так, что часто встречающиеся символы обозначаются меньшим количеством битов, а редко встречающиеся – большим. То же самое происходит при переводе картинки из формата .bmp или .png в формат .jpg. Любое изображение состоит из отдельных пикселей, а в них можно обнаружить закономерности и сжать объём данных в несколько раз. Важно понимать, что архиваторы не удаляют избыточную информацию, а приводят файл к максимально хаотичному (высокоэнтропийному) состоянию, уменьшая объём памяти, необходимой для его хранения. Но информация как таковая сохраняется, что делает возможным обратный процесс разархивирования. Долю избыточности («воды») можно сжимать, пока в сообщении не останется чистая информация (энтропия), которая постоянна и не убывает, что бы мы ни делали. Это напоминает обратимый адиабатический процесс в термодинамике и гравитационный коллапс в астрофизике.

Демон Максвелла

Сходство энтропии Больцмана-Гиббса и энтропии Шеннона – не просто совпадение или красивая аналогия. Это одна и та же физическая величина. Конечно, физикам такое утверждение не понравится, поскольку первая величина измеряется в джоулях на кельвин, а вторая – в битах. И даже если привести эти величины к одним и тем же единицам измерения, значения у них будут различаться. Например, для микросхемы, хранящей 1 Гб данных, информационная энтропия составит порядка 10¹⁰ бит, а термодинамическая (при комнатной температуре) – порядка 10²³. Эта разница обусловлена несовпадением размера и числа степеней свободы элементарного носителя информации: энтропия Шеннона характеризует состояние кремниевого транзистора, а энтропия Больцмана – состояние атома или молекулы. Транзистор может находится в одном из двух состояний (открытом или закрытом), которым соответствуют двоичные 0 и 1 – это всего одна степень свободы. А миллиарды атомов и молекул, из которых он состоит, могут принимать самые разные значения координаты и импульса – это огромное число степеней свободы. Однако по мере миниатюризации чипов значение информационной энтропии будет приближаться к значению термодинамической энтропии материала, из которого они сделаны, в идеале – до 1 бита на атом. Таким образом, можно сказать, что шенноновская энтропия является обобщением больцмановской.

Что же связывает энергию с информацией, реальные термодинамические процессы и абстрактные вычисления? Ответ на этот вопрос кроется в разрешении парадокса, известного как демон Максвелла. Этот мысленный эксперимент был описан в 1867 г. британским физиком Джеймсом Клерком Максвеллом в работе «Об уменьшении энтропии разумными существами», где он пытался пошатнуть второй закон термодинамики и показать, что энтропия замкнутой системы может уменьшаться. Предположим, у нас есть изолированный контейнер, разделённый пополам перегородкой с небольшим закрывающимся отверстием. Контейнер равномерно заполнен нагретым газом в состоянии максимальной энтропии – теплового равновесия. Хотя в среднем температура газа будет одинаковой, отдельные молекулы всегда имеют разную энергию: одни движутся быстрее, другие – медленнее. Вводим в систему воображаемого демона, который будет регулировать затвор и пропускать в левую сторону контейнера только холодные молекулы, а в правую – только горячие. За конечное время всё тепло сосредоточится в правой стороне контейнера, и энтропия упадёт до минимума. Учёные всегда знали, что такой сценарий невозможен, но не могли объяснить, почему. И только с появлением теории информации парадокс удалось разрешить.

Предел Ландауэра

В 1929 г. Лео Силард предположил, что для оценки скоростей молекул демон Максвелла должен воспользоваться каким-нибудь измерительным прибором – например, электрическим фонариком, на работу которого будет расходоваться энергия, и вычислил минимальное количество энергии, необходимой для такого измерения. В 1953 г. Леон Бриллюэн вывел уравнение, согласно которому для записи или изменения значения информационного бита требуется энергии не менее kTln(2). Если тратить на запись бита меньше энергии, то этот бит попросту не будет читаться, независимо от его физической реализации. Из формулы следует, что температура – это, в сущности, энергия в расчёте на один бит информации: при высокой температуре на перезапись одного бита нужно больше энергии, при низкой – меньше. Когда энергия переходит в наименее доступную тепловую форму, её в принципе можно извлечь и использовать для совершения работы, но на это придётся затратить ещё больше энергии.

Как известно, в современных компьютерах архитектуры фон Неймана для записи одного бита информации используется транзистор, который кодирует 1 при наличии электрического заряда или 0 при его отсутствии. Среди элементарных логических операций (вентилей) есть обратимые (копирование, инверсия), а есть необратимые (И, ИЛИ). Копирование (запись) информации – обратимый процесс, оно может происходить без диссипации энергии и роста энтропии, при условии, что ячейка памяти изначально пустая. Но стирание информации – логически необратимый процесс, оно всегда сопровождается увеличением энтропии. Законы сохранения не допускают, чтобы энергия или информация просто исчезли. Потеря Джоуля энергии или бита информации в одном месте означает перенос такого же количества энергии и информации в другое место. В данном случае это выделение тепла. Если компьютер не будет избавляться от энтропии с помощью вентилятора, он попросту перегреется.

В 1961 г. американский физик Рольф Ландауэр в статье «Необратимость и производство тепла в процессе вычисления» сформулировал принцип, позже названный в его честь принципом Ландауэра. Суть его заключается в том, что любая логически необратимая вычислительная операция, независимо от физической реализации, увеличивает энтропию. Ни одно реальное вычисление не обходится без очистки памяти, а этот процесс сопровождается выделением тепла. Ландауэр установил для него нижний предел энтропии: W = k_B T ln2, где k_B ? постоянная Больцмана, а T ? температура вычислительной системы в кельвинах. При комнатной температуре (300 К) стирание одного бита информации производит не менее 2.7х10^-21 Дж тепловой энергии. Это очень мало. Тепловыделение современных компьютеров в тысячи раз больше, но технологии развиваются так быстро, что достижение предела Ландауэра предсказывают в течение ближайших десятилетий.

Итак, вы уже наверно догадались, как изгнать демона Максвелла. Энтропия газа в контейнере уменьшится за счёт увеличения энтропии в самом демоне. Ведь для того, чтобы сортировать молекулы, ему придётся их запоминать и где-то хранить информацию о молекулах и их движении. Второй закон термодинамики остаётся в силе, потому что энтропия газа и демона, взятых вместе, уменьшаться не может. Опираясь на работы фон Неймана и Бриллюэна, Рольф Ландауэр показал, что обнаруженный ими фундаментальный предел накладывается не на энергию, а на энтропию, создаваемую именно при стирании бита информации. Энтропия увеличивается в ходе уничтожения, а не получения информации демоном Максвелла. Последнюю точку в парадоксе демона Максвелла поставил ученик Ландауэра, физик из IBM Research Чарльз Беннетт. В 1982 г. он показал, что при конечном объёме памяти любое вычисление обязательно приведёт к необратимому уничтожению информации, поэтому хранение информации всегда физически увеличивает энтропию.

Если бы демон Максвелла был ещё и демоном Лапласа, он мог бы узнать о системе абсолютно всё, включая положение и скорость каждой молекулы, и тогда энтропия системы для него была бы равна нулю. Но специальная теория относительности Эйнштейна не позволит ему одновременно узнать состояния всех молекул, поскольку информация не может передаваться быстрее скорости света. А принцип неопределённости Гейзенберга не даст одновременно измерить координату и импульс даже одной молекулы – если точно известна одна из этих характеристик, вторая будет максимально неопределённой. В лучшем случае демон Максвелла сможет по очереди определять скорость каждой молекулы на подлёте к нему, чтобы решить, пропускать её или нет. В результате сортировки количество бит полученной им информации будет не меньше, чем количество молекул в системе. А информация – это и есть энтропия. Записывая информацию, демону Максвелла рано или поздно нужно будет её стирать, отчего он начнёт нагреваться.

Тут конечно может возникнуть искушение наделить демона бесконечной памятью, но это невозможно. Во-первых, чисто технически транзисторы для записи информации не могут быть меньше размеров атома. Использовать для этого субатомные частицы попросту неудобно, потому что они подвержены декогеренции и склонны самопроизвольно изменять свои состояния, например, квантово туннелировать. Во-вторых, есть ещё один предел, вычисленный в рамках изучения термодинамики чёрных дыр – предел Бекенштейна. Он накладывает ограничение на количество бит информации, содержащихся в заданном объёме пространства. Их не может быть больше четверти от количества планковских ячеек на поверхности этой сферы. Соответственно максимальная энтропия объекта пропорциональна не объёму, а площади его горизонта событий. Так что демон Максвелла не сможет бесконечно запоминать молекулы. Чтобы не коллапсировать в чёрную дыру, ему нужно будет или раздуваться, или всё-таки стирать информацию и каким-то образом избавляться от выделяющегося тепла.

Сколько весит информация?

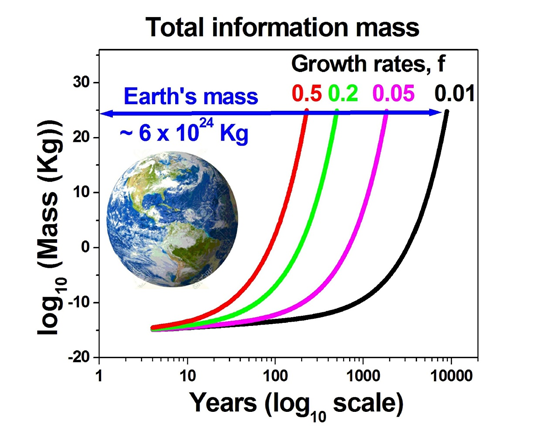
Отметим ещё один важный факт: информация обладает массой. Кому-то он покажется абсурдным, кому-то – банальным, но это прямое следствие принципа Ландауэра и эйнштейновской формулы E=mc². Поскольку масса эквивалентна энергии, а количество энергии, необходимой для обработки 1 бита информации ограничено пределом Ландауэра, можно легко вычислить массу информации. Оказывается, минимальная масса 1 бита информации составляет 3.19х10^-38 кг, что в 20 млн. раз меньше массы электрона. Например, 1 Тб данных весит всего 2.5х10^-25 кг. Обратите внимание: имеется в виду масса не носителя информации, а информации самой по себе. Эти числа показывают, сколько массы нужно преобразовать в тепловую энергию, чтобы стереть столько-то бит информации и тем самым изменить состояние носителя. Конечно, современные носители информации и весят гораздо больше, и греются сильнее. Но даже если энергоэффективность процессоров приблизится к пределу Ландауэра, скоро нам просто негде будет хранить информацию. Сейчас человечество за год производит информации массой примерно с бактерию, однако это количество удваивается раз в 5 лет. При 20-процентном годовом росте через 500 лет в цифровые данные будет преобразована половина массы Земли, а при 50-процентном росте это произойдёт уже к 2245 г. Так что нас ожидает или технологическая сингулярность, или активная космическая экспансия, или деградация и вымирание.

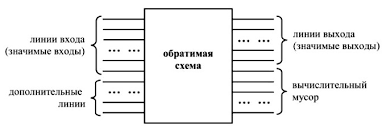
Теоретически есть возможность обойти принцип Ландауэра с помощью обратимых вычислений, в которых информация не стирается, а перемещается с места на место. В алгоритмах обратимого вычисления используются только обратимые вентили, в которых значения на входах всегда можно восстановить по значениям на выходах. Но пока неясно, смогут ли они заменить традиционные способы обработки данных. Также следует различать логическую и термодинамическую обратимость. Первую можно реализовать и на классическом компьютере, а вторая достижима только на квантовом. Впрочем, принцип Ландауэра распространяется и на квантовые компьютеры, несмотря на то, что они работают при очень низких температурах. Это экспериментально подтвердили в 2018 г. китайские учёные под руководством Миньцзы Фэна, измерив производство тепла при стирании информации в отдельном кубите. Но о квантовых демонах Максвелла и энтропии фон Неймана я расскажу в отдельной статье.

Информация в теории конструкторов

В статье «Теория конструкторов» я уже делал краткий обзор конструкторской теории информации Дойча-Марлетто. В этой теории, объединяющей классическую и квантовую теории информации, информация – не априорная математическая или логическая концепция, а вполне физическая величина, аналогичная по статусу таким величинам, как энергия или энтропия. Информация интероперабельна и независима от субстрата, т.е. сохраняет свои свойства в любой среде и при любой физической реализации. И главное – информация является контрфактической величиной: нельзя сказать, что объект в определённом физическом состоянии несёт информацию, если только он не мог бы находиться в другом состоянии.

Согласно теории конструкторов, носитель информации – это физическая система с набором атрибутов, которые можно инвертировать и копировать. Физическая система является носителем информации, если она может находится как минимум в двух состояниях и каждое из этих состояний можно скопировать. Первое свойство является универсальным, а второе относится только к информации классической, но неприменимо к информации квантовой, которую нельзя клонировать. Простейшие носители информации – это ячейка памяти, переключатель, лампочка – любой предмет, который может находится в состояниях «ВКЛ» и «ВЫКЛ» и тем самым нести один бит информации. Чтобы сигнал нёс информацию, он должен передавать одно из по крайней мере двух возможных состояний (например, точка/тире или короткий/длинный интервалы между гудками), различимых при измерении, а приёмник должен быть в состоянии передать информацию следующему получателю, сохраняя при этом свой экземпляр.

Итак, в рамках конструкторского подхода мы можем дать короткое и понятное определение информации. Классическая информация – это набор атрибутов физической системы, которые можно инвертировать и копировать. Её количество зависит от масштаба или уровня детализации, на котором проявляются эмерджентные свойства системы. Полное количество информации в системе соответствует числу её неразличимых микросостояний или степеней свободы, т.е. термодинамической энтропии Больцмана-Гиббса. Более глубокий уровень – это квантовая информация, её мы пока не касаемся. Информационную энтропию в нашем обобщении можно определить как меру взаимной различимости контрфактических (альтернативных, возможных) состояний физической системы или исходов определённого события.  Естественно, речь идёт о предельном случае, когда в сообщении нет избыточности, и важно только отличие данного сообщения от всех других возможных сообщений. Конечно, моё определение не идеально и требует дополнительных разъяснений. Как отмечают Дойч и Марлетто, «ни одна из существующих теорий информации не даёт нециклическое объяснение взаимной различимости набора физических состояний». Но здесь мы уже попадаем на поле пересечения модальной логики, теории сложности и многомировой интерпретации квантовой механики. В общем, всё как мне нравится. Надеюсь, и вам тоже.

Вывод

Итак, перечислим ещё раз основные тезисы данной статьи:

• классическая информация в широком смысле – это набор атрибутов физической системы, которые можно инвертировать и копировать;

• информация не существует без физического носителя, она дискретна и измеряется в битах;

• информация в узком смысле – это шенноновская энтропия, то есть степень неопределённости и новизны в сообщении или среднее количество информации на один символ сообщения;

• избыточность – наоборот, степень предсказуемости и упорядоченности данных;

• информационную и термодинамическую энтропии связывает предел Ландауэра – минимальное количество энергии, необходимой для стирания одного бита информации;

• информация имеет массу;

• количество информации, помещающейся в отдельно взятом объёме пространства, ограничено пределом Бекенштейна.

В следующей статье мы разберёмся, насколько информация субъективна и является ли она мерой упорядоченности системы, рассмотрим третий подход к измерению информации по Колмогорову, выясним, какие ещё существуют меры сложности, и узнаем, есть ли надёжный способ количественно измерить скрытый в информации смысл.