Правда и мифы об энтропии. Как работает второй закон термодинамики?

«Термодинамика – единственная теория, о которой я могу уверенно заявить: «Она никогда не будет низвергнута»» (Альберт Эйнштейн)

«Если кто-то скажет, что ваша любимая теория Вселенной не согласуется с уравнениями Максвелла, — тем хуже для уравнений Максвелла. Если обнаружится, что её опровергают наблюдаемые явления, — ну что тут скажешь, эти эксперимен­таторы нередко запарывают свою работу. Но если ваша теория противо­речит второму началу термодинамики, я не думаю, что у неё есть хоть какие-то шансы; ей остаётся лишь исчезнуть, потерпев унизительное по­ражение» (Артур Эддингтон)

«Доступная энергия – это главный объект, поставленный на карту в борьбе за существование и эволюцию мира» (Людвиг Больцман)

Энтропия – одна из самых важных и в то же время трудных для понимания физических концепций, без которой невозможно представить себе научную картину мира. Энтропия является неотъемлемым свойством макроскопических систем, но, в отличие от температуры, давления или объёма, её нельзя измерить с помощью приборов. Ситуацию усугубляет тот факт, что у энтропии есть множество определений, на первый взгляд никак между собой не связанных. В термодинамике это мера необратимого рассеяния или бесполезности энергии, в статистической физике – вероятность осуществления некоторого макроскопического состояния системы, в теории динамических систем – мера хаоса в поведении системы, в теории информации – мера неопределённости источника сообщений, определяемая вероятностями появления тех или иных символов при их передаче. Создаётся впечатление, что гуманитарию разобраться в этом без знания формул – непосильная задача. Но я покажу обратное. Сразу оговорюсь, что в данной статье будут рассмотрены только термодинамический и статистический аспекты энтропии, а о том, как энтропия связана с информацией, я расскажу как-нибудь отдельно.

Энтропия в термодинамике

Второй закон термодинамики нельзя рассматривать в отрыве от первого – закона сохранения энергии для термодинамических систем. Если коротко, его суть сводится к тому, что общая энергия изолированной системы всегда остаётся постоянной. Энергия не появляется из ниоткуда и никуда не исчезает, но переходит из одной формы в другую: из потенциальной в кинетическую, из химической в тепловую, из гравитационной в механическую, из ядерной в электромагнитную и т.д. Первый закон термодинамики был сформулирован Юлиусом Майером, Джеймсом Джоулем и Германом Гельмгольцем в 1840-х гг. Но в ходе экспериментов с паровыми машинами стало ясно, что не всю энергию системы можно использовать для совершения работы. Есть энергия полезная, а есть бесполезная, и последней тем больше, чем меньше разница температур между телами. Вскоре после создания бароном Кельвином абсолютной термодинамической шкалы температур (1848) в 1850 г. немецкий учёный Рудольф Клаузиус открыл второй закон термодинамики в следующей формулировке: «Теплота не может переходить сама собой от более холодного тела к более тёплому». Вроде бы очевидный и интуитивно понятный факт: стакан с горячей водой остывает, а не нагревается дальше, охлаждая комнату, и, если бросить в этот стакан кубик льда, он растает, а не охладится, нагревая воду. Пока есть разница температур, энергия пара приводит в движение поршень, а когда температура уравновешена, извлечь пользу из тепловой энергии уже невозможно. На практике это означает, что ни один двигатель не способен работать со 100-процентным КПД: какая-то часть полезной энергии будет теряться из-за трения, шума и т.д.

В 1865 г. Рудольф Клаузиус ввёл понятие энтропии (от греч. ??????? «обращение, превращение») как меры необратимого рассеивания или бесполезности энергии. В исходной трактовке энтропия была всего лишь функцией термодинамической системы, выражающей отношение количества переданного тепла к температуре. В 1876-1878 гг. американец Джозайя Гиббс вывел соответствующие уравнения и переформулировал второе начало термодинамики в закон неубывания энтропии: «в изолированной системе энтропия увеличивается или остаётся постоянной». Если замкнутая система не находится в состоянии теплового равновесия, она будет к нему стремиться, и при достижении равновесия её энтропия станет максимальной. В крайнем случае, энтропия остаётся постоянной, но только если процесс обратимый, то есть систему можно вернуть в исходное состояние без затрат энергии. Все остальные процессы, сопровождающиеся ростом энтропии, называются необратимыми.

В открытых системах энтропия ведёт себя немного иначе: она может локально уменьшатся за счёт увеличения суммарной энтропии всех взаимодействующих систем. Но есть общая тенденция: при увеличении температуры энтропия растёт. Это легко объяснимо, ведь температура – мера хаотичного движения составных частей системы, будь то свободное перемещение в пространстве молекул газа, броуновское движение молекул жидкости или колебание молекул кристаллической решётки. Следовательно, чем ниже температура, тем упорядоченнее ведут себя молекулы и тем меньше у них энтропия. Согласно третьему началу термодинамики (теореме Нернста), энтропия системы достигает минимума, когда её температура приближается к абсолютному нулю (-273°С). Минимальный уровень энтропии возможен только в кристалле из одинаковых атомов, расположенных симметрично и неподвижно. Смысл всех трёх законов термодинамики хорошо выражает теорема Гинзберга: «Ты не можешь выиграть. Ты не можешь сыграть вничью. Ты не можешь даже выйти из игры».

Энтропия в статистической механике

В термодинамике так и не было выведено общепринятого определения энтропии, что затрудняет её понимание без обращения к другим дисциплинам. Есть несколько систем термодинамической аксиоматики, и в каждой из них энтропия является базовым неопределимым понятием, наряду с температурой, теплотой и работой. Но нигде не даётся объяснения, почему энтропия предпочитает расти, а не уменьшаться. Этот недостаток был исправлен с появлением ещё одного раздела физики – статистической механики. Оказывается, энтропия изолированной системы увеличивается, потому что существует гораздо больше способов создать высокую энтропию, чем низкую.

Заслуга математического обоснования второго начала термодинамики принадлежит Людвигу Больцману, которого называют гением энтропии. В 1877 г. он установил связь энтропии с вероятностью того или иного состояния системы. Больцман рассматривал макросостояние термодинамической системы как совокупность микросостояний её отдельных молекул. В случае с газом макросостояние – это его давление, плотность, температура и другие усреднённые характеристики, а микросостояния – значения координаты и импульса каждой молекулы, количество которых в 1 моле вещества равно числу Авогадро, или порядка 10²³. Все микросостояния равновероятны, а вот вероятность получить то или иное макросостояние может сильно различаться. По формуле Больцмана, энтропия равна логарифму (степени) числа микросостояний, неразличимых с макроскопической точки зрения: S = k*log?, где S – энтропия, k – постоянная Больцмана, ? – число микросостояний. Оказалось, что макросостояние теплового равновесия статистически имеет гораздо бОльшую вероятность, чем неравновесное состояние системы с разницей температур. Физически ничто не запрещает энтропии уменьшаться, но математически вероятность этого настолько мала, что ею можно пренебречь. Самопроизвольно протекают только те процессы, в которых система из менее вероятного состояния переходит в более вероятное, а не наоборот.

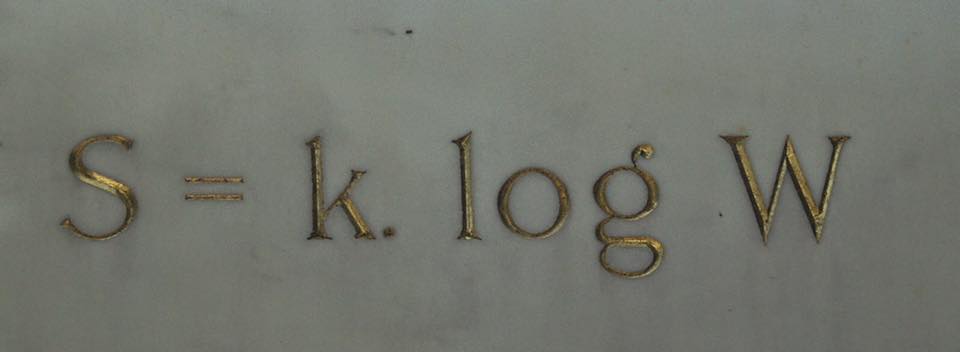
Чтобы наглядно представить энтропию по Больцману, возьмём две монеты. Назовём положение каждой из них в отдельности микросостоянием, а состояние системы в целом – макросостоянием. У одной монеты может быть два микросостояния – орёл или решка. Подбросив обе монеты, мы получим одну из четырёх равновероятных комбинаций: решка-решка, решка-орёл, орёл-решка или орёл-орёл. Но с точки зрения всей системы у нас есть всего три макросостояния: две решки, два орла и один орёл, одна решка. При этом вероятность у них получится разной: ? для двух орлов, ? для двух решек и ? для одного орла и одной решки. Третья комбинация (макросостояние) оказывается вероятней двух других, потому что её можно получить двумя разными способами (микросостояниями). Вот эта вероятность – и есть энтропия. Согласно Больцману, энтропия пропорциональна количеству микросостояний, из которых можно получить данное макросостояние. При увеличении числа микросостояний энтропия всегда будет расти. В нашем примере были только две монеты и два возможных микросостояния у каждой из них (2²=4). Если мы возьмём не две, а три монеты (2³ возможных микросостояний), вероятность выпадения трёх орлов или трёх решек составит уже 1/8, а двух решек и одного орла или двух орлов и одной решки – 3/8. С десятью монетами (2¹⁰ возможных микросостояний) получить десять орлов или десять решек будет практически нереально: вероятность такого исхода составит 1/1024. Чем больше монет, тем сильнее количество выпавших орлов и решек будет стремиться к равновесию, то есть максимальной энтропии. А если микросостояний триллионы, как молекул газа в закрытом контейнере, то не стоит рассчитывать, что они сами собой сконцентрируются в одном месте. Хотя вероятность этого не равна нулю.

Как видно из рассмотренного нами примера, энтропия по Больцману связана не столько с энергией системы, сколько с информацией о ней. Если вместо монет взять элементарные частицы, каждой из них тоже будет соответствовать одно микросостояние. Только у частиц гораздо больше степеней свободы (спин, заряд, масса, импульс, координата и т.д.), поэтому для их описания уже не хватит двух битов информации (0 или 1, орёл или решка). Рассматривая макроскопическую систему издалека, мы не можем получить всю информацию обо всех частицах, которые входят в её состав. Если система находится в жидком или газообразном состоянии, частицы внутри неё постоянно движутся. Энтропия такой системы пропорциональна числу перегруппировок частиц, не меняющих её макроскопических свойств. Если есть много способов перераспределить частицы в системе так, что при этом её внешний вид не изменится, то система имеет высокую энтропию; если таких вариантов мало, энтропия системы низкая. В случае с твёрдыми телами всё не так очевидно, потому что молекулы в их составе не перегруппируются. Как правило, молекулы твёрдого тела образуют кристаллическую решётку, по которой их положения становятся более-менее известными. Но, если система не охлаждена до абсолютного нуля, молекулы всё же совершают колебательные движения, поэтому получить всю информацию о них невозможно. Таким образом, энтропия – это мера неопределённости состояния системы. Она показывает разницу между той информацией о системе, которая нам известна (макроскопическими свойствами) и неизвестной информацией, которая скрыта в устройстве системы на микроскопическом уровне. И если вы уже потеряли какую-то часть информации о системе (например, при разрушении кристаллической структуры тающего льда), вернуть её назад будет очень сложно (придётся выслеживать траекторию каждой молекулы), поэтому у энтропии есть склонность увеличиваться.

Мифы об энтропии

Ни один другой физический закон не пытаются опровергнуть так часто, как второе начало термодинамики. Мотивы для этого у каждого свои. Кто-то хочет осчастливить человечество изобретением вечного двигателя, несмотря на то, что Парижская академия наук перестала рассматривать подобные проекты ещё в 1775 г., а в США не выдают патенты на perpetuum mobile с начала XX века. Кому-то не нравится гипотеза тепловой смерти Вселенной, хотя она уже 100 лет как устарела. Кто-то видит противоречие между законом неубывания энтропии и дарвиновской эволюцией, выдавая свою элементарную неграмотность за научную критику. А кто-то просто не понимает, что такое энтропия, и порой даже не скрывает этого, но выдумывает собственные теории и считает себя непризнанным гением. Учитывая важность темы для дальнейших статей и нездоровый интерес к ней со стороны псевдоучёных и эзотериков, мы попробуем развеять окружающие энтропию мифы.

Миф №1. Энтропия – субъективная величина, это мера незнания или количества информации о системе, неизвестной наблюдателю.

Иногда популяризаторы, стараясь упростить, говорят так: энтропия – это то, как много информации вам не известно о системе, она не является свойством объекта, а возникает из-за невозможности полного описания системы. Можно подумать, что энтропия вообще носит субъективный характер и зависит от того, кому и с какой стороны на систему смотреть. Но энтропия воды выше, чем энтропия льда, а энтропия пара выше энтропии воды, независимо от точки зрения наблюдателя. Газ выглядит как случайное распределение молекул в данном объёме, а кристалл кажется упорядоченным и сложным. Это не просто видимость: они различаются на молекулярном уровне. Можно даже определить энтропию как меру степеней свободы атомов: в кристалле у них не так много способов взаимного расположения, как в контейнере с газом. Также имеет смысл называть энтропию мерой инвариантности системы, или того, как много комбинаций составляющих её частиц будут неотличимы на макроскопическом масштабе.

Энтропию любой макроскопической системы можно вычислить по формуле Больцмана, зная приблизительное количество частиц в этой системе, или по формуле Клаузиуса, зная удельную теплоёмкость, температуру и массу. Например, если взять среднестатистического человека, его масса равна 70 кг, температура – 36,6°C или 309К, теплоёмкость – около 3000 Дж/кг*К (среднее значение между водой и льдом, что недалеко от истины, учитывая, что мы на 60-80% состоим из воды). Подставив всё это в формулу, мы выясним, что энтропия человека составляет примерно 1.2*10⁶ Дж/К. Для сравнения, энтропия Солнца по той же формуле равна 2.7*10³⁸ Дж/К, если рассматривать его как шар из водорода в агрегатном состоянии между газом и плазмой, со средней теплоёмкостью 17000 Дж/кг*К, средней температурой 8 млн. К и массой 2*10³⁰ кг. Ни много, ни мало – разница в 32 порядка.

Как и в случае с пресловутым «эффектом наблюдателя» в квантовой механике, наблюдатель не имеет к энтропии никакого отношения. Скорее энтропия зависит от масштаба, на котором рассматривается система. А ещё точнее – от количества информации, которую можно получить о системе, взаимодействуя с ней. Здесь всё сводится к абстрактному понятию системы как совокупности элементов, связанных между собой больше, чем с элементами вне этой системы. На фундаментальном уровне связи между элементарными частицами определяются квантовой запутанностью, поэтому можно сказать, что энтропия системы тем выше, чем более равномерно её элементы запутаны между собой. Подробнее о связи энтропии и квантовой запутанности речь пойдёт в следующей статье.

Миф №2. Энтропия не имеет смысла, потому что во Вселенной нет никакого беспорядка: всё строго подчинено закону причинности и происходит с определённой целью. Даже если нам кажется, что процесс беспорядочен, за этим хаосом стоит скрытый порядок.

Ещё одно распространённое упрощение, которое может ввести в заблуждение – определение энтропии как меры хаоса, или неупорядоченности системы. В обыденном понимании слова «беспорядок» и «хаос» противоположны понятию «равновесие», ведь в условиях гравитации для поддержания равновесия требуется определённым образом упорядочить предметы. Но с точки зрения термодинамики тепловое равновесие означает выравнивание температуры, и оно максимально хаотично, а неравновесное состояние системы соответствует низкой энтропии. В этом смысле низкоэнтропийное состояние действительно более упорядоченно, высокоэнтропийное – беспорядочно. При низкой энтропии движения молекул синхронизированы, при высокой – рассинхронизированы. Чем больше в поведении молекул когерентности, тем меньше в системе хаоса, и наоборот. Но здесь мы сталкиваемся с туманными выражениями вроде «скрытого порядка», «упорядоченного хаоса», «неупрощаемой сложности» и др. Частое их употребление в эзотерической и псевдонаучной литературе может сбить с толку, поэтому нужно прояснить, о чём идёт речь.

«Порядок из хаоса» – идея Ильи Пригожина, положенная им в основу неравновесной термодинамики – междисциплинарной науки, сегодня известной под названием синергетика. Ей мы посвятим отдельную статью, а пока достаточно вспомнить о предмете синергетики, чтобы понять, что она не имеет никакого отношения к данной теме. Синергетика изучает открытые диссипативные системы с нелинейной динамикой, такие как галактики, межзвёздные газопылевые облака, воздушные потоки в атмосфере, морские течения, колонии бактерий, большие популяции животных, человеческие сообщества и т.д. Поведение таких систем трудно моделировать из-за его чувствительности к начальным условиям («эффект бабочки»), но, тем не менее, оно определяется скрытым порядком (детерминированный хаос), который при определённых условиях приводит к спонтанной самоорганизации системы. А закон неубывания энтропии относится к изолированной системе, не получающей энергию извне и предоставленной самой себе. Ссылаться при описании замкнутых систем на законы синергетики – это как искать, где же в конструкции паровоза спрятана лошадь.

Другой пример нахождения скрытого порядка в окружающем хаосе – это концепция холодинамики Дэвида Бома. Её суть сводится к тому, что на первый взгляд разрозненные события могут быть нелокально связаны на другом уровне реальности, как связаны две запутанные частицы, разнесённые на многие километры. Бом предложил рассматривать видимую Вселенную как динамичную голограмму, всё прошлое, настоящее и будущее которой записаны на условной голографической пластинке с другим количеством пространственных измерений. Сегодня эта идея с некоторыми оговорками признана наукой как голографический принцип, и мы обязательно разберём её в следующих статьях. Здесь же следует отметить, что супердетерминированная Вселенная в целом вполне может быть упорядоченной и обладать нулевой энтропией, но получить полную информацию о ней не способен даже демон Лапласа. Это отнюдь не исключает увеличение энтропии отдельных её частей, которые на своём масштабном уровне кажутся несвязанными с остальной Вселенной. Так что энтропия, как и время, пространство, температура или плотность, имеет смысл по крайней мере в некоторых системах отсчёта как упрощённый способ описания более сложных процессов.

Миф №3. В соответствии с законами термодинамики, Вселенная закончит свою жизнь тепловой смертью.

Так думали первооткрыватели термодинамики в середине XIX века, сравнивая Вселенную с паровой машиной. Сегодня идея тепловой смерти безнадёжно устарела, но есть другой сценарий конца света с таким же названием, что приводит к путанице в понятиях и распространению всевозможных мифов. Автор концепции тепловой смерти Вселенной Рудольф Клаузиус понимал её как достижение теплового равновесия. Если бы Вселенная была замкнутым контейнером с газом, она бы и в самом деле стремилась к однородному распределению вещества и энергии по всему своему объёму. Но Клаузиус не принял в расчёт силу гравитации, которая стягивает вещество в сгустки и способствует высвобождению из него энергии (вспоминаем формулу E=mc²) в процессе звёздного нуклеосинтеза, тем самым увеличивая энтропию. Как показал Роджер Пенроуз, для Вселенной равномерное заполнение пространства материей соответствует низкоэнтропийному состоянию, в котором она находилась в прошлом, а высокоэнтропийное состояние наступает тогда, когда всё вещество коллапсирует в чёрные дыры.

В XIX веке также ничего не знали о расширении Вселенной, которое было открыто Эдвином Хабблом в 1929 г. Более того, в 1999 г. учёные выяснили, что Вселенная расширяется с ускорением. Причиной тому выступает загадочная тёмная энергия, которой становится тем больше, чем больше в космосе пустого пространства. Одного этого факта достаточно, чтобы понять, что закон неубывания энтропии к наблюдаемой Вселенной неприменим, ведь по отношению к тёмной энергии вакуума она является открытой системой. Почему же тогда учёные до сих пор говорят об энтропии Вселенной и её тепловой смерти?

На первый взгляд, потому что расширение должно способствовать более эффективному рассеянию вещества и увеличению его энтропии. Но вы уже знаете, что на космических масштабах энтропия растёт не при рассеянии, а при сжатии. Ускоренное расширение Вселенной как раз препятствует такому сжатию и делает возможным существование жизни и разума. По сути, расширение Вселенной – адиабатический процесс, при котором энтропия остаётся постоянной. По крайней мере, энтропия реликтового излучения почти не изменилась с момента рекомбинации 13,7 млрд. лет назад, а энтропией звёзд, планет и других объектов вообще можно пренебречь. Но суммарная энтропия Вселенной всё же растёт за счёт чёрных дыр, поэтому сценарий тепловой смерти пока никто не отменял. Просто выглядеть он будет не как медленное рассеяние вещества и уравновешивание температуры, а как поглощение вещества чёрными дырами с последующим их испарением.

Миф №4. Второе начало термодинамики и теория эволюции противоречат друг другу. Согласно закону неубывания энтропии, никакое усложнение и развитие системы невозможно, а зарождение и эволюция жизни доказывает обратное.

Этот аргумент используют как опровергатели второго начала термодинамики, так и креационисты, отрицающие дарвиновскую эволюцию. Обычно в ответ на подобные заявления достаточно сказать, что закон неубывания энтропии относится к закрытым системам, а Земля со всеми её обитателями является открытой системой, обменивающейся энергией и информацией с окружающей средой. Если где-то энтропия снижается и возникает порядок, значит, нужно искать источник свободной энергии и место, где энтропия увеличивается, притом быстрее, чем она бы делала это без очага порядка. Например, у каждого из нас дома есть холодильник. Температура воздуха внутри него ниже, чем температура воздуха в комнате, а значит, ниже и энтропия. Но в этом нет никакого чуда, потому что холодильник сбрасывает лишнюю энтропию, нагревая комнату, и увеличение энтропии комнаты будет не меньше, чем снижение энтропии холодильника. Кроме того, холодильник потребляет электроэнергию, для выработки которой на электростанциях сжигают полезные ископаемые, нагревая воздух и тоже повышая энтропию. По тому же принципу работает и кондиционер.

Жизнь не противоречит второму началу термодинамики, потому что локальное уменьшение энтропии в природе происходит за счёт увеличения энтропии в космосе. Живые организмы поддерживают своё существование, потребляя пищу и превращая её химическую энергию в тепло или кинетическую энергию тела. Основным источником энергии для нашей планеты является Солнце, сжигающее около 4 млн тонн водорода в секунду. Земля частично отражает солнечный свет, а частично поглощает и отдаёт назад уже в виде тепла, чему во многом способствует биосфера. Если бы она этого не делала, температура земной поверхности довольно быстро сравнялась бы с температурой поверхности Солнца (5800 К). На каждый высокоэнергетичный фотон солнечного света, поглощаемый Землёй, приходится 20 низкоэнергетичных фотонов инфракрасного излучения, возвращаемых ею в космос. Таким образом, живые организмы служат катализаторами в процессе увеличения энтропии Вселенной, хотя это увеличение и ничтожно в сравнении с другими космическими процессами.

Вообще тенденция к увеличению энтропии не исключает возрастания сложности. Более того, сложность как раз и возникает благодаря второму закону термодинамики. Чтобы понять, как это происходит, нужно разобраться с самими терминами «сложность», «порядок», «неупорядоченность» и «хаос». Интуитивно мы ассоциируем сложность с низкой энтропией, а простоту – с высокой. Действительно, упорядоченная мозаика кажется сложнее кучи перемешанных цветных камешков, а целое яйцо – сложнее омлета. С точки зрения статистической механики, информатики и квантовой физики всё наоборот: неупорядоченная система сложнее упорядоченной, потому что для её описания нужно больше данных. Частицы газа содержат больше квантовой информации, чем атомы кристалла. Какой же из этих подходов правильнее? Ни тот, ни другой. Эффективная сложность макроскопической системы не равна её упорядоченности, но и не связана с количеством квантовой информации в системе. Эволюция сложности коррелирует с динамикой роста энтропии, но не совпадает с ней. На графике это выглядит так:

С течением времени энтропия всегда растёт, а сложность растёт вместе с ней только вначале, затем достигает вершины в середине процесса и начинает убывать, пока не упадёт до нуля при максимальной энтропии. В качестве примера можно привести смешивание кофе со сливками в прозрачном стакане. Если аккуратно налить сливки поверх кофе, мы получим довольно простую систему из двух отдельных жидкостей разного цвета. Энтропия у такой системы низкая, сложность – тоже. Чтобы ускорить процесс и внести в него элемент случайности, начнём хаотично перемешивать ложкой содержимое стакана. Взаимодействуя, кофе и сливки образуют красивый узор из белых и коричневых завитков. Энтропия системы увеличилась, сложность стала максимальной. А дальше система начинает упрощаться: контрастные цвета смешиваются в однородную коричневую жидкость. Энтропия достигает максимума, сложность падает до минимума. Обратите внимание: сложность при увеличении энтропии возникает не всегда, а только при определённых условиях. На начальном этапе система чувствительна к слабым возмущениям, и, если они присутствуют, запускается цепочка положительной обратной связи, которая приводит к самоорганизации и формированию фрактальных (масштабно самоподобных) структур.

Аналогичные процессы происходят во Вселенной. Она развивается из однородного состояния с низкой энтропией (Большой взрыв) в однородное состояние с высокой энтропией (тепловая смерть или Большой разрыв), а все неоднородности и сложные структуры возникают на промежуточном этапе. Нынешняя Вселенная со всеми галактиками, звёздами и планетами гораздо сложнее горячей протон-нейтронной плазмы в первые минуты её существования или ожидающего её в конце холодного пустого пространства с редкими следами низкоэнергетичных частиц. Но всей своей сложностью она обязана второму началу термодинамики, заставляющему энергию переходить из более упорядоченной в менее упорядоченную форму. Пожалуй, это одно из самых парадоксальных и контринтуитивных свойств нашего мира. Хотя, если понимать механизм самоорганизации, возникновение сложных систем вроде бактерий, растений, животных и людей из первичных квантовых флуктуаций вакуума покажется уже не таким удивительным.

Миф №5. Вечный двигатель возможен.

Если это так, почему же мы его до сих пор не используем? История физики знает множество забавных конструкций, в своё время претендовавших на роль вечного двигателя, но ни одна из них так и не заработала. В наши дни по-настоящему эффективные изобретения трудно утаить или затормозить их развитие, как показывает ситуация с генеративными языковыми моделями. Конечно, конспирологи скажут, что вечный двигатель уже много раз изобретали, но из-за сговора учёных, мирового правительства и нефтяных корпораций мы вынуждены до сих пор платить за бензин, газ и электричество. Возражать против этого бессмысленно, если вы не хотите, чтобы вас причислили к участникам заговора. Поэтому отсутствие вечных двигателей на практике – не аргумент. А что запрещает создать perpetuum mobile в теории? Если вы внимательно читали эту статью, то могли заметить, что энтропия нарастает чисто статистически, но ни один закон физики не запрещает ей уменьшаться. Так может, для создания вечного двигателя достаточно научиться выбирать тот маловероятный сценарий, по которому энергия не рассеивается?

Вечный двигатель — это машина, которая производит энергию для поддержания собственной работы. Вы наверняка видели все эти колёса Бхаскары с шарнирами, переливающимися жидкостями или перекатывающимися шариками, архимедовы цепи самовыталкивающихся поплавков, самовращающиеся мельницы, самонаполняющиеся сосуды, магнитные рампы, самоходные часы, бестопливные генераторы на постоянных магнитах и т.д. Почему все эти конструкции не работают, догадаться нетрудно, а для тех, кто сам не понимает, есть подробные разоблачения в интернете. В лучшем случае удаётся построить т.н. псевдовечный двигатель, у которого есть внешний источник энергии, но он неочевиден – например, часы Кокса. Также существуют устройства, которые якобы извлекают энергию вакуума или эфира, но они не подпадают под определение вечного двигателя и выходят за рамки данной статьи.

Вечные двигатели делят на два или три рода в зависимости от того, какой закон термодинамики они нарушают. Но в большинстве случаев эти машины нарушают и первый, и второй законы, так что классификация весьма условная.

Вечный двигатель первого рода нарушает закон сохранения энергии. Такой мотор мог бы совершать работу без затрат энергии и без потребления топлива, или производить больше энергии, чем поглощать, то есть иметь КПД более 100% и выступать источником бесплатной самовозобновляемой энергии. Почему энергия не берётся из ниоткуда? Согласно теореме Нётер, закон сохранения энергии является следствием однородности времени, то есть независимости законов физики от момента времени, в который рассматривается система. Если вы не сомневаетесь в фундаментальных симметриях и в том, что законы физики не меняются со временем, то вам придётся отказаться от идеи вечного двигателя первого рода.

Связь между математическими симметриями и законами сохранения – это основа современной физики. Как пишет Майкл Данос в статье о теореме Нётер в квантовой теории поля (1997), «… любые результаты, которые, кажется, нарушают эту теорему, могут быть немедленно объявлены скрытой ошибкой в вычислениях». А свидетельством неизменности физических законов и постоянства фундаментальных констант является сама наблюдаемая Вселенная. Мы можем изучать её с помощью телескопов такой, какой она была миллиарды лет назад, проводить спектральный анализ и сравнивать звёзды в самых древних галактиках с современными, расположенными в пределах Млечного пути. Кроме того, вечный двигатель первого рода является примером бесконечной автореференции или рекурсии, он логически противоречит сам себе, подобно компьютеру, вычисляющему собственное поведение в будущем или решающему проблему остановки. Таким образом, вечный двигатель первого рода невозможен не только в нашей Вселенной с её законами физики, но и во всех математически и логически возможных мирах.

Вечный двигатель второго рода нарушает второй закон термодинамики, преобразуя тепловую энергию в механическую работу. В формулировке Вильгельма Оствальда (1892 г.) второй закон прямо говорит о невозможности создания вечного двигателя второго рода, то есть циклически действующей изотермической тепловой машины, способной работать от одного теплового резервуара и, следовательно, преобразовывать в работу всю энергию, извлекаемую из имеющей постоянную температуру окружающей среды. Для работы такого двигателя всё же необходима энергия, но он использует её всю без остатка, без перевода кинетической энергии через трение в теплоту, и не оставляет никаких изменений в окружающих телах. К вечным двигателям второго рода относятся воображаемые машины вроде демона Максвелла или броуновского храповика, якобы способные извлекать энергию из хаотичного движения молекул путём их сортировки. Объяснить, почему они не работают, учёные смогли только в 60-е гг. XX века с развитием информатики, в частности с помощью принципа Ландауэра.

Ещё выделяют вечный двигатель третьего рода, поддерживающий движение за счёт инерции массы при полном устранении трения и других диссипативных процессов. Казалось бы, планеты, звёзды и другие космические тела могут двигаться в пространстве вечно, но на самом деле даже они незначительно замедляются из-за трения в межзвёздном газе и рассеяния энергии в виде гравитационных волн. А о вечном движении в воздухе, при комнатной температуре и атмосферном давлении и речи не может быть.

Вечный двигатель возможен лишь при условии, что он является замкнутой системой с постоянной нулевой энтропией. Тогда его работа будет полностью обратимым процессом, то есть таким процессом, который может проходить в обратном направлении через те же промежуточные стадии и возвращать систему в исходное состояние без затрат энергии. Мы же знаем из практики, что все реальные процессы необратимы, потому что проходят только вперёд во времени и производят энтропию. Впрочем, эта необратимость может быть только кажущейся. Если проследить движение частиц рассеивающегося газа в замкнутом контейнере на микроскопическом масштабе, оно будет одинаковым как вперёд, так и назад во времени. Взятые по отдельности, молекулы с равной вероятностью могут оказаться в любой точке контейнера, и им ничто не запрещает собраться в одном углу. Но в совокупности они так никогда себя не ведут, потому что вероятность счастливого совпадения их координат крайне мала.

И всё-таки квантовая механика оставляет небольшую лазейку, позволяющую обмануть энтропию, не нарушая второго закона термодинамики. Для этого нужно полностью исключить трение и шум, поместить двигатель в вакуум и охладить почти до абсолютного нуля. Так можно получить сверхтекучую жидкость, достичь сверхпроводимости или создать квантовый компьютер. В некоторых случаях работу квантового компьютера можно ненадолго повернуть вспять, снизив энтропию до минимума. Или приготовить особое состояние вещества – темпоральный кристалл, совершающий движение без затрат энергии. В каком-то смысле такой кристалл является вечным двигателем, вот только извлечь из него энергию не получится. Подробнее мы рассмотрим эти эксперименты в следующей статье.

Энтропия растёт

Ну и конечно же я не могу не написать пару слов о частных проявлениях энтропии в нашей жизни, на которые обращают внимание думеры и нигилисты. Даже если вы не относитесь к этим категориям населения, вам наверняка приходилось слышать выражения типа «энтропия растёт», «жизнь – тлен», «ни в чём нет смысла», «никогда не бывает так плохо, чтобы не могло стать ещё хуже» и т.д. Кажется, такой взгляд на вещи вполне оправдан вторым началом термодинамики, которое называют самым трагическим законом физики. Действительно, мир неуклонно движется к беспорядку. Беспорядок наступает сам собой, а для поддержания порядка необходимо прилагать усилия. С этим тесно связан закон Мёрфи («Если что-нибудь может пойти не так, оно пойдёт не так») и все его следствия. Бороться с энтропией бесполезно – рано или поздно мы все умрём, потому что есть гораздо больше способов быть мёртвым, чем живым. Вот Людвиг Больцман якобы всё это понял и повесился в гостиничном номере на шнурке от штор. А может, он покончил с собой из-за того, что его самого никто не понял в научных кругах. Некоторые лентяи приходят к выводу, что лучшая стратегия – ничего не делать, потому что так мы будем производить меньше энтропии и отсрочим тепловую смерть Вселенной.

На самом же деле в масштабах космоса ваш вклад в повышение энтропии едва ли будет различим, но в масштабах цивилизации вы можете привнести много порядка. Ничто не мешает нам локально создавать порядок, даже если это увеличит энтропию Вселенной в целом. А основа всякого порядка – знание, которое помогает решать любые проблемы. Поэтому, если вы не знаете, как справиться с проблемами и как упорядочить свою жизнь, лучшее, с чего вы можете начать – получать новые знания. В дальнейшем я продемонстрирую, что второй закон термодинамики даёт больше поводов для оптимизма, чем для пессимизма, и не только в виде радости, что мы живём в такое время, когда энтропия ещё может расти и расти, до максимума ей очень далеко.

Вывод

Вместо заключения повторим ещё раз самые важные моменты. Термодинамика – это по сути система постулатов, которая пока не имеет опоры в законах фундаментальной физики, но подтверждается на практике. Главные две аксиомы – закон сохранения энергии и закон неубывания энтропии – относятся преимущественно к изолированным системам наподобие герметичного контейнера с газом. В таких системах наблюдается рост энтропии: полезная энергия переходит в тепло, а температура уравновешивается. Энтропию можно понимать в трёх аспектах: как меру бесполезности энергии, как меру неупорядоченности системы и как меру неопределённости её состояния. Первый аспект изучает термодинамика, второй – статистическая механика, третий – теория информации.

В следующих статьях я буду неоднократно показывать, как работает закон неубывания энтропии на разных масштабах и в различных физических процессах: от квантовой декогеренции до эволюции звёзд, от формирования крупномасштабной структуры Вселенной до компьютерных вычислений, от зарождения жизни до испарения чёрных дыр. Охватив всю научную картину мира, вы убедитесь, что второй закон термодинамики лежит в основе универсальной эволюции и управляет любым процессом обработки информации, включая наше мышление. Впереди вас ждёт знакомство с квантовой энтропией фон Неймана, информационной энтропией Шеннона и энтропией чёрных дыр Бекенштейна-Хокинга. Также мы выясним, есть ли физическая величина, противоположная энтропии, и как можно её измерить.