From Theory to Practice: Building a k-Nearest Neighbors Classifier

От теории к практике: построение классификатора k-ближайших соседей

Классификатор k-ближайших соседей — это алгоритм машинного обучения, который присваивает новую точку данных наиболее распространенному классу среди k ближайших соседей. В этом руководстве вы изучите основные этапы создания и применения этого классификатора в Python.

Доктор Роберт Каблер, старший научный сотрудник, 27 июня 2023 г., машинное обучение

Еще один день, еще один классический алгоритм: k ближайших соседей. Как и наивный байесовский классификатор, это довольно простой метод решения задач классификации. Алгоритм интуитивно понятен и имеет непревзойденное время обучения, что делает его отличным кандидатом для изучения, когда вы только начинаете свою карьеру в машинном обучении. Сказав это, делать прогнозы мучительно медленно, особенно для больших наборов данных. Производительность для наборов данных со многими функциями также может быть не слишком высокой из-за проклятия размерности.

В этой статье вы узнаете

     как работает классификатор k-ближайших соседей
     почему это было спроектировано так
     почему у него такие серьезные недостатки и, конечно же,
     как реализовать это на Python с помощью NumPy.

Поскольку мы будем реализовывать классификатор в стиле scikit-learn, также стоит ознакомиться с моей статьей Создайте свою собственную регрессию scikit-learn. Тем не менее, накладные расходы scikit-learn довольно малы, и вы все равно сможете следовать им.

     Вы можете найти код на моем Github.

Теория

Основная идея этого классификатора потрясающе проста. Это непосредственно вытекает из фундаментального вопроса о классификации:

     Учитывая точку данных x, какова вероятность того, что x принадлежит некоторому классу c?

На языке математики мы ищем условную вероятность p(c|x). В то время как наивный байесовский классификатор пытается смоделировать эту вероятность напрямую, используя некоторые предположения, существует еще один интуитивный способ вычисления этой вероятности — частотный взгляд на вероятность.

Наивный взгляд на вероятности

Хорошо, но что это значит сейчас? Давайте рассмотрим следующий простой пример: вы бросаете шестигранную, возможно, подтасованную игральную кость и хотите вычислить вероятность того, что выпадет шестерка, т. е. p (выпало число 6). Как это сделать? Итак, вы бросаете кубик n раз и записываете, как часто выпадала шестерка. Если вы видели число шесть k раз, вы говорите, что вероятность увидеть шестерку составляет около k/n. Здесь нет ничего нового или необычного, верно?

Теперь представьте, что мы хотим вычислить условную вероятность, например

     p(бросок номер 6 | бросок четного числа)

Вам не нужна теорема Байеса, чтобы решить это. Просто бросьте кубик еще раз и игнорируйте все броски с нечетным числом. Вот что делает обусловливание: фильтрует результаты. Если вы бросили кубик n раз, увидели m четных чисел и k из них были шестерками, указанная выше вероятность составляет около k/m вместо k/n.

Мотивация k-ближайших соседей

Вернемся к нашей проблеме. Мы хотим вычислить p(c|x), где x — вектор, содержащий функции, а c — некоторый класс. Как и в примере с кубиком, мы

     нужно много точек данных,
     отфильтровать те, у которых есть функции x и
     проверьте, как часто эти точки данных принадлежат классу c.

Относительная частота — это наше предположение о вероятности p(c|x).

     Вы видите здесь проблему?

Обычно у нас не так много точек данных с одинаковыми функциями. Часто только один, может два. Например, представьте набор данных с двумя характеристиками: рост (в см) и вес (в кг) людей. Этикетки бывают мужские или женские. Таким образом, x=(x?, x?), где x? это высота и х? — вес, а c может принимать значения мужского и женского пола. Давайте посмотрим на некоторые фиктивные данные:

Поскольку эти две характеристики непрерывны, вероятность наличия двух точек данных, не говоря уже о нескольких сотнях, ничтожно мала.

Еще одна проблема: что произойдет, если мы захотим предсказать пол для точки данных с функциями, которые мы никогда раньше не видели, такими как (190,1, 85,2)? Это то, что предсказание на самом деле все о. Вот почему этот наивный подход не работает. Вместо этого алгоритм k-ближайшего соседа делает следующее:

     Он пытается аппроксимировать вероятность p(c|x) не точками данных, которые имеют точно такие же признаки x, а точками данных с признаками, близкими к x.

В каком-то смысле он менее строг. Вместо того, чтобы ждать множество людей с ростом = 182,4 и весом = 92,6 и проверять их пол, k-ближайших соседей позволяет рассматривать людей, близких к обладающим этими характеристиками. k в алгоритме — это количество людей, которых мы рассматриваем, это гиперпараметр.

     Это параметры, которые должны выбрать мы или алгоритм оптимизации гиперпараметров, такой как поиск по сетке. Они напрямую не оптимизируются алгоритмом обучения.

От теории к практике: построение классификатора k-ближайших соседейОт теории к практике: построение классификатора k-ближайших соседей
Изображение автора.

Алгоритм

Теперь у нас есть все необходимое для описания алгоритма.

Обучение:

     Организуйте обучающие данные каким-либо образом. Во время прогнозирования этот порядок должен позволить нам получить k ближайших точек для любой заданной точки данных x.
     Это уже! ?

Прогноз:

     Для новой точки данных x найдите k ближайших соседей в организованных обучающих данных.
     Совокупность меток этих k соседей.
     Выведите метку/вероятности.

Мы пока не можем это реализовать, потому что есть много пробелов, которые нам нужно заполнить.

     Что значит организовать?
     Как мы измеряем близость?
     Как суммировать?

Помимо значения k, это все, что мы можем выбрать, и разные решения дают нам разные алгоритмы. Давайте упростим задачу и ответим на вопросы следующим образом:

     Организация = просто сохраните набор обучающих данных как есть
     Близость = евклидово расстояние
     Агрегация = усреднение

Это требует примера. Давайте еще раз проверим картинку с данными человека.
От теории к практике: построение классификатора k-ближайших соседейОт теории к практике: построение классификатора k-ближайших соседей

Мы видим, что k = 5 ближайших к черному точек данных имеют 4 мужских метки и одну женскую метку. Таким образом, мы могли бы вывести, что человек, принадлежащий к черной точке, на самом деле на 4/5=80% мужчина и на 1/5=20% женщина. Если бы мы предпочли один класс в качестве вывода, мы бы вернули male. Без проблем!

Теперь давайте реализуем это.

Выполнение

Самое сложное — найти ближайших соседей к точке.

Быстрый учебник

Давайте сделаем небольшой пример того, как вы можете сделать это в Python. Мы начинаем с

import numpy as np    features = np.array([[1, 2], [3, 4], [1, 3], [0, 2]])  labels = np.array([0, 0, 1, 1])    new_point = np.array([1, 4])

Image by the Author.

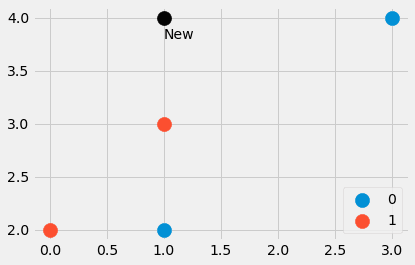
Изображение автора.

Мы создали небольшой набор данных, состоящий из четырех точек данных, а также еще одной точки. Какие ближайшие точки? И должна ли новая точка иметь метку 0 или 1? Давайте узнаем. Ввод

расстояния = ((функции - новая_точка)**2).сумма(ось=1)

дает нам четыре значения расстояний = [4, 4, 1, 5], которые представляют собой квадрат евклидова расстояния от new_point до всех других точек в объектах. Сладкий! Мы видим, что точка номер три является ближайшей, за ней следуют точки номер один и два. Четвертая точка самая дальняя.

Как теперь извлечь ближайшие точки из массива [4, 4, 1, 5]? Distances.argsort() помогает. Результатом является [2, 0, 1, 3], что говорит нам о том, что точка данных с индексом 2 является наименьшей (выходная точка номер три), затем точка с индексом 0, затем с индексом 1 и, наконец, точка с индексом 3 самый большой.

Обратите внимание, что argsort помещает первые 4 расстояния перед вторыми 4. В зависимости от алгоритма сортировки это может быть и наоборот, но давайте не будем вдаваться в эти подробности в этой вводной статье.

Как, например, если нам нужны три ближайших соседа, мы могли бы получить их через

расстояния.argsort()[:3]

а метки соответствуют этим ближайшим точкам через

метки[расстояния.argsort()[:3]]

Получаем [1, 0, 0], где 1 — метка ближайшей к (1, 4) точки, а нули — метки, принадлежащие двум следующим ближайшим точкам.

Это все, что нам нужно, давайте перейдем к делу.

Окончательный код

Вы должны быть хорошо знакомы с кодом. Единственная новая функция — np.bincount, которая подсчитывает вхождения меток. Обратите внимание, что сначала я применил метод predict_proba для вычисления вероятностей. Метод predict просто вызывает этот метод и возвращает индекс (=класс) с наибольшей вероятностью, используя функцию argmax. В классе ожидаются классы от 0 до С-1, где С — количество классов.

Отказ от ответственности: этот код не оптимизирован, он служит только для образовательных целей.

from sklearn.datasets import make_blobs  import numpy as np    X, y = make_blobs(n_samples=20, centers=[(0,0), (5,5), (-5, 5)], random_state=0)  X = np.vstack([X, np.array([[2, 4], [-1, 4], [1, 6]])])  y = np.append(y, [2, 1, 0])

It looks like this:

Using our classifier with k = 3

my_knn = KNNClassifier(k=3)  my_knn.fit(X, y)    my_knn.predict_proba([[0, 1], [0, 5], [3, 4]])

we get

array([[1.        , 0.        , 0.        ],         [0.33333333, 0.33333333, 0.33333333],         [0.        , 0.66666667, 0.33333333]])

Прочитайте вывод следующим образом: первая точка на 100% принадлежит к классу 1, вторая точка принадлежит к каждому классу поровну по 33%, а третья точка примерно на 67% относится к классу 2 и на 33% к классу 3.

Если вам нужны конкретные этикетки, попробуйте

my_knn.predict([[0, 1], [0, 5], [3, 4]])

который выводит [0, 0, 1]. Обратите внимание, что в случае ничьей модель в том виде, в каком мы ее реализовали, выдает более низкий класс, поэтому точка (0, 5) классифицируется как принадлежащая классу 0.

Если вы посмотрите на картинку, это имеет смысл. Но давайте успокоим себя с помощью scikit-learn.

from sklearn.neighbors import KNeighborsClassifier    knn = KNeighborsClassifier(n_neighbors=3)  knn.fit(X, y)    my_knn.predict_proba([[0, 1], [0, 5], [3, 4]])

The result:

array([[1.        , 0.        , 0.        ],         [0.33333333, 0.33333333, 0.33333333],         [0.        , 0.66666667, 0.33333333]])

Фу! Все выглядит хорошо. Давайте проверим границы решений алгоритма, просто потому, что это красиво.

Опять же, верхняя черная точка не на 100% синяя. Это 33% синего, красного и желтого, но алгоритм детерминистически выбирает самый низкий класс, то есть синий.

Мы также можем проверить границы решений для разных значений k.

Обратите внимание, что синяя область в конце становится больше из-за предпочтительного отношения к этому классу. Мы также можем видеть, что для k=1 границы беспорядочны: модель переоснащается. На другой стороне экстремума k равно размеру набора данных, и все точки используются для шага агрегирования. Таким образом, каждая точка данных получает один и тот же прогноз: класс большинства. В данном случае модель не подходит. Золотая середина находится где-то посередине и может быть найдена с помощью методов оптимизации гиперпараметров.

Прежде чем мы дойдем до конца, давайте посмотрим, какие проблемы есть у этого алгоритма.

Недостатки k-ближайших соседей

Проблемы заключаются в следующем:

     Поиск ближайших соседей занимает много времени, особенно с нашей наивной реализацией. Если мы хотим предсказать класс новой точки данных, мы должны сравнить ее с каждой другой точкой в нашем наборе данных, что является медленным. Есть лучшие способы организации данных с использованием расширенных структур данных, но проблема остается.
     Следующая проблема № 1: обычно вы обучаете модели на более быстрых и сильных компьютерах, а затем можете развернуть модель на более слабых машинах. Подумайте, например, о глубоком обучении. Но для k-ближайших соседей время обучения простое, а тяжелая работа выполняется во время прогнозирования, а это не то, что нам нужно.
     Что произойдет, если ближайшие соседи совсем не рядом? Тогда они ничего не значат. Это уже может произойти в наборах данных с небольшим количеством признаков, но с еще большим количеством признаков вероятность столкнуться с этой проблемой резко возрастает. Это также то, что люди называют проклятием размерности. Хорошую визуализацию можно найти в этом посте Кэсси Козырков.

От теории к практике: построение классификатора k-ближайших соседейОт теории к практике: построение классификатора k-ближайших соседей

Особенно из-за проблемы 2 вы не слишком часто видите классификатор k-ближайших соседей в дикой природе. Это все еще хороший алгоритм, который вы должны знать, и вы также можете использовать его для небольших наборов данных, в этом нет ничего плохого. Но если у вас есть миллионы точек данных с тысячами функций, все становится тяжело.

Заключение

В этой статье мы обсудили, как работает классификатор k-ближайших соседей и почему его конструкция имеет смысл. Он пытается оценить вероятность того, что точка данных x принадлежит классу c, насколько это возможно, используя точки данных, наиболее близкие к x. Это очень естественный подход, и поэтому этот алгоритм обычно преподается в начале курсов по машинному обучению.

     Обратите внимание, что также очень просто построить регрессор k-ближайших соседей. Вместо подсчета вхождений классов просто усредните метки ближайших соседей, чтобы получить прогноз. Вы можете реализовать это самостоятельно, это всего лишь небольшое изменение!

Затем мы реализовали его простым способом, имитируя API scikit-learn. Это означает, что вы также можете использовать этот оценщик в конвейерах scikit-learn и поиске по сетке. Это большое преимущество, поскольку у нас даже есть гиперпараметр k, который можно оптимизировать с помощью поиска по сетке, случайного поиска или байесовской оптимизации.

Однако этот алгоритм имеет ряд серьезных недостатков. Он не подходит для больших наборов данных и не может быть развернут на более слабых машинах для прогнозирования. Вместе с подверженностью проклятию размерности этот алгоритм теоретически хорош, но его можно использовать только для небольших наборов данных.

     Доктор Роберт Каблер — специалист по данным в METRO.digital и автор книги «На пути к науке о данных».

   Оригинал. Перепечатано с разрешения.

Подробнее по этой теме

     Ближайшие соседи для классификации
     K-ближайшие соседи в Scikit-learn
     Как создать классификатор изображений в нескольких строках кода с помощью Flash
     Как обучить классификатор извлечения совместных сущностей и отношений с помощью BERT…
     Что такое теория графов и почему вас это должно волновать?
     Первые принципы теории обобщения