Уделываем классические компьютеры при помощи Borealis

Эта история повествует о первом в мире общедоступном квантовом компьютере, развёрнутом в облаке.

Компания Xanadu весной 2022 года объявила о запуске Borealis, новейшего квантового компьютера, развёрнутого в облаке и предоставленного в общий доступ. В этом компьютере 216 кубитов в сжатом состоянии – то есть, почти в 20 раз больше, чем в X12, системе предыдущего поколения, также действовавшей в облаке. Borealis – это крупнейший в истории фотонный квантовый компьютер, а также первая в своём роде машина, предоставленная в публичное использование.
Ещё примечательнее сама та мощь, которую Borealis обеспечивает при решении очень специфичной математической задачи, именуемой «Гауссов бозонный сэмплинг». Говоря абстрактно, эта задача касается генерации случайных чисел, и эти числа подчиняются определённым паттернам, выражаемым математической функцией под названием «гафниан». Подробности данной конкретной математической задачи в рамках этой статьи не очень важны. Суть в том, что этот пример отлично позволяет продемонстрировать, насколько классические компьютеры уступают по мощности квантовым. Оказывается, что вычислить такую функцию на классическом компьютере поразительно тяжело. На самом деле, генерация случайных образцов со свойствами, описываемыми гафнианом, для классических машин становится попросту неподъёмной, стоит только размеру ввода превысить некоторый предел. Borealis был спроектирован именно для того, чтобы дотянуться до пространства таких математических задач. На Borealis пользователи могут запускать собственные программы для кодирования матриц, а машина будет возвращать пользователю вычисленный вывод. Вывод в данном случае – это образцы из вероятностного распределения, основанного на заданном пользователем гафниане.

Чтобы продемонстрировать возможности Borealis во всей красе, мы подвергли его одному из самых требовательных тестов в области квантовых вычислений: заставили показать вычислительное квантовое преимущество. Иногда в данном случае также говорят о достижении квантового превосходства. То есть, требуется показать, что при решении конкретной чётко очерченной задачи рассматриваемый квантовый компьютер обставляет самые быстрые из существующих классических компьютеров, даже если те используют для решения задачи наилучшие известные алгоритмы. Исключительно сложно собрать такую квантовую машину, которая преодолеет этот рубеж, поэтому известно всего несколько случаев, в которых удалось достичь квантового вычислительного преимущества. Впервые это сделала команда инженеров из Google в 2019, воспользовавшись собственным 53-кубитным сверхпроводящим процессором Sycamore и выполнив на нём немного иной алгоритм случайной выборки. Вскоре после этого гауссов бозонный сэмплинг был продемонстрирован на оптическом компьютере Цзючжан, который собрала команда инженеров из Научно-технического университета Китая. Затем та же группа продемонстрировала собственный сверхпроводящий процессор, а также усовершенствовала Цзючжан, чтобы показать более зрелищный оптический опыт. На момент написания этой статьи ни одна другая машина – ни из академических исследовательских групп, ни из коммерческих компаний – не позволила достичь квантового вычислительного преимущества.

Но Borealis, представьте себе, прорвался через этот барьер, с честью пройдя тест и стал первым компьютером, демонстрирующим квантовое превосходство и потенциально подходящим для развёртывания в облаке. Во время выполнения он показывает чрезвычайное преимущество над классическими компьютерами. Самому мощному современному суперкомпьютеру потребовалось бы приблизительно 9000 лет, чтобы дать единственный результат, при условии, что задача будет решаться методом прямой симуляции. Borealis на то же требуется всего 36 микросекунд. Это беспрецедентный выигрыш по сравнению с тем, что дают оптические машины. Он более чем в 50 миллионов раз превышает то квантовое преимущество, которое было показано на более ранних фотонных квантовых машинах. Результаты теста прошли экспертную оценку и были представлены в статье, опубликованной в научном журнале Nature. Вот как можно писать код для Borealis на Python и Strawberry Fields от Xanadu. Чтобы запрограммировать ваши собственные задачи и выполнить их на Borealis, требуется всего лишь зайти под логином на соответствующий облачный сервис и загрузить туда свои задания. Borealis не только первым из себе подобных развёрнут в облаке, но претендует и ещё на ряд других важных первенств. Наиболее принципиально, что это первый фотонный квантовый компьютер, демонстрирующий квантовое превосходство и при этом обеспечивающий полную программируемость всех своих вентилей. Пользователь, пишущий программу, волен задавать более 1200 параметров, а также указывать яркость входных кубитов, находящихся в сжатом состоянии. Да, сверхпроводящий компьютер Sycamore можно было программировать, но в более ранних фотонных машинах явно не доставало такого обширного контроля. Работа с ними была в основном ограничена операциями над фиксированными рандомизированными последовательностями вентилей.

Borealis родился в лабораториях Xanadu в Торонто, откуда (с верхнего этажа офисной башни) открывается вид на деловой центр города. Так как же работает Borealis, для чего его можно использовать, и какова технологическая подоплёка этого достижения с точки зрения разработки практически полезных квантовых компьютеров?

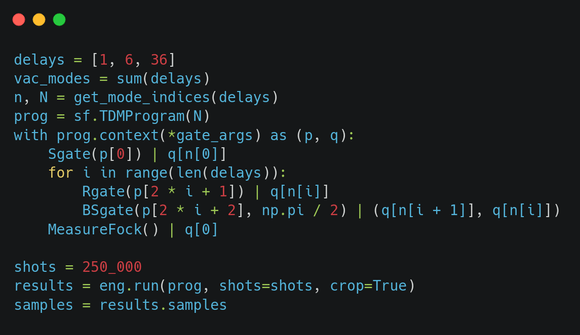
? Заглянем под капот: как работает Borealis

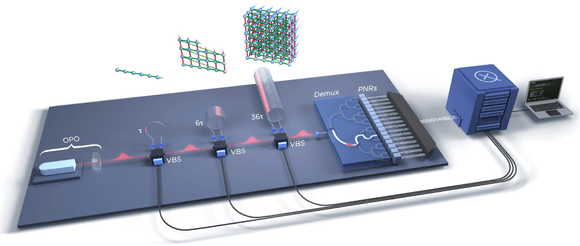
Borealis обладает уникальной архитектурой, спроектированной для генерации и обработки большого количества кубитов, находящихся в сжатом состоянии, причём, с эффективной аппаратной поддержкой. Для того, чтобы сгенерировать и запутать нужное нам состояние, используется мультиплексирование времени, где источник кубитов в сжатом состоянии производит вереницу из 216 импульсов сжатого света. Каждый такой импульс состоит из пары фотонов, находящихся в квантовой суперпозиции. Фотоны генерируются пропусканием ярких лазерных вспышек сквозь нелинейный кристалл, расположенный в оптическом резонаторе. На следующей схеме в общем виде представлено устройство всей машины, чтобы было проще понять, какую роль играет каждая подсистема:

В Borealis кубиты, находящиеся в сжатом состоянии, генерируются в нелинейном кристалле, расположенном в оптическом резонаторе. Этот резонатор называется «оптический параметрический осциллятор» (ОПО). После этого кубиты направляются на расположенные в ряд три циклических интерферометра. На показанной выше схеме можно визуализировать над каждым циклом запутанность соответствующих компонентов. В итоге получаем трёхмерное запутанное состояние. Такая запутанность контролируется светоделителями с регулируемым коэффициентом (VBS) и оптоволоконными линиями задержки. Считывание данных осуществляется при помощи демультиплексора (разуплотнителя), за которым следует решётка из детекторов с разрешением числа фотонов (PNR). Чтобы реализовать на основе находящихся в сжатом состоянии кубитов последовательность квантовых вентилей и сгенерировать запутанность между этими кубитами, данная последовательность импульсов поступает в большой интерферометр, состоящий из трёх сочленённых и динамически программируемых цикличных интерферометров. В каждом из трёх этих циклов содержатся важнейшие составляющие фотонного квантового компьютера: программируемый светоделитель, программируемый фазовращатель и оптоволоконная линия задержки; при работе со светом она выступает в качестве буферной памяти. Ключевые компоненты системы – это циклы, так как они позволяют притормаживать в оптоволоконной линии задержки каждый входящий импульс до тех пор, пока не поступит следующий импульс. Когда импульс приходит на вентиль светоделителя, этот вентиль может либо перебросить импульс в волокно (сохранить в памяти), либо перебросить из волокна (извлечь из памяти), либо выполнить запутывание импульса, извлечённого из цикла, со следующим входящим импульсом. Вот какая важная деталь касается трёх этих циклов: длительность задержки в них (соответственно, время хранения) – отличается. Второй вшестеро дольше первого, а третий вшестеро дольше второго. Такая геометрия позволяет продлить запутанность между находящимися в сжатом состоянии кубитами за пределы пары импульсов, следующих один за другим. В чисто пространственной архитектуре добиться такого было бы сложно. Пожалуй, слишком сложно представить все связи квантовой схемы Borealis, в том числе, всю соединяемость: дело в её размере и большом количестве вводов и выводов. Оптоволоконные линии задержки, расставленные на них светоделители и фазовращатели реализуют вентили как между смежными по времени, так и между отдалёнными модами. Эту структуру можно представить в виде трёхмерной решётки. Попробуем обрисовать, как Borealis переходит к синтезу всё более масштабных квантовых состояний. Первый цикл воплощает в одном измерении двухрежимные программируемые вентили между смежными по времени кубитами в сжатом состоянии, а второй и третий соответственно опосредуют вентили между кубитами в сжатом состоянии, которые разделены во втором и третьем измерении временными интервалами, соответственно, в 6 и 36 раз превышающими первый интервал. Последний этап работы Borealis – считывание. Измеряется, сколько фотонов в каждом из 216 выходных импульсов. Именно это мы и называем сэмплингом, и эта сложная задача, которая не поддаётся суперкомпьютеру, вполне эффективно решается при помощи квантовых состояний, генерируемых Borealis. Вот как, например, можно оценить, почему любому классическому компьютеру так сложно подготовить правильные образцы с правильно присвоенными вероятностями: представьте, какое огромное количество результатов может быть у эксперимента. Поскольку система находится в состоянии запутанности, вероятности исходов для каждого из этих 216 кубитов в сжатом состоянии не являются независимыми, и попытка реализовать подобное на классическом компьютере быстро выходит за рамки возможного. Вот замечательная картинка, позволяющая наглядно представить наш метод подсчёта фотонов. На футболке изображены восемь импульсов, каждый из которых соответствует своему фотонному событию (от 0 до 7). Эти события были измерены на одном из наших детекторов с разрешением числа фотонов. В Borealis для подсчёта фотонов задействуются высокочувствительные энергетические датчики. Они называются «детекторы с разрешением числа фотонов», сокращённо – PNR. Как только детектор поглощает входящий импульс света, энергия возрастает, и это приводит к серии электронных событий. Получается сигнал, пропорциональный амплитуде той энергии, что была поглощена детектором. Соответственно, чем выше записанный сигнал, тем выше была энергия конкретного импульса и, соответственно, тем больше в нём было фотонов. Амплитуды сигнала дискретизируются в соответствии с количеством детектированных фотонов, а наши аналитические приборы позволяют в точности извлекать эту информацию, замеряя электрические импульсы. PNR-детекторы – это единственная деталь Borealis, которую требуется при работе держать в криогене. Наши детекторы быстры, но ещё быстрее часы, регулирующие работу светоделителей и фазовращателей, а импульсы света в сжатом состоянии поступают слишком быстро. Поэтому современные PNR-детекторы не слишком точны в эксплуатации. Чтобы скомпенсировать этот разрыв в ходе часов, мы сконструировали демультиплексор. Задача демультиплексора – переупорядочивать последовательность импульсов света в сжатом состоянии, делая это при помощи сети оптических переключателей. Мы решили не использовать единственный PNR для выборки всех 216 входящих импульсов света в сжатом состоянии, а периодически распределять кубиты по 16 каналам, где они детектируются. Сканируя таким образом каналы считывания, мы можем ускорить часы в 16 раз по сравнению с тем, если бы они работали в канале каждого отдельного детектора. Можно привести аналогию: представьте себе аэропорт, где к одной таможенных конторок выстроилась целая очередь прибывших пассажиров. Насколько рациональнее было бы обслужить эту очередь силами 16 агентов. То же количество людей прошло бы через аэропорт гораздо быстрее.

? Практические варианты в эру NISQ

Много дискутируют о том, какое применение может найтись для квантовых компьютеров, которые можно будет собрать в ближайшем будущем. Этот класс машин называется «шумные квантовые компьютеры среднего масштаба» (NISQ). Что касается Borealis, любое такое применение должно будет вписываться в парадигму гауссова бозонного сэмплинга, то есть, иметь ограниченное приложение только при решении конкретного класса математических задач, касающихся вероятностных гафниановых распределений. Изучается, сколько потенциальных прикладных вариантов есть в данной области, и большинство из них соответствует задачам, которые можно выразить в графах. Граф – это сеть точек, соединённых рёбрами, где каждому ребру присвоен вес (числовое значение). Такие задачи естественно преобразуются в конкретное множество состояний и вентилей, предлагаемых Borealis.

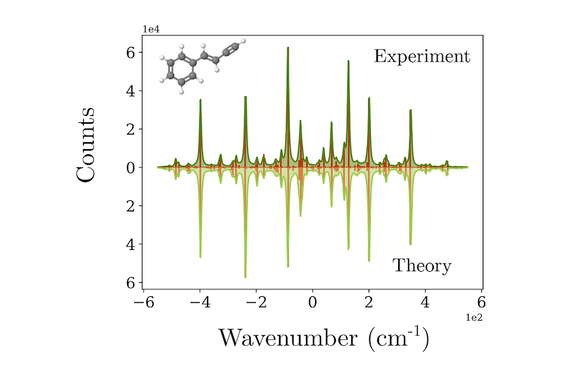
Маломасштабные демонстрации задач такого типа и ранее выполнялись в более ранних квантовых компьютерах, развёрнутых в облаке, в том числе, в системе X8, реализующей гауссов бозонный сэмплинг на 8 кубитах в сжатом состоянии. При помощи X8 удалось показать, что графы, относящиеся к разным структурным классам, можно эффективно различать: для этого их нужно запрограммировать на устройстве, а затем проанализировать распределение выходных значений. Таким образом можно запрограммировать упрощённую модель молекулы и вывести её вибронный спектр. Тот анализ на Borealis, что описан в этой статье, был призван дать математически однозначную демонстрацию квантового преимущества, для чего и программировались рандомизированные последовательности вентилей. Но демонстрации, в большей степени относящиеся к практической плоскости, как та, что была показана на X8, также заслуживают изучения, пусть и с иными ограничениями, касающимися конкретных деталей соединяемости Borealis и доступных параметров вентилей. Этот вопрос остаётся для самостоятельного изучения читателями, которые могут опробовать свои идеи прямо на облачном устройстве.

Вибронный спектр упрощённой модели молекулы, вычисленный при помощи гауссова бозонного сэмплинга на чипе X8 от Xanadu. Все-таки, как и со всеми машинами поколения NISQ, область применения такого компьютера остаётся ограниченной – и встаёт вопрос, можно ли добиться практического преимущества над имеющимися классическими техниками. Этот вопрос остаётся открытым. Причём, в среде исследователей, работающих как над аппаратным, так и над программным обеспечением квантовых компьютеров, ширится такое мнение: для полного раскрытия возможностей квантовых компьютеров нужно иметь представление о векторе технологического развития в более долгосрочной перспективе. В частности, учитывать возможность масштабирования до миллионов кубитов и исправлять ошибки, которые будут возникать при хранении и обработке квантовой информации – сейчас это одна из приоритетных целей аппаратных разработок в данной предметной области. Наряду со многими экспертами, занятыми разработкой оборудования и алгоритмов, авторы полагают, что нужны крупномасштабные и отказоустойчивые машины, которые позволили бы в полной мере оценить полезность квантовых вычислений.

? К практическим квантовым вычислениям: исправление ошибок и отказоустойчивость

Итак, каким же образом Borealis касается отказоустойчивых квантовых вычислений. Притом, что он прочно вписан в ландшафт устройств NISQ-эры, ряд разработанных для него и применяемых в нём технологий также являются критическими компонентами архитектуры для универсального отказоустойчивого квантового компьютера. В таком ракурсе работа по конструированию Borealis служит примером и вехой в развитии одной из этих основополагающих технологий в крайне требовательном контексте – то есть, в стремлении продемонстрировать квантовое преимущество при вычислениях. Важнейший образец такой технологии, интегрированной в Borealis и необходимой для отказоустойчивости – это использование стабилизированных оптоволоконных линий задержки, предназначенных для хранения в буферной памяти кубитов, пребывающих в сжатом состоянии. В предложенной отказоустойчивой архитектуре такая технология нужна, чтобы связать воедино большое квантовое состояние, где существует некоторая запутанность между кубитами, сгенерированными в разное время. Генерируя запутанность между кубитами, «рождёнными» в разное время, удаётся реализовать квантовые схемы большой глубины, при этом не распространяя каждый кубит через сопоставимое количество физических компонентов. Обходясь на аппаратном уровне без чрезмерно глубоких схем, мы сохраняем в архитектуре возможность диагностировать и исправлять ошибки по преодолении каждого вентиля и после каждого такта процессора. Запутать между собой кубиты из разных тактов процессора очень сложно, так как эта операция предполагает, что нам потребуется сохранить на протяжении целого тактового цикла машины кубит, циркулирующий в оптоволоконном кабеле. Поскольку свойства этих кубитов зависят от небольших флуктуаций (в масштабах нескольких нанометров) на всей длине их оптического распространения, требуются изощрённые приёмы стабилизации оптических циклов. Самый длинный из таких буферных циклов в Borealis превышает 1 км, что соответствует хранению информации в течение 6 микросекунд. Эта длина активно стабилизируется с фактической точностью до нескольких десятков нанометров – то есть, до одной части на 200 миллиардов. Всё равно, что стабилизировать кабель, проложенный от Ванкувера до Торонто до ширины человеческого волоса. Для описываемой отказоустойчивой архитектуры требуется хранить информацию примерно в течение 1 микросекунды – что соответствует паре сотен метров оптоволокна – поэтому весьма вдохновляет, что эти технологические разработки идут с опережением. Ещё один аспект отказоустойчивой архитектуры, реализованной в Borealis – это непосредственный синтез трёхмерной запутанности как таковой. Это лишний раз демонстрирует, с какой лёгкостью фотоника – опять же, всё благодаря использованию возможностей оптоволокна – применима для дальнодействующей соединяемости кубитов, созданных в физически удалённых точках. Дальнодействующая соединяемость, реализованная таким образом (что присуще именно фотонным архитектурам) позволяет задействовать более сложноорганизованные коды коррекции ошибок. Такие коды требуют запутанности между более удалёнными кубитами, чем обеспечивает «соединяемость с ближайшим соседом». Напротив, традиционные коды (например, код, учитывающий поверхность ошибки), для работы с которыми спроектированы сверхпроводниковые процессоры, ограничены именно соединяемостью с ближайшим соседом. Дальнодействующая соединяемость потенциально потребовала бы меньших издержек на кодирование логических кубитов с поправкой на ошибки в массивы необработанных физических кубитов.

Графическое представление трёхмерного запутанного состояния, синтезированного Borealis. Каждая вершина соответствует кубиту в сжатом состоянии, а каждое ребро представляет запутанность между теми вершинами, которые оно связывает. Зелёные, красные и голубые рёбра – это результат запутывания вентилей, реализованных в первом, втором и третьем цикле соответственно. Ряд других передовых свойств архитектуры, реализованных в Borealis, могут пригодиться в конструкции любой отказоустойчивой машины. В частности, имеются в виду изощрённые алгоритмы распознавания, используемые в детекторе фотонных импульсов (эти алгоритмы ускоряют работу детекторов). Также хороша система демультиплексирования, служащая ориентировочным прототипом подсистемы, которая повышала бы эксплуатационную надёжность отказоустойчивых источников кубитов. Наконец, есть отличная система программного управления, позволяющая автоматизировать выполнение больших и сложных квантовых схем. Все эти преимущества в комбинации с результатами дальнейшего оттачивания производительности интегрированных компонентов, нужных для синтеза и обработки отказоустойчивых кубитов, в большом масштабе должны сойтись и обеспечить создание по-настоящему практичного квантового компьютера.