#1 Нейронные сети для начинающих. Решение задачи классификации Ирисов Фишера

2022-08-10 17:15

Основы нейронных сетей, Нейронные сети для начинающих

На хабре было множество публикаций по данной теме, но все они говорят о разных вещах. Решил собрать всё в одну кучку и рассказать людям.
Это первая статья серии введения в нейронные сети, «Нейронные сети для начинающих». Здесь и далее мы постараемся разобраться с таким понятием — как нейронные сети, что они вообще из себя представляют и как с ними «подружиться», на практике решая простые задачи.

Что такое нейронные сети?

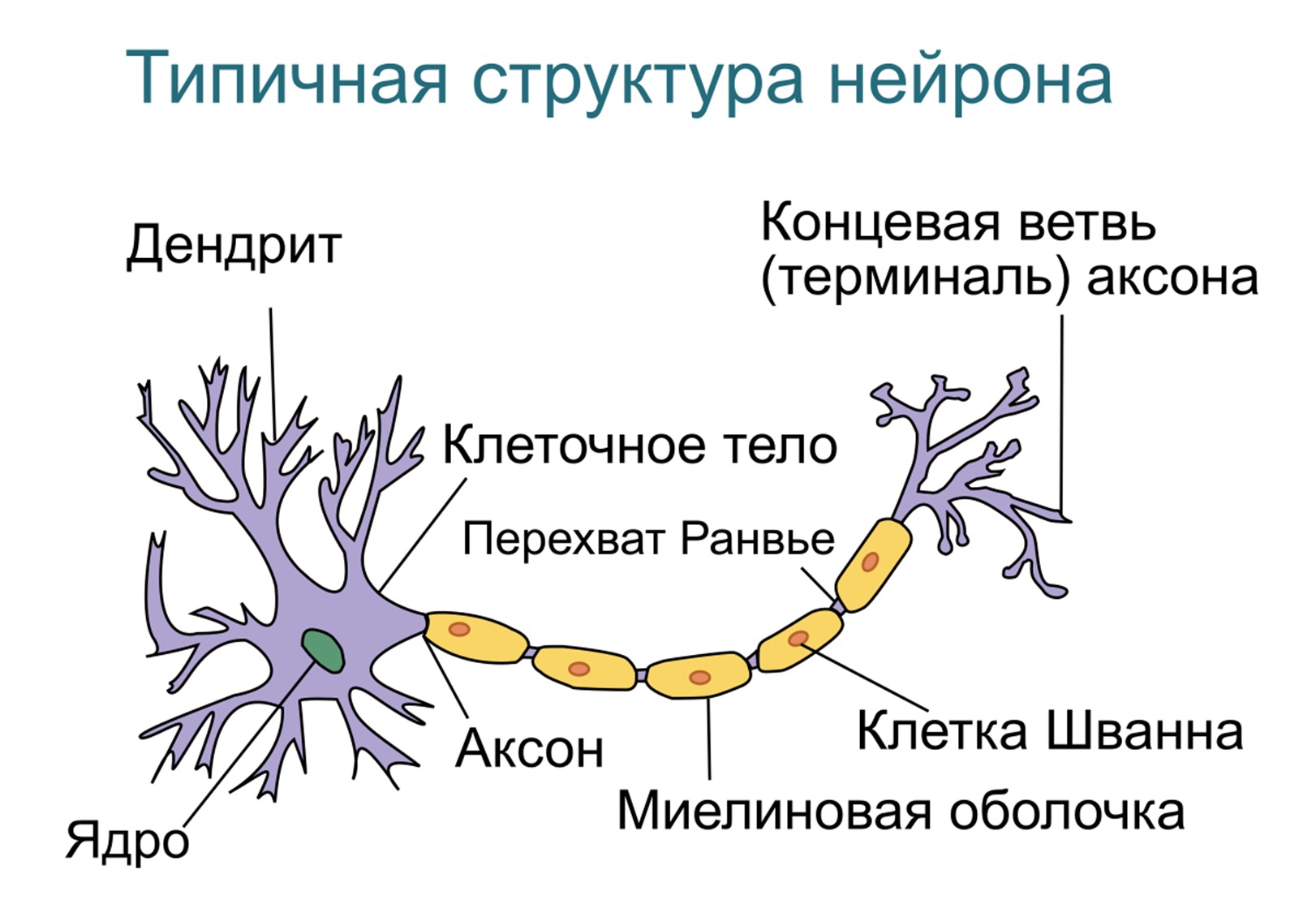
Нейро?нная сеть — математическая модель, а также её программное или аппаратное воплощение, построенная по принципу организации и функционирования биологических нейронных сетей — сетей нервных клеток живого организма (в частности, мозга).

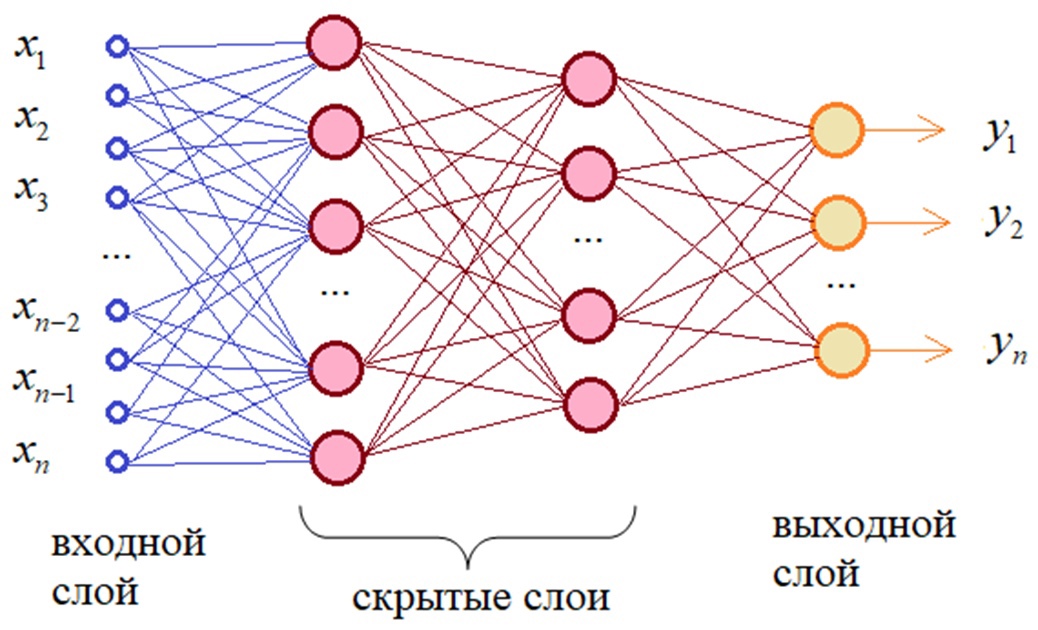
? Виды нейронных сетей:

Есть десятки видов нейросетей, которые отличаются архитектурой, особенностями функционирования и сферами применения. При этом чаще других встречаются сети трёх видов. Нейронные сети прямого распространения (Feed forward neural networks, FFNN). Прямолинейный вид нейросетей, при котором соседние узлы слоя не связаны, а передача информации осуществляется напрямую от входного слоя к выходному. FFNN имеют малую функциональность, поэтому часто используются в комбинации с сетями других видов. Свёрточные нейронные сети (Convolutional neural network, CNN). Состоят из слоёв пяти типов:

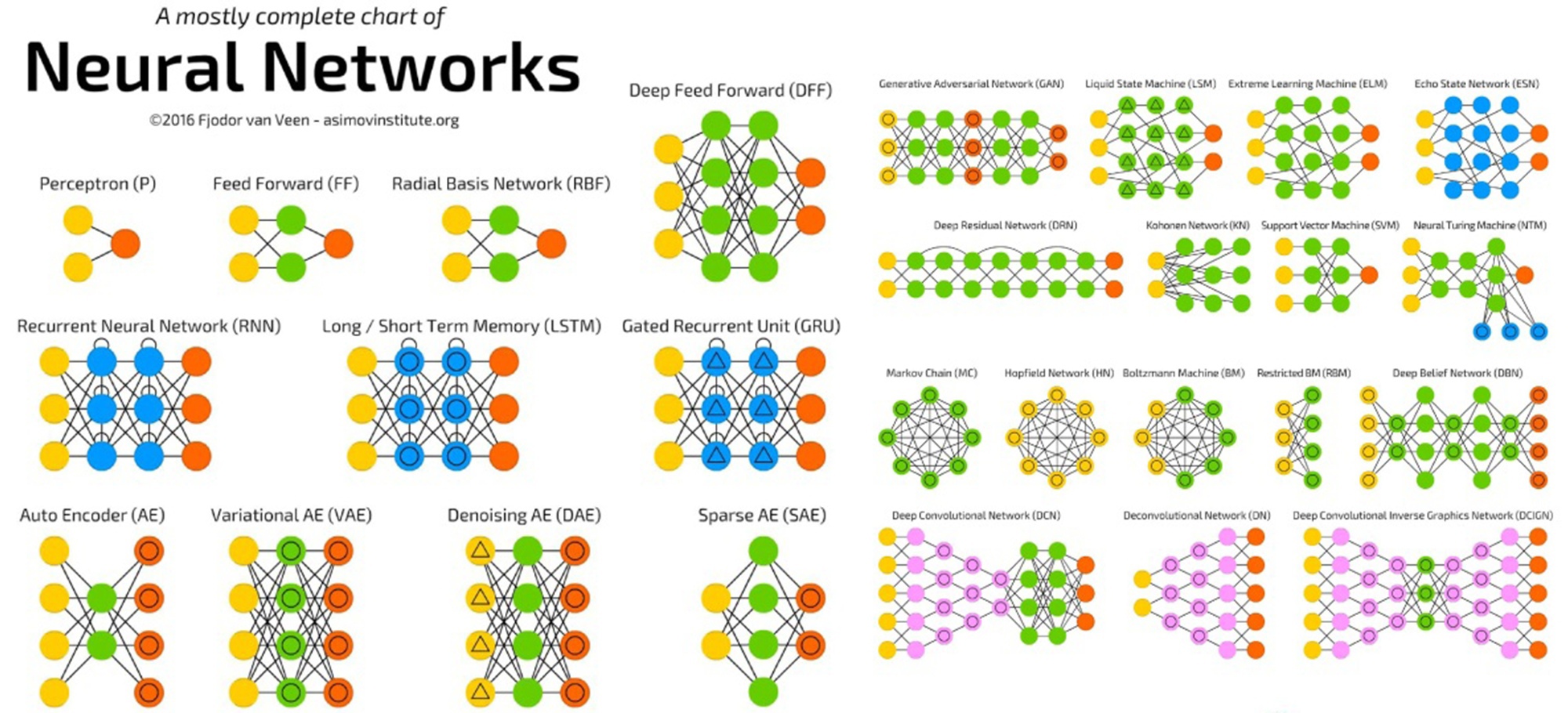
входного,
свёртывающего,
объединяющего,
подключённого,
выходного.

Каждый слой выполняет определённую задачу: например, обобщает или соединяет данные.

Свёрточные нейросети применяются для классификации изображений, распознавания объектов, прогнозирования, обработки естественного языка и других задач.

Рекуррентные нейронные сети (Recurrent neural network, RNN). Используют направленную последовательность связи между узлами. В RNN результат вычислений на каждом этапе используется в качестве исходных данных для следующего. Благодаря этому, рекуррентные нейронные сети могут обрабатывать серии событий во времени или последовательности для получения результата вычислений.

RNN применяют для языкового моделирования и генерации текстов, машинного перевода, распознавания речи и других задач.

? Типы задач, которые решают нейронные сети

Выделяют несколько базовых типов задач, для решения которых могут использоваться нейросети.

Классификация. Для распознавания лиц, эмоций, типов объектов: например, квадратов, кругов, треугольников. Также для распознавания образов, то есть выбора конкретного объекта из предложенного множества: например, выбор квадрата среди треугольников.
Регрессия. Для определения возраста по фотографии, составления прогноза биржевых курсов, оценки стоимости имущества и других задач, требующих получения в результате обработки конкретного числа.
Прогнозирования временных рядов. Для составления долгосрочных прогнозов на основе динамического временного ряда значений. Например, нейросети применяются для предсказания цен, физических явлений, объёма потребления и других показателей. По сути, даже работу автопилота Tesla можно отнести к процессу прогнозирования временных рядов.
Кластеризация. Для изучения и сортировки большого объёма неразмеченных данных в условиях, когда неизвестно количество классов на выходе, то есть для объединения данных по признакам. Например, кластеризация применяется для выявления классов картинок и сегментации клиентов.
Генерация. Для автоматизированного создания контента или его трансформации. Генерация с помощью нейросетей применяется для создания уникальных текстов, аудиофайлов, видео, раскрашивания чёрно-белых фильмов и даже изменения окружающей среды на фото.

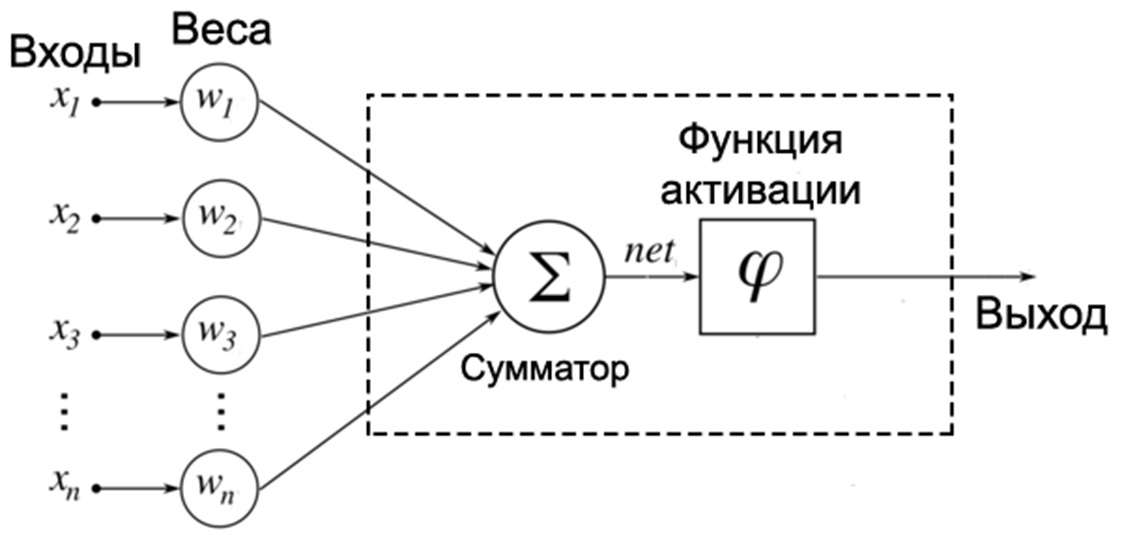
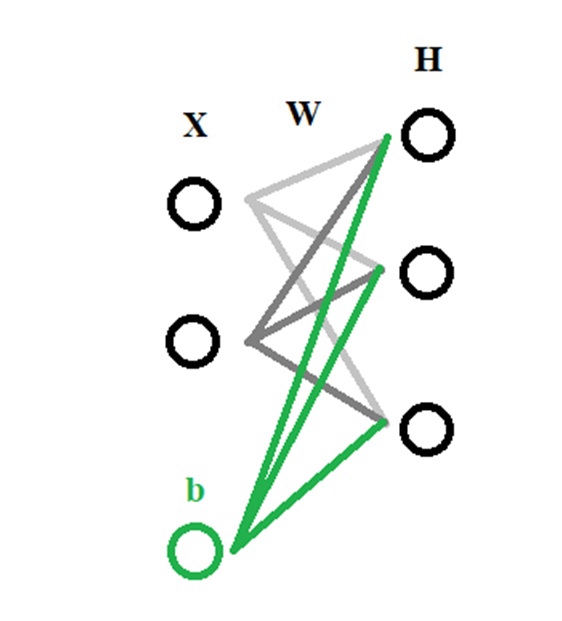
Как выглядит простая нейронная сеть?

Выяснив, как же она выглядит, мы перед тем, как разобрать её строение: что, зачем и почему — разберёмся, где же они применяются и что с помощью них можно сделать. Вот примерный список областей, где решение такого рода задач имеет практическое значение уже сейчас:

Экономика и бизнес.
Медицина и здравоохранение.
Авионика.
Связь.
Интернет.
Автоматизация производства.
Политологические и социологические исследования.
Безопасность, охранные системы.
Ввод и обработка информации.
Геологоразведка.
Компьютерные и настольные игры.
И т.д.

Теперь разберём подробнее самую простую модель искусственного нейрона — перцептрон:

Согласно общему определению перцептро?н или персептрон — математическая или компьютерная модель восприятия информации мозгом, предложенная Фрэнком Розенблаттом в 1958 году и впервые реализованная в виде электронной машины «Марк-1» в 1960 году. Перцептрон стал одной из первых моделей нейросетей, а «Марк-1» — первым в мире нейрокомпьютером.

Вы уже могли видеть подобные иллюстрации на просторах интернета:

Но что же это всё означает? Давайте по порядку: Х1, Х2, Х3, ..., Хn — входные классы, данные, которые мы подаём на вход нашей сети. Т.е. здесь у нас идут те данные, которые пришли к нам от клиента или же от нашего сервиса, который каким-то образом собирает/парсит данные , далее эти данные умножаются на случайные веса (стандартное обозначение W1, ..., Wn) и суммируются с так называемым нейроном смещения или bias нейрон в «Сумматоре» (из названия следует, что данные, Хn * Wn , суммируются друг с другом). Далее результат ?(Хn * Wn * b) подаётся в функцию активации, о которой поговорим далее.

Данные метаморфозы проиллюстрированы на следующем слайде:

? Задача классификации

Проговорив в общих чертах строение «базовой нейронной сети», плавно перейдём к рассмотрению задачи классификации — основной задачи нейронных сетей.

Итак, из определения следует, что классификация — это задача, при которой по некоторому объекту — исходные данные, нужно предсказать, к какому
классу объектов он принадлежит.

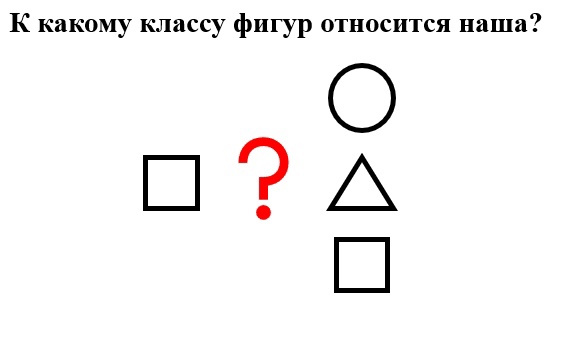
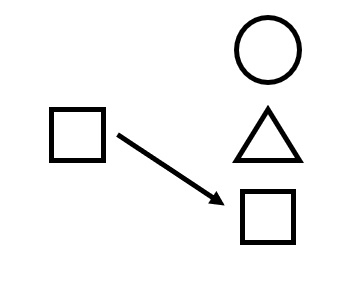
Примитивно эту задачу можно проиллюстрировать следующим образом:

Мы с вами, с лёгкостью можем понять, что ответ будет следующий:

Но а что на это скажет компьютер? Для него это лишь набор пикселей/байтов, который ему ни о чём не говорит. По-простому — это 0 и 1. Подробнее про это, можете почитать здесь. Для того, чтобы компьютер понял, что происходит внутри предложенных ему данных, мы должны «объяснить» ему всё и дать какой-то алгоритм, т.е. написать программу.

? Функции активации — ФА

Но это будет не просто программа, помимо базового кода, нам необходимо ввести так называемую математическую модель или же функцию активации, что же это такое?
Функция активации определяет выходное значение нейрона в зависимости от результата взвешенной суммы входов и порогового значения. Пример: ?=?(?).

Давайте рассмотрим некоторые распространённые ФА:

Первое, что приходит в голову, это вопрос о том, что считать границей активации для активационной функции. Если значение Y больше некоторого порогового значения, считаем нейрон активированным. В противном случае говорим, что нейрон неактивен. Такая схема должна сработать, но сначала давайте её формализуем. Функция А = активирована, если Y > граница, иначе нет. Другой способ: A = 1, если Y > граница, иначе А = 0.
Функция, которую мы только что создали, называется ступенчатой.

Функция принимает значение 1 (активирована), когда Y > 0 (граница), и значение 0 (не активирована) в противном случае.

Пользуясь определением, становится понятно, что ReLu возвращает значение х, если х положительно, и 0 в противном случае. ReLu нелинейна по своей природе, а комбинация ReLu также нелинейна! (На самом деле, такая функция является хорошим аппроксиматором, так как любая функция может быть аппроксимирована комбинацией ReLu). Это означает, что мы можем стэкать слои. Область допустимых значений ReLu — [ 0,inf ]. ReLu менее требовательно к вычислительным ресурсам, так как производит более простые математические операции. Поэтому имеет смысл использовать ReLu при создании глубоких нейронных сетей.

Сигмоида выглядит гладкой и подобна ступенчатой функции. Рассмотрим её преимущества. Во-первых, сигмоида — нелинейна по своей природе, а комбинация таких функций производит тоже нелинейную функцию. Ещё одно достоинство такой функции — она не бинарна, что делает активацию аналоговой, в отличие от ступенчатой функции. Для сигмоиды также характерен гладкий градиент. Если вы заметили, в диапазоне значений X от -2 до 2 значения Y меняется очень быстро. Это означает, что любое малое изменение значения X в этой области влечёт существенное изменение значения Y. Такое поведение функции указывает на то, что Y имеет тенденцию прижиматься к одному из краёв кривой.
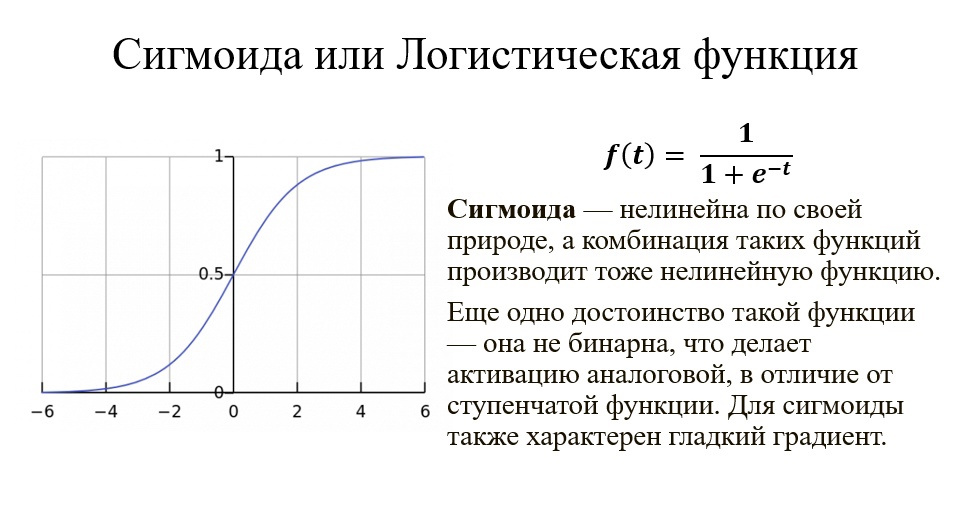
Сигмоида действительно выглядит подходящей функцией для задач классификации. Она стремится привести значения к одной из сторон кривой (например, к верхнему при х=2 и нижнему при х=-2). Такое поведение позволяет находить чёткие границы при предсказании.
Другое преимущество сигмоиды над линейной функцией заключается в следующем. В первом случае имеем фиксированный диапазон значений функции — [0,1], тогда как линейная функция изменяется в пределах (-inf, inf). Такое свойство сигмоиды очень полезно, так как не приводит к ошибкам в случае больших значений активации.

Сегодня сигмоида является одной из самых частых активационных функций в нейросетях.

Как же обучить нейронную сеть?

Теперь перейдём к другим немаловажным терминам.
Что нам понадобится:

Данные для обучения
Функция потерь
Понятие «градиентного спуска»

Цель обучения нейронной сети — найти такие параметры сети, при которых нейронная сеть будет ошибаться наименьшее количество раз.

Ошибка нейронной сети — отличие между предсказанным значением и правильным.

Самая простая функция потерь — Евклидово Расстояние или функция MSE:

$display$

yi – правильный результат.
zi – предсказанный результат.

Задача минимизации ошибки:

Используем метод оптимизации:

$display$

??????(?) — функция, возвращающая элемент вектора, где достигается минимум.
??????(?) — функция, возвращающая элемент вектора, где достигается максимум.

Градиентный спуск — метод нахождения локального минимума или максимума функции при помощи движения вдоль градиента.

Для вычисления градиентного спуска нам надо посчитать частные производные функции ошибки, по всем обучаемым параметрам нашей модели.

$??/??={ ??/(??_? ),??/(??_? ),??/(??_? ),…,??/(??_? ) }$

Пресловутые «Ирисы Фишера»

Теперь немного уйдём от голой теории и сделаем простую программу, решив базовую задачу классификации. Это базовая задача для специалистов, начинающих свой путь в нейронных сетях, своеобразный «Hello world!», для этого направления.

Здесь хотелось бы сделать небольшое отступление и рассказать подробнее про саму задачу «Ирисов Фишера» зачем и почему она здесь.

Ирисы Фишера — это набор данных для задачи классификации, на примере которого, Рональд Фишер в 1936 году продемонстрировал работу разработанного им метода дискриминантного анализа. Иногда его также называют ирисами Андерсона, так как данные были собраны американским ботаником Эдгаром Андерсоном. Этот набор данных стал уже классическим, и часто используется в литературе для иллюстрации работы различных статистических алгоритмов.

Вот так распределяются данные в датасете:

Ирисы Фишера состоят из данных о 150 экземплярах ириса, по 50 экземпляров из трёх видов:

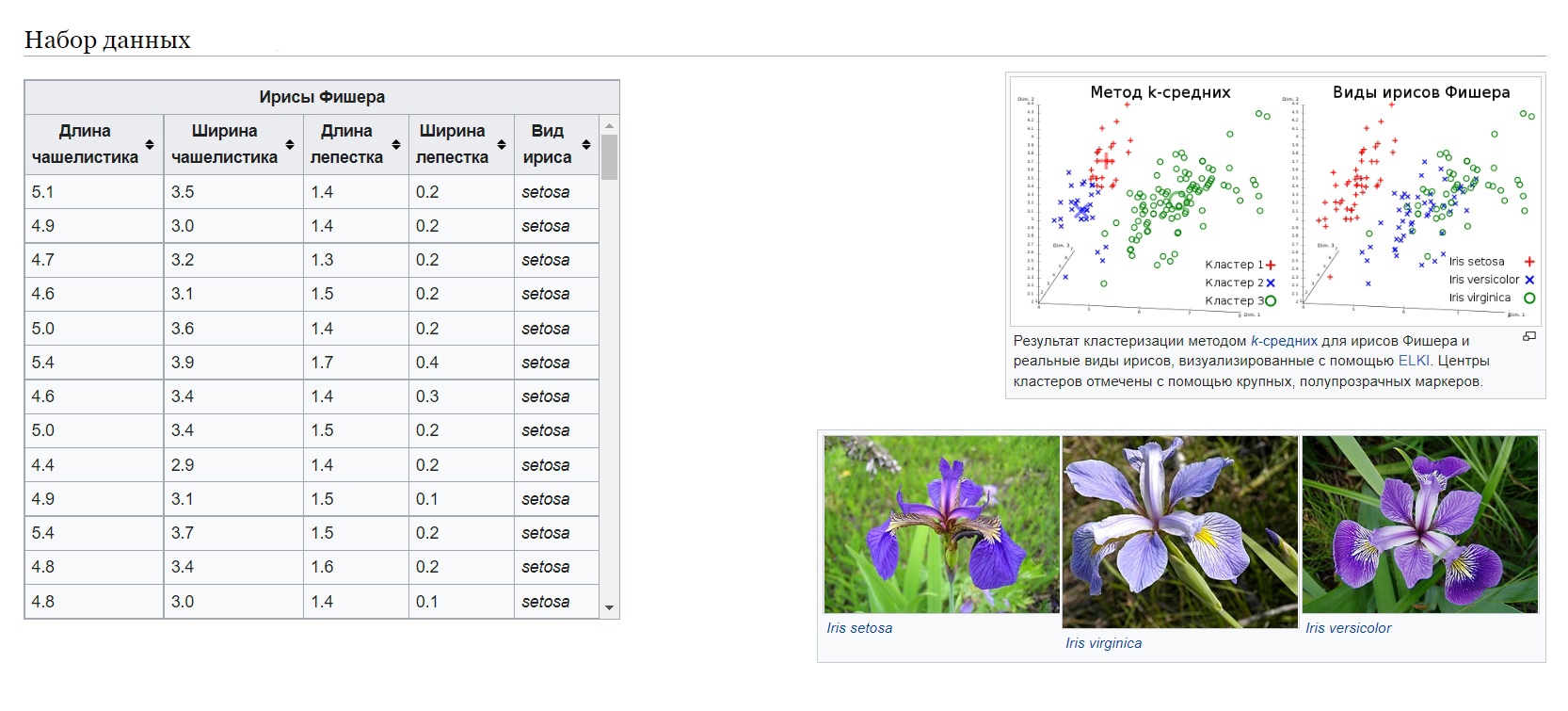
Ирис щетинистый (Iris setosa).
Ирис виргинский (Iris virginica).
Ирис разноцветный (Iris versicolor).

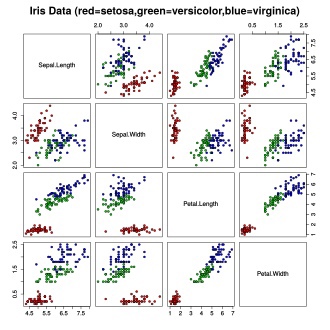
Для каждого экземпляра измерялись четыре характеристики (в сантиметрах):

Длина чашелистника (sepal length).
Ширина чашелистника (sepal width).
Длина лепестка (petal length).
Ширина лепестка (petal width).

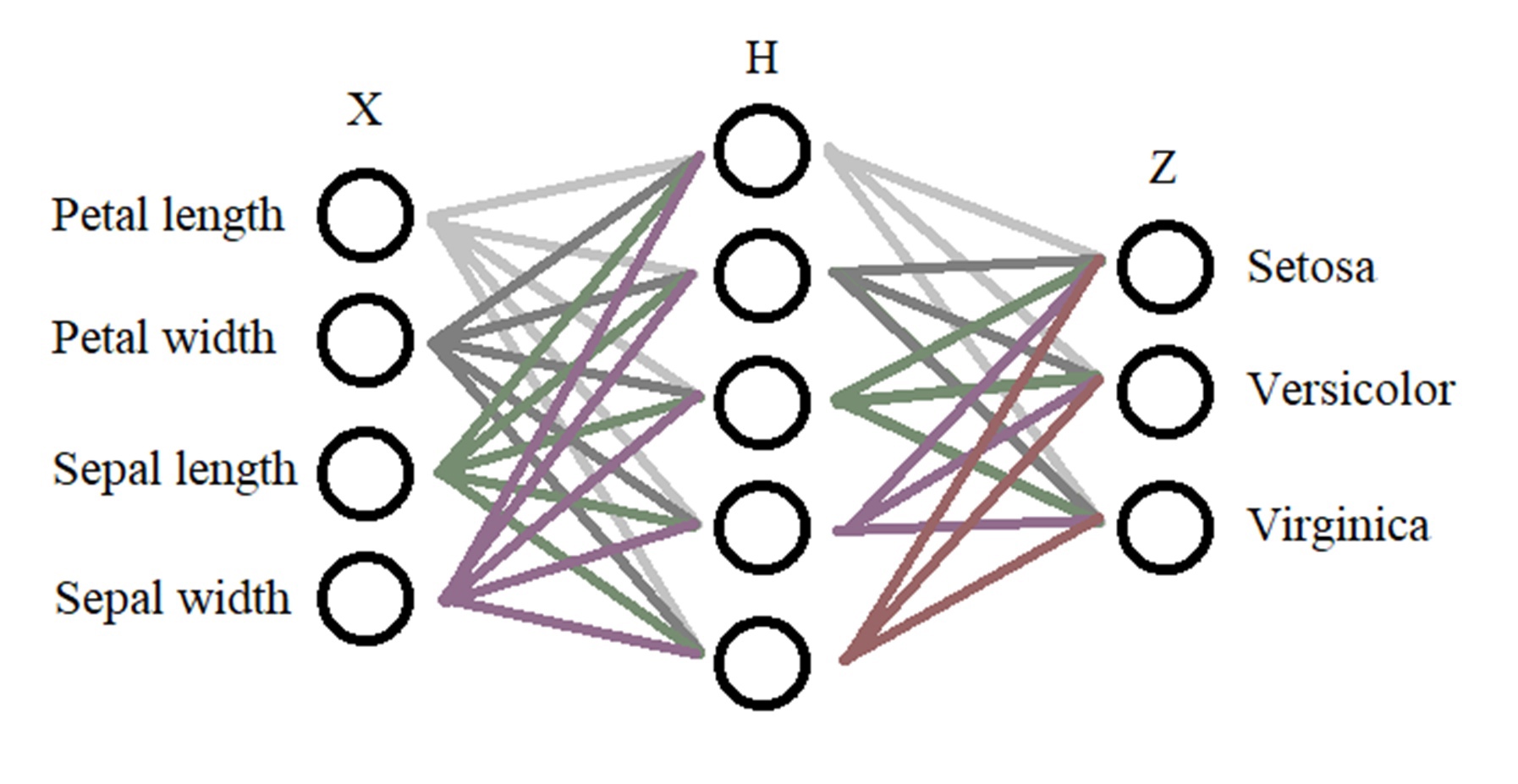
Конструкция нейронной сети:

На входе у нас есть 4 класса(характеристики) — Х, также нам понадобится всего один внутренний слой — Н, в нём будет 10 нейронов (выбирается методом подбора), далее на выходе мы имеем 3 класса, которые зависят от характеристики цветов — Z. Получается вот такая конструкция сети:

Далее распишем математическое обоснование для нашей задачи:

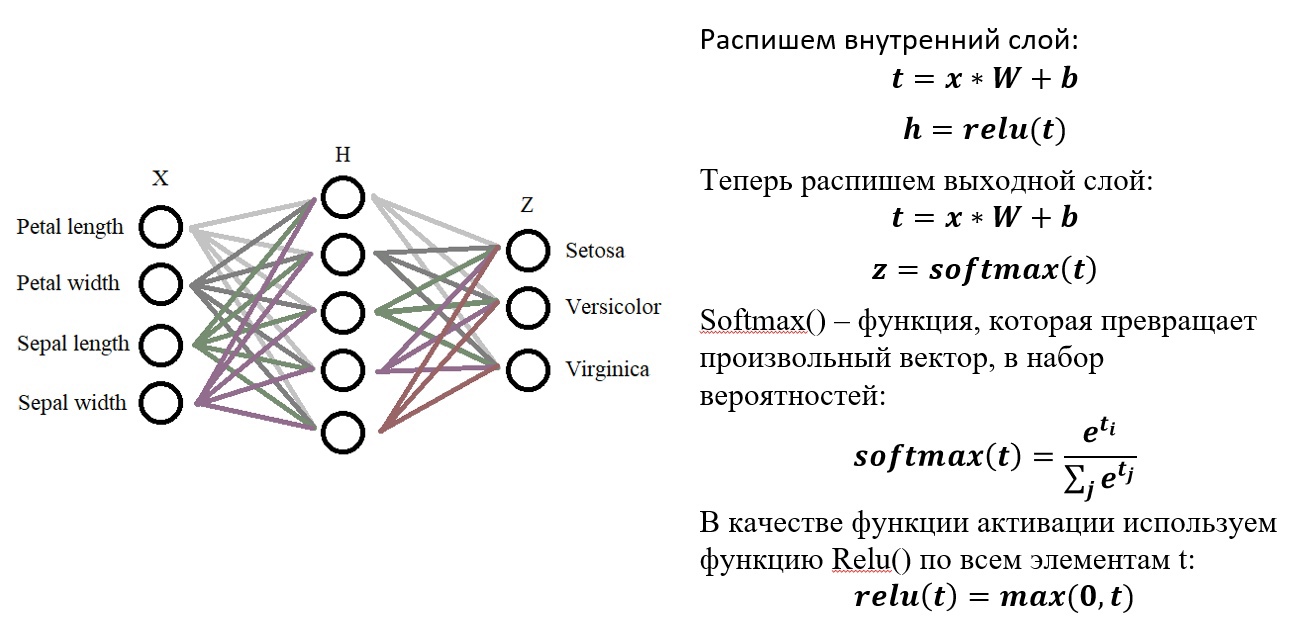
Ура-а-а-а! Наконец-то код!

Нам потребуется:

Язык программирования Python.
Базовая библиотека языка Python, для работы с линейными данными, NumPy.
Базовая библиотека языка Python, для «рандомизации» значений, random.

Для начала нам необходимо импортировать библиотеки numpy и random:

import numpy as np import random as rd

Теперь пропишем некоторые гиперпараметры:

INPUT_DIM = 4    #кол-во входных нейронов OUT_PUT = 3    #кол-во выходных нейронов H_DIM = 10     #кол-во нейронов в скрытом слое

Теперь зададим входной вектор и его веса (вначале рандомим данные, для получения реальной картины весов):

x = np.random.randn(INPUT_DIM) w1 = np.random.randn(INPUT_DIM, H_DIM) b1 = np.random.randn(H_DIM) w2 = np.random.randn(H_DIM, OUT_DIM) b2 = np.random.randn(OUT_DIM)

Расписываем вложенный слой — наше математическое обоснование:

t1 = x @ w1 + b1 h1 = relu(t1)

Точно также сделаем и для остальных.

Теперь обернём наш код в функцию:

def predict(x):     t1 = x @ W1 + b1     h1 = relu(t1)     t2 = h1 @ W2 + b2     z = softmax(t2)     print('z =', z)     return z

Оформим функцию relu():

def relu(t):     print('relu:', np.maximum(t, 0))     return np.maximum(t, 0)

Теперь добавим softmax():

def softmax(t):     out = np.exp(t)     print('softmax:', out / np.sum(out))     return out / np.sum(out)

Добавим вызов функции predict(), также class_names — имена выходных классов и вывод результатов предсказания:

probs = predict(x) pred_class = np.argmax(probs) class_names = ['Setosa', 'Versicolor', 'Virginica'] print('Predicted:', class_names[pred_class])

Наш код здесь нарандомит значения входных коэффициентов и весов, поэтому и результат будет случайный. Для тех, кто хочет весь код сразу:

import numpy as np import random as rd  INPUT_DIM = 4 OUT_DIM = 3 H_DIM = 10  x = [] for i in range(4):     x.append(float(input())) print(x)  # Рандомно вводим значения гиперпараметров: x = np.random.randn(INPUT_DIM) w1 = np.random.randn(INPUT_DIM, H_DIM) b1 = np.random.randn(H_DIM) w2 = np.random.randn(H_DIM, OUT_DIM) b2 = np.random.randn(OUT_DIM)  def relu(t):     print('relu:1', np.maximum(t, 0))     return np.maximum(t, 0)  def softmax(t):     out = np.exp(t)     print('softmax:', out / np.sum(out))     return out / np.sum(out)  def predict(x):     t1 = x @ w1 + b1     h1 = relu(t1)     t2 = h1 @ w2 + b2     z = softmax(t2)     print('z =1', z)     return z  tl = x @ w1 + b1 hl = relu(tl)  probs = predict(x) pred_class = np.argmax(probs) class_names = ['Setosa', 'Versicolor', 'Virginica'] print('Predicted:', class_names[pred_class])

Вот теперь добавим полученные после обучения веса и входные данные:

w1 = np.array([[ 0.33462099,  0.10068401,  0.20557238, -0.19043767,  0.40249301, -0.00925352,  0.00628916,  0.74784975,  0.25069956, -0.09290041 ], [ 0.41689589,  0.93211640, -0.32300143, -0.13845456,  0.58598293, -0.29140373, -0.28473491,  0.48021000, -0.32318306, -0.34146461 ], [-0.21927019, -0.76135162, -0.11721704,  0.92123373,  0.19501658,  0.00904006,  1.03040632, -0.66867859, -0.01571104, -0.08372566 ], [-0.67791724,  0.07044558, -0.40981071,  0.62098450, -0.33009159, -0.47352435,  0.09687051, -0.68724299,  0.43823402, -0.26574543 ]]) b1 = np.array([-0.34133575, -0.24401602, -0.06262318, -0.30410971, -0.37097632,  0.02670964, -0.51851308,  0.54665141,  0.20777536, -0.29905165 ]) w2 = np.array([[ 0.41186367,  0.15406952, -0.47391773 ], [ 0.79701137, -0.64672799, -0.06339983 ], [-0.20137522, -0.07088810,  0.00212071 ], [-0.58743081, -0.17363843,  0.93769169 ], [ 0.33262125,  0.18999841, -0.14977653 ], [ 0.04450406,  0.26168097,  0.10104333 ], [-0.74384144,  0.33092591,  0.65464737 ], [ 0.45764631,  0.48877246, -1.16928700 ], [-0.16020630, -0.12369116,  0.14171301 ], [ 0.26099978,  0.12834471,  0.20866959 ]]) b2 = np.array([-0.16286677,  0.06680119, -0.03563594 ])

Опять же для любителей всего кода в одном месте:

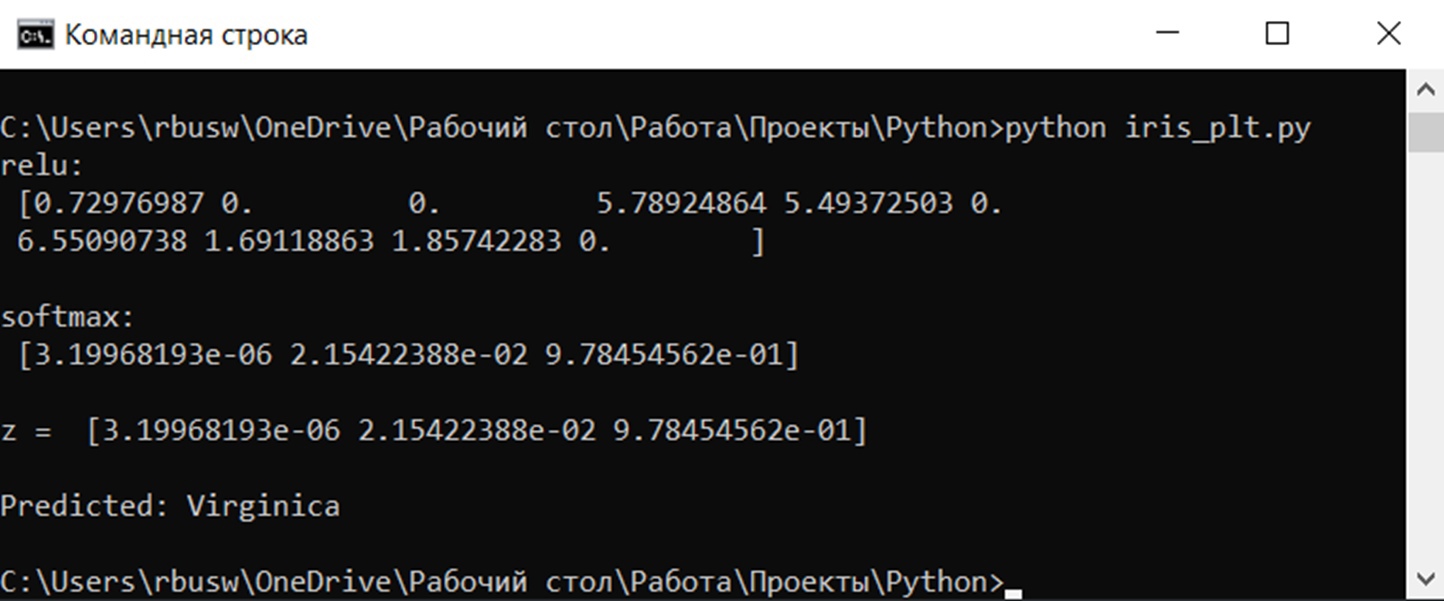
import numpy as np import random as rd  INPUT_DIM = 4 OUT_DIM = 3 H_DIM = 10  x = []  # Входные тестовые данные вводятся в следующем формате: "7.9 3.1 7.5 1.8" # Длина чашелистника: 7.9 # Ширина чашелистника: 3.1 # Длина лепестка: 7.5 # Ширина лепестка: 1.8  for i in range(4):     x.append(float(input())) print(x)  w1 = np.array([[ 0.33462099,  0.10068401,  0.20557238, -0.19043767,  0.40249301, -0.00925352,  0.00628916,  0.74784975,  0.25069956, -0.09290041 ], [ 0.41689589,  0.93211640, -0.32300143, -0.13845456,  0.58598293, -0.29140373, -0.28473491,  0.48021000, -0.32318306, -0.34146461 ], [-0.21927019, -0.76135162, -0.11721704,  0.92123373,  0.19501658,  0.00904006,  1.03040632, -0.66867859, -0.01571104, -0.08372566 ], [-0.67791724,  0.07044558, -0.40981071,  0.62098450, -0.33009159, -0.47352435,  0.09687051, -0.68724299,  0.43823402, -0.26574543 ]]) b1 = np.array([-0.34133575, -0.24401602, -0.06262318, -0.30410971, -0.37097632,  0.02670964, -0.51851308,  0.54665141,  0.20777536, -0.29905165 ]) w2 = np.array([[ 0.41186367,  0.15406952, -0.47391773 ], [ 0.79701137, -0.64672799, -0.06339983 ], [-0.20137522, -0.07088810,  0.00212071 ], [-0.58743081, -0.17363843,  0.93769169 ], [ 0.33262125,  0.18999841, -0.14977653 ], [ 0.04450406,  0.26168097,  0.10104333 ], [-0.74384144,  0.33092591,  0.65464737 ], [ 0.45764631,  0.48877246, -1.16928700 ], [-0.16020630, -0.12369116,  0.14171301 ], [ 0.26099978,  0.12834471,  0.20866959 ]]) b2 = np.array([-0.16286677,  0.06680119, -0.03563594 ])  # x = np.random.randn(INPUT_DIM) # w1 = np.random.randn(INPUT_DIM, H_DIM) # b1 = np.random.randn(H_DIM) # w2 = np.random.randn(H_DIM, OUT_DIM) # b2 = np.random.randn(OUT_DIM)  def relu(t):     print('relu:1', np.maximum(t, 0))     return np.maximum(t, 0)  def softmax(t):     out = np.exp(t)     print('softmax:', out / np.sum(out))     return out / np.sum(out)  def predict(x):     t1 = x @ w1 + b1     h1 = relu(t1)     t2 = h1 @ w2 + b2     z = softmax(t2)     print('z =1', z)     return z  tl = x @ w1 + b1 hl = relu(tl)  probs = predict(x) pred_class = np.argmax(probs) class_names = ['Setosa', 'Versicolor', 'Virginica'] print('Predicted:', class_names[pred_class])

И в итоге мы получим нужное нам предсказание

Полноценный код можно также посмотреть в моём github-репозитории по ссылке. Ну что же, мы с вами написали свой «Hello world» с нейронными сетями! Эта задача показывает одно из самых популярных направлений в DataSciense — направление классификации данных. Этим мы приоткрыли дверь в большой и быстроразвивающийся мир человекоподобных технологий. Дальше больше! А какие примеры классификации и интересные задачи из направления DataSciense вы знаете? Пишите свой вариант в комментариях!

Источник: habr.com

#1 Нейронные сети для начинающих. Решение задачи классификации Ирисов Фишера

Комментарии: