10 алгоритмов кластеризации с помощью Python

Он часто используется в качестве метода анализа данных для выявления интересных закономерностей в данных, таких как группы клиентов, основанные на их поведении.

Существует множество алгоритмов кластеризации на выбор, и нет единого наилучшего алгоритма кластеризации для всех случаев. Вместо этого рекомендуется изучить ряд алгоритмов кластеризации и различные конфигурации для каждого алгоритма.

В этом уроке вы узнаете, как подобрать и использовать лучшие алгоритмы кластеризации в python.

После завершения этого урока вы узнаете:

Кластеризация-это неконтролируемая проблема поиска естественных групп в пространстве признаков входных данных.
Существует множество различных алгоритмов кластеризации и нет единого наилучшего метода для всех наборов данных.
Как реализовать, адаптировать и использовать лучшие алгоритмы кластеризации в Python с помощью библиотеки машинного обучения scikit-learn.

Начните свой проект с моей новой книги "Мастерство машинного обучения с Python", включающей пошаговые руководства и файлы исходного кода Python для всех примеров.

Давайте начнем.

Обзор учебника

Этот учебник разделен на три части; они:

Кластеризация
Алгоритмы кластеризации
Примеры алгоритмов кластеризации
Установка библиотеки
Набор данных для кластеризации
Распространение Аффинности
Агломеративная кластеризация
БЕРЕЗА
DBSCAN
К-Означает
Мини-Партия K-Означает
Среднее Смещение
ОПТИКА
Спектральная кластеризация
Модель Гауссовой смеси

Кластеризация

Кластерный анализ, или кластеризация, - это задача машинного обучения без контроля.

Это включает в себя автоматическое обнаружение естественной группировки в данных. В отличие от контролируемого обучения (например, прогностического моделирования), алгоритмы кластеризации интерпретируют только входные данные и находят естественные группы или кластеры в пространстве объектов.

Методы кластеризации применяются, когда нет класса, который нужно предсказать, а скорее, когда экземпляры должны быть разделены на естественные группы.

— Страница 141, Интеллектуальный анализ данных: Практические инструменты и методы машинного обучения, 2016.

Кластер часто представляет собой область плотности в пространстве объектов, где примеры из области (наблюдения или строки данных) находятся ближе к кластеру, чем другие кластеры. Кластер может иметь центр (центроид), который является образцом или пространством точечных объектов, и может иметь границу или экстент.

Эти кластеры, по-видимому, отражают некоторый механизм, работающий в домене, из которого извлекаются экземпляры, механизм, который заставляет некоторые экземпляры иметь большее сходство друг с другом, чем с остальными экземплярами.

— Страницы 141-142, Интеллектуальный анализ данных: Практические инструменты и методы машинного обучения, 2016.

Кластеризация может быть полезна в качестве действия по анализу данных, чтобы узнать больше о проблемной области, так называемом обнаружении шаблонов или обнаружении знаний.

Например:

Филогенетическое дерево можно считать результатом ручного кластерного анализа.
Разделение нормальных данных от выбросов или аномалий может рассматриваться как проблема кластеризации.
Разделение кластеров на основе их естественного поведения является проблемой кластеризации, называемой сегментацией рынка.

Кластеризация также может быть полезна как тип проектирования объектов, где существующие и новые примеры могут быть сопоставлены и помечены как принадлежащие к одному из идентифицированных кластеров в данных.

Оценка выявленных кластеров является субъективной и может потребовать участия эксперта по предметной области, хотя существует множество количественных показателей, специфичных для кластеризации. Как правило, алгоритмы кластеризации сравниваются академически на синтетических наборах данных с заранее определенными кластерами, которые, как ожидается, обнаружит алгоритм.

Кластеризация-это метод обучения без контроля, поэтому трудно оценить качество результатов любого данного метода.

— Стр. 534, Машинное обучение: Вероятностная перспектива, 2012.

Алгоритмы кластеризации

Существует множество типов алгоритмов кластеризации.

Многие алгоритмы используют меры сходства или расстояния между примерами в пространстве объектов в попытке обнаружить плотные области наблюдений. Таким образом, часто рекомендуется масштабировать данные до использования алгоритмов кластеризации.

Центральным для всех целей кластерного анализа является понятие степени сходства (или различия) между отдельными объектами, которые группируются. Метод кластеризации пытается сгруппировать объекты на основе предоставленного ему определения сходства.

— Страница 502, Элементы статистического обучения: Интеллектуальный анализ данных, выводы и прогнозирование, 2016.

Некоторые алгоритмы кластеризации требуют, чтобы вы указали или предположили количество кластеров, которые необходимо обнаружить в данных, в то время как другие требуют указания некоторого минимального расстояния между наблюдениями, в которых примеры могут считаться “близкими” или “связанными”.

Таким образом, кластерный анализ представляет собой итерационный процесс, в ходе которого субъективная оценка идентифицированных кластеров возвращается в изменения конфигурации алгоритма до тех пор, пока не будет достигнут желаемый или соответствующий результат.

Библиотека scikit-learn предоставляет набор различных алгоритмов кластеризации на выбор.

Список из 10 наиболее популярных алгоритмов выглядит следующим образом:

Распространение Аффинности
Агломеративная кластеризация
БЕРЕЗА
DBSCAN
К-Означает
Мини-Партия K-Означает
Среднее Смещение
ОПТИКА
Спектральная кластеризация
Смесь гауссов

Каждый алгоритм предлагает свой подход к решению задачи обнаружения естественных групп в данных.

Не существует наилучшего алгоритма кластеризации и простого способа найти наилучший алгоритм для ваших данных без использования контролируемых экспериментов.

В этом уроке мы рассмотрим, как использовать каждый из этих 10 популярных алгоритмов кластеризации из библиотеки scikit-learn.

Приведенные примеры послужат основой для копирования и вставки примеров и тестирования методов на ваших собственных данных.

Мы не будем углубляться в теорию, лежащую в основе работы алгоритмов, или сравнивать их напрямую. Для хорошей отправной точки по этой теме см.:

Кластеризация, API scikit-learn.

Давайте погрузимся в это.

Примеры алгоритмов кластеризации

В этом разделе мы рассмотрим, как использовать 10 популярных алгоритмов кластеризации в scikit-learn.

Это включает в себя пример подгонки модели и пример визуализации результата.

Примеры предназначены для того, чтобы вы могли скопировать и вставить их в свой собственный проект и применить методы к своим собственным данным.

Установка библиотеки

Во-первых, давайте установим библиотеку.

Не пропустите этот шаг, так как вам нужно будет убедиться, что у вас установлена последняя версия.

Вы можете установить библиотеку scikit-learn с помощью установщика pip Python следующим образом:

sudo pip установите scikit-узнайте

1

sudo pip установите scikit-узнайте

Дополнительные инструкции по установке, относящиеся к вашей платформе, см. в разделе:

Установка scikit-узнайте

Затем давайте подтвердим, что библиотека установлена и вы используете современную версию.

Запустите следующий сценарий, чтобы распечатать номер версии библиотеки.

# проверьте scikit-изучите версию импорта печати sklearn(sklearn.__версия__)

1

2

3

# проверьте версию scikit-learn

импорт sklearn

печать(sklearn.__версия__)

Запустив пример, вы должны увидеть следующий номер версии или выше.

0.22.1

1

0.22.1

Набор данных для кластеризации

Мы будем использовать функцию make_classification() для создания тестового набора данных двоичной классификации.

Набор данных будет содержать 1000 примеров с двумя входными объектами и одним кластером на класс. Кластеры визуально видны в двух измерениях, так что мы можем построить данные с помощью точечной диаграммы и раскрасить точки на графике по назначенному кластеру. Это поможет увидеть, по крайней мере, в тестовой задаче, насколько “хорошо” были идентифицированы кластеры.

Кластеры в этой тестовой задаче основаны на многомерном гауссовском, и не все алгоритмы кластеризации будут эффективны при идентификации этих типов кластеров. Таким образом, результаты, приведенные в этом руководстве, не должны использоваться в качестве основы для сравнения методов в целом.

Ниже приведен пример создания и обобщения набора данных синтетической кластеризации

# synthetic classification dataset from numpy import where from sklearn.datasets import make_classification from matplotlib import pyplot # define dataset X, y = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # create scatter plot for samples from each class for class_value in range(2): # get row indexes for samples with this class row_ix = where(y == class_value) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show()

При выполнении примера создается набор данных синтетической кластеризации, затем создается точечная диаграмма входных данных с точками, окрашенными меткой класса (идеализированные кластеры).

Мы можем четко видеть две различные группы данных в двух измерениях, и есть надежда, что алгоритм автоматической кластеризации сможет обнаружить эти группировки.

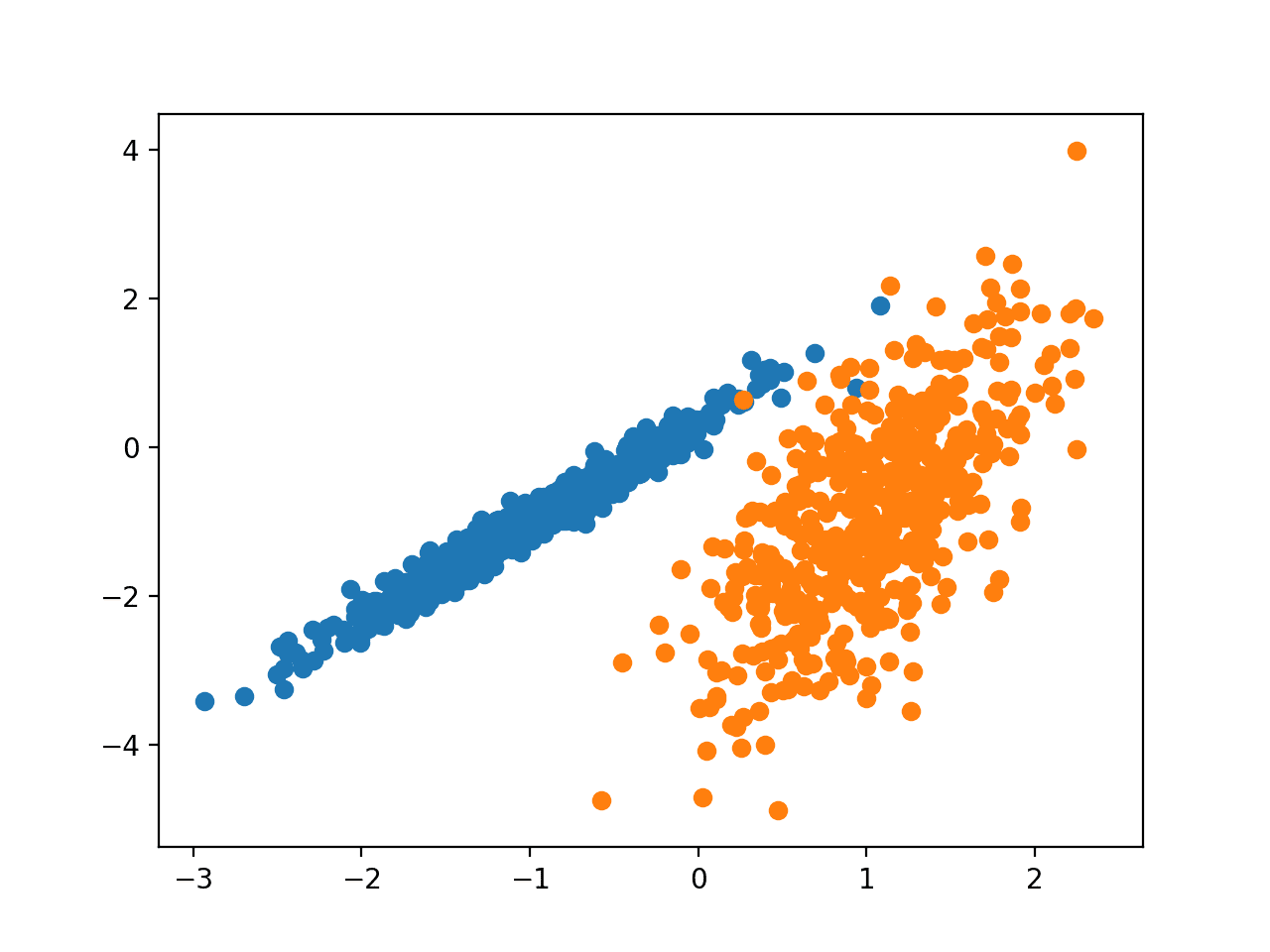
Точечная диаграмма набора данных синтетической кластеризации С точками, Окрашенными известным кластером

Затем мы можем начать рассматривать примеры алгоритмов кластеризации, применяемых к этому набору данных.

Я предпринял несколько минимальных попыток настроить каждый метод на набор данных.

Можете ли вы получить лучший результат для одного из алгоритмов?
Дайте мне знать в комментариях ниже.

Распространение Аффинности

Распространение сходства включает в себя поиск набора примеров, которые наилучшим образом обобщают данные.

Мы разработали метод, называемый “распространением сходства”, который принимает в качестве входных показателей сходство между парами точек данных. Между точками данных осуществляется обмен реальными сообщениями до тех пор, пока постепенно не появится высококачественный набор примеров и соответствующих кластеров

— Кластеризация путем передачи сообщений между точками данных, 2007.

Методика описана в статье:

Кластеризация путем передачи сообщений между точками Данных, 2007.

Он реализован с помощью класса Affinityprop, и основной настройкой для настройки является “демпфирование”, установленное в диапазоне от 0,5 до 1, и, возможно, “предпочтение”.

Полный пример приведен ниже.

# affinity propagation clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import AffinityPropagation from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = AffinityPropagation(damping=0.9) # fit the model model.fit(X) # assign a cluster to each example yhat = model.predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show()

Запуск примера соответствует модели в обучающем наборе данных и предсказывает кластер для каждого примера в наборе данных. Затем создается точечная диаграмма с точками, окрашенными в соответствии с назначенным им кластером.

В этом случае я не смог добиться хорошего результата.

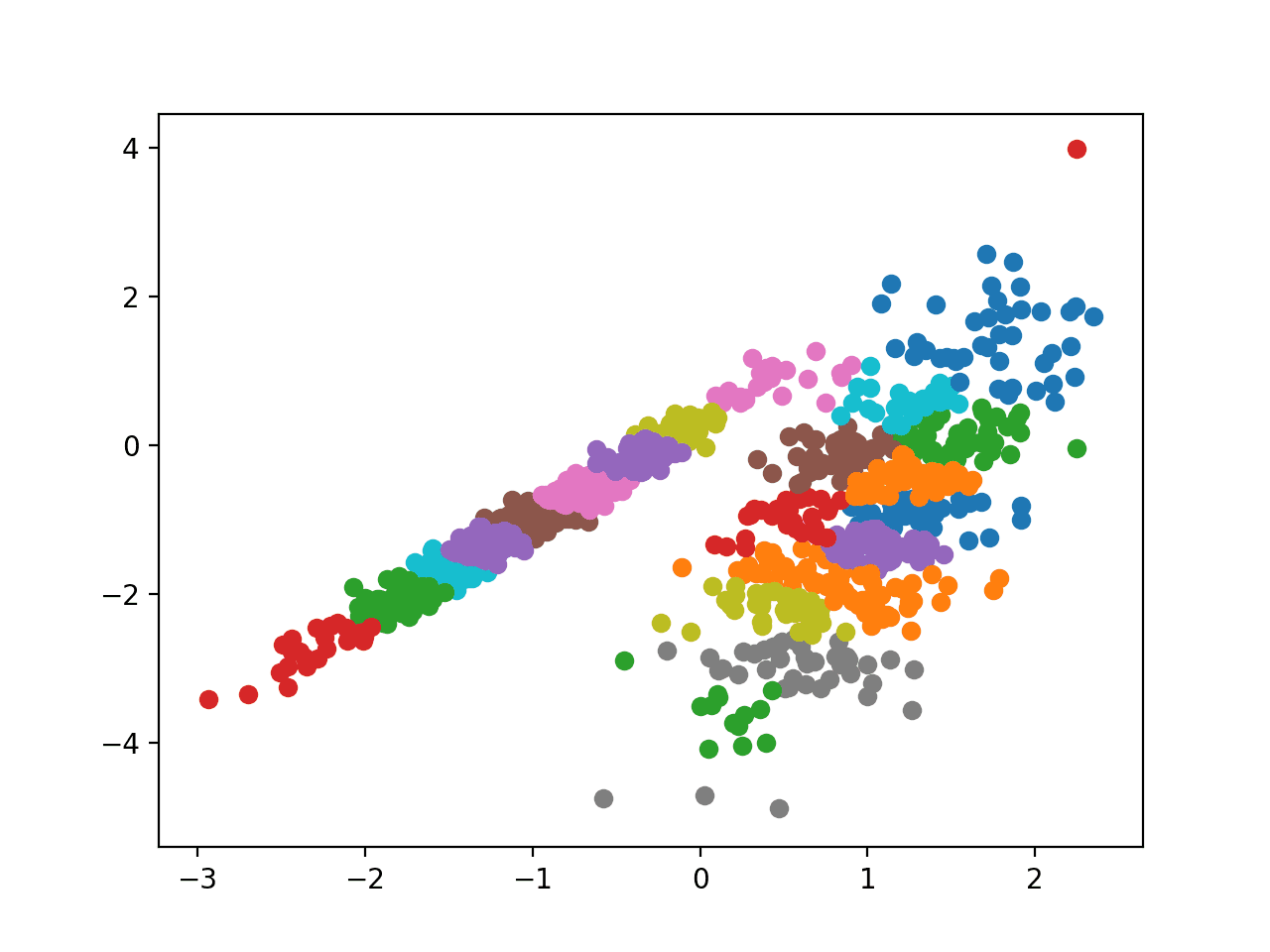
Точечная диаграмма набора данных С Кластерами, Идентифицированными С помощью Распространения сходства

Агломеративная кластеризация

Агломеративная кластеризация включает объединение примеров до тех пор, пока не будет достигнуто желаемое количество кластеров.

Это часть более широкого класса методов иерархической кластеризации, и вы можете узнать больше здесь:

Иерархическая кластеризация, Википедия.

Он реализован с помощью класса AgglomerativeClustering, и основной настройкой для настройки является набор “n_clusters”, оценка количества кластеров в данных, например 2.

Полный пример приведен ниже.

# agglomerative clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import AgglomerativeClustering from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = AgglomerativeClustering(n_clusters=2) # fit model and predict clusters yhat = model.fit_predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show()

Запуск примера соответствует модели в обучающем наборе данных и предсказывает кластер для каждого примера в наборе данных. Затем создается точечная диаграмма с точками, окрашенными в соответствии с назначенным им кластером.

В этом случае разумная группировка найдена.

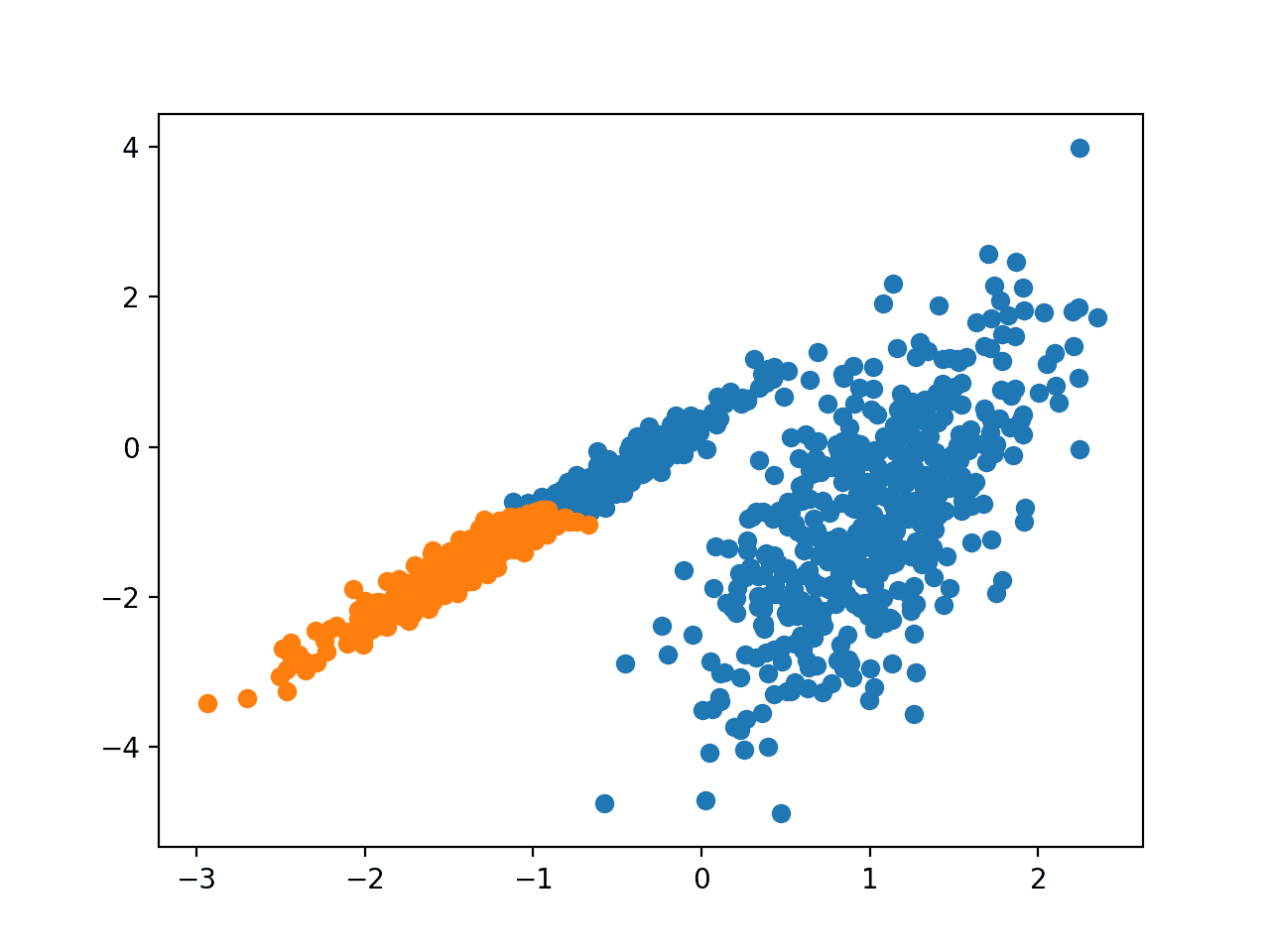
Точечная диаграмма набора данных С Кластерами, Идентифицированными С помощью Агломеративной кластеризации

БЕРЕЗА

Кластеризация БЕРЕЗЫ (БЕРЕЗА-сокращение от Сбалансированного итеративного сокращения и кластеризации с использованием
Иерархии) включает в себя построение древовидной структуры, из которой извлекаются центроиды кластеров.

BIRCH постепенно и динамически кластеризует входящие многомерные метрические данные, чтобы попытаться создать кластеризацию наилучшего качества с использованием доступных ресурсов (т. е. доступной памяти и ограничений по времени).

— BIRCH: Эффективный метод кластеризации данных для больших баз данных, 1996.

Методика описана в статье:

БЕРЕЗА: Эффективный метод кластеризации данных для больших баз данных, 1996.

Он реализован с помощью класса Birch, и основной конфигурацией для настройки являются гиперпараметры “порог” и “n_clusters”, последний из которых обеспечивает оценку количества кластеров.

Полный пример приведен ниже.

# birch clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import Birch from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = Birch(threshold=0.01, n_clusters=2) # fit the model model.fit(X) # assign a cluster to each example yhat = model.predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show()

Запуск примера соответствует модели в обучающем наборе данных и предсказывает кластер для каждого примера в наборе данных. Затем создается точечная диаграмма с точками, окрашенными в соответствии с назначенным им кластером.

В этом случае найдена отличная группировка.

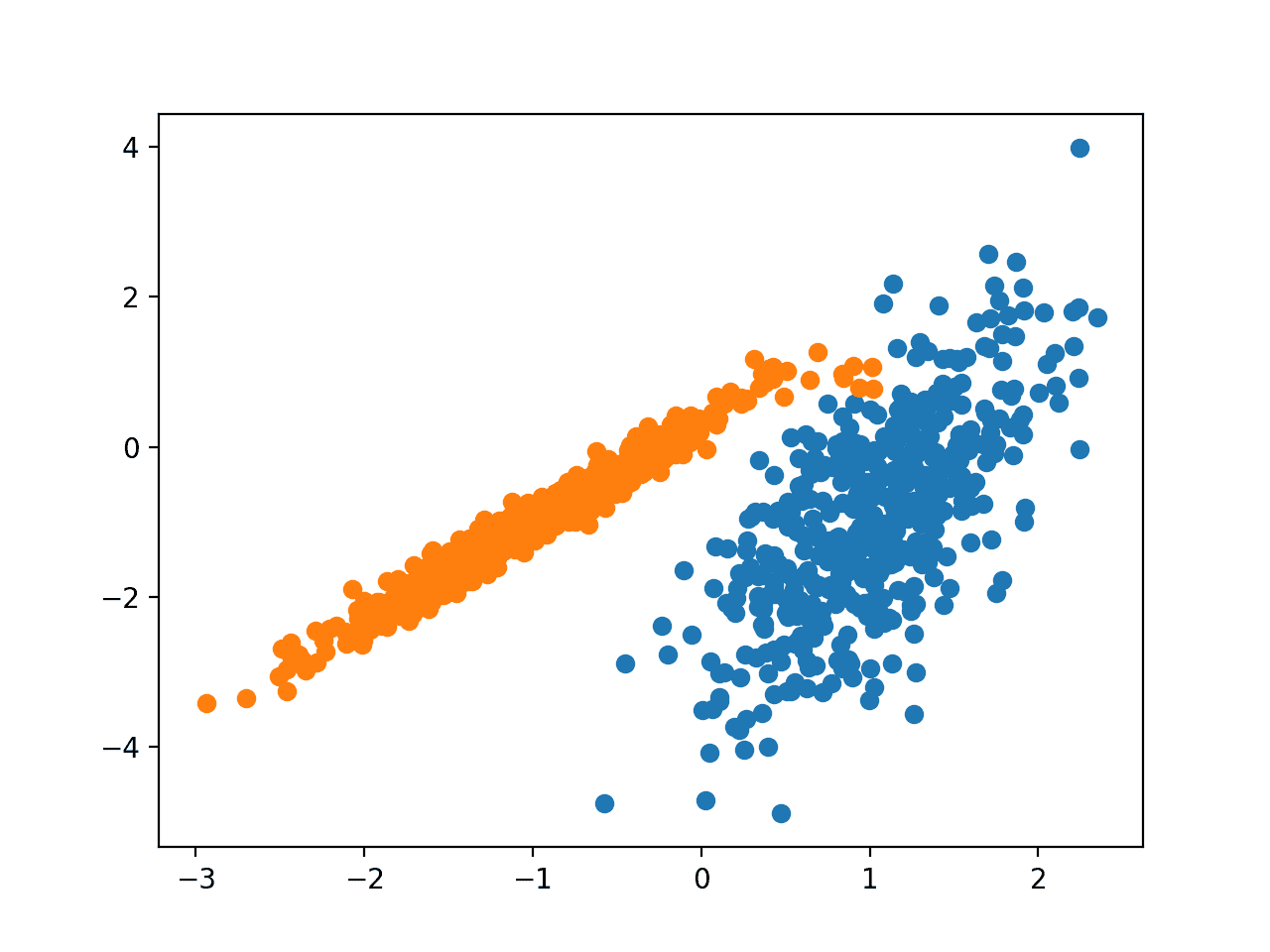
Точечная диаграмма набора данных С Кластерами, Идентифицированными С помощью кластеризации БЕРЕЗЫ

DBSCAN

Кластеризация DBSCAN (где DBSCAN-сокращение от пространственной кластеризации приложений с шумом на основе плотности) включает поиск областей высокой плотности в домене и расширение этих областей пространства объектов вокруг них в виде кластеров.

... мы представляем новый алгоритм кластеризации DBSCAN, основанный на понятии кластеров, основанном на плотности, который предназначен для обнаружения кластеров произвольной формы. DBSCAN требует только одного входного параметра и поддерживает пользователя в определении соответствующего значения для него

— Алгоритм на основе плотности для обнаружения кластеров в больших пространственных базах данных с шумом, 1996.

Методика описана в статье:

Алгоритм на основе плотности для обнаружения кластеров в больших пространственных базах данных с шумом, 1996.

Он реализован с помощью класса DBSCAN, и основной настройкой для настройки являются гиперпараметры “eps” и “min_samples".

Полный пример приведен ниже.

# dbscan clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import DBSCAN from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = DBSCAN(eps=0.30, min_samples=9) # fit model and predict clusters yhat = model.fit_predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show()

Запуск примера соответствует модели в обучающем наборе данных и предсказывает кластер для каждого примера в наборе данных. Затем создается точечная диаграмма с точками, окрашенными в соответствии с назначенным им кластером.

В этом случае найдена разумная группировка, хотя требуется дополнительная настройка.

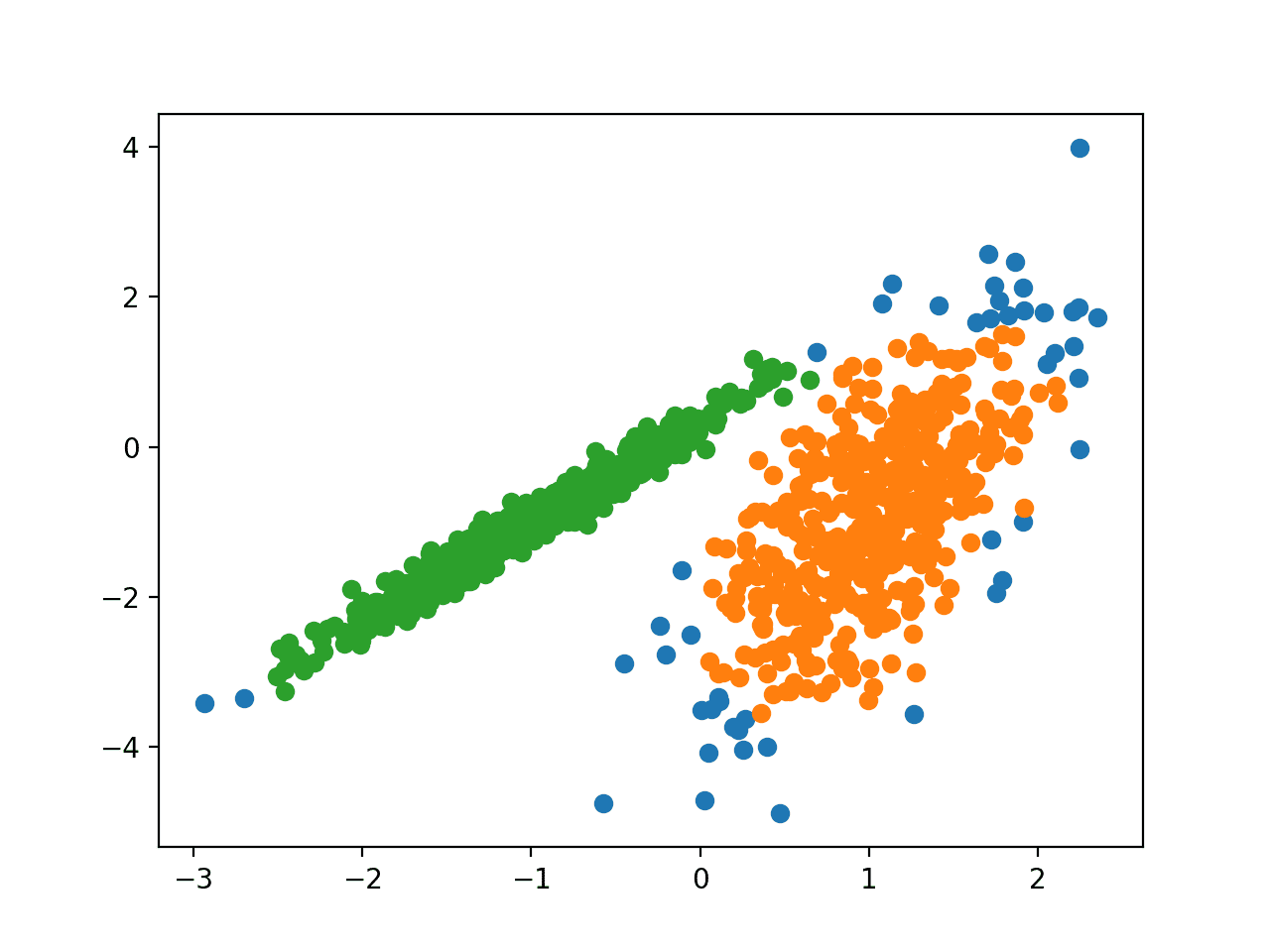
Точечная диаграмма набора данных С Кластерами, Идентифицированными С помощью кластеризации DBSCAN

К-Означает

Кластеризация K-средних может быть наиболее широко известным алгоритмом кластеризации и включает в себя назначение примеров кластерам в попытке минимизировать дисперсию внутри каждого кластера.

Основная цель этой статьи-описать процесс разбиения N-мерной совокупности на k множеств на основе выборки. Процесс, который называется "k-средними", по-видимому, дает разделы, которые достаточно эффективны в смысле различий внутри класса.

— Некоторые методы классификации и анализа многомерных наблюдений, 1967.

Методика описана здесь:

k-означает кластеризацию, Википедия.

Он реализован с помощью класса KMeans, и основной настройкой для настройки является гиперпараметр “n_clusters”, установленный для расчетного количества кластеров в данных.

Полный пример приведен ниже.

# k-means clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import KMeans from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = KMeans(n_clusters=2) # fit the model model.fit(X) # assign a cluster to each example yhat = model.predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show()

Запуск примера соответствует модели в обучающем наборе данных и предсказывает кластер для каждого примера в наборе данных. Затем создается точечная диаграмма с точками, окрашенными в соответствии с назначенным им кластером.

В этом случае найдена разумная группировка, хотя неравномерная равная дисперсия в каждом измерении делает метод менее подходящим для этого набора данных.

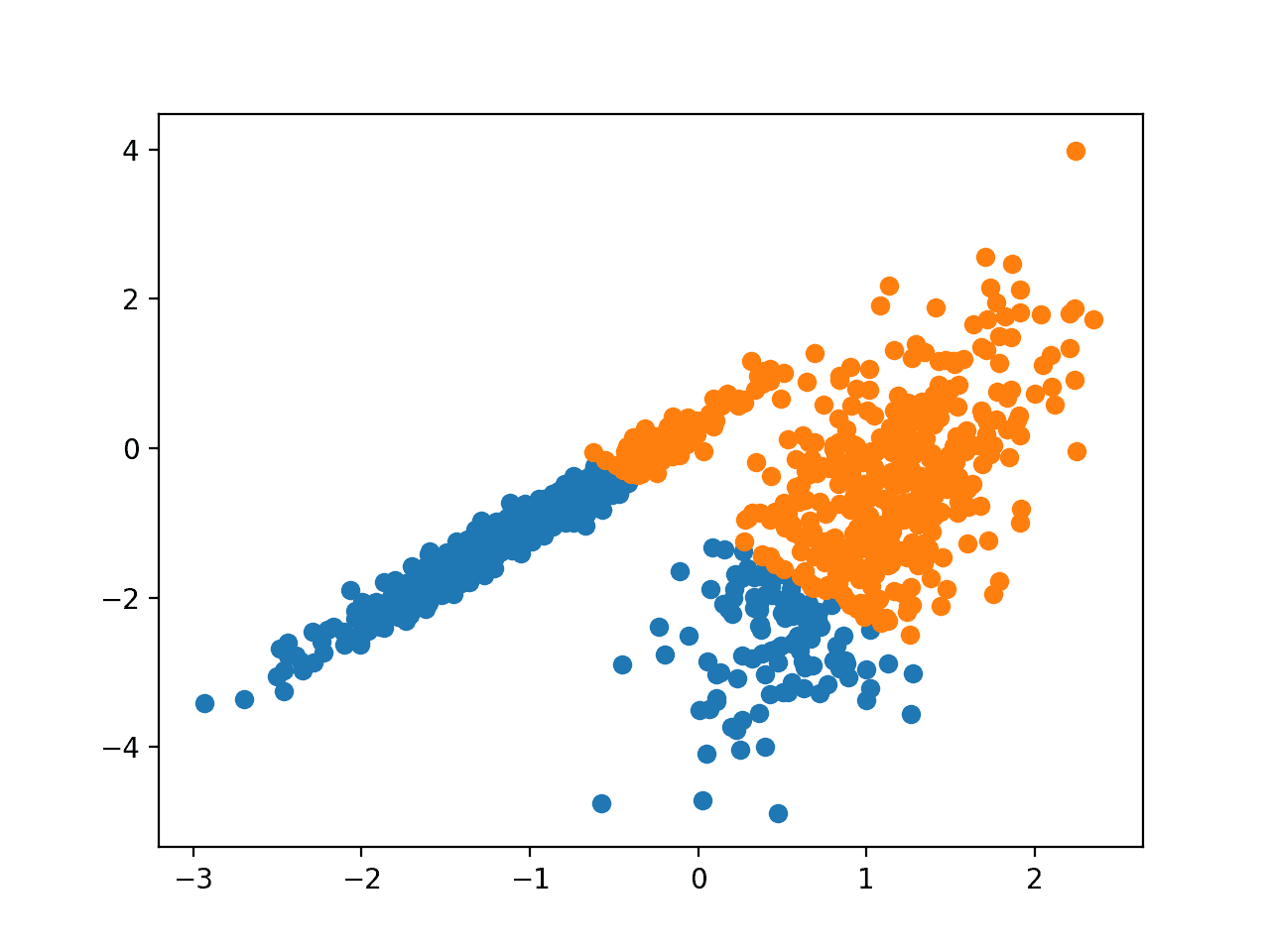
Точечная диаграмма набора данных С Кластерами, Идентифицированными С помощью Кластеризации K-Средних

Мини-Партия K-Означает

Мини-пакет K-Means-это модифицированная версия k-means, которая обновляет центроиды кластера с использованием мини-пакетов выборок, а не всего набора данных, что может ускорить работу с большими наборами данных и, возможно, повысить устойчивость к статистическому шуму.

... мы предлагаем использовать мини-пакетную оптимизацию для кластеризации k-средних. Это на порядки снижает затраты на вычисления по сравнению с классическим пакетным алгоритмом, обеспечивая при этом значительно лучшие решения, чем стохастический градиентный спуск в режиме онлайн.

— Кластеризация K-Средних в веб-масштабе, 2010.

Методика описана в статье:

Кластеризация K-Средних в веб-масштабе, 2010.

Он реализован с помощью класса MiniBatchKMeans, и основной настройкой для настройки является гиперпараметр “n_clusters”, установленный для расчетного количества кластеров в данных.

Полный пример приведен ниже.

# mini-batch k-means clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import MiniBatchKMeans from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = MiniBatchKMeans(n_clusters=2) # fit the model model.fit(X) # assign a cluster to each example yhat = model.predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show()

Запуск примера соответствует модели в обучающем наборе данных и предсказывает кластер для каждого примера в наборе данных. Затем создается точечная диаграмма с точками, окрашенными в соответствии с назначенным им кластером.

В этом случае будет найден результат, эквивалентный стандартному алгоритму k-средних.

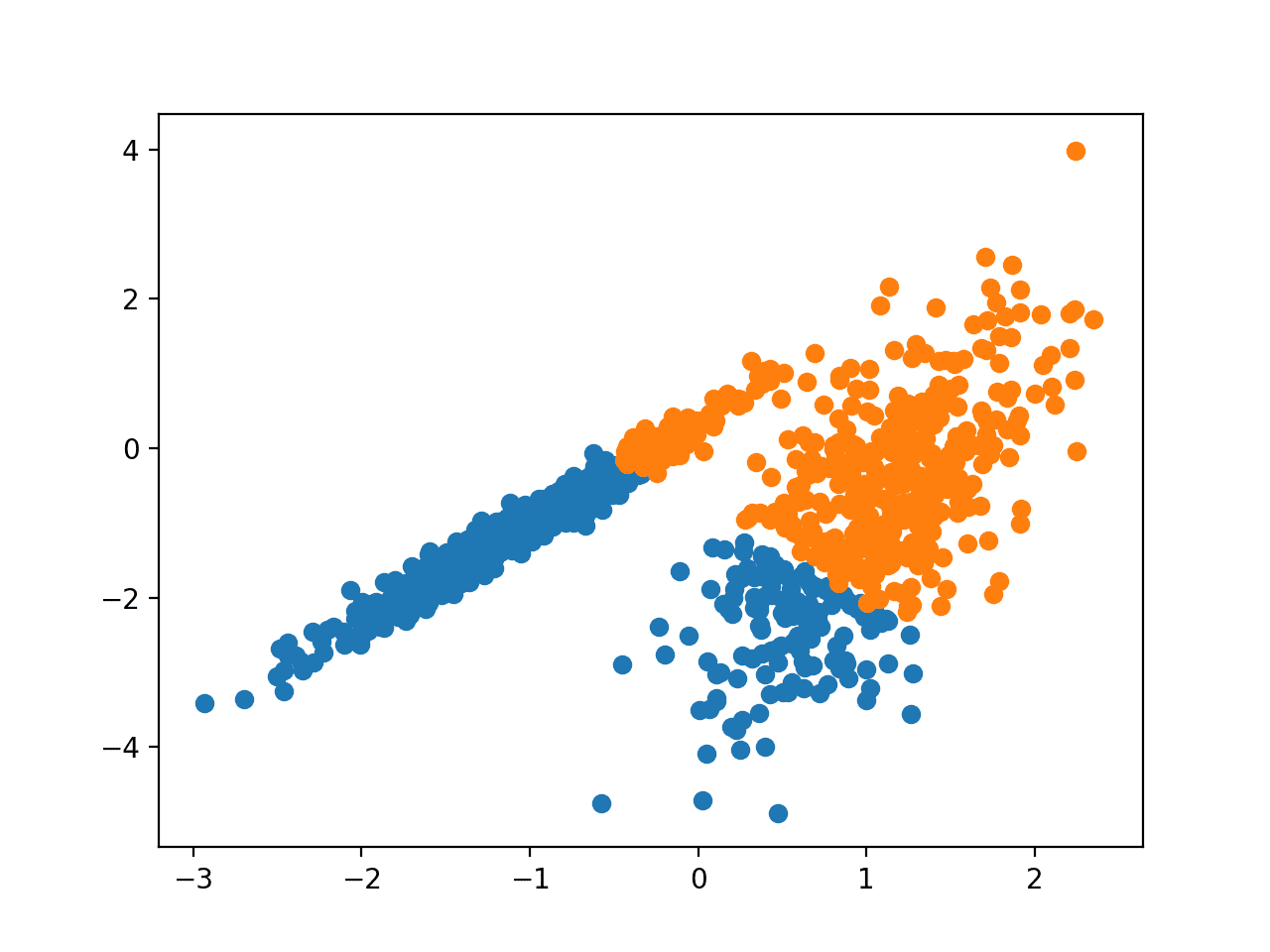
Точечная диаграмма набора данных С Кластерами, Идентифицированными С помощью Мини-Пакетной Кластеризации K-Средних

Среднее Смещение

Кластеризация среднего сдвига включает в себя поиск и адаптацию центроидов на основе плотности примеров в пространстве объектов.

Мы доказываем для дискретных данных сходимость рекурсивной процедуры среднего сдвига к ближайшей стационарной точке основной функции плотности и, следовательно, ее полезность для обнаружения режимов плотности.

— Средний сдвиг: надежный подход к анализу пространственных объектов, 2002.

Методика описана в статье:

Средний сдвиг: надежный подход к анализу пространственных объектов, 2002.

Он реализован с помощью класса MeanShift, и основной настройкой для настройки является гиперпараметр “пропускная способность”.

Полный пример приведен ниже.

# mean shift clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import MeanShift from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = MeanShift() # fit model and predict clusters yhat = model.fit_predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show()

Запуск примера соответствует модели в обучающем наборе данных и предсказывает кластер для каждого примера в наборе данных. Затем создается точечная диаграмма с точками, окрашенными в соответствии с назначенным им кластером.

В этом случае в данных содержится разумный набор кластеров.

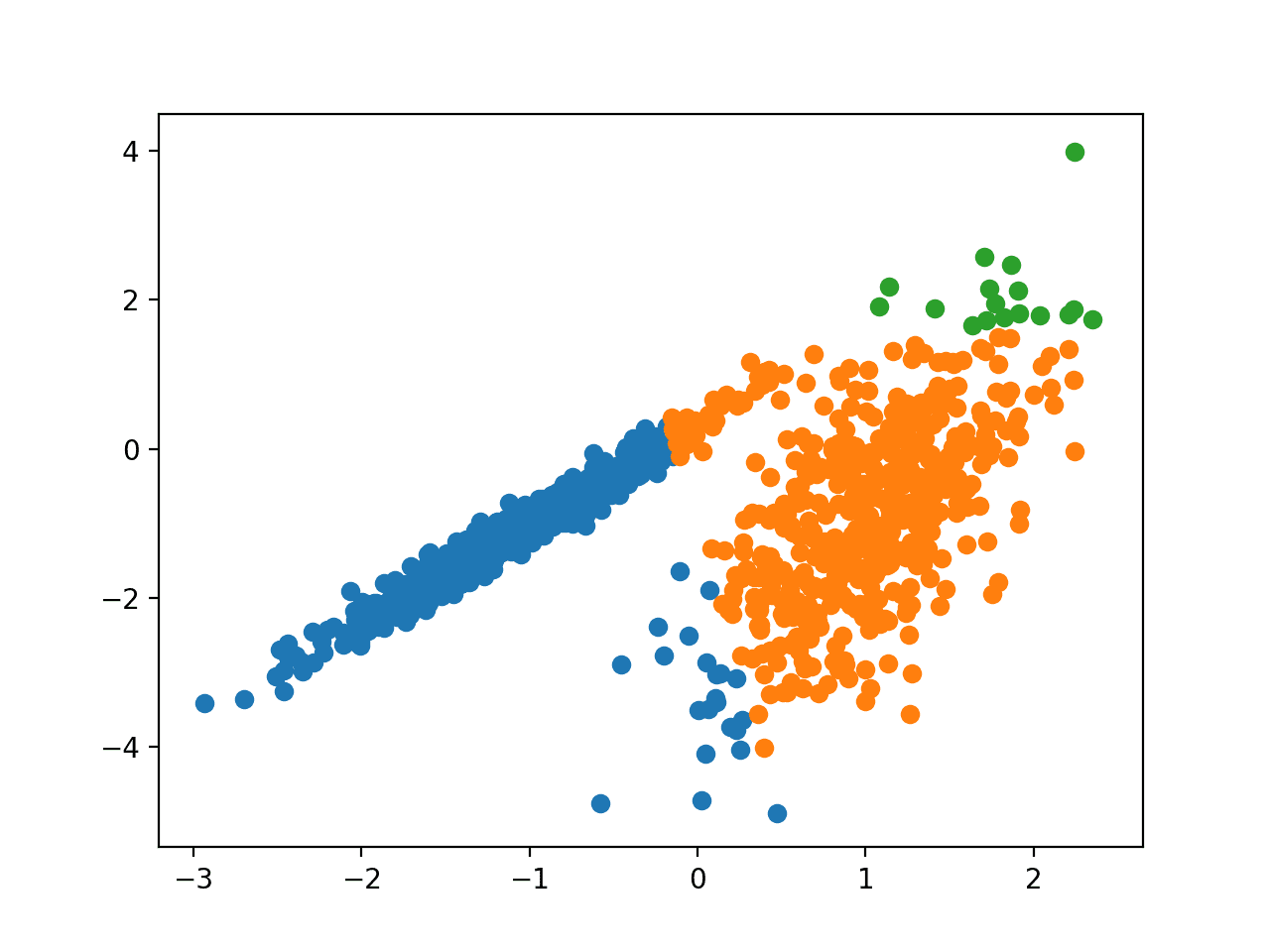
Точечная диаграмма набора данных С Кластерами, Идентифицированными С помощью Кластеризации среднего сдвига

ОПТИКА

Кластеризация ОПТИКИ (где ОПТИКА-сокращение от Точек упорядочения Для идентификации структуры кластеризации) - это модифицированная версия DBSCAN, описанная выше.

Мы вводим новый алгоритм для целей кластерного анализа, который не производит кластеризацию набора данных явно; вместо этого создается расширенный порядок базы данных, представляющий ее структуру кластеризации на основе плотности. Это кластерное упорядочение содержит информацию, эквивалентную кластеризации на основе плотности, соответствующей широкому диапазону настроек параметров.

— ОПТИКА: точки упорядочения для определения структуры кластеризации, 1999.

Методика описана в статье:

ОПТИКА: точки упорядочения для определения структуры кластеризации, 1999.

Он реализован с помощью класса OPTICS, и основной конфигурацией для настройки являются гиперпараметры “eps” и “min_samples".

Полный пример приведен ниже.

# optics clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import OPTICS from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = OPTICS(eps=0.8, min_samples=10) # fit model and predict clusters yhat = model.fit_predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show()

Запуск примера соответствует модели в обучающем наборе данных и предсказывает кластер для каждого примера в наборе данных. Затем создается точечная диаграмма с точками, окрашенными в соответствии с назначенным им кластером.

В этом случае я не смог добиться разумного результата по этому набору данных.

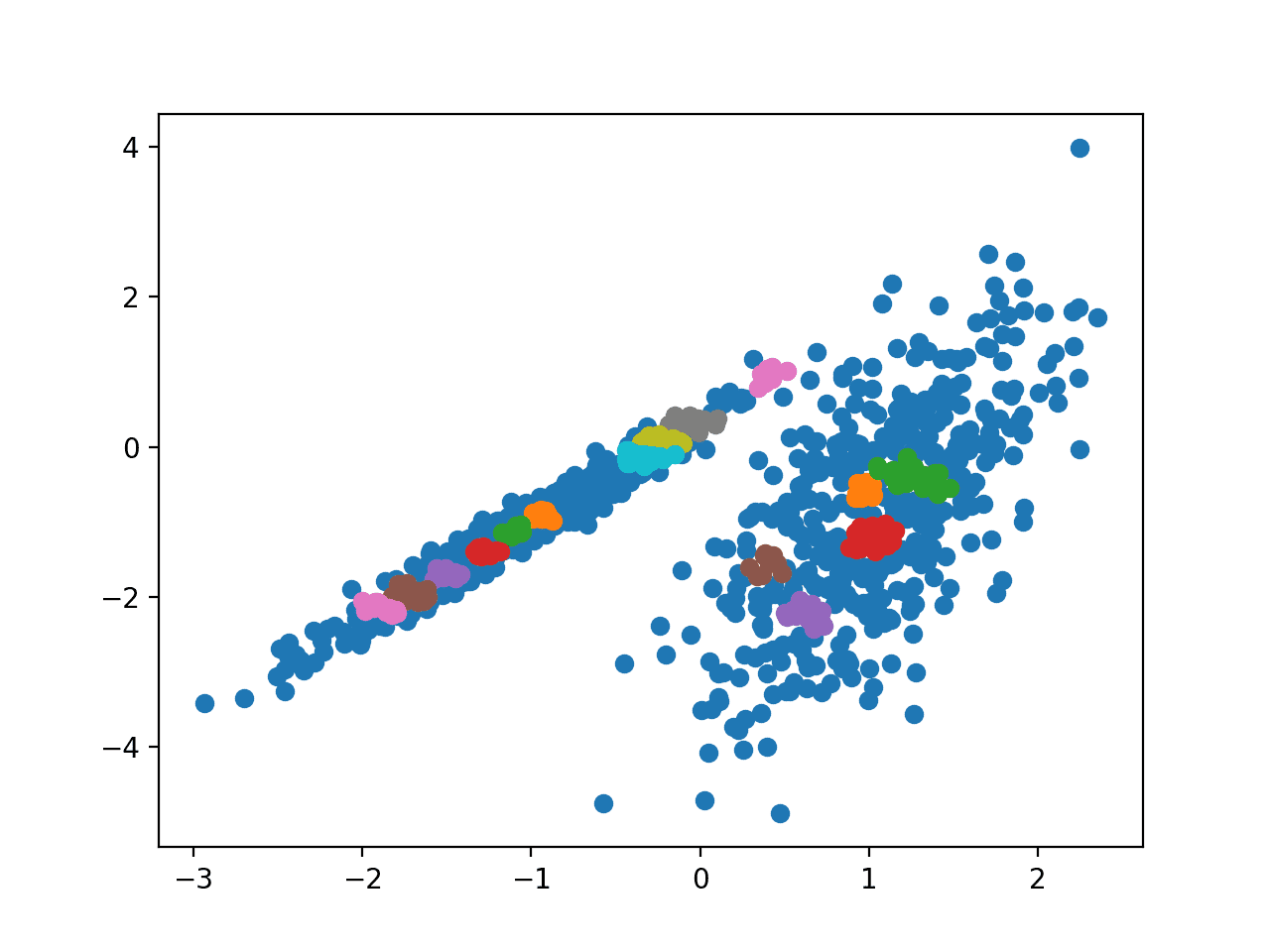
Точечная диаграмма набора данных С Кластерами, Идентифицированными С помощью кластеризации ОПТИКИ

Спектральная кластеризация

Спектральная кластеризация-это общий класс методов кластеризации, взятых из линейной алгебры.

Перспективной альтернативой, которая недавно появилась в ряде областей, является использование спектральных методов кластеризации. Здесь используются верхние собственные векторы матрицы, полученные из расстояния между точками.

— О спектральной кластеризации: Анализ и алгоритм, 2002.

Методика описана в статье:

О спектральной кластеризации: Анализ и алгоритм, 2002.

Он реализован с помощью класса SpectralClustering, а основная спектральная кластеризация-это общий класс методов кластеризации, взятых из линейной алгебры. для настройки используется гиперпараметр “n_clusters”, используемый для указания предполагаемого количества кластеров в данных.

Полный пример приведен ниже.

# spectral clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.cluster import SpectralClustering from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = SpectralClustering(n_clusters=2) # fit model and predict clusters yhat = model.fit_predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show()

Запуск примера соответствует модели в обучающем наборе данных и предсказывает кластер для каждого примера в наборе данных. Затем создается точечная диаграмма с точками, окрашенными в соответствии с назначенным им кластером.

В этом случае были найдены разумные кластеры.

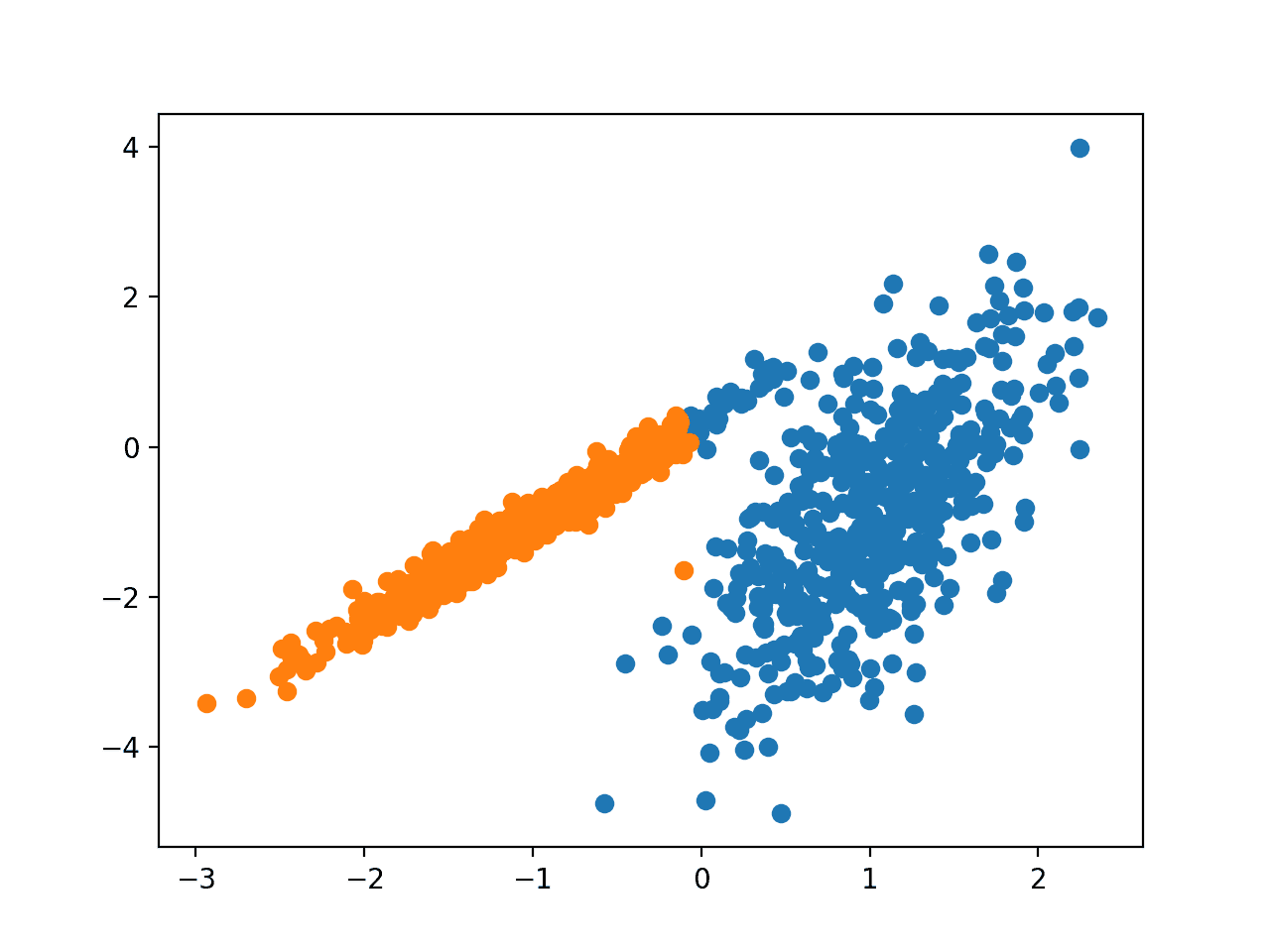
Точечная диаграмма набора данных С Кластерами, Идентифицированными С помощью Кластеризации спектров Кластеризация

Модель Гауссовой смеси

Модель гауссовой смеси суммирует многомерную функцию плотности вероятности со смесью гауссовых распределений вероятностей, как следует из ее названия.

Для получения дополнительной информации о модели см.:

Модель смеси, Википедия.

Он реализован с помощью класса GaussianMixture, и основной настройкой для настройки является гиперпараметр “n_clusters”, используемый для указания расчетного количества кластеров в данных.

Полный пример приведен ниже.

# gaussian mixture clustering from numpy import unique from numpy import where from sklearn.datasets import make_classification from sklearn.mixture import GaussianMixture from matplotlib import pyplot # define dataset X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2, n_redundant=0, n_clusters_per_class=1, random_state=4) # define the model model = GaussianMixture(n_components=2) # fit the model model.fit(X) # assign a cluster to each example yhat = model.predict(X) # retrieve unique clusters clusters = unique(yhat) # create scatter plot for samples from each cluster for cluster in clusters: # get row indexes for samples with this cluster row_ix = where(yhat == cluster) # create scatter of these samples pyplot.scatter(X[row_ix, 0], X[row_ix, 1]) # show the plot pyplot.show()

Запуск примера соответствует модели в обучающем наборе данных и предсказывает кластер для каждого примера в наборе данных. Затем создается точечная диаграмма с точками, окрашенными в соответствии с назначенным им кластером.

В этом случае мы видим, что кластеры были идентифицированы идеально. Это неудивительно, учитывая, что набор данных был создан как смесь гауссов.

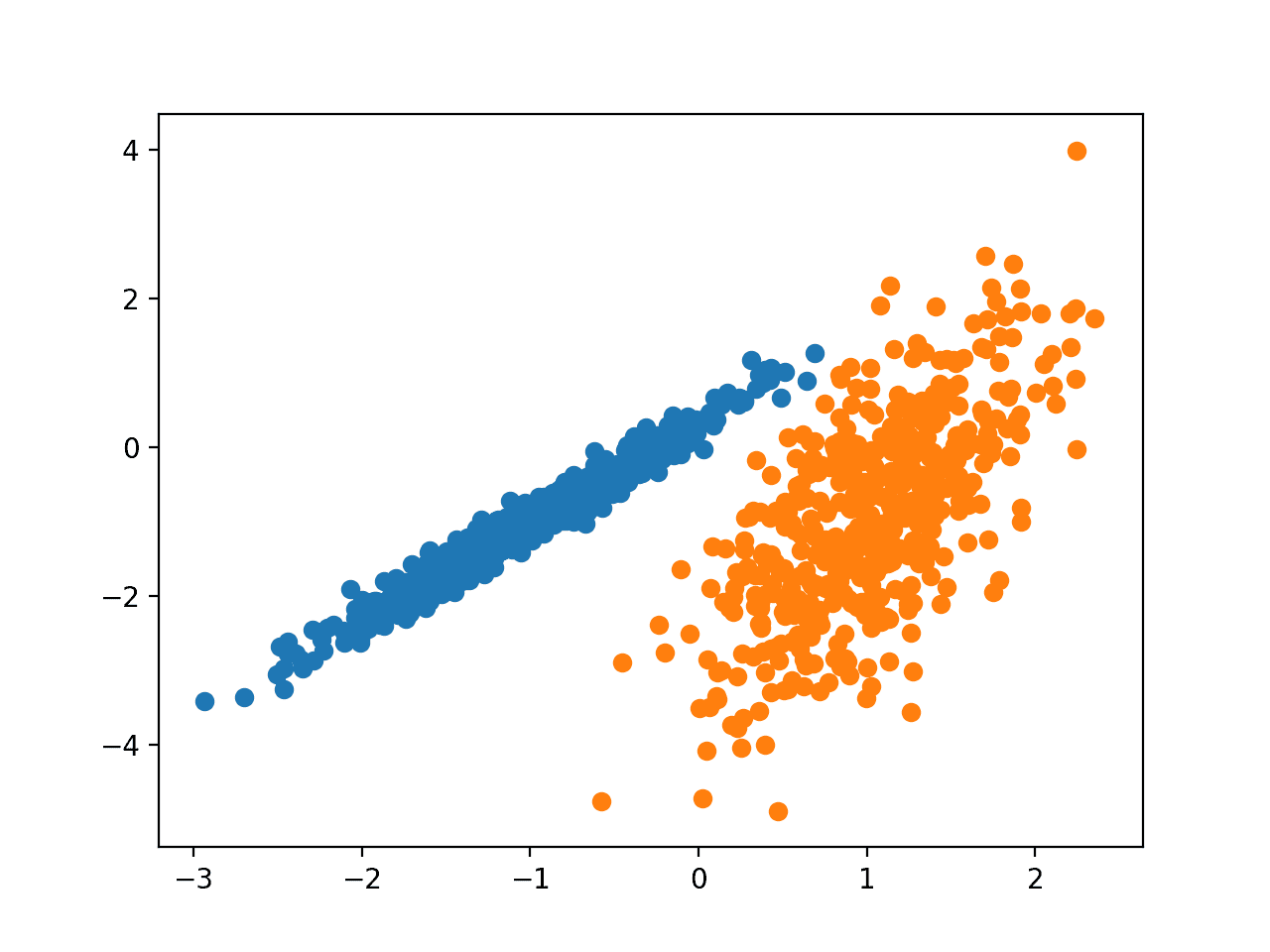
Точечная диаграмма набора данных С Кластерами, Идентифицированными С помощью Кластеризации Гауссовой смеси

Дальнейшее Чтение

В этом разделе содержится больше ресурсов по этой теме, если вы хотите углубиться в нее.

Papers

• Clustering by Passing Messages Between Data Points, 2007.
• BIRCH: An efficient data clustering method for large databases, 1996.
• A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise, 1996.
• Some methods for classification and analysis of multivariate observations, 1967.
• Web-Scale K-Means Clustering, 2010.
• Mean Shift: A robust approach toward feature space analysis, 2002.
• On Spectral Clustering: Analysis and an algorithm, 2002.

Books

• Data Mining: Practical Machine Learning Tools and Techniques, 2016.
• The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2016.
• Machine Learning: A Probabilistic Perspective, 2012.

APIs

• Clustering, scikit-learn API.
• sklearn.datasets.make_classification API.
• sklearn.cluster API.

Articles

• Cluster analysis, Wikipedia.
• Hierarchical clustering, Wikipedia.
• k-means clustering, Wikipedia.
• Mixture model, Wikipedia.

Резюме

В этом уроке вы узнали, как подобрать и использовать лучшие алгоритмы кластеризации в python.

В частности, вы узнали:

Кластеризация-это неконтролируемая проблема поиска естественных групп в пространстве признаков входных данных.
Существует множество различных алгоритмов кластеризации, и нет единого наилучшего метода для всех наборов данных.
Как реализовать, адаптировать и использовать лучшие алгоритмы кластеризации в Python с помощью библиотеки машинного обучения scikit-learn.

Источник: machinelearningmastery.com

Комментарии: