В этой статье я хочу изложить некоторые интересные законы математики, которые пригодятся изучающим Data Science.
Закон Бенфорда
Закон Бенфорда — это математический закон в котором говорится о первой цифре числа из набора реальных данных.
Если мы представим случайное число, то было бы логично предположить, что его первая цифра также будет случайной. То есть вероятность того, что это будет число от 1 до 9, одинакова для каждого из этих чисел, и составляет около 11,1%. Однако это не так.
Закон Бенфорда утверждает, что первая цифра числа чаще будет меньшей, в большинстве реально встречающихся коллекций чисел.
Давайте попробуем применить этот закон к реальному датасету. Для этой статьи я использовал данные из Kaggle о длительности песен в Spotify с 1921 по 2020 год. Вот график того, как часто та или иная цифра является первой:
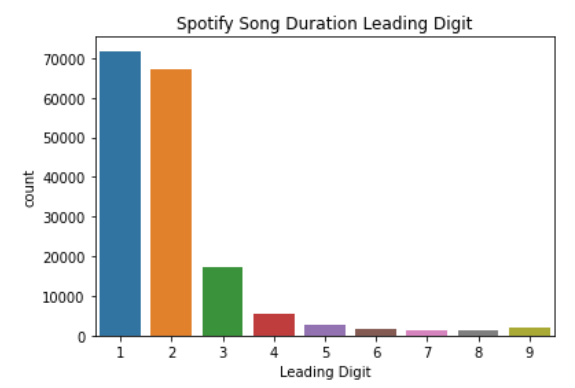
Из данного графика видно, что число 1 встречается чаще всех. И последующие числа плавно уменьшаются в количестве. Это и есть закон Бенфорда.
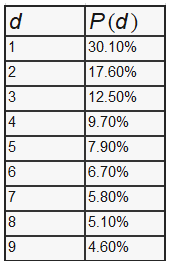
Точное определение закона Бенфорда гласит, что набор чисел подчиняется закону Бенфорда, если первая цифра d (??1,…,9) подходит к этому равенству:

Из этого равенства мы можем получить такое распределение вероятностей:
Существует множество применений этого закона, например для определения махинаций с налогами, результатами выборов, экономическими и бухгалтерскими показателями.
Закон больших чисел
Закон больших чисел гласит, что с возрастанием количества испытаний, средний результат будет стремиться к математическому ожиданию. Этот закон математики является фундаментальным для Data Science.
Например, игральная кость имеет 6 граней со значениями от 1 до 6. Следовательно, среднее значение для него будет 3,5. При броске кости будут выпадать числа от 1 до 6. И чем больше будет число попыток, тем ближе средний результат будет приближаться к 3,5 — это и есть закон больших чисел.
Закон больших чисел отличается от закона средних чисел, который используется для того чтобы описать ожидание того, что результаты случайного события «выровняются» в пределах небольшой выборки. Это называют ошибкой игрока, когда мы рассчитываем на результат близкий к математическому ожиданию, в меньшей выборке.
Закон Зипфа
Закон Зипфа был создан для квантитативной лингвистики. Квантитативная лингвистика это раздел лингвистики, который занимается изучением языка с помощью статистических методов. Закон гласит, что для некоторого набора данных естественного языка, частота любого слова обратно пропорциональна его рангу в таблице частот. Таким образом, наиболее частое слово будет встречаться примерно в два раза чаще, чем второе по частоте, и в четыре раза чаще, чем третье по частоте и так далее.
Например, в предыдущем наборе данных Spotify, я попытался бы разделить все слова и знаки препинания чтобы подсчитать их. Ниже приведены топ-12 наиболее распространенных слов и их частота.
Общее количество слов в данных Spotify составляет 759389. Мы можем проверить применимость закона Зипфа к данному набору данных, посчитав вероятность появления каждого слова. Первым наиболее часто встречающимся словом или пунктуацией является «-», который имеет вероятность ~4%, а затем следует «the», который имеет вероятность ~2%.