XLNet – новейшая и самая крупная модель, появившаяся в активно развивающейся сфере обработки естественного языка (Natural Language Processing, NLP). Статья о XLNet объединяет современные достижения в NLP и инновационный подход к решению задачи языкового моделирования. Обученная на огромном корпусе, модель достигает выдающихся результатов в NLP-задачах бенчмарка GLUE.
XLNet представляет собой авторегрессионную языковую модель, которая выдает на выходе вероятность совместной встречаемости последовательности токенов на основе архитектуры рекуррентного Трансформера. Задачей обучения модели является подсчет вероятности для заданного слова (токена), при условии наличия всех других слов в предложении (а не только слов слева или справа от заданного).
Если вам все понятно в описании выше, то этот пост не для вас. Если же нет, то продолжайте читать о том, как работает XLNet и почему он стал стандартом для многих NLP задач.
Языковое моделирование заключается в подсчете распределения совместной вероятности для последовательности токенов (слов), и зачастую достигается путем факторизации совместного распределения на распределение условной вероятности одного токена с учетом других токенов в последовательности. Например, дана последовательность: "New", "York", "is", "a", "city". Вероятность слова «New» модель подсчитает как , — т.е. вероятность того, что токен "New" находится в той же последовательности, что и токены "is", "a" и "city" (см. рис. 1).
Заметим, что обычно языковая модель принимает текстовую последовательность в токенов, , и подсчитывает вероятность появления некоторых токенов в последовательности при известных : , где and — непересекающиеся подмножества .
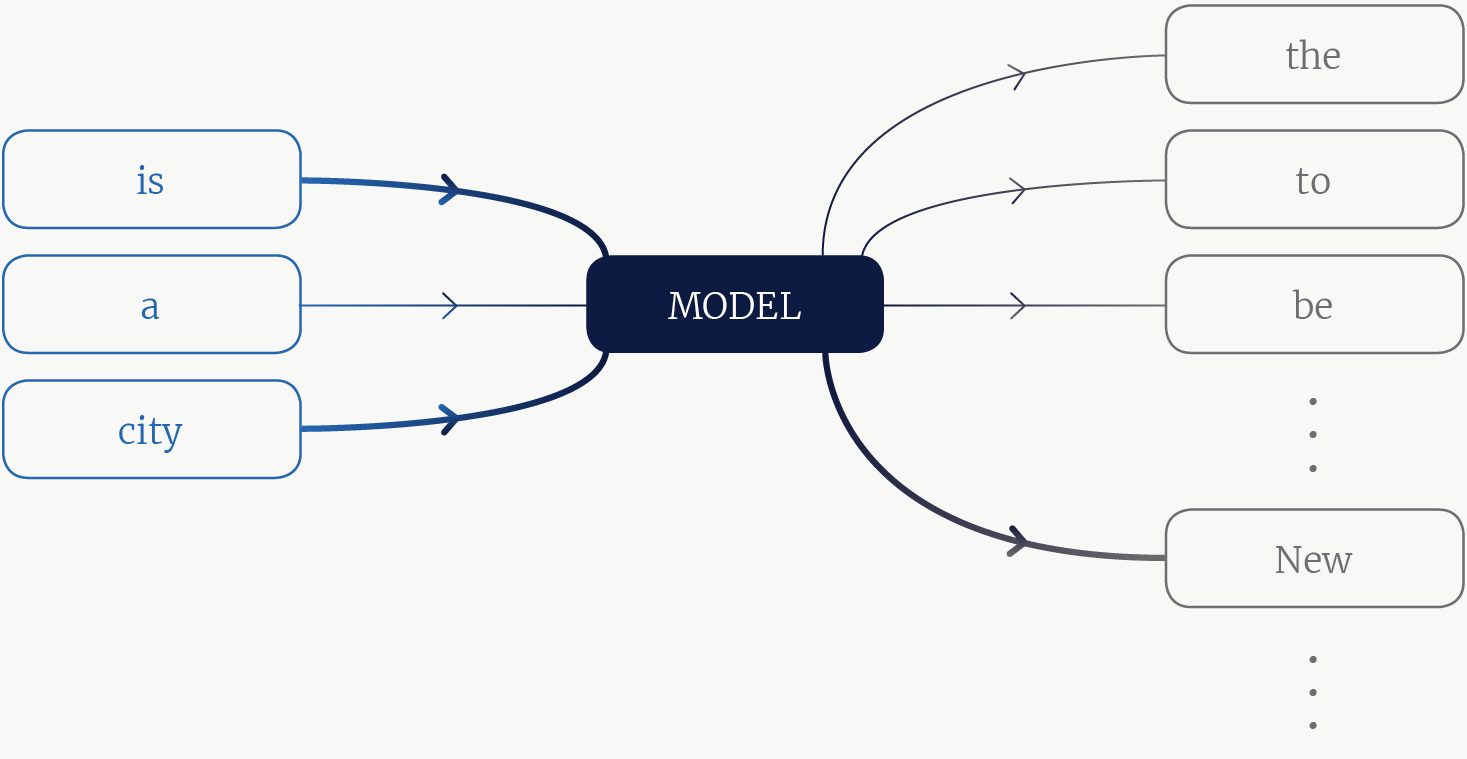
Рис. 1. Языковая модель. Модель – это функция, которая принимает на вход несколько контекстных токенов и выдает на выходе вероятность каждого токена в словаре. Толстыми линиями обозначены более информативные контекстные слова и более вероятные слова из словаря.
Зачем кому-то могла понадобиться модель, которая может подсчитывать вероятность слова в последовательности? На самом деле, особо никому нет до этого дела. Однако модель, содержащая достаточно информации для того, чтобы предсказывать последующие слова в предложении, может быть применена в других более полезных задачах; например, ее можно использовать для определения, кто был упомянут в тексте, какое действие было описано или какую тональность имел текст. Таким образом, с помощью языкового моделирования модели предварительно обучаются и затем тонко настраиваются для решения более практических задач.
Перейдем к основам архитектуры XLNet. Первый компонент языковой модели – это матрица словарных эмбеддингов: каждому токену в словаре присваивается вектор фиксированной длины и, таким образом, последовательность переводится в набор векторов.
Далее нам нужно построить отношения между векторизованными токенами в последовательности. Долгое время признанным фаворитом для решения этой задачи была архитектура LSTM, которая строит отношения между смежными токенами (напр., модель ELMo), однако сейчас наилучшие результаты показывают модели Трансформера (напр., модель BERT). Архитектура Трансформера позволяет объединять несмежные токены, и, таким образом, генерировать более высокоуровневую информацию с помощью механизма внимания. Это помогает модели легче выстраивать более отдаленные отношения в тексте, чем подходы на основе LSTM.
У Трансформеров есть один недостаток: они работают с последовательностями фиксированной длины. Но что, если знание того, что "New" должно появиться в предложении "____ York is a city", также требует, чтобы модель прочитала что-то об Эмпайр-стейт-билдинг в предыдущем предложении? Transformer-XL решает эту проблему, позволяя текущей последовательности видеть информацию из предыдущих последовательностей. Именно на этой архитектуре строится XLNet.
Основной вклад XLNet — это не архитектура, а модифицированная цель обучения языковой модели, которая должна выучить условные распределения для всех перестановок токенов в последовательности. Прежде чем углубиться в детали этой цели, давайте вернемся к модели BERT и объясним такой выбор XLNet.
В бывшей SOTA-модели (BERT) целью обучения было восстановление маскированных слов в предложении: так, для каждого предложения в корпусе некоторые токены заменяются универсальным токеном [mask]. Задача модели — восстановить изначальные токены.
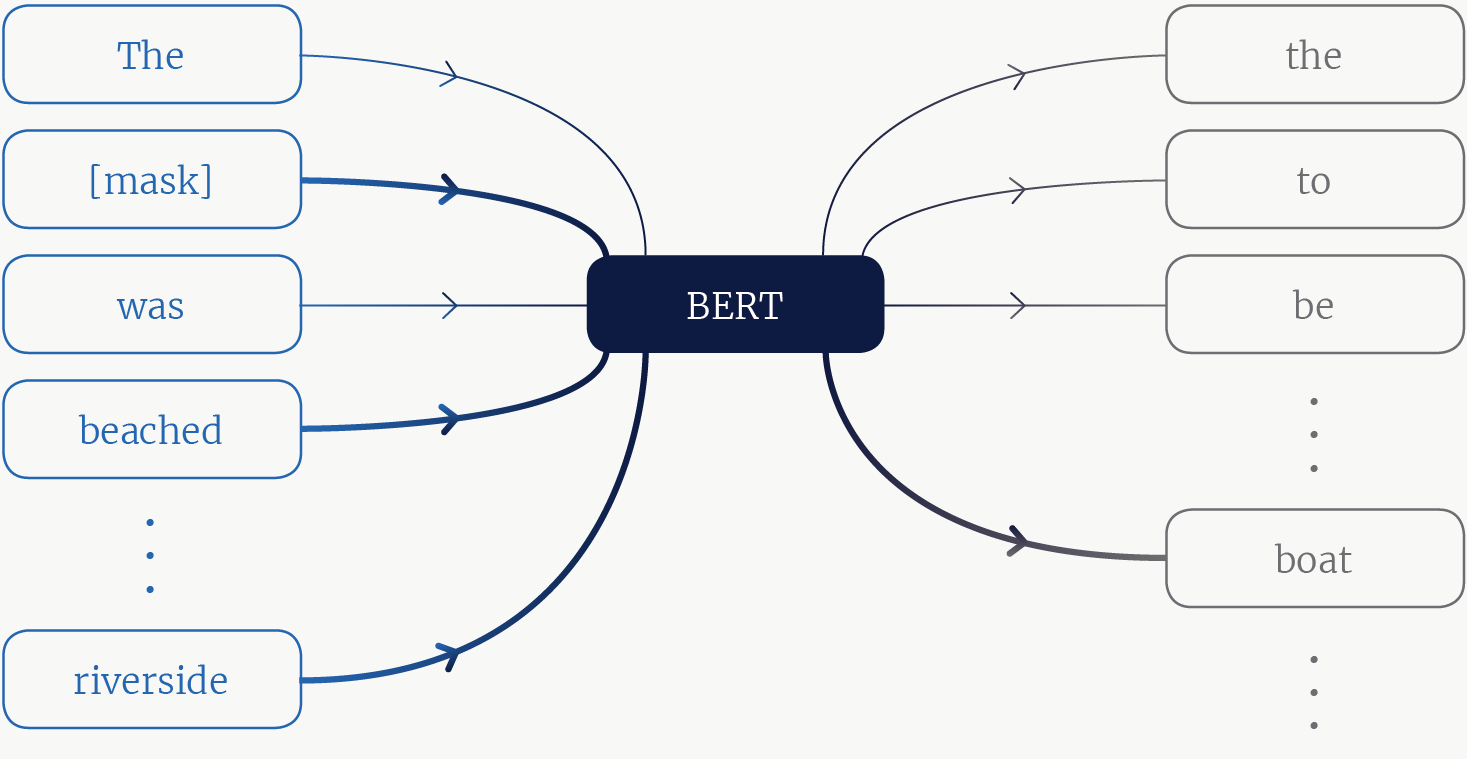
Рис. 2. Изображение модели BERT. На входе модели контекстные токены, некоторые из которых маскированы. Обращая внимание на правильные токены контекста, модель узнает, что наиболее вероятным словом в маскированной позиции будет "boat".
В статье XLNet утверждается, что это не лучший способ обучать модель. Оставим детали аргументации самой статье и вместо этого приведем менее точный, но охватывающий некоторые важные для нас концепции аргумент.
Языковая модель должна кодировать как можно больше информации и нюансов из текста. Модель BERT пытается восстановить маскированные слова в предложении "The [mask] was beached on the riverside" (рисунок 2) ("[mask] была выброшена на берег реки"). Здесь могут встречаться такие слова, как "лодка" или "каноэ". BERT может знать это, потому что лодка может быть выброшена на берег, и ее часто можно найти на берегу реки. Но для BERT'а вовсе необязательно знать это про лодку, достаточно костыля вроде упоминания "берег реки", чтобы сделать вывод, что "лодка" является маскированным токеном.
Более того, BERT предсказывает маскированные токены независимо, поэтому не узнает, как они влияют друг на друга. Если бы пример был "The [mask] was [mask] on the riverside" ("[mask] была [mask] на берег реки"), то BERT мог выдать высокие вероятности не только для таких корректных пар, как ("лодка", "выброшена") и ("парад", "виднелся"), но и для пары ("парад", "выброшен").
Такие подходы, как BERT и ELMo, стали в свое время SOTA за счет включения в предсказание левого и правого контекстов. XLNet пошла еще дальше: модель предназначена для предсказания каждого слова в последовательности, используя любую комбинацию других слов в этой последовательности. XLNet могут попросить предсказать, какое слово может следовать за "The" в нашем предложении. Вероятно, много слов, но "лодка" более вероятна, чем "они", потому что модель уже кое-что узнала о лодке (в основном, что это не местоимение). Затем модель могут попросить предсказать второе слово, учитывая, что последующие слова — "была" и "выброшена". И затем ее могут попросить предсказать четвертое слово, учитывая, что третье "был", пятое "на" и седьмое — "берег реки.
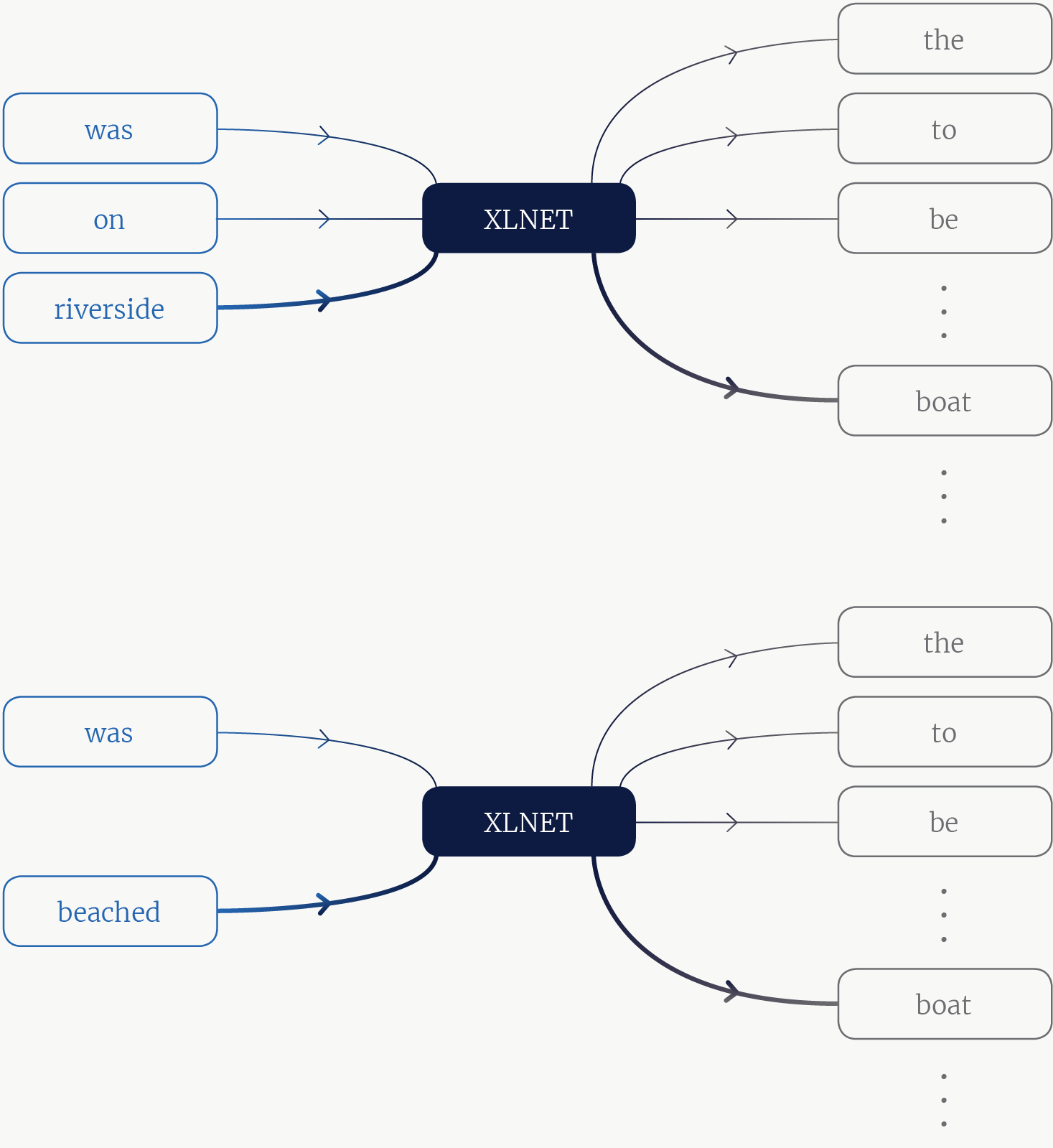
Рис. 3. Изображение модели XLNet. Задача — рассчитать, что лодка является вероятным токеном для многих различных контекстов, взятых из последовательности.
Таким образом, XLNet действительно не на что опереться. Ей подают сложный и зачастую неоднозначный контекст, из которого необходимо определить, входит ли слово в предложение. И это то, что позволяет модели выжать больше информации из обучающего корпуса (см. рис. 3).
На практике модель XLNet делает выборку из всех возможных перестановок, так что ей не удается просмотреть каждое отдельное отношение. Также, она не использует очень маленькие контексты, поскольку они мешают обучению. После применения этих практических эвристик XLNet стала больше походить на BERT.
В следующих нескольких разделах будут рассмотрены более сложные аспекты статьи.
Для последовательности авторегрессионная (auto-regressive, AR) модель
подсчитывает вероятность . В языковом моделировании, это вероятность токена в предложении при условии, что токены предшествуют ему. Эти обуславливающие слова называют контекстом. Подобная модель ассиметрична и не получает информацию о всех отношениях между токенами в корпусе.
Авторегрессионные модели, такие как ELMo, позволяют также учиться отношениям между токеном и последующими токенами. Цель AR в этом случае может рассматриваться как . Это авторегрессия для обратной последовательности. Но зачем останавливаться? Ведь могут существовать отношения, интересные для задачи обучения, как между двумя ближайшими токенами , так и вообще для любой комбинации токенов .
XLNet предлагает в качестве цели обучения получить представление над всеми такими перестановками. Возьмем, например, последовательность , где . Получится набор из всех 4! перестановок . Модель XLNet авторегрессионна для всех таких перестановок: она может посчитать вероятность токена , учитывая предыдущие токены для любого порядка из .
Например, можно вычислить вероятность третьего элемента с учетом двух предыдущих из любой перестановки. Три перестановки , и будут соответствовать , и . Схожим образом вероятность второго элемента с учетом первого можно выразить как , и . Если же рассматривать все 4 позиции и все 4! перестановок, то модель будет учитывать все возможные зависимости.
Эти идеи включены в следующую формулу из статьи:
Описанный критерий ищет параметры модели , обеспечивающие максимальную вероятность токенов в последовательности длиной с учетом предыдущих токенов , где – это элемент перестановки индексов токенов и – предыдущие элементы перестановки. Сумма логарифмов вероятностей означает, что для любой одной перестановки модель авторегрессионна, поскольку она является произведением вероятности для каждого элемента в последовательности. Ожидается, что по всем перестановкам в модель будет обучена одинаково вычислять вероятности для любого токена в любом контексте.
Но в текущем представлении модели чего-то не хватает: откуда она знает о порядке слов? Модель может вычислить , а также . В идеале она должна кое-что знать об относительном положении "This" и "is", а также "a". В противном случае модель просто бы решила, что все токены в последовательности с равной вероятностью находятся рядом друг с другом. Нам нужна модель, которая предсказывает
и , а для этого она должна знать индексы токенов контекста.
Архитектура Трансформера решает эту проблему, добавляя позиционную информацию в эмбеддинги токенов. Цель обучения можно представить как . Но в случае, если токены предложений действительно будут перемешаны, подобный механизм сломается. И здесь на помощь приходят маски внимания. Когда модель вычисляет контекст, который является входом для вычисления вероятности, она всегда использует один и тот же порядок токенов и просто маскирует те токены, которые не находятся в рассматриваемом контексте (т.е. те, которые поступают впоследствии в перемешанном порядке).
В качестве конкретного примера рассмотрим перестановку . При вычислении вероятности первого элемента в этом порядке (т.е. токена 3) модель не имеет контекста, поскольку другие токены еще не были поданы. Таким образом, маска будет . Для второго элемента (токен 2) маска равна , поскольку его единственный контекст — это токен 3. Следуя этой логике, третий и четвертый элементы (токены 4 и 1) имеют маски и . Сложив все элементы в порядке токенов, получится матрица (как показано на рис. 2 статьи):
Можно также посмотреть на это с другой стороны: цель обучения будет содержать следующие условия, где подчеркивания представляют маскированные токены:
Остается исправить одну ошибку: мы хотим, чтобы вероятность не только зависела от индексов токенов контекста, но и от индекса токена, вероятность которого вычисляется. Другими словами мы хотим вычислить : вероятность "This" при условии, что это первый токен, а "is" — второй. Но архитектура Трансформера кодирует позиционную информацию 1 и 2 внутри эмбеддинга для "This" и "is". Значит это должно выглядеть как . К сожалению, модель теперь просто напросто знает, что токен "This" должен быть вероятен как часть предложения.
Решение этой проблемы — двухпотоковый механизм внутреннего внимания. Каждая позиция токена имеет два связанных вектора на каждом слое внутреннего внимания : and . Векторы принадлежат потоку содержания (content stream), а векторы – потоку запроса (query stream). Векторы потока содержания инициализируются эмбеддингами токенов, добавленными к позиционным эмбеддингам. Векторы потока запросов инициализируются общим вектором эмбеддинга , добавленного к позиционным эмбеддингам. Стоит отметить, что вектор будет одним и тем же независимо от токена, и поэтому не может использоваться для различения токенов.
На каждом слое каждый вектор содержания обновляется с использованием тех векторов , которые остаются немаскированными, и самим собой (эквивалентно демаскированию диагонали из матрицы, показанной в предыдущем разделе). Таким образом, обновляется маской , а вектор обновляется маской . Обновление использует векторы содержания в качестве запроса, ключа и значения.
Каждый вектор запроса , напротив, на каждом уровне обновляется с использованием немаскированных векторов содержания и самого себя. Обновление использует в качестве запроса, а вектор в качестве ключей и значений, где — индекс немаскированного токена в контексте .
На рисунке 4 показано, как подчитывается запрос для 4-го токена в -ом слое внутреннего внимания. Это показывает, что представляет собой совокупность "is + 2", "a + 3" и позиции 4, что в точности соответствует контексту, необходимому для вычисления вероятности токена "sentence".
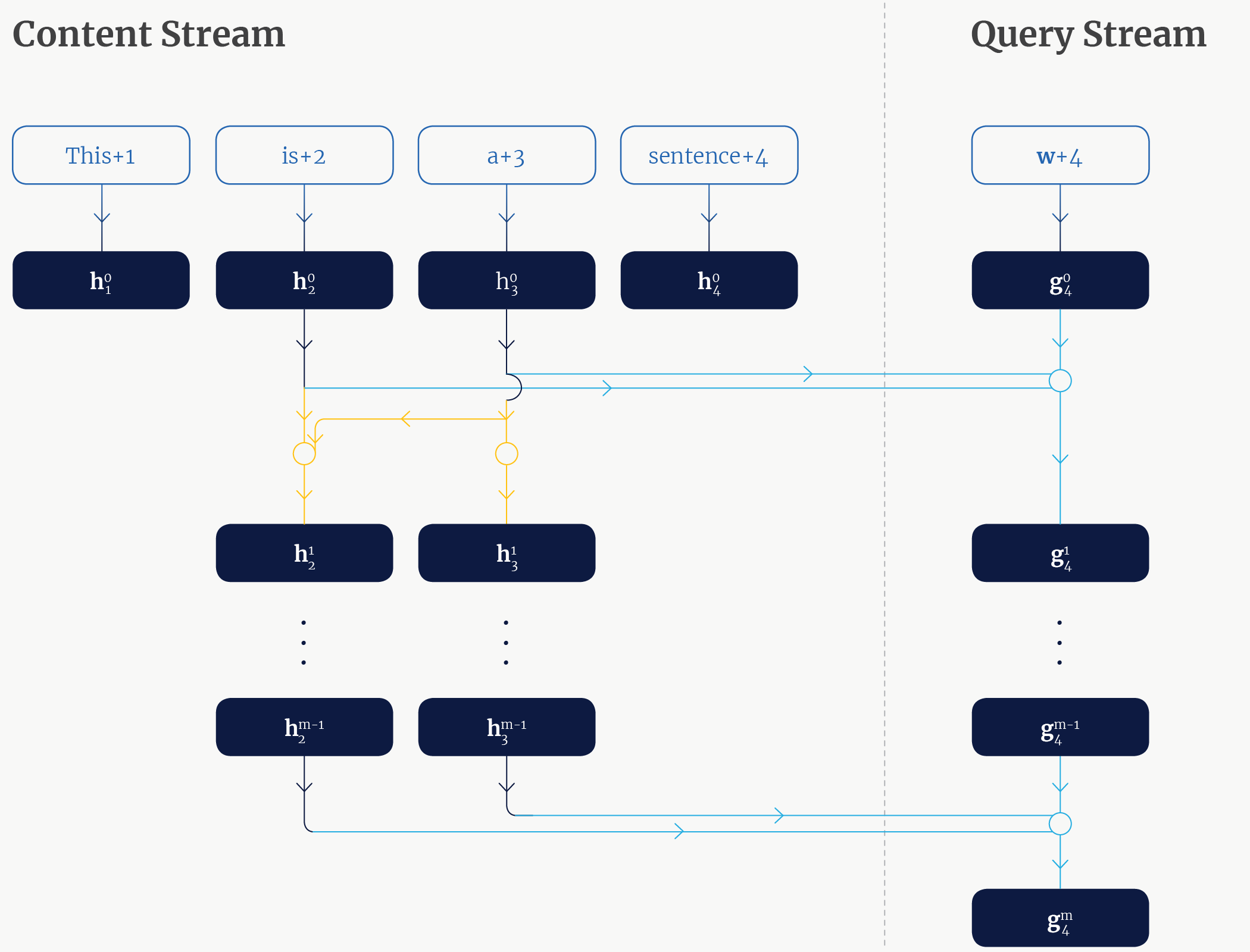
Рис. 4. Двойной механизм внимания для подсчета – четвертого токена в -ом слое внутреннего внимания. Стрелки указывают на передачу информацию от векторов. Пересечения линий и кругов указывают на подсчет и агрегацию операций запроса/ключа/значения механизма внутреннего внимания. Желтые линии обозначают обновления потока содержания для третьего символа (зависит только от себя самого) и второго символа (зависит от себя и от третьего символа). Голубые линии обозначают обновление потока запроса (зависит от себя, второго и третьего символа из потока содержания).
В продолжение предыдущей секции, цель обучения может быть сформулирована следующим образом, где обозначает позицию токена, для которого подсчитывается вероятность:
Работает ли все это? Краткий ответ — да. Длинный ответ — тоже да. Возможно, это не так уж и удивительно: XLNet опирается на предшествующие современные методы. Она была обучена на корпусе из 30 миллиардов слов (на порядок больше, чем тот, который использовался для обучения BERT'а, и был взят из более разнообразных источников), и это обучение потребовало значительно больше часов вычислительного времени, чем предыдущие модели:
| Модель | Объем вычислений |
|---|---|
| ULMFit | 1 GPU-день |
| ELMo | 40 GPU-дней |
| BERT | 450 GPU-дней |
| XLNet | 2000 GPU-дней |
Таблица 1. Приблизительное время вычислений для обучения актуальных моделей NLP.
Вероятно, более интересно, что исследование абляции XLNet показывает: XLNet работает лучше, чем BERT при честном сравнении (рис. 5). То есть когда модель обучается на том же корпусе, что и BERT, с использованием тех же гиперпараметров и того же количества слоев, она неизменно превосходит BERT. Что еще более интересно, XLNet также превосходит Transformer-XL в честном сравнении. Transformer-XL можно рассматривать как отказ от цели перестановки AR. Постоянное улучшение данного показателя свидетельствует об эффективности этого метода.
Результаты абляции
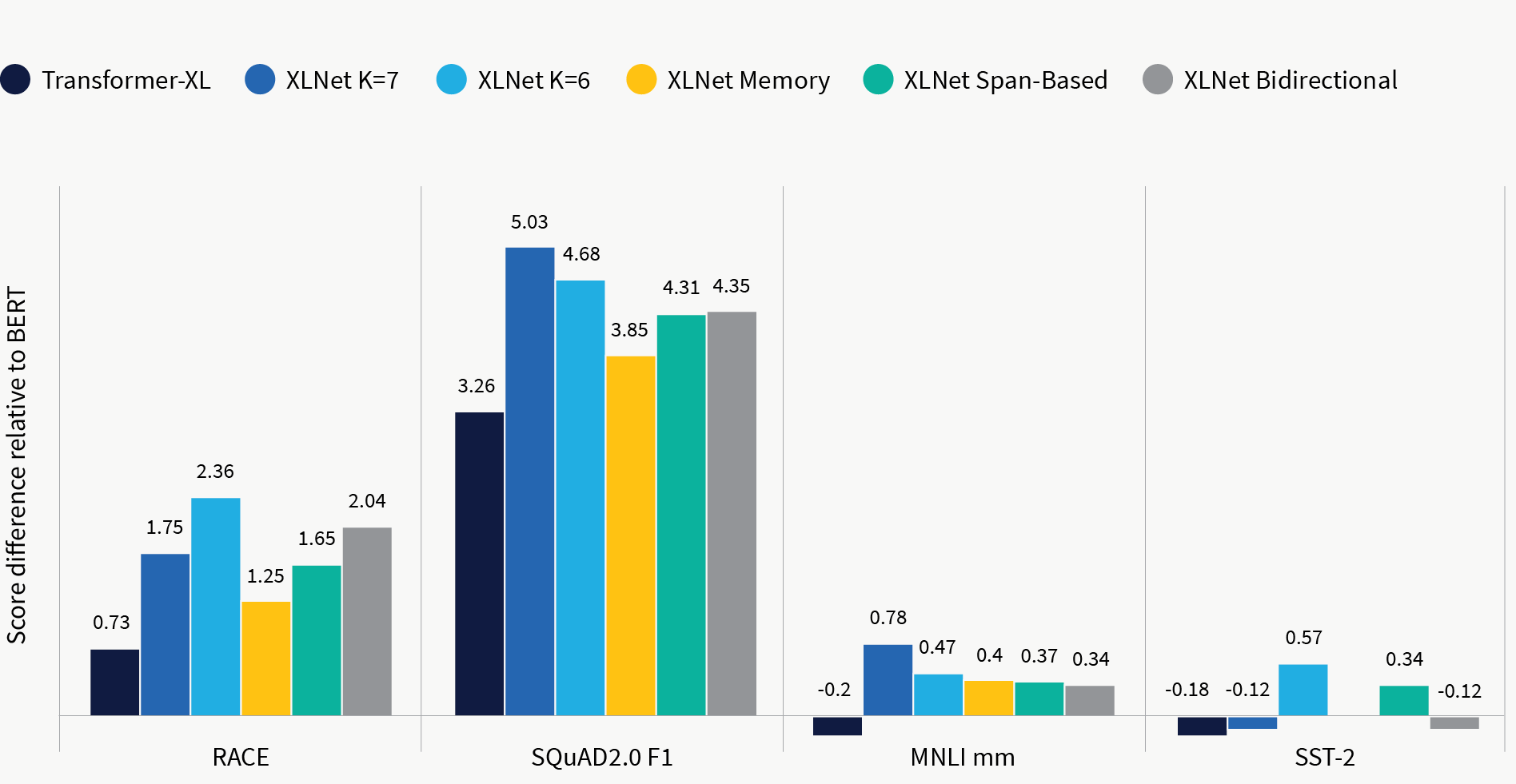
Рис. 5. Исследование абляции XLNet на четырех бенчмарках: RACE, SQuAD2.0 F1, MNLI mm и SST-2. Результаты сходны с результатами BERT на одном обучающем датасете. Различные столбцы представляют различные настройки обучения, описанные в части 3.7 статьи.
Что не может оценить исследование абляции, так это вклад двухпотокового механизма внутреннего внимания в улучшение производительности XLNet. Последний позволяет механизму внимания явно учитывать позицию целевого токена и вводить дополнительную скрытую емкость в виде векторов потока запросов. Хотя это довольно сложная часть архитектуры XLNet, вполне возможно, что такие модели, как BERT, также могут извлечь выгоду из этого механизма без использования той же цели обучения, что и XLNet.
- Авторы оригинала — G. McGoldrick, Y. Cao, S. Prince
- Перевод — Смирнова Екатерина
- Редактирование и вёрстка — Шкарин Сергей