Кластерный анализ и дилемма биологического пользователя
МЕНЮ
Главная страница
Поиск
Регистрация на сайте
Помощь проекту
Архив новостей
ТЕМЫ
Новости ИИ
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Искусственный интеллект
Слежка за людьми
Угроза ИИ
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Нейронные сети начинающим
Психология ИИ
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Творчество ИИ
Техническое зрение
Чат-боты
Авторизация
2021-01-14 19:48
машинное обучение новости, Теория эволюции, кластеризация данных
Век информации
В ХХI веке и на работе, и в быту нас окружают все б?льшие и все более сложно устроенные данные. Причина — развитие новых технологий получения и хранения информации, включая цифровые изображения, социальные сети и интернет. Такого рода данные принято обозначать как Большие (big data) — ответственность за них взяла на себя самобытная наука о данных (data science), которая создает новые методы анализа и визуализации. Отметим — удивительно сблизившиеся в этом случае! Закономерно: ведь обработка подобной информации привычными статистическими инструментами затруднена или даже невозможна (рис. 1).
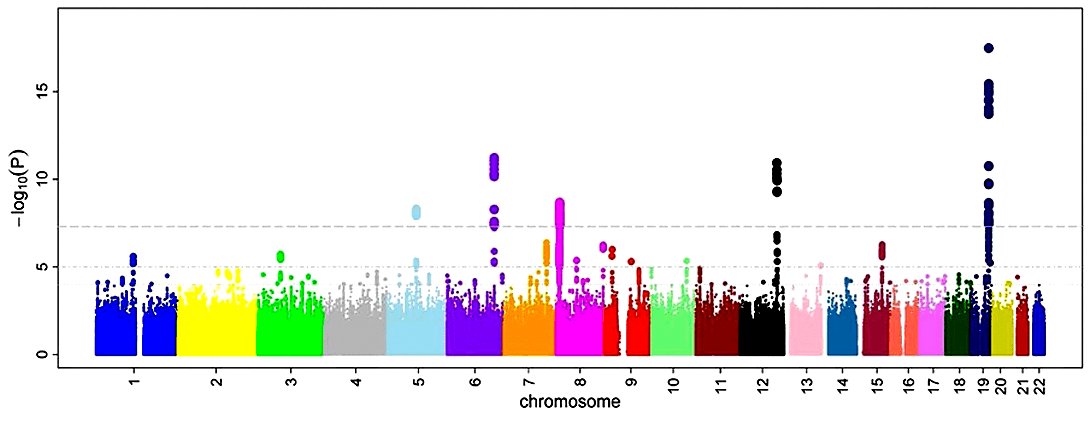
Рисунок 1. Манхэттенский график — результат GWAS. Пример больших и геномных данных — полногеномный поиск ассоциаций (англ. genome-wide association studies, GWAS). Иллюстрирующие GWAS так называемые манхэттенские графики сейчас пестрят на страницах биомедицинских изданий. На них по оси X отмечают положение однонуклеотидных полиморфизмов SNP (располагая их от «начала» первой хромосомы и до конца 22-й — половые не в счет), а по оси Y — уровень ассоциации данного SNP и некоторого фенотипа. Пики на таком графике указывают на целевые хромосомные координаты. Несмотря на информативность, от обилия точек пестрит в глазах — а ведь за каждой из них стоит увесистая статистика и множество испытуемых.
Ко всему прочему, данные могут оказаться не только непомерно объемными (скажем, очень «высокие» таблицы с тысячами наблюдений), но и многомерными — то есть содержать информацию сразу о множестве признаков описываемых объектов. Признаки, в свою очередь, грозят оказаться разнородными — качественными, количественными, с пропущенными значениями... И если мы хотим для наглядности изобразить наши данные, то три показателя некоторого наблюдения придется сопоставить точке в трехмерном пространстве. N параметров приведут нас уже в N-мерное пространство... N при этом, по своему обыкновению, стремится к бесконечности, а логика и способность ориентироваться, присущие трехмерному человеку, стремительно теряют смысл.
Однако вернемся из гиперпространства в рабочие будни. Как изменилась информация, которую используют ученые, в частности, в естественных науках? Примеров стремительно «раздавшихся» в своих размерах и размерности данных в науке можно привести множество. Самые примечательные — это, пожалуй, спутниковые снимки («виновники» огромного прогресса в географии и других науках о Земле), а также данные высокопроизводительного секвенирования нуклеиновых кислот (next generation sequencing, NGS) [3], которые на слуху у каждого современного биолога.В «сухом» остатке
Методы получения последовательностей ДНК (особенно новые, по-настоящему эффективные NGS) преобразили современные науки о живом и сделали возможным новый «обзорный» подход к исследованию геномов — геномику. Напомним, что объектами исследования геномики являются целые геномы, рассматриваемые в различных аспектах (структурном, функциональном, эволюционном...) Иными словами, геномика, в отличие от рассматривающей индивидуальные гены генетики, исследует сразу всю их взаимодействующую совокупность.
За геномикой следом возникли младшие сестры «омискного семейства» — протеомика, метаболомика, липидомика, гликомика и другие [4]. Каждая из этих научных отраслей ставит своей целью описать сразу все молекулы некоторого определенного сорта — белки, малые молекулы-метаболиты, липиды и прочие жиры, а также углеводы, соответственно [4]. Подход омик — обобщающий и системный — обращается к очень обширным данным о множестве объектов, рассматривая также связи между ними. Оказались необходимы методы обработки Больших данных (big data), которые к тому времени подоспевали из других наук.
Обратимся теперь к самому насущному в постгеномную эру [5] примеру больших и при этом биологических данных. Нетрудно догадаться, что речь идет о сиквенсах (англ. sequence) — последовательностях ДНК, РНК и белков. С точки зрения анализа данных и информатики это объекты типа «строка» (англ. string). Строки — это некоторая последовательность букв из заданной совокупности, называемой алфавитом. Информатика и примкнувшая к ней биоинформатика создали обширный инструментарий для объектов такого типа. В итоге мы можем:
- рассчитать для некоторого фрагмента ДНК встречаемость отдельных нуклеотидов (скажем, долю А, GC-состав, соотношение числа всех возможных ди-, три-, тетра- и так далее нуклеотидов);
- отыскать положение особых «слов» в «тексте» ДНК, в том числе заданных не строго, а также описать с помощью логотипов последовательности;
- вычислять различные параметры этой молекулы «скользящим окном»;
и многое другое.
Интересный и очень важный пример — расчет текстового расстояния, то есть меры сходства последовательностей. В самом простом случае это p-расстояние, равное числу замен, которые необходимо внести в одну последовательность для ее превращения в другую . Что-то вроде игры-задачки про переделывание «мухи» в «слона», только с другими правилами. Вычисление текстовых расстояний позволяет оценить время эволюционного расхождения для некоторых последовательностей — стало быть, и их родство. Условно говоря, текстовое расстояние нарастает с ходом молекулярных часов [6]. Различные текстовые меры сходства активно используются молекулярной филогенетикой для построения эволюционных деревьев — в комплекте с опять-таки кластеризацией, а именно методами иерархического кластерного анализа.
Некоторые биоинформатические алгоритмы были разобраны в статье «12 методов в картинках: “сухая” биология» [7].
В случае биострок мы имеем последовательности «биологических букв» — по 4 для двух нуклеиновых кислот (ДНК и РНК) с лишь одной различающейся (T и U, соответственно) и тремя общими (A, C, G) в их словарях. В случае белков «алфавит» насчитывает двадцать букв-аминокислот (с неизбежной оговоркой «иногда чуть больше» [8]). Секвенирование белков — реализованная задача, которая, однако, остается экзотикой. А вот в случае нуклеиновых кислот (прежде всего ДНК) результаты получены поистине прорывные! Благодаря NGS за пару десятилетий скорость получения нуклеотидных последовательностей возросла на многие порядки, в то время как стоимость пропорционально уменьшилась [9].
К сожалению, на фоне такого оглушительного успеха «мокрой» биологии возникают затруднения «сухого», то есть биоинформатического характера. Проблема особенно актуальна в случае новых геномов и метагеномов (своеобразных «несортированных геномных отвалов»). Речь идет прежде всего об аннотировании ДНК — поиске участков различного типа (кодирующих, регуляторных, повторов [10] и др.) и их привязке к определенным хромосомным координатам. Незаменимую помощь биологам в этом оказывают как раз методы машинного обучения (machine learning).
Роботы тоже учатся
Машинное обучение представляет собой автоматическую обработку данных: методы сближают его с областью математической статистики. Той самой областью, которая нередко скорее пугает, нежели привлекает биологов, и которая населена медианами, Стьюдентом с его t-критерием, пестрящими интегралами распределениями и ящиками с усами. От других инструментов статистики и анализа данных машинное обучение отличает то, что оно рассматривает некоторую проблему не напрямую, а в ходе обучения — при решении множества сходных задач. Соответствующий англоязычный термин — machine learning, или, общеупотребительно кратко, ML. Идея в основе машинного обучения отнюдь не нова: та же линейная регрессия, призванная предсказать простую зависимость одной переменной от другой или других, формально представляет собой ML. Данный пример, безусловно, примитивный: регрессия — это очень древний (хотя и ходовой) представитель разнообразия machine learning.
В целом динамичное и развивающееся вполне эволюционно разнообразие методов и алгоритмов ML естественно сравнивать с биоразнообразием — продуктом эволюции в полном и прямом смысле. Если задаться такой систематикой in silico, то прежде всего стоит выделить следующие группы машинного обучения:
- Машинное обучение с учителем (supervised machine learning). Сюда относится ML в узком смысле — иногда это понятие относят только к этой подгруппе. В этом случае часть наблюдений имеет определенные заданные исходы («ярлыки», «лейблы» и пр.) — то eсть известно об их принадлежности к определенной категории или группе. Скажем, когда для некоторой части исследуемых клеток заведомо установлена принадлежность к опухоли или даже опухоли определенного типа. Результатом работы таких алгоритмов является: a) предсказание групповой принадлежности остальных объектов — в случае классификации; либо б) некоторые количественные значения для них (например, продолжительность жизни с момента постановки диагноза) — если мы имеем дело с регрессией.
- Машинное обучение без учителя (unsupervised machine learning) — большая группа довольно разнородных методов, среди которых и интересующий нас кластерный анализ. Сюда относятся, во-первых, различные методы понижения размерности (призванные уменьшить пресловутое N, переводя данные в область более «человекочитаемых» измерений). Самыми заметными представителями являются метод главных компонент (principal component analysis, PCA) и, скажем, набирающий популярность в биологической среде метод со звучным названием t-SNE (t-stochastic neighbor embedding, t-стохастическое внедрение соседей). Другой пример «предоставленного самому себе» (буквальный перевод unsupervised) ML — это как раз кластеризация (или кластерный анализ). И если методы понижения размерности проецируют многомерное облако данных в двумерную (например) «тень», то кластеризация выделяет структуру данных непосредственно в N-мерии — и рапортует нам об успехах. Образовалась и «помесь» методов снижения размерности и кластеризации: спектральная кластеризация сначала понижает размерность данных и уже далее кластеризует.
- Обучение с частичным привлечением учителя — довольно неуклюжий перевод английского semi-supervised machine learning. Методы этой группы используют входные данные с заданной групповой принадлежностью (подобно методам с «полным привлечением учителя»). Однако они не гнушаются и неразмеченными данными (без «лейбла»), чем напоминают уже кластеризацию. Такие методы возникли как закономерное следствие скрещивания первых групп и сочетают их сильные стороны. Примером служит ограниченная кластеризация (constrained clustering). В этом случае для ряда наблюдений заданы попарные связи в формате «обязательно положить в один кластер» (must-link) и «эти двое точно не в одном кластере» (cannot-link) [11–13].
Теперь обратимся к более дробной систематике — основным разновидностям собственно кластерного анализа. Две наиболее очевидные группы — это плоские и иерархические методы. Кластерный анализ — вещь, которая понятнее всего на практике. Его стоит «покрутить в руках» для настоящей наглядности. Поэтому мы рассмотрим работу ключевых алгоритмов на одних данных (простых и, в то же время, биологических). Используем для этого очень подходящий для всяческого анализа биологических данных язык R.
Среди прилагающихся к R наборов данных есть датасет «хищные» (carnivora). Из него мы возьмем данные о 43 хищных представителях семи семейств — а именно такие их характеристики, как:- масса тела самки (для определенности);
- средний вес животных (и самок, и самцов);
- вес мозга самки;
- средний вес мозга животных обоих полов;
- среднее число рожденных детенышей;
- продолжительность беременности;
- вес при рождении;
- длительность грудного вскармливания.
Здесь стоит предостеречь читателя. Кластерный анализ этого небольшого набора показателей морфологии и воспроизводства не следует считать анализом их эволюционного родства. В этой связи систематику живого он в большинстве случае не воспроизводит. Зато позволяет выделить осмысленные группировки, основанные на габаритах тела и образе жизни. Если мы захотим увидеть привычные биологу филогенетические деревья (дендрограммы, служащие отражением эволюционного прошлого и таксономического настоящего данных видов), то нам следует прибегнуть к молекулярной филогенетике [14]. Это важнейший инструмент современной биоинформатики и биологии в целом. Мы уже упоминали текстовые расстояния — как с их помощью измерять степень родства последовательностей ДНК. Так вот, задача реконструкции эволюционного процесса сводится к оценке родства на основе одной из моделей молекулярной эволюции и последующем построении опять-таки иерархической кластеризации. Прекрасный пример того, как кластеризация невзначай вросла в биологический инструментарий...
Вернемся же к нашему «несистематическому» группированию хищников.
Для начала вооружимся плоскими алгоритмами кластеризации (также вероятностные, англ. partitional). Такие подходы и попроще, и побыстрее в расчетах. Их задача — разложить имеющиеся наблюдения по заданному нами количеству кластеров. Происходит такой анализ «одним махом» — за один шаг, однако шаг этот можно повторять много раз для улучшения получаемого результата. Итак, начнем с алгоритма k-средних (k-means) как прародителя и самого ходового представителя плоских алгоритмов. Задача k-means — распределить все предложенные объекты на k кластеров, причем бремя определения k ложится на нас самих [13], [15].
Предварительно нормируем данные, чтобы сотни граммов, в которых изменяется масса мозга, не заглушили собой считанные единицы потомства. Сам анализ проведем на всех восьми переменных, а для визуализации выберем в качестве осей пару делающих изображение наиболее наглядным (а именно массу мозга самки и продолжительность беременности). Зная наперед «верный ответ» — а именно что наши животные представляют семь семейств, — установим k = 7 и сравним результаты с этим корректным с позиций систематики разбиением (рис. 2).
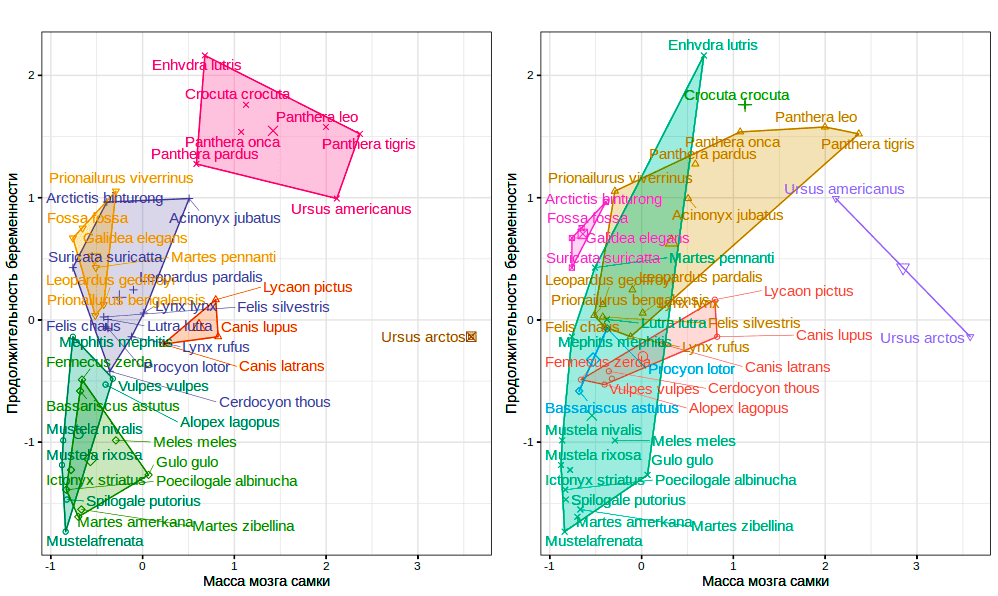
Рисунок 2. Данные carnivora: результаты кластерного анализа k-средних для семи кластеров (слева) и принадлежность рассмотренных животных к реальным семействам (справа). Цветами обозначены кластеры и семейства, соответственно.
В результате мы видим, что этот плоский алгоритм не очень-то хорошо воспроизводит систематические взаимоотношения животных... Но мы условились, что ждем от него другого — группировки главным образом по размерам. Действительно, кластеризация объединила в одном кластере крупных кошек (Panthera sp.) и таких крупных «некошачьих» хищников, как гиену (Crocuta crocuta), калана (Enhydra lutris) и даже умеренного по своим размерам медведя — черного американского (Ursus americanus). Представленное многочисленными видами и разношерстное семейство куньих ожидаемо оказалось разбитым на несколько кластеров, а, скажем, самый крупный бурый медведь (Ursus arctos) попал в собственный «одноместный» кластер.
Переключимся на иерархические алгоритмы кластеризации на примере метода Уорда (Ward). Статистики и математики (для которых кластеризация — это не только инструмент, но и объект исследования) также называют такие алгоритмы таксономиями, подчеркивая сходство с «деревьями жизни». Здесь развитие статистики и машинного обучения напрямую вдохновлялось таксономией органического мира — классической систематикой с иерархией таксонов, предложенной такими мэтрами биологии, как К. Линней и О. Декандоль в XVIII веке. Вдохновение — это хорошо, но возникает непростой момент, когда «таксономия» биологов соприкасается с «таксономией» из области машинного обучения... А «классификация» у биологов так похожа на «таксономию» у биологов, притом что ML их противопоставляет (первая — обучение с учителем, вторая — без...). Что ж, остается учиться оперативно переключаться!Иерархические методы предполагают не одно разбиение имеющихся наблюдений «с плеча», а целую иерархию последовательных разбиений. Их очень удобно изображать в виде дендрограмм (деревьев), из которых биологу чаще всего приходится иметь дело с эволюционными деревьями (дендрограммы, изображающие филогенез — то есть эволюцию). Иерархическая кластеризация в сравнении с плоской будет и попроще, и посложнее. Попроще потому, что не требует задавать число кластеров изначально. Более того, есть шанс обойтись без привлечения «сторонних» способов оценить заветное k — при взгляде на уже полученную дендрограмму мы можем его прикинуть. Посложнее придется компьютеру — ему потребуются большие вычислительные возможности для построения иерархической кластеризации в сравнении с плоской. Среди иерархических алгоритмов выделяют две группы. Более распространены так называемые агломеративные (agglomerative) алгоритмы, которые собирают иерархическое дерево «снизу вверх». Они начинают свою работу с «одноместных» кластеров с отдельными объектами. Дивизивные (divisive) подходы поступают наоборот, а именно «сверху вниз». Сначала они помещают все наблюдения в один кластер и далее последовательно разбивают его на всё более мелкие.
На нашем «хищном» датасете мы применим агломеративный иерархический метод — метод Уорда (Ward) (рис. 4). Для получаемых с его помощью кластеров характерна компактность, «сжатость» — поскольку алгоритм стремится минимизировать их статистическую дисперсию [15].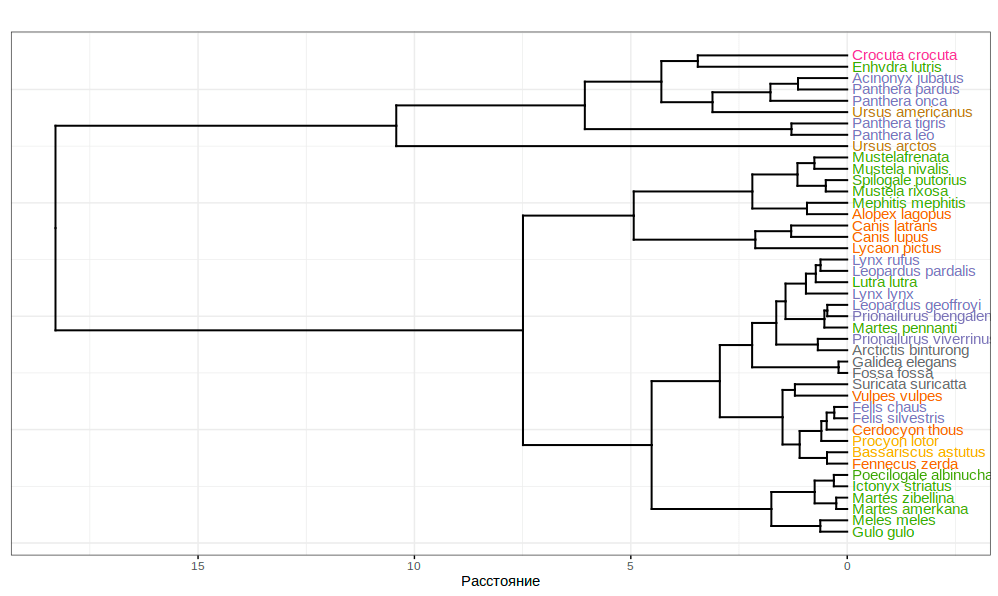
Рисунок 4. Иерархическая кластеризация датасета carnivora. Семейства обозначены цветами. Важно подчеркнуть — дендрограмма перед нами не является эволюционным древом! Эволюционные деревья (кладограммы и филограммы) также строят с применением иерархической кластеризации, но уже на основе данных моделей молекулярной филогенетики.
Получившийся рисунок радует биологический глаз: на первый взгляд он очень похож на эволюционное дерево. Однако в его основе — расстояние по всего нескольким параметрам морфологии и образа жизни, а не применяемое обычно для построение настоящих филограмм текстовое расстояние между фрагментами ДНК. Так что перед нами — просто дендрограмма кластеризации отдельных признаков. Что, впрочем, на помешало ей вполне успешно объединить ряд родственных видов.
«Кластер — в глазах смотрящего»
Теперь разберемся с базовыми понятиями в области кластерного анализа. А также с тем, почему с ними не всегда все понятно. Итак, термин кластерный анализ объединяет в себе множество статистических методов. Их общая задача — выявление естественной группировки (либо группировок) для некоторой совокупности объектов. Основой названия этой совокупности методов послужило английское слово cluster, используемое не одну сотню лет. Его исходное «тривиальное» значение сохранилось в современном языке: в этом случае cluster означает «совокупность близко расположенных объектов или людей». Возможны следующие варианты его перевода на русский: «группа», «скопление», «гроздь», «пучок» и т.д. [17].
Что же означает термин «кластер» в контексте кластерного анализа? Удивительно, но формального и строгого определения этого центрального понятия не существует. По-видимому, так будет и дальше: принято считать, что термин «кластер» субъективен по своей природе и зависит не только от контекста конкретной задачи, но и от запросов и ожиданий пользователя. Что совсем уж субъективно... Особенных затруднений это не вызывает: значение термина интуитивно, а его практическое применение возможно и без строгого определения (как, например, в случае понятия «точка» в геометрии). Чаще всего кластер определяется своей компактностью (большим сходством входящих в него объектов) и изолированностью (непохожестью представителей разных кластеров). Степень сходства/различия определяется как расстояние между изображающими конкретные наблюдения точками в N-мерном пространстве, где оси соответствуют N отдельным признакам (то есть переменным).
- Под естественной группировкой понимается такая, которая основана на объективной близости объектов и полностью определяется их собственными характеристиками. В целом проблема кластеризации сводится к выявлению этой группировки.
- Входными данными для кластеризации служит множество объектов, наблюдений или замеров. Это могут быть не только численные значения, но и категориальные, то есть качественные показатели вроде цвета или наличия/отсутствия определенного морфологического признака.
- Ожидаемый результат — разделение набора данных на подмножества, называемые кластерами. Число таких подмножеств должно быть невелико, а сами объекты — возможно более схожими внутри кластеров и как можно сильнее различными, если принадлежат к разным кластерам [6]. Главное отличие кластеризации от классификации (группирующего обучения с учителем) состоит в том, что перечень групп исходно не задан и определяется самим алгоритмом.
Важно помнить, что неопределенность и необходимость действовать «по наитию» возникает едва ли не на каждом этапе кластеризации. Не помешает рассмотреть эти неопределенности, а заодно и сами шаги:
- Формирование выборки объектов и определение целевых переменных.
- Расчет меры близости.
- Группировка, то есть собственно получение кластеров.
- Представление результатов.
А теперь поподробнее:
- Формирование выборки объектов и определение целевых переменных. Этo этап биоинформатической «пробоподготовки». Прежде всего необходимо определить круг наблюдений/объектов/пациентов/клеток/сообществ/... , которые подвергнутся кластерному анализу. Может потребоваться «чистка» вроде удаления статистических выбросов. Далее получают список переменных, по которым будет оцениваться сходство объектов. Такие более подходящие переменные либо выбирают, либо получают за счет преобразования существующих. Зачастую необходима нормализация данных, то есть приведение их к общему диапазону (чтобы вклад всех переменных был пропорционален). Другая непростая задача на старте — вопрос принципиальной применимости кластеризации. Вообще говоря, его следует решать перед всяким применением кластеризации — чего, разумеется, почти никто не делает. К большому сожалению: ведь алгоритм может успешно кластеризовать любой набор данных, даже откровенный статистический шум безо всяких естественных группировок. Для этого разработано несколько методик — в частности, статистика Хопкинса и метод визуальной оценки «кластерабельности» [17].
- Расчет меры близости. Этот шаг кластерного анализа включает определение сходства имеющихся объектов. Она соответствует расстоянию между точками в многомерном пространстве. Доступны различные способы отложить расстояние в N-мерии:
- евклидово расстояние (наиболее простое — откладывается вдоль прямой и рассчитывается с помощью теоремы Пифагора);
- манхэттенское расстояние (или расстояние городских кварталов, которое откладывает расстояние вдоль координатных осей поочередно);
- обобщающая по отношению к первым двум случаям методика Минковского;
- «шахматное» расстояние Чебышева;
- расстояние Махаланобиса также обобщает расстояния Евклида: оно учитывает корреляции между переменными и нечувствительно к масштабу.
Здесь же, при переходе матрицы расстояний к собственно распределению объектов по кластерам, нужно установить их надлежащее количество k. В дальнейшем это может значительно изменить результаты анализа. Что же мы можем предпринять в этой связи? Получив иерархическую кластеризацию (которая не требует исходно заданного k) и изобразив ее в виде дендрограммы, мы получаем возможность прикинуть, сколько кластеров выделить будет более естественно. Есть и более формальные способы — среди них наиболее распространен «метод локтя» (elbow rule). На соответствующем графике по оси X откладывают рассматриваемое число кластеров, по оси Y — своеобразный «показатель их качества». Перегиб этого графика — локоть — позволяет оценить заветное k.
- Группировка, то есть получение кластеров. Собственно тот этап, для которого существуют все остальные. В результате наши наблюдения оказываются распределенными по группам-кластерам. Различия между методами и алгоритмами кластерного анализа затрагивают прежде всего этот шаг. В случае плоских методик здесь следует просто распределить все имеющиеся наблюдения по кластерам, повторяя эту процедуру для достижения возможно наилучшего результата. Приближает наше разбиение оптимизация определенного параметра, который как раз оценивает, насколько этот результат лучше или хуже прочих.
Там, где плоский алгоритм получит всего одно разбиение, иерархическому предстоит построить множество вложенных. Поэтому-то таксономиям приходится «измерять» расстояние не только между парами объектов, но и между парами объект — промежуточный кластер, а также двумя кластерами. В основе этого критерий объединения, специфичный для конкретных алгоритмов:
- метод одиночной связи (single-link) приравнивает расстояние между кластерами к дистанции между их двумя самыми близкими членами;
- метод полной связи (complete-link) ему противоположен: он считает, что кластерное расстояние задают два самых отдаленных представителя;
- есть и множество методов, оперирующих различными средними значениями — взвешенными (WPGMA), незвешенными (UPGMA) и прочими;
- и снова вспомним метод Уорда с его минимизацией дисперсии в качестве критерия объединения и максимально компактными кластерами.
- Представление кластеров. Данный шаг призван сделать результаты кластерного анализа более понятными и наглядными для человека и его трехмерия — он может быть актуален, а может не требоваться. В нем нет нужды, скажем, если мы имеем дело с сегментацией изображений, когда некоторый снимок (может содержать множество слоев, то есть каналов) следует разбить на однородные области. Задача очень важна в биологии и медицине — в частности, в онкологии, когда важно обозначить точные границы опухоли. Используя их, хирурги смогут удалить всё злокачественное, оставив то, что не затронуто болезнью — это особенно критично в случае опухолей мозга. В этом двумерном случае кластеры самоочевидны — и они «в представлении не нуждаются». В случае же сложных для понимания и визуализации данных полученные кластеры может также потребоваться сделать более понятными биологам в их привычном трехмерии. Здесь приятно отметить, что анализ данных и кластеризация могут иногда предоставляют огромную свободу для творчества и порождать очень художественные изображения.
- На завершающем этапе кластеризации правила хорошего тона предписывают оценивать качество кластеризации на выходе — установить их валидность. Однако и это остается порядочной редкостью...
После того, как мы прошли по стандартному алгоритму шаг за шагом, хотелось бы отметить приятное обстоятельство, отличающее подобные биоинформатические протоколы от «мокробиологических». Почти на каждом этапе у нас есть возможность «откатиться» назад и изменить его в соответствии с полученным опытом. Мы можем неограниченно большое число раз переиграть вычислительный эксперимент или изменить параметры только что проделанного расчета [1], [15].
Но заканчивать разговор о «кластерной кухне» все же приходится довольно удручающими обобщениями. Размытость и неопределенность неразлучны с этой казалось бы точной математической методологией. Она много шире проблем с терминологией (как его собственной, так и упомянутых выше «перекрывающихся» с биологией понятий). Действительно, изобилие доступных методик, плохо предсказуемое качество результатов, затруднения при выборе используемых признаков объектов, различия в форме кластеров, населяющих данные, окаянный вопрос «а они вообще есть в моих данных?..»
Все эти трудности ставят пользователя перед так называемой дилеммой пользователя (user’s dilemma) [1], [15]. Из нее, в частности, следует: мы не можем наперед предугадать, какой метод кластерного анализа или способ отложить расстояние окажется лучше прочих — результат может очень сильно варьировать (рис. 5). Тот же вывод, в общем, следует и из наших упражнений с кластеризацией данных о хищниках. Различные методики дают различающиеся результаты, которые слабо напоминают строгое систематическое родство... В то же время все разбиения могут оказаться целесообразными для решения той или иной задачи.
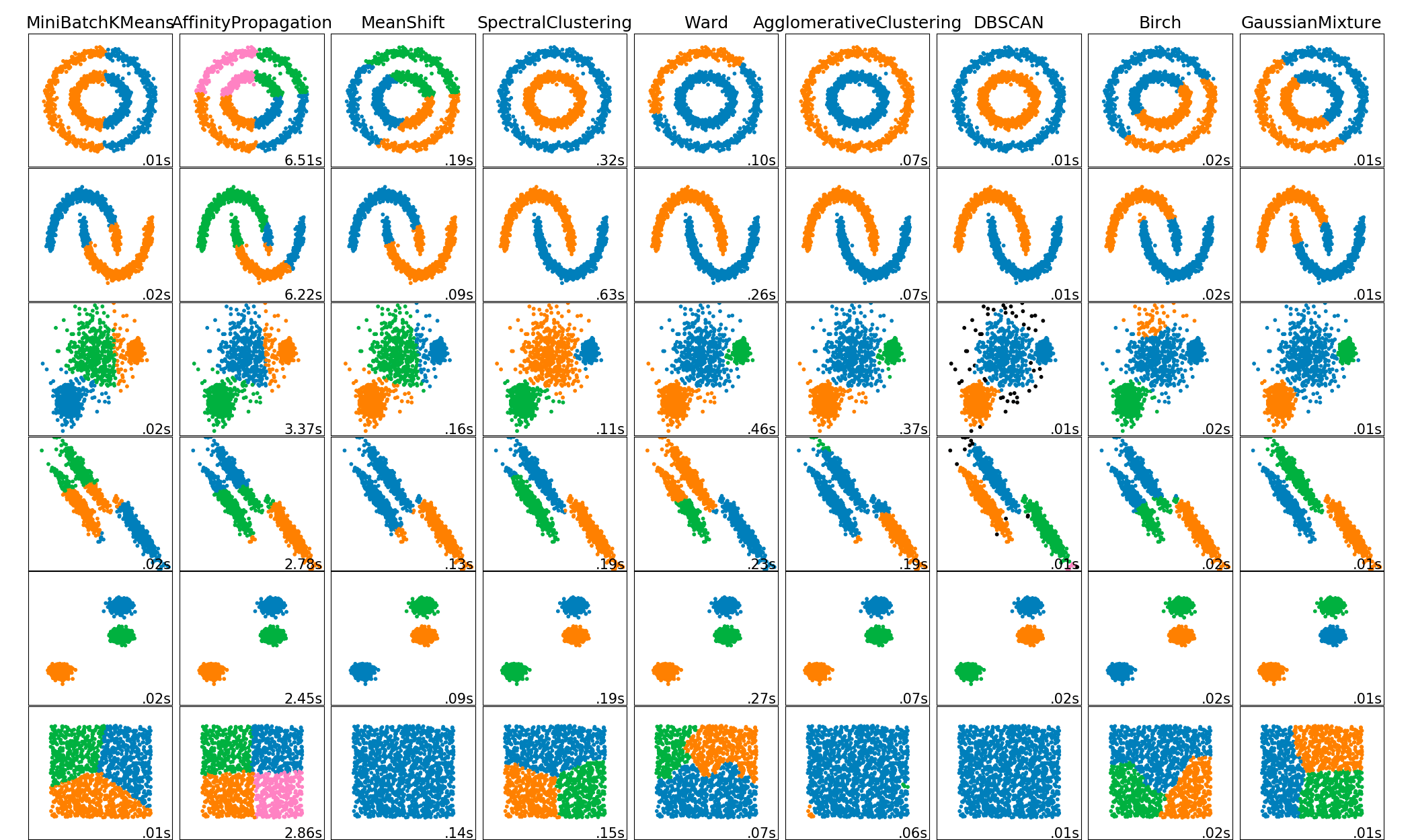
Рисунок 5. Выбор метода кластеризации и сравнения их результатов — не имеющие простого решения задачи. Это подтверждают сильно различающиеся результаты кластеризации. Строки соответствуют наборам данных с различной структурой, столбцы — определенным алгоритмам. Цветами показаны предложенные ими разбиения. Читатель, от природы обладающий превосходной способностью кластеризовать двухмерное пространство, может сравнить их с очевидным для себя разделением точек.
Добивает исчезающую надежду на точную математическую методику, которая «все сама знает и сделает», так называемая теорема невозможности кластеризации Клейнберга (Kleinberg). Ее суть сводится к тому, что идеальных алгоритмов кластеризации не бывает. Клейнберг предложил три желательных свойства, которые неплохо бы иметь алгоритму кластеризации (масштабная инвариантность, согласованность и полнота) и обосновал, что проявляющий все три кластерные «благодетели» на одном датасете алгоритм невозможен [15].
Вместе навсегда
Теперь обратимся к краткой истории кластерного анализа, питая особое пристрастие к его биологическим применениям. Повторимся: бестиарий методов и алгоритмов машинного обучения вообще и кластеризации в частности сам по себе напоминает очередное царство живого. Это in silico «биоразнообразие» стало результатом продолжительного и интенсивного «эволюционного» развития методов ML — и мутировать такие алгоритмы и методы умеют, и приобретать новые прорывные черты в ходе «ароморфозов», и демонстрировать параллельные эволюционные тренды, и даже скрещиваться.
Разные историки науки называют авторами первых методов кластеризации разных исследователей. По-видимому, первой значимой персоналией в этой области стал врач Джон Сноу, один из основоположников анестезиологии и эпидемиологии. Выходит, также и пионер кластерного анализа! Именно вторая медицинская специальность натолкнула доктора Сноу на использование приема, напоминающего кластеризацию. Точнее будет обозначить его как подобие диаграммы Вороного — задачи, ставшей промежуточным шагом одного из самых «ходовых» методов кластеризации (k-средних).
Следующий важный этап кластерного анализа связан с именем польского антрополога Яна Чекановского. В начале 1910-х ученый создал концепцию структурной классификации и сформулировал центральную для кластеризации идею — объединение сходных объектов в однородные компактные группы. Ученый также разработал метод графического представления кластеров, названный диаграммой Чекановского. Как выглядел этот анализ? В матрице приводят числа, описывающие все рассматриваемые наблюдения. Чаще всего отдельному объекту-наблюдению отводят строку, в то время как параметры (переменные) соответствуют столбцам. Каждой группе сходных наблюдений (об их сходстве судят по тому, насколько они скоррелированы) ставится в соответствие некоторый символ или определенная интенсивность штриховки. Далее матрица «пересобирается» таким образом, чтобы схожие наблюдения расположились непосредственно друг за другом (рис. 7а).Очередная веха истории кластерного анализа обычно не упоминается в западных обзорах. В случае литературы на русском языке ей иногда отводят роль первой методики кластерного анализа. Речь идет о трудах советского гидробиолога П.В. Терентьева, который в 1925 году предложил анализировать признаки объектов (не сами объекты!) с помощью метода корреляционных плеяд. Исследователь применял его для анализа сообществ (биоценозов). Метод Терентьева, подобно методу Чекановского, начинается с получения коэффициентов корреляции для исходной матрицы наблюдений (рис. 7б). Далее следует графическое представление — каждый объект изображают в виде кружка, которые соединяют линиями в случае высокой корреляции. Толщина этой линии отображает значение коэффициента (стало быть, и схожесть наблюдений).
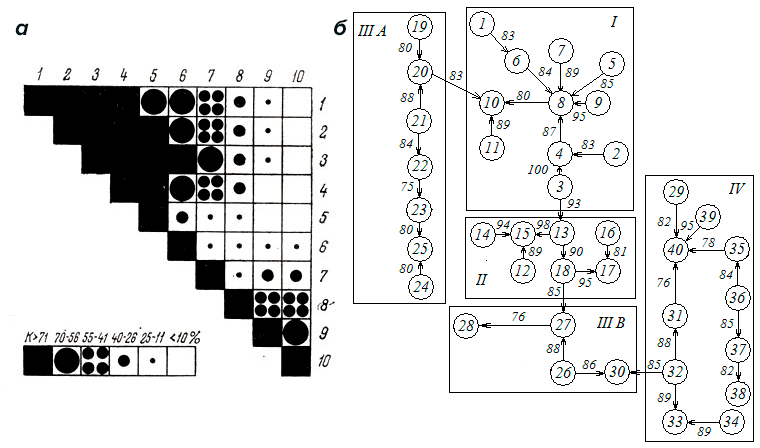
Рисунок 7. «Живые ископаемые» — прародители методов кластерного анализа. а — Диаграмма Чекановского. б — Метод корреляционных плеяд Терентьева.
После такую «корреляционную плеяду» начинают разделять, «разрезая» все линии со значением коэффициента меньше выбранного. Два описанных метода-прародителя (Чекановского и Терентьева), как мы видим, основаны скорее на графических представлениях, чем сложных вычислениях. Позднее их идеи послужили основой для прочих основанных на графах методиках кластеризации. Однако «ушедшими в историю» их назвать нельзя — скорее это «живые ископаемые». Они по-прежнему используются в ряде научных отраслей.
Следующий эпизод истории — это момент, когда кластерный анализ «уж точно возник», то есть был предложен в современном понимании. В этом строгом смысле создателями кластеризации (особенно в западной традиции) называют Драйвера и Кребера (H.E. Driver и A.L. Kroeber). Область интересов этих ученых относится к гуманитарной антропологии (не путать с физическими антропологами — по большей части отечественными — в ведении которых находятся антропогенез, расоведение и прочие черепа). Первое упоминание концепции Драйвера и Кребера приходится на 1932 год и их работу «Количественное выражение культурных взаимосвязей». Книга посвящена этнологии и рассматривает различия между разными культурами, включая первобытные.
В 1938 и 1939 годах кластеризацию применили в психологии, соответственно, Зубин и Трион. Метод им отлично подошел, особенно при исследовании психологических различий между отдельными людьми — в психологии личности. И с этого момента начался продолжающийся в наши дни сериал «Кластеры и психологи». Он имел со своим биологическим аналогом довольно мало пересечений — и во многом такое положение вещей сохранилось. В чем же состоял новый подход? По сути, Зубин продолжил движение в намеченном его предшественниками направлении и разработал очередной способ сортировать матрицы коэффициентов корреляции. Он и его коллеги хотели обойти недостатки широко используемого в среде психологов факторного анализа — либо модифицируя его, либо разработав простую и эффективную альтернативу. В 1939 году в своей монографии Трион категорично обозначил это следующим образом: «Кластерный анализ — это факторный анализ для бедных». Его книга стала первым крупным научным трудом, посвященным непосредственно кластерному анализу и вынесшему само понятие в заглавие.
Вскоре кластеризацию принял на вооружение известный психолог, создатель теории черт Р.Б. Кеттелл. За кластерный анализ Кеттелл взялся очень основательно: он обсуждает четыре разных метода кластеризации, некоторые — подозрительно напоминающие предшествующие работы. Возможное объяснение — банальное незнание о статьях, опубликованных в совершенно другой области знаний. Довольно странно, что даже пристальное внимание такого мэтра психологии как Кеттелл не привлекло к кластерному анализу особого внимания. Действительно, следующее десятилетие (1950-е) связано с падением интереса к кластеризации. В это время примечательно разве что возникновение первого иерархического алгоритма. Зато сразу после последовал расцвет 1960-х годов. Причины такого подъема — создание компьютеров и развитие первых алгоритмов нейронных сетей. Резко возросло число энтузиастов кластеризации — полушутя говорили, что оно может превысить число алгоритмов...
Наибольший энтузиазм в 1960-е гг. методы кластеризации вызвали у специалистов в области ботаники, экологии и общей биологии (в частности, занятых анализом сообществ) и, в меньшей степени, у социологов. Однако решающую роль в «кластерном буме 1960-х» сыграла монография «Начала численной таксономии» Р. Сокэла и П. Снита [18]. Благодаря этой книге кластерный анализ стал известен очень широкому кругу ученых — и они не замедлили вооружиться новым для себя инструментом. В этой и последующих работах авторы (энтомолог и микробиолог) сформулировали новый подход к биологической систематике, названный ими численной таксономией. Нет сомнений, что их наследие повлияло на развитие и биологии как науки в целом. Итак, Сокэл и Снит предложили применять кластерный анализ для учета множества признаков, которые должны описывать организм как можно более полно, характеризуя его морфологию, биохимию, образ жизни и т.д. Это позволяет оценивать степень их эволюционной близости и помещать организмы с высоким сходством в общие систематические группы. Минималистичный пример анализа в русле численной таксономии мы уже проделали — когда строили иерархическую кластеризацию по признакам хищников. Безусловно, до настоящей этот учебный пример не дотягивает из-за немногочисленных и однородных признаков.
Весомым вкладом Сокэла и Снита стало понятие OTU (operational taxonomic unit, «операционная таксономическая единица»). Его применяют для описания некоторой группы организмов, для которых предполагается родство, притом, что говорить о них, как о едином таксоне полных оснований нет. Скажем так: OTU это рассматриваемый в ходе кластерного анализа предполагаемый таксон. Сейчас под OTU понимают прежде всего mOTU — молекулярную операционную таксономическую единицу, которая строится на основании близости участков ДНК. Однако наибольшее влияние работы биологов оказали за счет своего эффекта на мировое «кластерное сообщество» — благодаря численной таксономии кластерный анализ стал по-настоящему широко известен. Сами того не ведая, пример элементарной численной таксономии мы рассмотрели на «хищном» датасете — когда строили иерархическую дендрограмму.К концу 1960-х на смену «кластерному буму» закономерно стал приходить «кластерный упадок». Не слишком осмысленное изобилие методов и алгоритмов и вал сомнительных работ вызывали критические замечания... В этой связи научное сообщество поставило задачу сформулировать критерии оценки и сравнения разных алгоритмов. К 1970-м критика усиливается вплоть до предложений прекратить разработку новых процедур кластеризации и относиться со скептицизмом к ее результатам. Ученых охватил «кластерный пессимизм» и поиски путей целесообразного, разумного применения кластеризации. Последующие же десятилетия стали временем ровного и спокойного развития этой научной отрасли [17], [20].
Работа для кластеров
Напоследок хотелось бы бегло описать, как разнообразная, строгая, математическая и при этом неожиданно субъективная группа методов — кластерный анализ — способна помочь в работе ученого в ХХI веке. Кластеризация поможет установить внутреннюю структуру данных, выделить нетривиальные новые «подводные течения» в них и отметить аномалии — необычные, выпадающие из общего числе наблюдения [18].
- В экологии кластерный анализ пригодится, если требуется выявить пространственную и временную структуру сообществ организмов.
- В геномике — отыщет группировки близких последовательностей нуклеиновых кислот и семейства консервативных генов, выполняющих схожие функции у самых разных организмов.
- Поможет кластерный анализ и при выделении групп людей с определенными генетическими вариациями.
- В соседней с биологией медицине эти методы пригодятся, чтобы выделить типы тканей на трехмерных снимках ПЭТ (позитронно-эмиссионной томографии), выявить шаблоны устойчивости к антибиотикам и группировать эти самые антибиотики по типу антибактериальной активности. В онкологии кластеризация полезна, чтобы выделить, распознать и строго локализовать раковые клетки в контексте здоровой ткани.
- Очередь за науками о человеке (психология, социология и др.) и гуманитариями. Они развили большое разнообразие приложений кластерного анализа — скажем, для описания черт отдельных людей в области психологии личности или социальных групп. Здесь кластеризация испытывает сильную конкуренцию со стороны своего предшественника — дискриминантного анализа.
- Науки о Земле (геология, география, почвоведение и др.) применяют кластерный анализ к отдельным территориям, геологическим формациям, почвам — решая, в том числе, свою любимую задачу районирования.
- Наконец, на точном и инженерном краю науки кластерный анализ служит для фрагментации изображений, распознавания образов, анализа различных сигналов вроде текста и аудиозаписей речи, сжатия данных в информатике, хранения и обработки данных и документов, анализа социальных сетей и многого другого [1].
Однако как быть со всеми проблемами, затруднениями и неопределенностями, неразлучными с кластерным анализом и вместе обозначенными как «дилемма пользователя»? Вряд ли их стоит считать основанием отказываться от этого наглядного и эффективного способа выявить структуру ваших многомерных и больших данных. Особенно биологу — которому к капризной и изменчивой логике не приходится привыкать. Более того, неопределенности и необходимость выбирать — алгоритм кластеризации, способ отложить расстояние между объектами, число кластеров,.. — это простор применить ваши экспертные знания и профессиональное чутье. К тому же неопределенность протокола кластерного анализа не мешает ему оставаться точной вычислительной методикой. И, что очень важно, методикой воспроизводимой. Это означает, что, имея ваш скрипт или иной «сухой» экспериментальный протокол, коллеги и читатели смогут без труда воспроизвести, проверить и изменить его. И эти положительные стороны вместе можно обозначить как мотивирующий «кластерный оптимизм».
Литература
- Anderberg M.R. Cluster analysis for applications. NY: Academic Press, 1973;
- Многомерные пространства. synset.com;
- 12 методов в картинках: секвенирование нуклеиновых кислот;
- «Омики» — эпоха большой биологии;
- Геном человека: как это было и как это будет;
- Сверим часы;
- 12 методов в картинках: «сухая» биология;
- Неканонические аминокислоты. Биомолекулы, о которых не принято говорить;
- Нанопоровое секвенирование: на пороге третьей геномной революции;
- Повтор, еще повтор!;
- Richard C.-A. (2017). Гид по структуре машинного обучения. «Нетология»;
- Википедия: «Стохастическое вложение соседей с t-распределением»;
- Anil K. Jain. (2010). Data clustering: 50 years beyond K-means. Pattern Recognition Letters. 31, 651-666;
- Как прочитать эволюцию по генам?;
- A. K. Jain, M. N. Murty, P. J. Flynn. (1999). Data clustering. ACM Comput. Surv.. 31, 264-323;
- Charpentier A. (2015). k-means clustering and Voronoi sets. R-bloggers;
- Леонов В. Кластерный анализ: основы метода и его применение в биомедицине. «Биометрика»;
- H. Prauser. (2007). Robert R. Sokal und Peter H. A. Sneath, Principles of Numerical Taxonomy 1. Aufl. XVI, 359 S., 38 Abb., 21 Tab. San Francisco and London 1963: W. H. Freeman and Company 60 s. Z Allg Mikrobiol. 6, 139-140;
- Карл Вёзе (1928–2012);
- Roger K. Blashfield, Mark S. Aldenderfer. (1988). The Methods and Problems of Cluster Analysis. Handbook of Multivariate Experimental Psychology. 447-473;
- Blaire van Valkenburgh, Benison Pang, Deborah Bird, Abigail Curtis, Karen Yee, et. al.. (2014). Respiratory and Olfactory Turbinals in Feliform and Caniform Carnivorans: The Influence of Snout Length. Anat. Rec.. 297, 2065-2079.
Источник: biomolecula.ru