Анимация градиентного спуска и ландшафта функции потерь на Python

Статья публикуется в переводе, автор оригинального текста Tobias Roeschl.

В процессе путешествия по изучению различных алгоритмов я набрел на ландшафты функции потерь нейронных сетей с их горноподобными рельефами, хребтами и долинами. Эти ландшафты функции потерь выглядят совсем не похожими на выпуклые и гладкие ландшафты, которые я встречал для линейной и логистической регрессии. В этой статье мы создадим ландшафты функции потерь и анимацию градиентного спуска для набора данных MNIST.

Приведенное выше изображение демонстрирует крайне невыпуклый ландшафт функции потерь нейронной сети. Ландшафт функции потерь – это визуальное представление значений, которые принимает целевая функция на наших тренировочных данных. Поскольку наша цель – визуализация потерь в трех измерениях, мы должны выбрать два параметра, которые будут изменяться, а остальные параметры останутся неизменными. Однако стоит заметить, что существуют продвинутые техники (например, сокращение размерности или filter response normalization), которые можно использовать для аппроксимации ландшафта функции потерь в подпространстве параметров с более низкой размерностью. Трехмерное представление функции потерь нейронной сети VGG с 56 слоями изображено на рис. 1. Однако это выходит за пределы данной статьи.

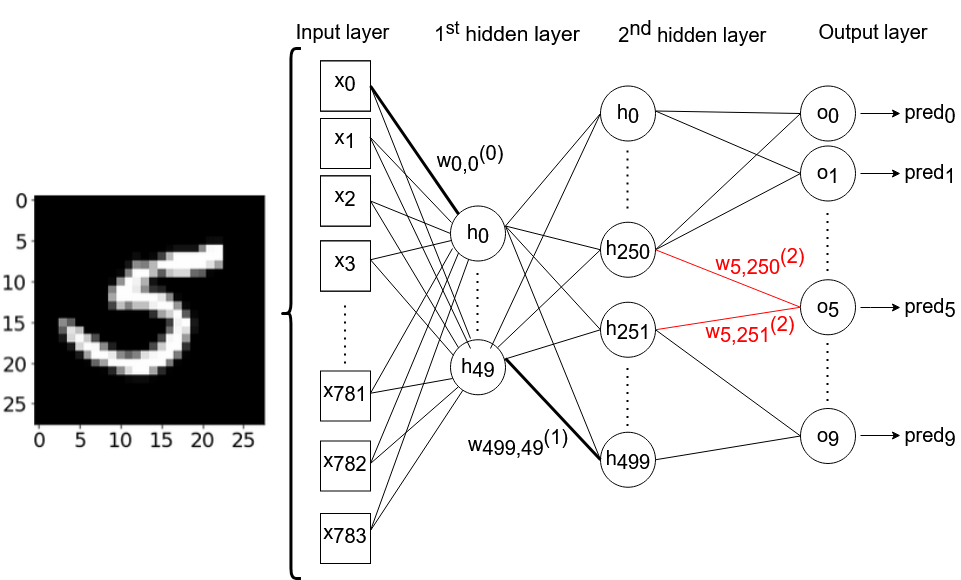
Искусственная нейронная сеть, над которой мы будем работать, состоит из одного входного слоя (с 784 узлами), двух скрытых слоев (с 50 и 500 узлами соответственно) и выходного слоя (с 10 узлами). Мы будем везде использовать сигмоиду в качестве функции активации. Эта нейронная сеть не будет содержать никаких порогов. Тренировочные данные состоят из изображений размером 28*28 пикселей с рукописными цифрами от 0 до 9 из набора данных MNIST. Технически, мы могли бы выбрать любые два веса из 784*50+50*500+500*10 = 69.200 весов, используемых в нашей сети, но я произвольно решил выбрать веса w250,5 (2) и w251,5(2), соединяющие 250-й и 251-й узлы второго скрытого слоя с шестым выходным нейроном, соответственно. Шестой выходной нейрон предсказывает, можно ли на данном изображении увидеть цифру '5'. Следующий рисунок схематически изображает архитектуру нейронной сети, с которой мы собираемся работать. Для простоты и понятности некоторые связи между нейронами – и большинство подписей с весами – были намеренно опущены.

На Python'е мы сначала импортируем набор данных MNIST. Поскольку рукописные цифры в этом наборе представлены в виде изображений с градациями серого цвета, мы можем нормализовать наши входные данные, преобразовав значения пикселей из диапазона 0-255 к диапазону 0-1. разделив эти значения на 255.

         # Импортируем библиотеки import numpy as np import gzip from sklearn.preprocessing import OneHotEncoder import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from scipy.special import expit import celluloid from celluloid import Camera from matplotlib import animation   # Открываем файлы MNIST:  def open_images(filename):     with gzip.open(filename, "rb") as file:              data=file.read()         return np.frombuffer(data,dtype=np.uint8, offset=16).reshape(-1,28,28).astype(np.float32)   def open_labels(filename):     with gzip.open(filename,"rb") as file:         data = file.read()         return np.frombuffer(data,dtype=np.uint8, offset=8).astype(np.float32)       X_train=open_images("C:Users	obia	rain-images-idx3-ubyte.gz").reshape(-1,784).astype(np.float32)  X_train=X_train/255 # rescale pixel values to 0-1  y_train=open_labels("C:Users	obia	rain-labels-idx1-ubyte.gz") oh=OneHotEncoder(categories='auto')  y_train_oh=oh.fit_transform(y_train.reshape(-1,1)).toarray() # one-hot-encoding of y-values     

Чтобы создать ландшафты потерь, мы собираемся нарисовать трехмерный график потерь по отношению к двум упомянутым выше весам w250_5(2) и w251_5(2). Чтобы это сделать, мы должны определить функцию потерь среднеквадратичной ошибки по отношению к весам w_a и w_b. Потери нашей модели равны средней сумме квадратичных ошибок между предсказаниями модели и истинными значениями для каждого из 10 выходных нейронов. Для N примеров эта функция будет выглядеть так:

$$J(y,pred)=\frac{1}{N}\underset{i=1}{\overset{N}{?}}(\underset{k=1}{\overset{10}{?}}(y_{i,k}?pre{d}_{i,k}{)}^2)$$

Здесь y и pred представляют, соответственно, матрицы актуальных и предсказанных значений y. Предсказанные значения рассчитываются прямым проходом входных данных по нейронной сети до выходного слоя. Выход каждого слоя служит входом для следующего слоя. Входная матрица умножается на матрицу весов соответствующего слоя. После этого применяется функция сигмоиды для получения выхода данного конкретного слоя. Эти матрицы весов инициализируются небольшими случайными числами с помощью генератора псевдо-случайных чисел numpy. Используя инициализацию (seed), мы можем обеспечить воспроизводимость данных. После этого мы заменяем два веса, которым разрешено изменяться, аргументами w_a и w_b. На Python мы можем реализовать функцию потерь следующим образом:

         hidden_0=50 # количество узлов первого скрытого слоя  hidden_1=500 # количество узлов второго скрытого слоя   # Зададим функцию потерь: def costs(x,y,w_a,w_b,seed_):           np.random.seed(seed_) # задаем инициализатор генератора случайных чисел          w0=np.random.randn(hidden_0,784)  # матрица весов 1-го скрытого слоя         w1=np.random.randn(hidden_1,hidden_0) # матрица весов 2-го скрытого слоя         w2=np.random.randn(10,hidden_1) # матрица весов выходного слоя         w2[5][250] = w_a # задаем значение веса w_250,5(2)         w2[5][251] = w_b # задаем значение веса w_251,5(2)         a0 = expit(w0 @ x.T)  # выход 1-го скрытого слоя          a1=expit(w1 @ a0)  # выход 2-го скрытого слоя          pred= expit(w2 @ a1) # выход последнего слоя          return np.mean(np.sum((y-pred)**2,axis=0)) # потери w.r.t. w_a и w_b     

Чтобы создать картинку, мы определяем диапазон значений наших весов и строим ячеистую сеть для получения всех возможных комбинаций значений весов w_a и w_b. Для каждой пары w_a и w_b нашей сети мы рассчитываем потери с помощью нашей функции потерь. После этого мы, наконец, можем создать ландшафт функции потерь:

         # Зададим набор значений для ячеистой сети:  m1s = np.linspace(-15, 17, 40)    m2s = np.linspace(-15, 18, 40)   M1, M2 = np.meshgrid(m1s, m2s) # создаем ячеистую сеть    # Определим потери для каждой координаты ячеистой сети:  zs_100 = np.array([costs(X_train[0:100],y_train_oh[0:100].T                                  ,np.array([[mp1]]), np.array([[mp2]]),135)                           for mp1, mp2 in zip(np.ravel(M1), np.ravel(M2))]) Z_100 = zs_100.reshape(M1.shape) # Значения z для N=100  zs_10000 = np.array([costs(X_train[0:10000],y_train_oh[0:10000].T                                  ,np.array([[mp1]]), np.array([[mp2]]),135)                          for mp1, mp2 in zip(np.ravel(M1), np.ravel(M2))]) Z_10000 = zs_10000.reshape(M1.shape) # Значения z для N=10,000   # Рисуем ландшафты функции потерь:  fig = plt.figure(figsize=(10,7.5)) # создаем фигуру ax0 = fig.add_subplot(121, projection='3d' ) ax1 = fig.add_subplot(122, projection='3d' )  fontsize_=20 # задаем размер шрифта для меток осей  labelsize_=12 # задаем размер меток делений   # Настраиваем дочерние рисунки (subplots):  ax0.view_init(elev=30, azim=-20) ax0.set_xlabel(r'$w_a$', fontsize=fontsize_, labelpad=9) ax0.set_ylabel(r'$w_b$', fontsize=fontsize_, labelpad=-5) ax0.set_zlabel("costs", fontsize=fontsize_, labelpad=-30) ax0.tick_params(axis='x', pad=5, which='major', labelsize=labelsize_) ax0.tick_params(axis='y', pad=-5, which='major', labelsize=labelsize_) ax0.tick_params(axis='z', pad=5, which='major', labelsize=labelsize_) ax0.set_title('N:100',y=0.85,fontsize=15) # задаем заголовок дочернего рисунка  ax1.view_init(elev=30, azim=-30) ax1.set_xlabel(r'$w_a$', fontsize=fontsize_, labelpad=9) ax1.set_ylabel(r'$w_b$', fontsize=fontsize_, labelpad=-5) ax1.set_zlabel("costs", fontsize=fontsize_, labelpad=-30) ax1.tick_params(axis='y', pad=-5, which='major', labelsize=labelsize_) ax1.tick_params(axis='x', pad=5, which='major', labelsize=labelsize_) ax1.tick_params(axis='z', pad=5, which='major', labelsize=labelsize_) ax1.set_title('N:10,000',y=0.85,fontsize=15)  # Поверхностные графики потерь (= ландшафты функции потерь):   ax0.plot_surface(M1, M2, Z_100, cmap='terrain', #поверхностный график                              antialiased=True,cstride=1,rstride=1, alpha=0.75) ax1.plot_surface(M1, M2, Z_10000, cmap='terrain', #поверхностный график                              antialiased=True,cstride=1,rstride=1, alpha=0.75) plt.tight_layout() plt.show()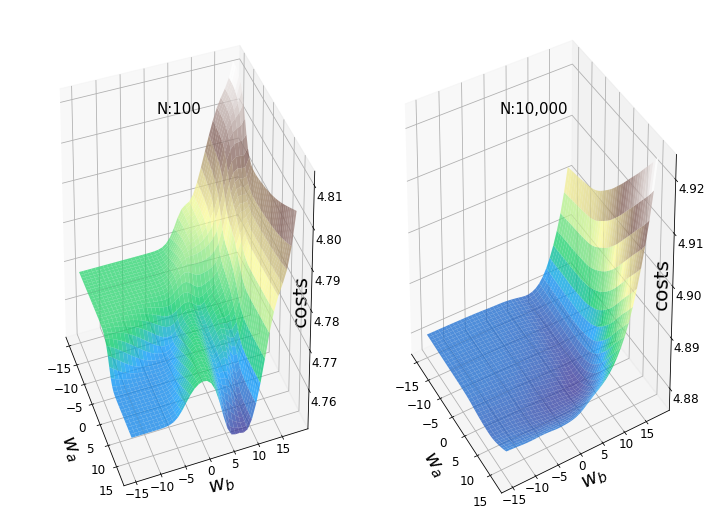     

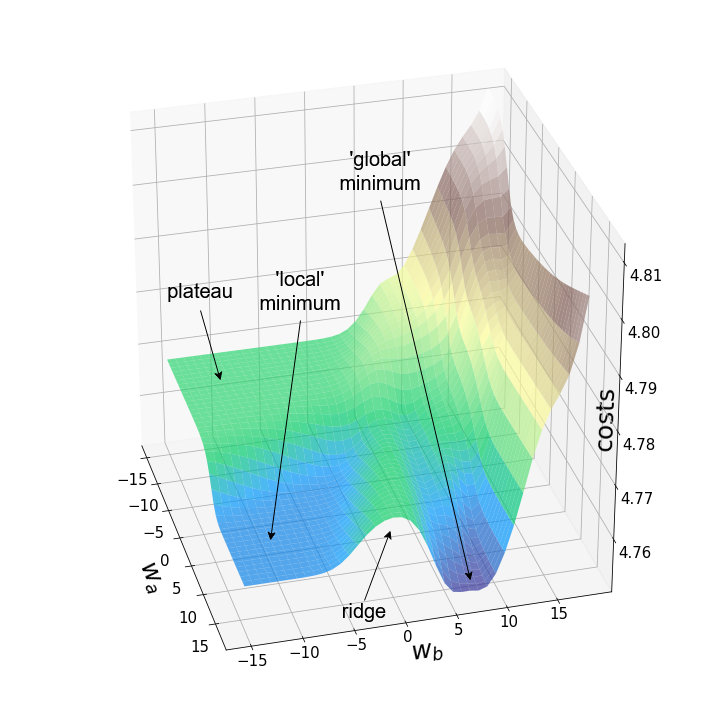
Рисунок 3 изображает два примера ландшафтов функции потерь для одних и тех же весов (w250_5(2) и w251_5(2)) и одинаковых начальных значений всех весов. Левый ландшафт был построен на первых 100 изображениях из набора данных MNIST, а правый – на первых 10.000 изображениях. При ближайшем рассмотрении левого графика там можно увидеть типичные особенности невыпуклых поверхностей: локальные минимумы, плато, хребты (иногда называемые "седловыми точками") и "глобальный" минимум. Однако термин "минимум" следует использовать осторожно, поскольку мы видели лишь небольшой набор значений, и не проводили анализ производной.

Градиентный спуск

Эти "географические барьеры" – полная противоположность выпуклым и гладким ландшафтам функции потерь, которые можно увидеть для линейной регрессии или логистической регрессии. Считается, что эти "барьеры" замедляют или даже препятствуют достижению глобального минимума методом градиентного спуска, и, следовательно, оказывают негативное влияние на качество модели. Чтобы исследовать это явление, я решил анимировать градиентный спуск для данного ландшафта функции потерь из трех различных "стартовых позиций". Градиентный спуск, в целом, заключается в обновлении параметров модели (в данном случае – весов) в соответствии со следующим уравнением:

$$w_{e+1}=w_e??\mathrm{?}J(w_e)$$

Здесь Delta J представляет градиент функции потерь, w – веса всей модели, e представляет текущую эпоху обучения, а aplha – скорость обучения.

Поскольку оба веса в нашем примере соединяются с выходным слоем нейронной сети, достаточно получить частные производные по этим весам для последнего слоя. Чтобы сделать это, мы применяем цепное правило и получаем следующее:

$$\frac{?J}{?w_{ij}^{(2)}}=\frac{?J}{?ou{t}_i^{(2)}}\frac{?ou{t}_i^{(2)}}{?i{n}_i^{(2)}}\frac{?i{n}_i^{(2)}}{?w_{ij}^{(2)}}$$

Здесь w_ij определяется как вес между j-м узлом предыдущего слоя и i-м узлом текущего слоя, которым в нашем случае является выходной слой. Вход i-го нейрона выходного слоя обозначен просто как in_i⁽²⁾, что эквивалентно сумме активаций предыдущего слоя, умноженных на соответствующие веса связей, ведущих к этому узлу. Выход i-го нейрона выходного слоя обозначен как out_i⁽²⁾, что соответствует сигмоиде(in_i⁽²⁾). Решая приведенное выше уравнение, мы получаем:

$$\frac{?J}{?w_{ij}^{(2)}}=(ou{t}_i^{(2)}?targe{t}_i)?ou{t}_i^{(2)}?(1?ou{t}_i^{(2)})?ou{t}_j^{(1)}$$

Здесь out_j⁽¹⁾ соответствует активации j-го узла предыдущего слоя, соединенного с i-м нейроном выходного слоя связью с весом w_ij. Переменная target_i соответствует целевому выводу каждого из 10 нейронов выходного слоя. Возвращаясь к Рис. 2, out_j⁽¹⁾ будет соответствовать активации h₂₅₀ или h₂₅₁, в зависимости от веса, по которому мы хотим рассчитать частную производную. Прекрасное объяснение обратного распространения (backpropagation), включая математические детали дифференцирования, можно найти здесь.

Поскольку выход нейронов выходного слоя эквивалентен предсказаниям всей нашей нейронной сети, мы используем удобное сокращение pred в следующем коде. Поскольку концентрация на одном конкретном узле может привести к коду, сводящему с толку, мы будем придерживаться уже взятого принципа использовать матрицы весов и перемножение матриц для одновременного обновления всех весов выходного слоя. Наконец, мы будем обновлять только те два веса выходного слоя, которые собирались обновлять с самого начала. На Python'е мы реализуем наш алгоритм градиентного спуска только для двух весов следующим образом:

         # Сохраняем значения потерь и весов в списках:  weights_2_5_250=[]  weights_2_5_251=[]  costs=[]   seed_= 135 # для инициализации генератора случайных чисел N=100 # размер выборки   # Задаем нейронную сеть:  class NeuralNetwork(object):     def __init__(self, lr=0.01):         self.lr=lr         np.random.seed(seed_) # Инициализируем генератор случайных чисел         # Инициализируем матрицы весов:          self.w0=np.random.randn(hidden_0,784)           self.w1=np.random.randn(hidden_1,hidden_0)         self.w2=np.random.randn(10,hidden_1)         self.w2[5][250] = start_a # задать стартовое значение для w_a         self.w2[5][251] = start_b # задать стартовое значение для w_b          def train(self, X,y):         a0 = expit(self.w0 @ X.T)           a1=expit(self.w1 @ a0)           pred= expit(self.w2 @ a1)         # Частные производные функции потерь w.r.t. весов выходного слоя:          dw2= (pred - y.T)*pred*(1-pred)  @ a1.T / len(X)   # ... среднее по выборке         # Обновляем веса:          self.w2[5][250]=self.w2[5][250] - self.lr * dw2[5][250]          self.w2[5][251]=self.w2[5][251] - self.lr * dw2[5][251]          costs.append(self.cost(pred,y)) # дописываем значения потерь в список          def cost(self, pred, y):         return np.mean(np.sum((y.T-pred)**2,axis=0))      # Начальные значения w_a/w_b:  starting_points = [  (-9,15),(-10.1,15),(-11,15)]   for j in starting_points:     start_a,start_b=j     model=NeuralNetwork(10) # установить скорость обучения в 10     for i in range(10000):  # 10,000 эпох                    model.train(X_train[0:N], y_train_oh[0:N])          weights_2_5_250.append(model.w2[5][250]) # дописываем значения весов в список         weights_2_5_251.append(model.w2[5][251]) # дописываем значения весов в список  # Create sublists of costs and weight values for each starting point:  costs = np.split(np.array(costs),3)  weights_2_5_250 = np.split(np.array(weights_2_5_250),3) weights_2_5_251 = np.split(np.array(weights_2_5_251),3)     

Поскольку мы обновляем только два веса из многих тысяч весов модели, потери будут падать лишь незначительно, несмотря на сравнительно высокую скорость обучения alpha=10. Это также является причиной того, что веса, которые мы собирались изменять, существенно меняются, тогда как остальные веса меняются лишь незначительно при обновлении весов всей модели. Теперь мы можем анимировать три траектории градиентного спуска для трех различных начальных точек.

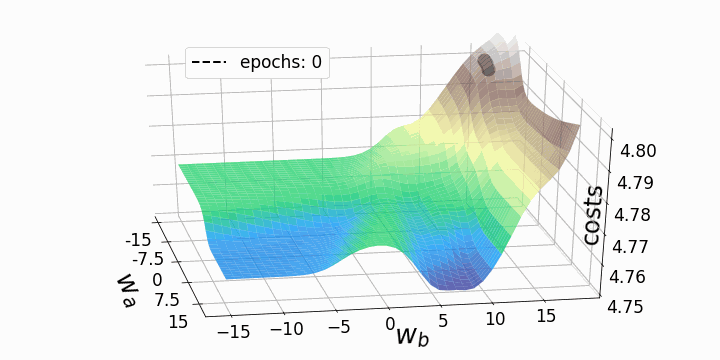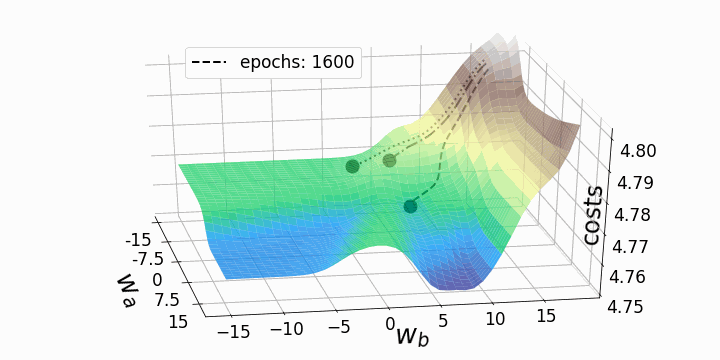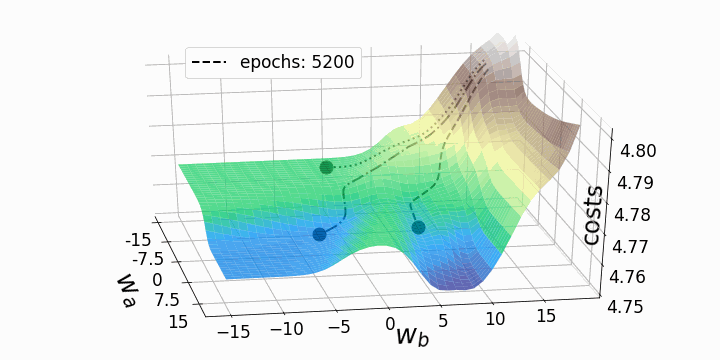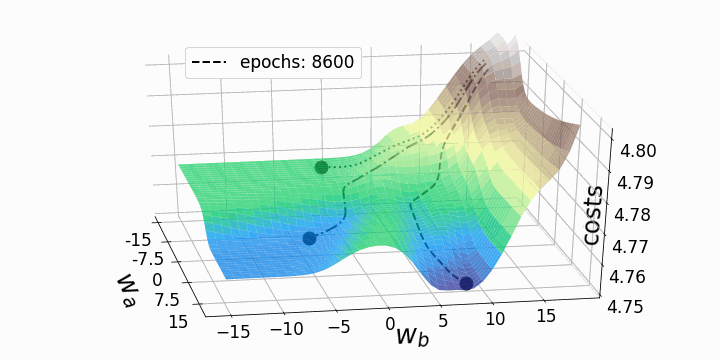
         fig = plt.figure(figsize=(10,10)) # создаем фигуру ax = fig.add_subplot(111,projection='3d' )  line_style=["dashed", "dashdot", "dotted"] # стили линий fontsize_=27 # задаем размер шрифта для меток осей  labelsize_=17 # задаем размер шрифта для меток делений ax.view_init(elev=30, azim=-10) ax.set_xlabel(r'$w_a$', fontsize=fontsize_, labelpad=17) ax.set_ylabel(r'$w_b$', fontsize=fontsize_, labelpad=5) ax.set_zlabel("costs", fontsize=fontsize_, labelpad=-35) ax.tick_params(axis='x', pad=12, which='major', labelsize=labelsize_) ax.tick_params(axis='y', pad=0, which='major', labelsize=labelsize_) ax.tick_params(axis='z', pad=8, which='major', labelsize=labelsize_) ax.set_zlim(4.75,4.802) # задаем диапазон значений по z в графике  # Определяем, график каких эпох рисовать: p1=list(np.arange(0,200,20)) p2=list(np.arange(200,9000,100)) points_=p1+p2  camera=Camera(fig) # создаем объект Camera for i in points_:     # Рисуем три траектории градиентного спуска...     #... каждая начинается из своей начальной точки     #... и имеет собственный уникальный стиль линии:     for j in range(3):          ax.plot(weights_2_5_250[j][0:i],weights_2_5_251[j][0:i],costs[j][0:i],                 linestyle=line_style[j],linewidth=2,                 color="black", label=str(i))         ax.scatter(weights_2_5_250[j][i],weights_2_5_251[j][i],costs[j][i],                    marker='o', s=15**2,                color="black", alpha=1.0)     # Surface plot (= loss landscape):     ax.plot_surface(M1, M2, Z_100, cmap='terrain',                               antialiased=True,cstride=1,rstride=1, alpha=0.75)     ax.legend([f'epochs: {i}'], loc=(0.25, 0.8),fontsize=17) # позиция надписи     plt.tight_layout()      camera.snap() # сделать снимок после каждой итерации      animation = camera.animate(interval = 5, # интервал между фреймами в миллисекундах                           repeat = False,                           repeat_delay = 0) animation.save('gd_1.gif', writer = 'imagemagick', dpi=100)  # сохраним анимацию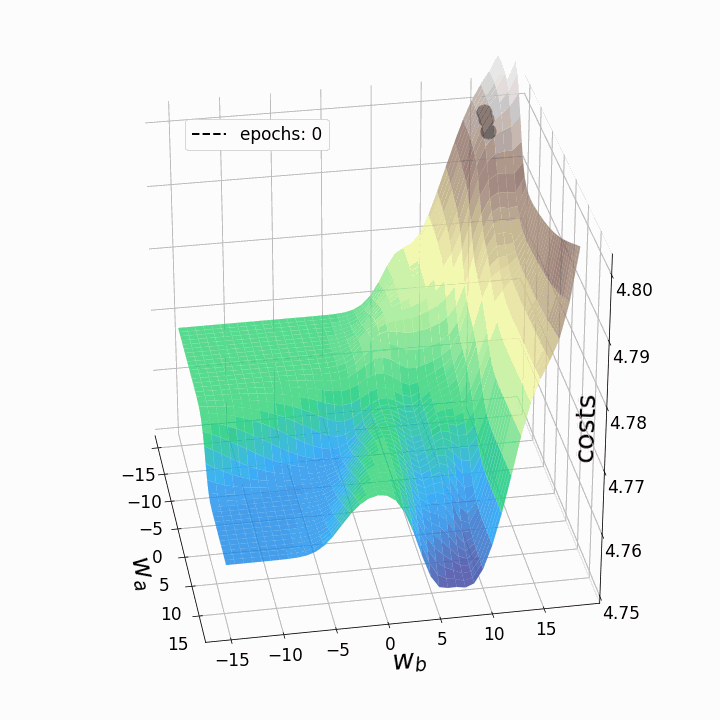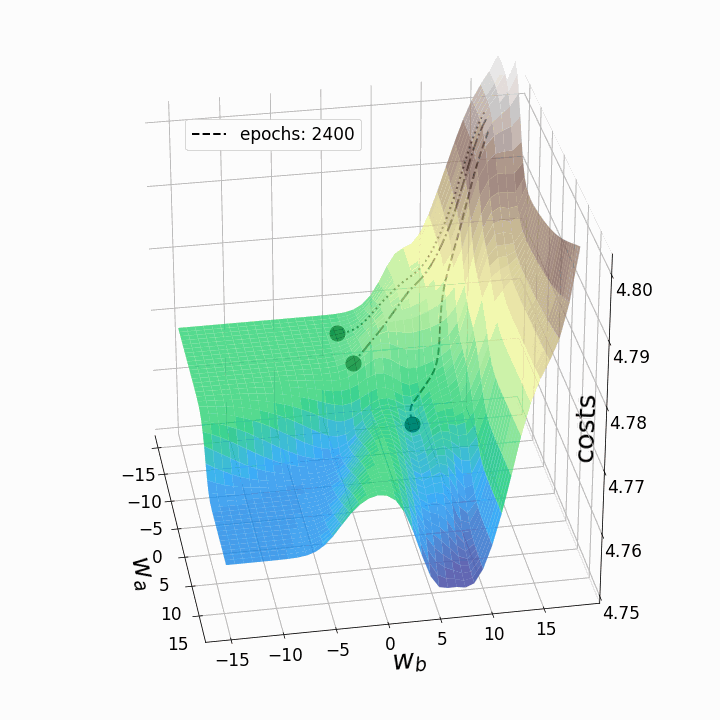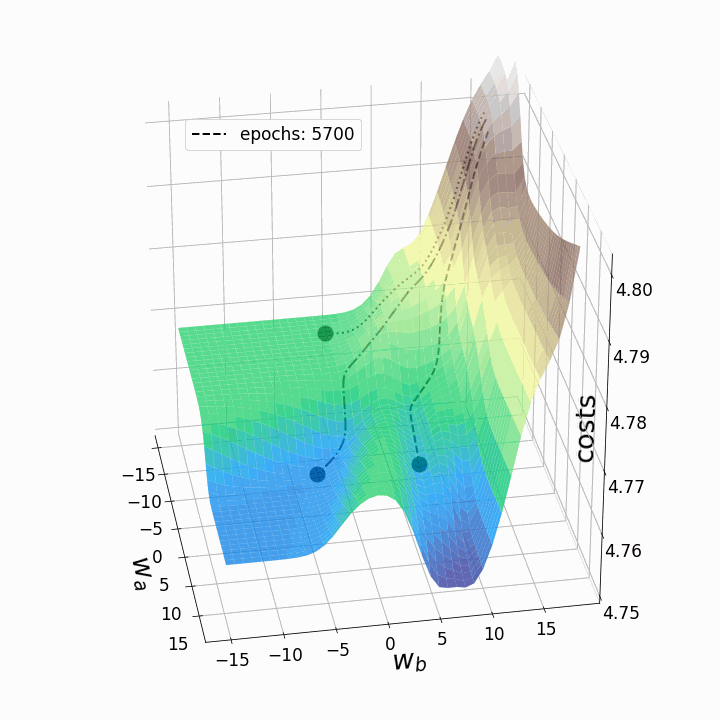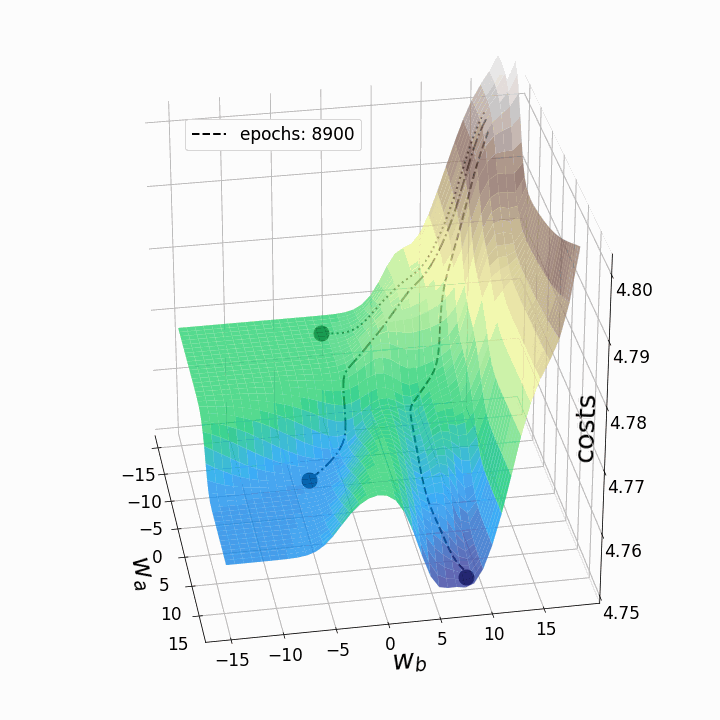       

Как и ожидалось, невыпуклость ландшафта функции потерь делает возможными различные пути градиентного спуска в зависимости от начальных значений наших двух весов. Это приводит к различным значениям функции потерь после заданного количества эпох, и, следовательно, разному качеству моделей. Контурный график предлагает другой взгляд на ту же функцию потерь.

         fig = plt.figure(figsize=(10,10)) # создаем фигуру ax0=fig.add_subplot(2, 1, 1)  ax1=fig.add_subplot(2, 1, 2)   # Задаем параметры дочерних рисунков (subplots):  ax0.set_xlabel(r'$w_a$', fontsize=25, labelpad=0) ax0.set_ylabel(r'$w_b$', fontsize=25, labelpad=-20) ax0.tick_params(axis='both', which='major', labelsize=17) ax1.set_xlabel("epochs", fontsize=22, labelpad=5) ax1.set_ylabel("costs", fontsize=25, labelpad=7) ax1.tick_params(axis='both', which='major', labelsize=17)  contours_=21 # задаем количество контурных линий points_=np.arange(0,9000,100) # определяем, какие эпохи рисовать  camera = Camera(fig) # создаем объект Camera for i in points_:     cf=ax0.contour(M1, M2, Z_100,contours_, colors='black', # контурный график                      linestyles='dashed', linewidths=1)     ax0.contourf(M1, M2, Z_100, alpha=0.85,cmap='terrain') # контурные графики с заливкой           for j in range(3):         ax0.scatter(weights_2_5_250[j][i],weights_2_5_251[j][i],marker='o', s=13**2,                color="black", alpha=1.0)         ax0.plot(weights_2_5_250[j][0:i],weights_2_5_251[j][0:i],                 linestyle=line_style[j],linewidth=2,                 color="black", label=str(i))                  ax1.plot(costs[j][0:i], color="black", linestyle=line_style[j])     plt.tight_layout()     camera.snap()      animation = camera.animate(interval = 5,                           repeat = True, repeat_delay = 0)  # создаем анимацию  animation.save('gd_2.gif', writer = 'imagemagick')  # сохраняем анимацию в gif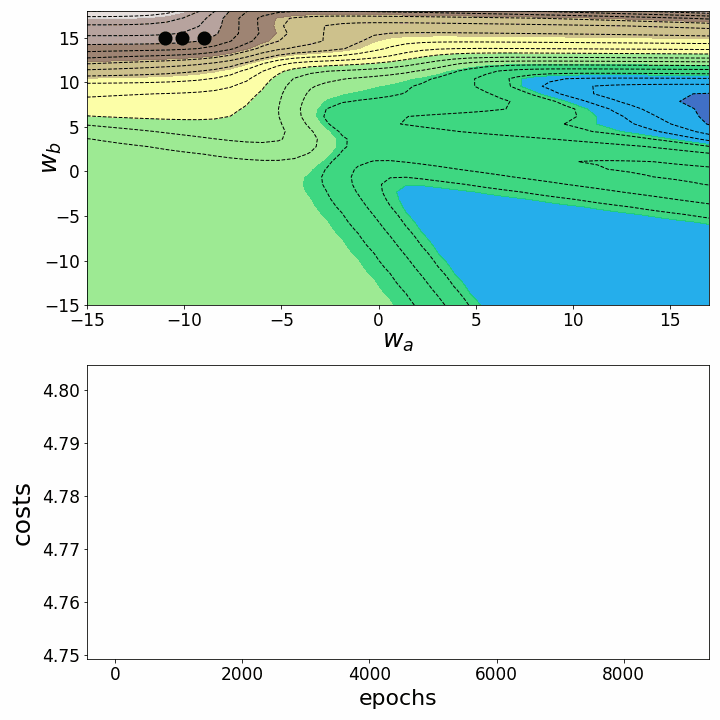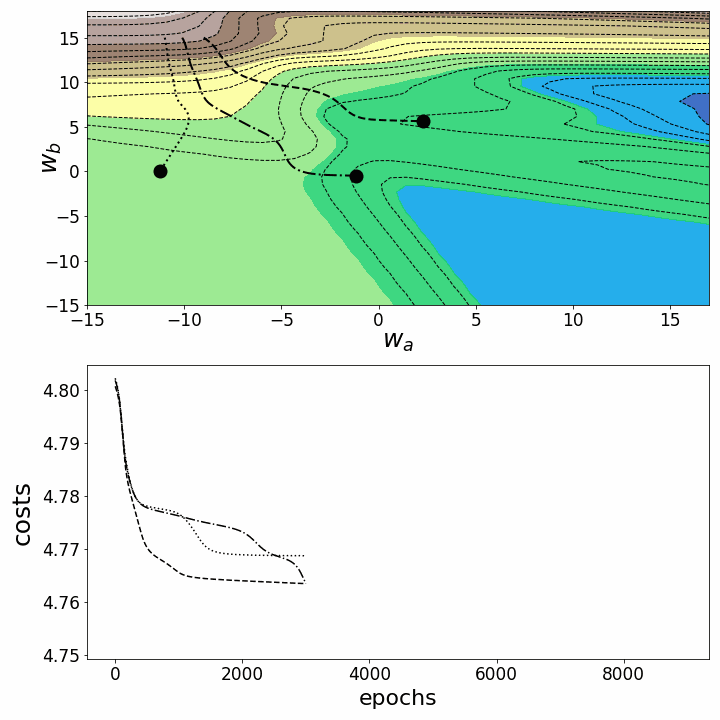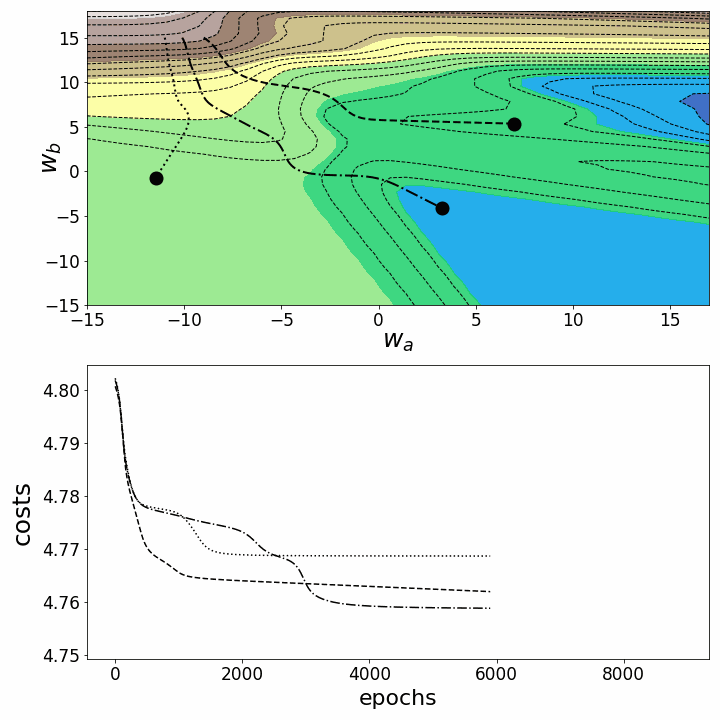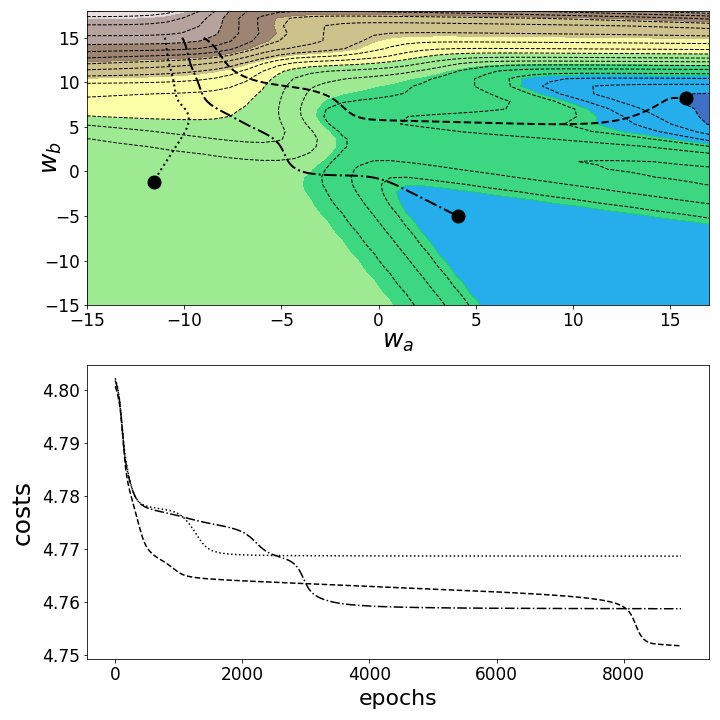     

Обе анимации иллюстрируют, что при невыпуклом ландшафте функции потерь градиентный спуск может "зависнуть" на локальном минимуме, седловой точке или плато. Для преодоления некоторых из этих проблем было изобретено множество вариантов градиентного спуска (ADAGRAD, Adam и т.д.) Однако я хочу разъяснить, что не все ландшафты функции потерь сильно невыпуклые в заданном диапазоне значений w_a и w_b. Выпуклость функции потерь зависит, среди прочего, от количества скрытых слоев – у глубоких нейронных сетей ландшафт функции потерь обычно сильно невыпуклый.

Я решил создать несколько произвольных ландшафтов функции потерь путем изменения числа, инициализирующего генератор случайных чисел. На этот раз веса, которым разрешено меняться, находятся на втором скрытом слое (код). Репрезентативная выборка ландшафтов функции потерь, которые я встретил, применяя этот подход, показана ниже. Размеры выборки и индексы весов, обозначенных как w_a и w_b, указаны в подписях рисунков.

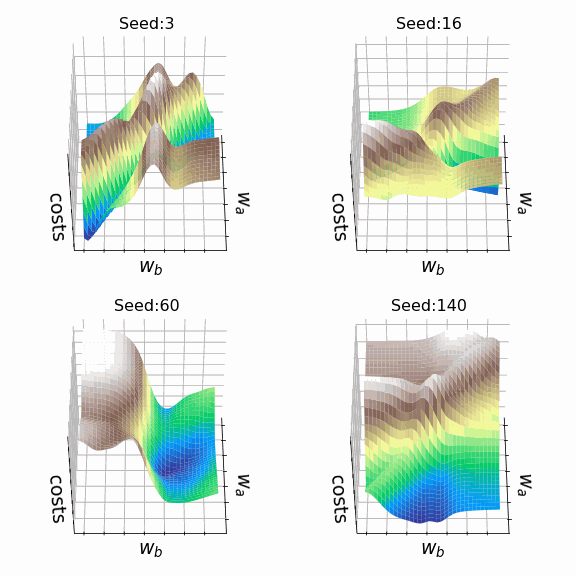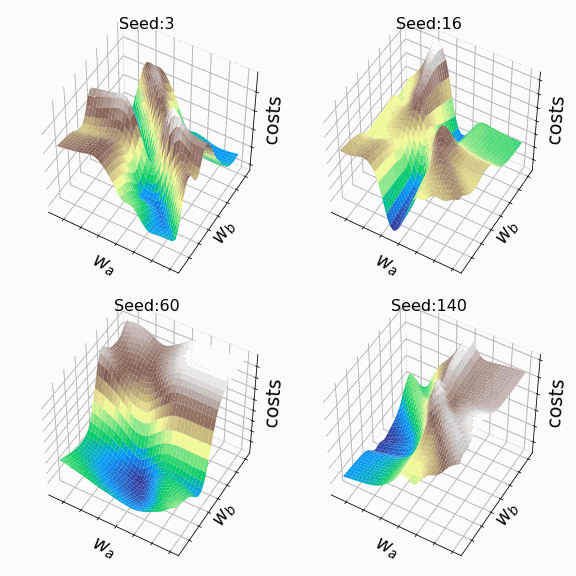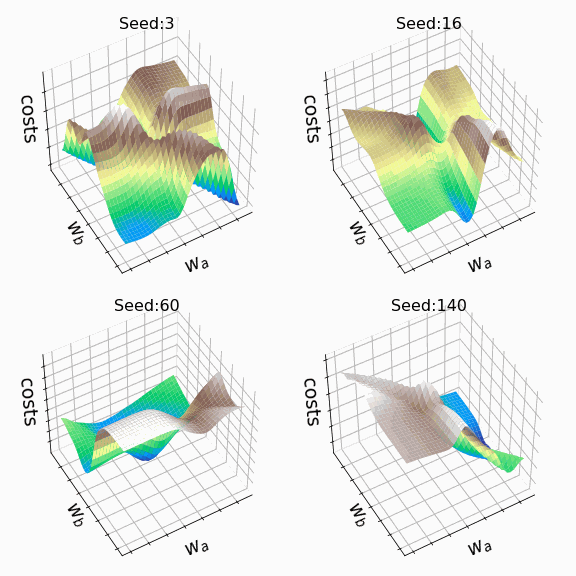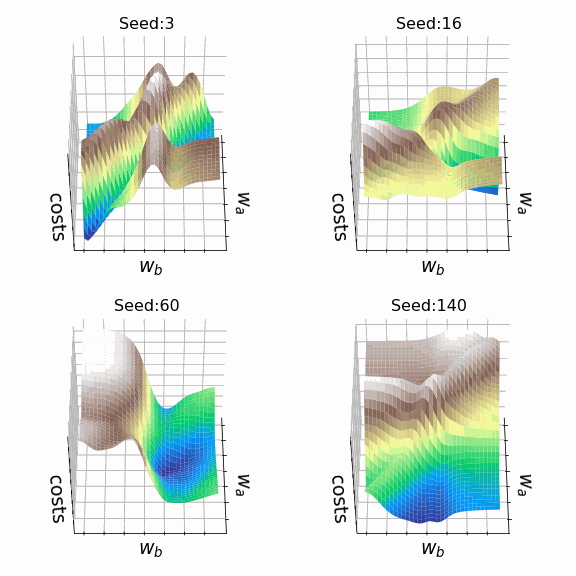
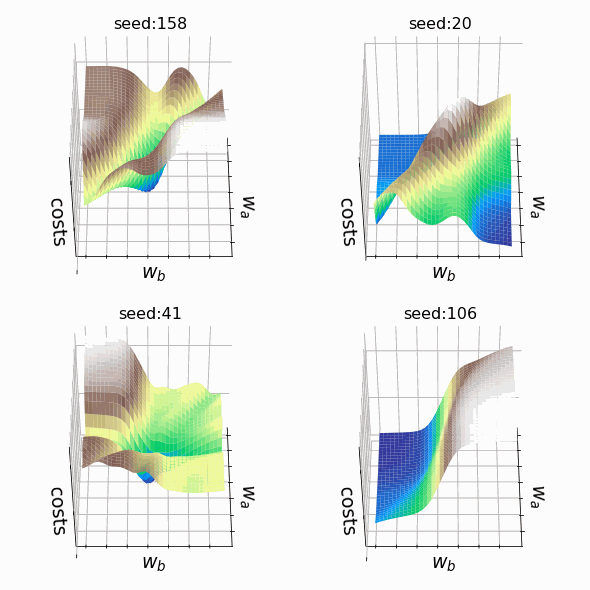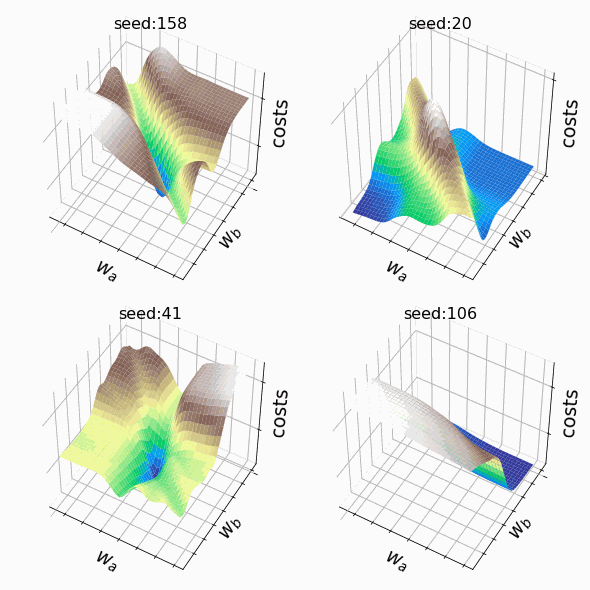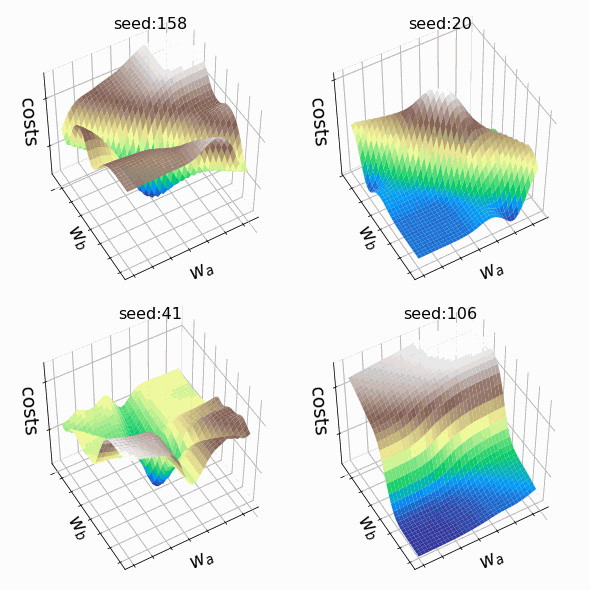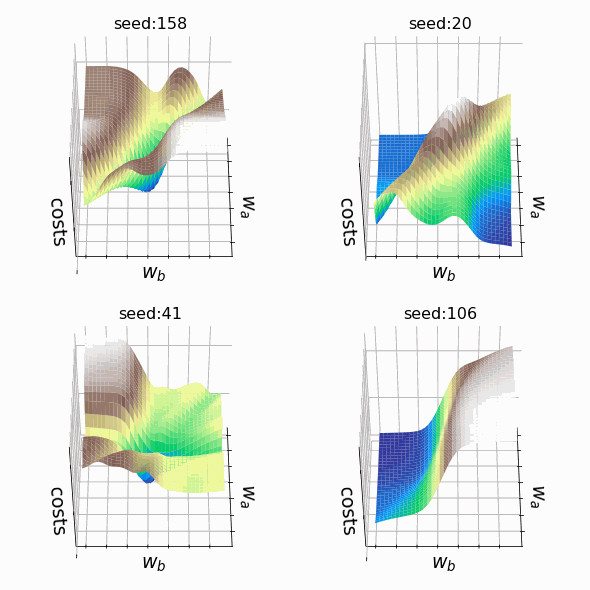
Визуализация ландшафта функции потерь может быть полезна для лучшего понимания теории, лежащей в основе нейронных сетей, и потенциальных недостатков различных алгоритмов оптимизации. На практике, однако, фактическая значимость локальных минимумов, плато и хребтов по-прежнему является предметом споров. Некоторые авторы утверждают, что локальные минимумы в пространствах с большим количеством измерений встречаются очень редко, и что седловые точки могут представлять даже большую проблему для оптимизации параметров, чем локальные минимумы. Другие источники даже предполагают, что минимизация функции потерь до локального минимума является достаточной и может предотвратить переобучение.

Полный блокнот с исходными текстами визуализации можно найти в моем GitHub'е.

Ссылки

База рукописных цифр MNIST (Янн ЛеКун, Коринна Кортес и Крис Буржс).

1. Ли Хао и др. "Визуализация ландшафтов функции потерь нейронных сетей". Достижения нейронных систем обработки информации, 2018.
2. https://machinelearningmastery.com/how-to-normalize-center-and-standardize-images-with-the-imagedatagenerator-in-keras/
3. https://machinelearningmastery.com/why-training-a-neural-network-is-hard/
4. https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/
5. Мэттью Стэйб, Сашанк Дж. Редди, Сэтьен Кэйл, Санджив Кумар, Суврит Сра. "Избежание седловых точек адаптивными градиентными методами" (2019).
6. Ян Дофин и др. "Обнаружение и уничтожение проблемы седловых точек при невыпуклой оптимизации в пространстве с большим количеством измерений". NIPS (2014).
7. А. Хороманска, М. Хенафф, М. Матье, Г.Б. Аруз и Я. ЛеКун. "Ландшафты функции потерь нейронных сетей со множеством слоев". Журнал исследований машинного обучения, 38, 192-204.

Приложение