Всемогущий кубит
МЕНЮ
Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту
ТЕМЫ
Новости ИИ
Голосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Нейронные сети начинающим
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Авторизация
2020-12-21 13:40

Стоит ли ожидать повсеместного появления квантовых компьютеров
Говоря о квантовом компьютере, обычный человек, как правило, представляет супермашину, способную за доли секунды обрабатывать огромные объемы информации. Так ли это, что на самом деле представляет собой квантовый компьютер и появится ли он в ближайшее десятилетие на наших столах, ПостНауке рассказал физик и специалист в области квантовых вычислений Станислав Страупе.
Это материал из гида «Квантовый компьютер». Партнер гида — Академия Росатома.
Не 1, не 0: как работает квантовый компьютер
Отличие квантового компьютера от классического заключается в том, что в первом случае информация хранится в состояниях квантово-механических систем, причем они могут быть разной природы.
В классических вычислениях мы обычно оперируем двоичным кодом, то есть записываем информацию в виде последовательности нулей и единиц (битов), и так мы можем представить в принципе любую информацию. Элементарной же единицей информации в квантовых компьютерах являются так называемые кубиты (qubits = quantum bits). Это какие-то квантовые системы с двумя хорошо определенными базисными состояниями — назовем их |0? и |1?. В отличие от классики, эти два состояния не ограничивают все возможные состояния квантовой системы, потому что существует принцип суперпозиции. Он утверждает, что если квантово-механическая система может находиться в каких-то состояниях, то она может находиться и в любой суперпозиции этих состояний. Геометрически для кубита пространство возможных состояний можно представить как сферу — сферу Блоха. Северный и южный полюс у нее — это |0? и |1?, а все остальные точки на поверхности сферы — другие возможные состояния. Например, на экваторе сферы будет находиться (|0? + |1?)/?2. Значит, состояние кубита — это вектор в пространстве размерности два, поэтому, в отличие от обычного двоичного кода, у нас появляются дополнительные возможности: состояния, которые в классических бинарных системах не могут быть реализованы в принципе, например (|0? + |1?)/?2, и все множество других суперпозиционных состояний. Это и используется в квантовых алгоритмах.
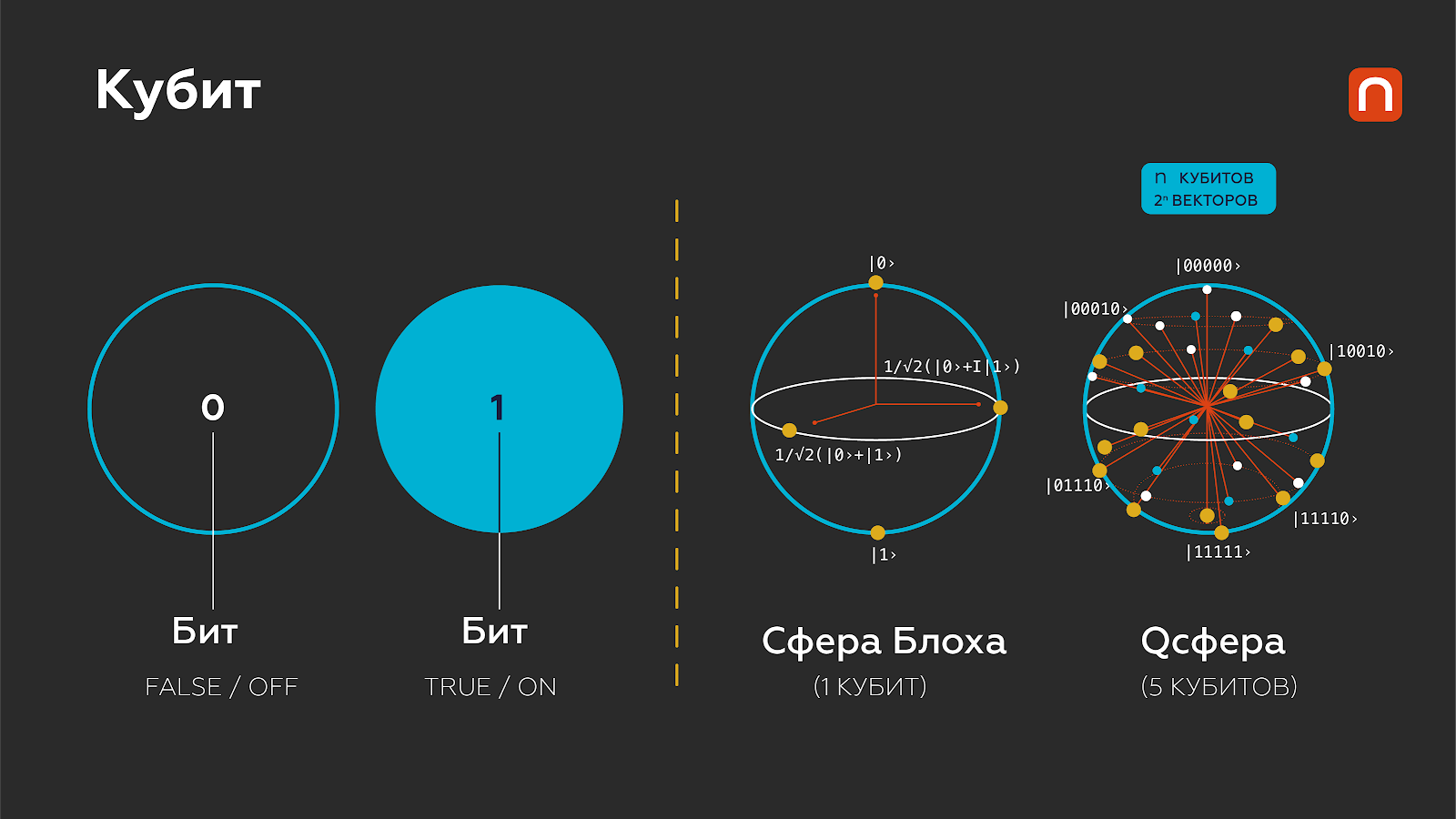
Юлия Кузьмина для ПостНауки
Важным свойством квантовых компьютеров является то, что суперпозиционные состояния не всегда непосредственно доступны нам для измерения. Грубо говоря, мы настраиваем экспериментальный прибор так, чтобы он щупал квантовую систему только определенным образом — например, проверял, находится эта система в состоянии |0? или в состоянии |1?. Как только мы начинаем проводить измерения, у нас происходит коллапс до двоичного кода: результаты будут бинарными, |0? или |1?. Квантовый алгоритм — это все посередине между моментом инициализации начального состояния системы и измерением ее конечного состояния. В терминах пресловутого кота Шрёдингера это то, что происходит в коробке до тех пор, пока мы ее не открыли. Коллапс при измерении — это не проблема, потому что квантовые алгоритмы используют эти суперпозиции в процессе вычисления до проведения измерения. Но на одном кубите далеко не уедешь, кубитов должно быть много.
Критерии выбора физических систем для построения квантового компьютера
Для построения квантового компьютера существуют критерии Ди Винченцо. Известный физик Давид Ди Винченцо сформулировал набор из пяти критериев, которым должна удовлетворять физическая система, чтобы быть хорошим квантовым компьютером. Из них становится понятно, как работает типичный квантовый алгоритм.
- Нужно иметь масштабируемую систему из кубитов — грубо говоря, иметь возможность взять их много. При этом надо понимать, где у вас бит номер 1, а где бит номер 5, то есть иметь возможность индивидуальной адресации кубитов.
- Необходимо уметь инициализировать начальное состояние системы. Это то, с чего начинаются вычисления.
- Следует иметь возможность провести собственно вычисления. Для этого нужно уметь делать универсальный набор операций, который позволит сконструировать произвольное преобразование системы кубитов. Эти операции называют логическими гейтами. Как правило, достаточно однокубитных (изменения состояний конкретного кубита) и каких-то двухкубитных запутывающих операций, которые создают корреляции между кубитами, поскольку любое преобразование n-кубитной системы можно представить в виде последовательности одно- и двухкубитных операций. Серия этих логических гейтов и есть программный код, который выполняет квантовый процессор.
- Требуется иметь возможность проводить вычисление достаточно быстро, пока квантовая система не потеряла когерентность или, наоборот, чтобы характерные времена когерентности физической системы были много больше, чем время выполнения логической операции, иначе длинную последовательность логических операций сделать не получится.
- И в конце нужно уметь считывать ответ, причем индивидуально с каждого кубита, ведь компьютер, с которым нельзя общаться, не очень интересная штука. Но, как правило, алгоритмы квантовых компьютеров вероятностные: вы необязательно видите ответ, но с большой вероятностью то, что вы увидите, будет близко к правильному ответу.
Ионы, атомы, фотоны, сверхпроводники: разные варианты физической архитектуры квантового компьютера
Ионы
Можно взять атом, например, щелочноземельного металла, удалить из него лишний электрон и сделать его заряженным ионом. Полученные частицы можно держать в специальных ионных ловушках при помощи радиочастотных полей: потенциалы на электродах очень быстро переключаются таким образом, чтобы создать устойчивое положение равновесия для иона. Таким способом люди умеют собирать из этих ионов цепочки и выстраивать их в кристалл, причем можно контролировать эту систему — например, менять расстояние между ионами. Расстояние можно подобрать таким образом, чтобы оно было, с одной стороны, не очень большим, чтобы удобно было раскачивать колебания в этой решетке, а с другой стороны, достаточно большим, чтобы можно было лазером посветить на отдельно взятый ион и управлять его квантовым состоянием. Первые квантовые гейты и были продемонстрированы именно в таких системах холодных ионов.
Атомы
Можно делать то же самое с нейтральными атомами. Поскольку они нейтральны, нужно использовать специальные оптические ловушки, например оптический пинцет — это сфокусированный лазерный луч, у которого в области перетяжки, где интенсивность максимальна, можно удерживать микрочастички. В такой оптический пинцет можно поместить буквально один атом и удерживать его там. Если вы создадите набор таких пинцетов, то получите вычислительный регистр, в котором у вас в каждом узле сидит по атому, которым вы до некоторой степени можете управлять.
Поскольку атомы не заряжены, то, когда они сидят в разных оптических пинцетах, они друг друга практически не чувствуют, а значит, их состояния не запутываются. Чтобы заставить атомы взаимодействовать на большом расстоянии, нужно отодвинуть электрон от ядра как можно дальше. И люди умеют это делать — это называется возбуждением ридберговских состояний. Ридберговский атом — это атом в состоянии с очень большим главным квантовым числом. Его проще всего представлять себе как атом, у которого валентный электрон болтается на очень далекой от ядра орбите, и она может быть настолько большой, что даже на расстоянии в несколько микронов атомы будут прекрасно чувствовать друг друга. Эти состояния достаточно долгоживущие, так что вы можете возбудить его туда, подождать некоторое время, пока соседние атомы взаимодействуют, и потом вернуть его обратно так, что при этом спонтанного излучения и потери когерентности не произойдет. С помощью возбуждения атомов в такие ридберговские состояния можно реализовывать взаимодействия контролируемым образом.
Сверхпроводники
Сверхпроводящие кубиты — это именно те кубиты, на которых работает большая часть коммерчески доступных квантовых процессоров. Компании Google и IBM сделали основную ставку именно на эту технологию, поскольку такие кубиты можно делать как электрические схемы, практически на печатной плате, только из сверхпроводящих материалов. Полученные процессоры охлаждаются до низких температур так, что металл, из которого они сделаны (это, как правило, алюминий), переходит в состояние сверхпроводимости. По сути такой кубит — это просто колебательный контур, который изучают в школе: конденсатор, катушка индуктивности, в нем ток и напряжение совершают колебания. Чтобы получить кубит, нужно добавить еще нелинейный элемент — так называемый джозефсоновский контакт.
Оказывается, если вы возьмете этот контур и охладите до очень низких температур, то увидите, что эти колебания проявляют квантовые свойства, но требуемая температура, как правило, хотя бы сотни милликельвинов. Причем, в отличие от атомов и ионов, здесь приходится охлаждать уже большую штуку, и для этого нужен настоящий большой холодильник, который действительно в самой глубокой стадии охлаждения имеет температуру, очень близкую к абсолютному нулю.
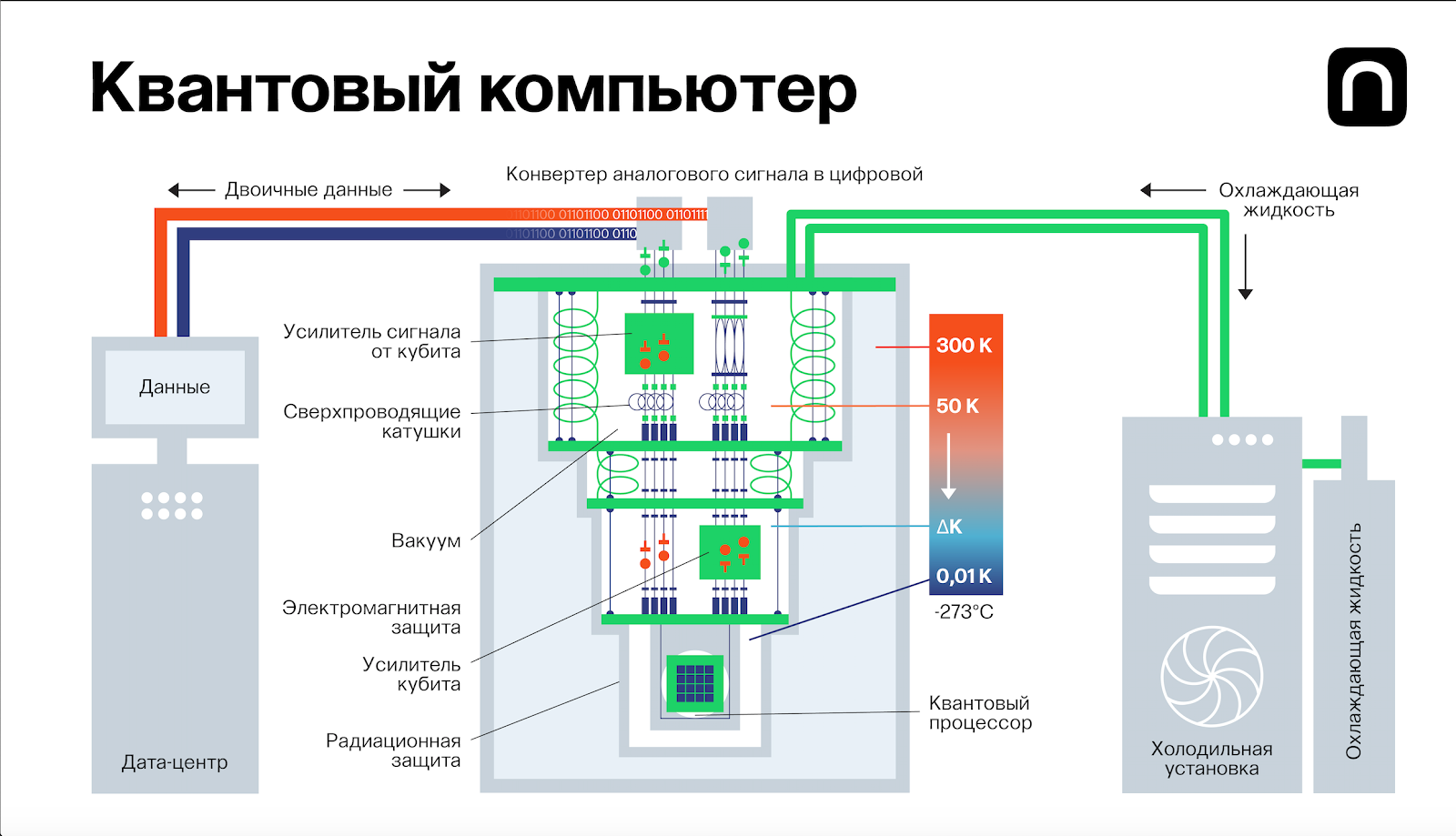
Екатерина Золотарёва для ПостНауки
Фотоны
Для квантовых компьютеров можно использовать фотоны — элементарные частички, из которых состоит электромагнитное излучение. Фотон является очень хорошим носителем квантовой информации, поскольку у каждого фотона есть свой естественный кубит — это поляризация. Свет, как известно, имеет два ортогональных состояния поляризации: горизонтальная и вертикальная (или правая и левая циркулярная). И эти два состояния — прекрасный логический базис для нашего кубита: у вас есть устройство для измерения, поляризатор, который можно крутить, таким образом выбирая базис в измерении, а свет либо проходит через него, либо нет.
Но с фотонами есть проблемы. Проблема первая и основная: фотоны между собой не очень взаимодействуют. Они электрически нейтральны и взаимодействовать напрямую не желают. Во многом это хорошо, потому что это дает практически полное отсутствие декогеренции: они не только между собой не взаимодействуют, но и с окружением тоже. С другой стороны, возникает проблема с двухкубитными операциями, потому что, раз они не взаимодействуют между собой, их и не запутать. Но оказывается, что есть трюки, которые позволяют это сделать ценой того, что мы отказываемся от детерминистической реализации этого запутывания: наши двухкубитные гейты становятся вероятностными, они иногда срабатывают, а иногда нет. Правда, они нас оповещают о том, сработали они или нет. И в результате вся последовательность операций в итоге приведет к вполне себе детерминистическому алгоритму. Но для этого требуются дополнительные фотоны. Поэтому вторая проблема, которая вытекает из первой: требуется очень много фотонов.
Проблемы и ограничения квантового компьютера
Дьявол, как обычно, в деталях — точнее, в числах. Реализовать логические операции с несколькими кубитами не очень сложно, но нужно их реализовать с дикой точностью: мы же не просто играемся с атомами — мы делаем компьютер, от которого хотим, чтобы по результатам большого количества операций получился ответ и он был правильный. Если прикинуть, какая точность должна быть у логических операций, чтобы после последовательного применения некоторого их количества получилось что-то осмысленное, окажется, что она должна быть очень большой: вероятности ошибки на уровне 10-5–10-6. Сделать логические операции с точностью в несколько процентов могут многие лаборатории, но вот сделать логические операции с точностью 10-5 не так просто. Это первая проблема.
Основная же проблема, с которой борются при создании квантовых компьютеров, — пресловутая потеря когерентности. Это неконтролируемое запутывание, которое происходит в вашей системе кубитов с окружением. То есть там вокруг тоже что-то есть, и за счет взаимодействия с этим окружением, которое вы не контролируете, происходит запутанность. Поскольку вы не мониторите это окружение, для вас это выглядит как ошибка — изменение состояния кубита, которое вы не контролируете. Проявляется это в шумах.
Будем ли мы использовать квантовые компьютеры вместо обычных?
Давайте предположим, что квантовый компьютер полностью эквивалентен классическому. Тогда классический должен уметь его моделировать: должна быть возможность написать программу для классического компьютера, которая будет делать все то же самое, что и квантовый. Для этого нам нужно будет взять математическое описание этой квантовой системы, которое в случае n кубитов — вектор из 2n чисел, и дальше с ним оперировать: умножать на матрицы. Размер этих матриц будет 2n х 2n. Это очень много, потому что для хранения действительного числа в памяти нужно много бит — например, 250 чисел уже не влезают даже в память терабайтных объемов. В результате получается, что прямой способ промоделировать квантово-механическую систему сталкивается с тем, что нам просто не хватает вычислительных ресурсов. Поэтому дизайнеры квантовых алгоритмов говорят: теперь этот логический аргумент повернем обратно; если у нас есть устройство, которое мы не можем промоделировать, значит, оно может решать вычислительные задачи, сложные для классического компьютера. На этом основана идея квантового превосходства. Оно было продемонстрировано недавно, в прошлом году, в реальном эксперименте инженерами компании Google на 53-кубитном процессоре.53 — это уже то число кубитов, которое превосходит возможности самых продвинутых суперкомпьютеров, существующих сейчас в мире. Все, что дальше, уже не моделируется классически.
Квантовый компьютер, с другой стороны, может полностью симулировать классический. Для этого достаточно просто запретить кубитам находиться в состоянии суперпозиции и разрешить им быть только нулями и единицами, и вы получаете набор битов, с помощью которого можно делать такие же вычисления, как на классическом компьютере. Собственно, в некотором смысле классический компьютер так и устроен, наш мир на фундаментальном уровне квантовый.
Какие задачи действительно осмысленно можно решать на квантовых компьютерах? Наверное, самый известный алгоритм для квантового компьютера — это алгоритм Шора. Он из области теории чисел и позволяет раскладывать числа на простые множители. Известно, что любое натуральное число единственным образом представимо в виде произведения простых чисел — это основная теорема арифметики, которую изучают в школе. Допустим, вы возьмете большое число, например число, которое в своей двоичной записи состоит из 256 бит, как ключи в системах шифрования, и вы знаете, что у него есть два простых сомножителя, из которых оно состоит. Надо определить из каких. Оказывается, что для этого нет эффективного алгоритма для классических компьютеров, то есть, увеличивая число бит в двоичной записи числа, вы увеличиваете сложность лучшего алгоритма, который может это сделать.
Но оказывается, что алгоритм Шора для квантового компьютера — способ решить данную задачу гораздо быстрее. Это важно, потому что сложность разложения на простые числа используется в современных криптографических алгоритмах. И когда стало понятно, что квантовый компьютер может делать это экспоненциально быстрее, чем классический, то люди, с одной стороны, заволновались, а с другой — возбудились, потому что это же приложение, которое интересно кому-то кроме физиков, занимающихся квантовыми вычислениями. Отсюда и стартовала вся эта квантовая гонка, попытка построить реальный квантовый компьютер.
Однако основные приложения сейчас видятся не в этом, а в физическом моделировании. Идея очень простая, она восходит еще к Фейнману, который в 1980-х годах высказал саму идею использования квантовых систем для моделирования ими других квантовых систем (одновременно с ним это сделал и Юрий Манин, наш соотечественник). Экспоненциальный рост размерности пространства состояний квантовой системы при увеличении числа частиц, которые в нее входят, — это проблема. Именно поэтому мы не можем из первых принципов моделировать большие молекулы вроде белков или твердотельные системы, которые состоят из огромного числа частиц. Они не поддаются моделированию, потому что не хватает вычислительных ресурсов, несмотря на то что мы знаем все фундаментальные законы, которые там действуют. Но можно взять другую квантовую систему (квантовый компьютер) и заставить ее считать. Эту идею можно воплотить в реальности если не сейчас, то уже в ближайшем будущем,причем даже десятков или сотен кубитов уже может быть достаточно, чтобы считать что-то, что невозможно посчитать на классическом компьютере.
Источник: postnauka.ru