Количественное сравнение между нейронной сетью и космической сетью

Мы исследуем сходство между двумя наиболее сложными и сложными системами в природе: сетью нейрональных клеток в человеческом мозге и космической сетью галактик. Мы исследуем структурные, морфологические, сетевые свойства и объем памяти этих двух увлекательных систем С помощью количественного подхода. Чтобы получить однородный анализ обеих систем, наша процедура рассматривает не истинную нейронную связность, а ее аппроксимацию, основанную на простой близости. Дразнящая степень сходства, которую выявляет наш анализ, по-видимому, предполагает, что самоорганизация обеих сложных систем, вероятно, формируется сходными принципами сетевой динамики, несмотря на радикально различные масштабы и процессы в игре.

Введение

Центральное место в нашем видении природы занимают две удивительные системы: сеть нейронов в человеческом мозге и космическая сеть галактик.

Человеческий мозг-это сложная во времени и пространстве многомасштабная структура, в которой сосуществуют клеточные, молекулярные и нейрональные явления. Он может быть смоделирован как иерархическая сеть (т. е. “коннектом человека” [1]), в которой нейроны группируются в схемы, столбцы и различные взаимосвязанные функциональные области. Структура нейронной сети позволяет устанавливать связи между различными областями, все они посвящены процессу специфической пространственно-временной деятельности над своими нейронами, образуя физическую и биологическую основу познания [напр., Ref. 2]. Некоторые из основных задач современной нейробиологии состоят в том, чтобы распутать структуру коннектома (например, полную карту нейронных связей в мозге), понять, как эта структура может производить сложные когнитивные функции, и определить роль глиальных клеток и микроокружения в физиологии межнейронных связей.

Вселенная, согласно обширной коллекции телескопических данных, собранных за многие десятилетия, по-видимому, достаточно хорошо описывается "консенсусной" физической моделью, называемой ?

Модель CDM (Lambda Cold Dark Matter), которая учитывает гравитацию от обычной и темной материи (т. е. очень слабо взаимодействующих частиц), для расширяющегося пространства-времени, описываемого Общей Теорией Относительности, и для антигравитационной энергии, связанной с пустым пространством, называемой “темной энергией”. Такая модель в настоящее время дает наилучшую картину того, как космические структуры возникли из расширяющегося фона и сформировали космическую паутину [например, Refs. 3 и 4]. Наиболее важными строительными блоками космической паутины являются самогравитирующиеся ореолы темной материи, в которых обычная материя коллапсирует, образуя галактики (и все звезды внутри них). Первоначальное распределение флуктуаций плотности материи было рано усилено действием гравитации и развилось в более крупные группы или скопления галактик, нитей, слоев материи и пустот, в крупномасштабную сеть во всех направлениях в пространстве. Среди основных проблем, с которыми все еще сталкивается космология, - физическая природа темной энергии, состав темной материи (или область альтернативных сценариев для нее), кажущаяся напряженность между различными измерениями скорости расширения Вселенной, точная последовательность процессов, ответственных за разнообразие морфологии галактик и их коэволюцию со сверхмассивными черными дырами. 5, для недавнего обзора].

Хотя соответствующие физические взаимодействия в вышеупомянутых двух системах совершенно различны, их наблюдение с помощью микроскопических и телескопических методов захватило дразнящую сходную морфологию, вплоть до того, что часто отмечалось, что космическая паутина и паутина нейронов выглядят одинаково [например, Refs. 6 и 7].

В этой работе мы применяем методы из космологии, нейробиологии и сетевого анализа, чтобы исследовать этот вызывающий мысль вопрос количественно впервые, к нашему знанию.

Материалы и методы

Иммуногистохимия и микроскопия

Мы проанализировали несколько независимых образцов церебральной и мозжечковой коры человека, которые были зафиксированы формалином и внедрены парафином [8], пробуя срезы глубины 4 ?m

, с коэффициентами увеличения 4x, 10x и 40x. Нейрофиламенты мечили с помощью моноклонального антитела мыши Neurofilament (2F11) (Ventana/CellMarque/Roche). Образцы автоматически обрабатывались Иммуностейнерами Ventana BenchMark Ultra. Затем для визуализации образцов был использован микроскоп Nikon eclipse 50i. Увеличение больше, чем 40x

было избегнуто для того чтобы получить более лучшее разрешение оптически глубины, так же, как уменьшить нелинейный ответ оптической микроскопии.

Космологическое Моделирование

Мы использовали синтетические образцы космической паутины с высоким разрешением (24003

клетки и частицы темной материи) моделирование кубического 1003 ПДК3 космический объем (1 ПДК=3,085?1024 см), выполненный с сеточным кодом ENZO [9], как подробно описано в Ref. 10. Моделирование дает реалистичное распределение темной материи, обычной материи и магнитных полей в настоящую эпоху. Чтобы имитировать процедуру "нарезания" тканей головного мозга, мы изготовили 12 различных тонких срезов (с толщиной 25 ПДК

) из моделируемого объема путем извлечения четырех срезов в перпендикулярных направлениях относительно каждой из независимых осей моделирования. Мы предоставляем публичный доступ к нашим космическим веб-изображениям, а также к образцам мозга и изображениям других природных сетей, обсуждаемых ниже по этому URL-адресу https://cosmosimfrazza.myfreesites.net/cosmic-web-and-brain-network-datasets.

Результаты

Абсолютные числа, внутренние пропорции и композиция

Сначала мы приводим данные, имеющиеся в литературе, которые позволяют нам провести первое поверхностное сравнение абсолютных размеров обеих систем. Радиус наблюдаемой Вселенной равен RU?13.9 Gpc

[11]. Экстраполяция последних наблюдений предполагает, что в общей сложности Ng~2.6?1012 галактики могут присутствовать в пределах сферы наблюдаемой Вселенной [12], причем до ~5?1010 галактики с массой, равной или большей массы Млечного Пути. Самые крупные скопления галактик имеют общую массу, превышающую 1015 солнечные массы (1 солнечная масса =1,989?1033 г

). Длинные нити обычной и темной материи протяженностью в несколько десятков Мегапарсеков соединяют скопления и группы галактик и разделены преимущественно пустым пространством [напр., Ref. 4].

По последним оценкам, мозг взрослого человека содержит Nneu?8.6±0.8?1010

всего нейронов и почти столько же не нейрональных клеток. Только ~20-25% из всех нейронов, расположенных в кортикальном сером веществе (представляющем собой ~80% процент массы мозга), в то время как мозжечок имеет около ~6.9?1010 нейроны (~80%

нейронов головного мозга) [13, 14].

Можно заметить, что эти две системы организованы в четко определенные сети, с ~1010-1011

узлы, соединенные между собой нитями (если рассматривать в качестве узлов все галактики с массами, сравнимыми или большими с массами Млечного Пути, см. выше), типичная протяженность которых составляет лишь крошечную долю (<=10-3) размера их хост-системы. Кроме того, галактики и нейроны имеют типичный масштабный радиус, который составляет лишь очень малую часть типичной длины нитей, с которыми они связаны. Более того, имеющиеся данные свидетельствуют о том, что поток информации и энергии в этих двух сетях в основном ограничен <=25%

о Массо-энергетическом содержании каждой системы.

В случае Вселенной мы имеем в виду современную композицию, основанную на сотрудничестве Планка и др. [15], так как относительное распределение энергии является функцией времени в ?

Космологическая модель CDM; для человеческого мозга мы ссылались на опубликованные исследования о составе человеческого мозга [например, Refs. 16 и 17].

Вкратце: 1) мозг состоит из воды (77-78%

), жир (10-12%), белковая пища (8%), углеводы (1%), растворимые органические вещества (2%), соль (1%2) Вселенная создана для того, чтобы 73~% темной энергией (скалярным энергетическим полем пустого пространства), для 22.5% темной материей, ибо 4.4% обычной барионной материей и менее чем за <=0.1%

фотонами и нейтрино.

Поразительно, что в обоих случаях ~75%

распределение массы / энергии состоит из явно пассивного материала, который пронизывает обе системы и играет лишь косвенную роль в их внутреннем строении: вода в случае мозга и темная энергия в космологии, которая в значительной степени не влияет на внутреннюю динамику космических структур [напр., Ref. 18].

Морфологическое Сравнение

Небольшие образцы коры головного мозга и мозжечка человека были собраны во время кортиэктомии, чтобы приблизиться к подкорковым опухолям (раздел 2.1). Затем нейрональные клетки окрашивали моноклональным антителом клона 2F11 против нейрофиламентов, которые представляют собой нейронспецифические промежуточные нити в цитоплазме нейронов, обеспечивающие структурную поддержку нейронального цитоскелета, наряду с микротрубочками и микрофиламентами. Было показано, что число, расстояние и площадная плотность нейрофиламентов в нейронах являются показателями с сильной зависимостью от калибра аксонов [например, Refs. 19–21]. Хотя плотность микротрубочек также зависит от калибра аксонов, было показано, что микротрубочки часто образуют небольшие скопления вблизи мембранозных органелл [22]. По этой причине мы считаем, что нейрофиламенты могут быть более однородно расположены в нейроне и, вероятно, будут лучшей мишенью для визуализации пространственного распределения нейронов в срезах. Для космической паутины мы проанализировали каждый из 12 тонких срезов из моделируемого объема (раздел 2.2), чтобы оценить влияние космической дисперсии. Такой 2-мерный подход имитирует то, что делается с образцами мозга, и из-за большой степени изотропии космической паутины на таких больших масштабах этот подход также может быть использован для быстрого перевода нашей статистики в 3-мерный случай.

На рис. 1 представлен обзор деталей структур, наблюдаемых в различных масштабах (от 4x

, 10x и 40x увеличения в случае мозговых тканей и на соответствующих этапах увеличения в случае космической паутины) в нашем наборе данных. Особенно на больших масштабах, различные образцы не показывают никакой впечатляющей степени сходства. В частности, преобладающая роль больших сверхплотностей, отмеченных скоплениями галактик, очевидна в образце космической паутины, в то время как более тонкая структура нейрофиламентов в образцах мозга производит более богатые мелкомасштабные паттерны. Однако при максимальном увеличении, достигаемом в наших мозговых срезах, утонченная сеть нейронных тел и нитей начинает представлять некоторое сходство с космической паутиной. <=20 ПДК

весы. При фокусировке на гистологических срезах можно заметить некоторую вариабельность, которая зависит от различных подтипов нейронов в коре головного мозга и мозжечка. На первом срезе показаны мелкие нейроны в зернистом слое, а также переход в ганглиарный слой с некоторыми клетками Пуркинье в нижней части рисунка. И наоборот, на втором срезе изображены крупные пирамидальные клетки, перемежающиеся с мелкими нейрональными клетками серого вещества мозга (зернистыми клетками).

Рисунок 1

Рисунок 1. Карты нормализованного контраста плотности, ??

например, срезы мозжечка (верхний ряд), коры головного мозга (средний ряд) и распределения темной материи в космической паутине (нижний ряд) для различных уровней увеличения. Спектральный и сетевой анализ, представленный в этой работе, будет в основном сосредоточен на 40x

образцы, как на правой панели.

Мы будем использовать в данной работе статистический инструментарий для 1) сравнения распределения структуры по всему континуальному диапазону пространственных масштабов наших выборок, также сравниваемых с другими природными сложными системами (раздел 3.3); 2) измерения свойств связности между узлами сети, оценивая тенденцию к образованию сильно кластеризованных конфигураций (см. раздел 3.4).

спектральный анализ

Мы использовали здесь статистику, обычно используемую в космологии: спектр мощности плотности, P(k)

, который непосредственно измеряет вклады различных пространственных частот, k=2?Л/Л (где l-пространственный масштаб, а L-максимальный масштаб каждой системы), к контрасту плотности, определяемому как ??=?/??-1, где ?-плотность и ?? это средняя плотность каждого образца. Мы измерили P(k) для наших 2-мерных образцов, путем разложения ?? в ряд дискретных пространственных частот, ?(k->): ??(k->)?(k?->)?=2?3P(k)?2D(k->+k?->), где ?2D

является 2-мерной Дельта-функцией Дирака.

В случае космологического моделирования, ???

она однозначно ограничена начальными условиями моделирования, в то время как в выборке коры головного мозга и мозжечка мы определяем ее на основе среднего значения, измеренного внутри самой выборки. Хотя точное знание контраста локальной плотности является тривиальным в моделировании, следует отметить, что точное отображение записанной интенсивности пикселей на проецируемую плотность материи далеко не тривиально в наблюдении под микроскопом из-за нелинейного отклика процесса микроскопического изображения. Как отмечалось в разделе 2.1, наш выбор заключается в использовании очень тонких образцов тканей и увеличении не более x40 это действительно мотивировано целью минимизации нелинейного отклика оптической микроскопии, сохраняя оптическую глубину небольшой по сравнению с апертурой изображения. По этой причине, ?? в образцах нашего мозга строго измеряется контраст оптических поглощений вдоль линии зрения, который мы принимаем за опосредованное значение плотностного контраста для сравнения с космологическими образцами. Мы применили стандартное быстрое преобразование Фурье с периодическими граничными условиями для вычисления спектров мощности образцов космической паутины (поскольку Домены действительно периодичны), в то время как в случае образцов мозга мы использовали стандартную технику заполнения нуля, чтобы встроить наблюдаемые образцы в 2x2

большая и пустая область, а также примененная аподизация на интерфейсах между пустой областью и данными, чтобы минимизировать паразитные краевые эффекты, как это обычно делается в моделировании [например, Ref. 23].

Полученные спектры мощности приведены на Рис .2. Следует подчеркнуть, что спектры мощности свободно скользят по горизонтали на графике в том смысле, что эталонная шкала L связана с k=1

решается a-posteriori. Далее, после предварительного сравнения спектров, мы скорректировали горизонтальную шкалу так, чтобы k=1 соответствовать L=1,6 мм в образцах мозга, и к L=100 ПДК в космической паутине. Это соответствует коэффициенту масштабирования 1.875?1027 между двумя системами. Амплитуда спектров в вертикальном направлении, напротив, самонормализуется до полной дисперсии ?? внутри каждого образца. Как следствие, образцы мозга по-разному нормализуются при k=1, так как при использовании меньшего увеличения и выборке больших пространственных масштабов, <=1.6 шкалы мм вносят пропорционально меньший вклад в дисперсию ?? в пределах всего образца. На первой панели мы сравниваем спектры случайного среза космической паутины со случайными срезами мозга, полученными при различных увеличениях. Сравнение поразительно показывает (в соответствии с тем, что было предложено на Рис. 1), что при сравнении получается замечательное сходство со спектрами <=1 мм шкалы в образцах мозга для <=100 ПДК-масштабы космической паутины. Большинство нейрональных клеток, наблюдаемых в наших мозжечковых образцах, представляют собой гранулярные клетки, причем соматы имеют ~5 ?m диаметр, в то время как их дендриты имеют дендриты с типичным ~13 ?m длина. Длина аксона (хотя и изменяется в зависимости от кортикальных областей) в среднем находится в диапазоне нескольких миллиметров [например, Ref. 24]. Учитывая, что срезы, используемые для микроскопического исследования, чаще всего не параллельны оси аксонов, вполне вероятно, что фрагменты этих волокон вокруг ~1-2 мм

по длине видны срезы. Таким образом, избыточная мощность спектров нейронной мощности в этом пространственном режиме отражает обилие структур с таким типичным распределением размеров.

Рисунок 2

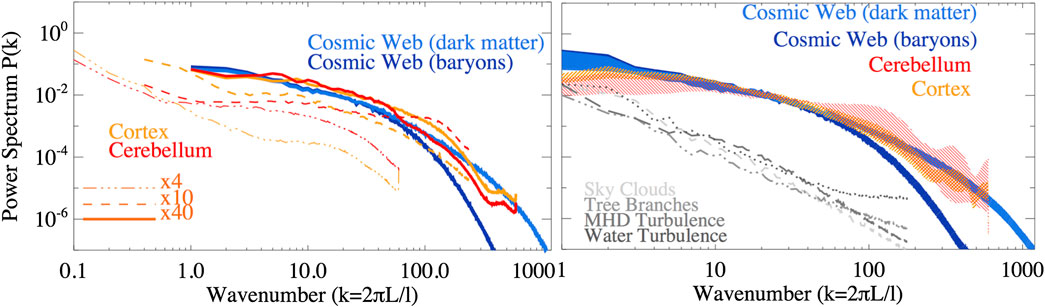
Рисунок 2. Слева: спектры мощности флуктуаций плотности во всех образцах (в случае образцов мозга показаны спектры от срезов разного размера и коэффициентов увеличения). Справа: спектры мощности флуктуаций плотности (в случае мозговых тканей только 40x

здесь используются срезы), с заштрихованными областями, охватывающими все распределение спектров для всех образцов (12 срезов для образцов космической паутины и четыре для образцов мозга). Сравнение спектров мощности от других образцов природных систем показано серыми линиями.

С другой стороны, колебания, измеряемые на >=1-2

мм-шкалы в образцах мозга имеют более крутую спектральную форму, чем в спектрах космической паутины. По этой причине в оставшейся части анализа мы сосредоточились на наборах данных о 40x образцы мозга для тщательного сравнения с кусочками космической паутины. На второй панели мы покажем P(k) как для темной материи, так и для газораспределения всех срезов, которые почти идентичны в больших масштабах (>= ПДК) и более диффузные в меньших масштабах за счет сглаживающего эффекта давления газа. Что касается спектров космической паутины, то мы показываем оболочку, содержащую все спектры всех 40x образцы с затененными участками. Мы находим большое соглашение почти по всему миру ~2 десятилетия в пространственных масштабах. Сходство между мозжечком на 0,01-1,6 мм масштабы и распределение темной материи космической паутины на 1-102 ПДК чешуя-это замечательно. В меньших масштабах образец коры демонстрирует значительно большую мощность, чем мозжечок, из-за распределения мелких нейронов в зернистом слое, описанном выше, в то время как распределение барионов космической паутины имеет меньшую мощность из-за (хорошо известного) эффекта давления газа в сглаживании флуктуаций плотности барионного газа в достаточно малом масштабе, чтобы гидродинамические эффекты были релевантны. Во всех случаях мы измеряем нарушенные степенные законы, в отличие от того, что ожидается для (более простых) фрактальных распределений [например, Ref. 25]. Это согласуется с несколькими работами, которые показали, что в небольших масштабах, r<=20 ПДК корреляционная функция галактики масштабируется следующим образом ?r-1

(где r-пространственный масштаб в 2-точечной корреляционной функции), в то время как на больших масштабах плотность лишь слабо (логарифмически) зависит от размера системы [например, Refs. 26 и 27].

Наконец, мы произвели спектры управляющей мощности для других случайно нарисованных образцов естественных сетей (облака неба, ветви деревьев, турбулентность воды и магнитогидродинамическая турбулентность- все это доступно по адресу https://cosmosimfrazza.myfreesites.net/cosmic-web-and-brain-network-datasets), с целью двойной проверки того, что наш метод не предвзят для получения сходства между действительно различными физическими системами. Как показано серыми линиями на правой панели рисунка 2 такие системы демонстрируют более регулярное степенное спектральное поведение, явно расходящееся с тем, что обнаруживается в основных сетях, анализируемых в этой работе, - даже если в последнем случае мы не проводили полного анализа во всем динамическом диапазоне таких систем, ища появление возможных спектральных признаков, как в случае мозга и космических образцов.

Однако спектры мощности слепы к фазовым корреляциям в непрерывном поле, поэтому два морфологически различных распределения все еще могут давать сходные спектры [28]. Таким образом, в следующем разделе мы также будем полагаться на неспектральные методы для сравнения различных выборок.

сетевой анализ

Сетевая наука распространилась на различные физические дисциплины, включая нейробиологию [например, Ref. 29-32], а также космологии [напр., Исх. 33 и 34]. Комплексный сетевой анализ может частично смягчить проблему отсутствия идеально согласованных оценок плотности в наших выборках в том смысле, что определение узлов различных сетей менее чувствительно к точным деталям отображения изображений. Мы сосредоточимся здесь на двух простых сетевых параметрах, обычно используемых в теории графов и сетевом анализе [например, Refs. 35 и 36]. Первый-это степень Централь-ности, Cd

, который измеряет степень связности сети в пределах локализованной области (определяется максимальной длиной связи, lссылка

):

Cd(j)=kjn-1(1)

где kj

это число (неориентированных) соединений с / из каждого j-узла, а n-общее число узлов во всей сети. Вторым параметром является коэффициент кластеризации C, который количественно определяет существование структуры в локальной окрестности узлов по сравнению с сетью случайных точек (т. е. отношение связанных треугольников узлов ко всем возможным тройкам в данном Связном кластере). Он измеряется как

C(j)=2yjkj(kj-1),(2)

в котором yj

это число связей между соседними узлами j-узла.

В то время как сложные методы идентификации узлов и нитей в моделируемой космической сети [например, Ref. 4] или в нейронной сети [например, Ref. 37] были предложены, здесь мы исследуем более простой подход с тем преимуществом, что он легко применим к обеим сетям. Этот метод вдохновлен стандартными процедурами” поиска гало " в космологии для идентификации самогравитирующих гало в космической паутине [38]. Подробно: 1) мы маркируем самые высокие пики интенсивности на всех картах (т. е. пикселы в верхней части 10%

распределения интенсивности каждой карты); 2) вычисляем вложенную среднюю интенсивность пикселей внутри окружностей возрастающего радиуса, пока не достигнем низкого порогового значения, ?, соответствует. Радиус окружности, достигающий ? значение определяет радиус каждого узла в сети (r?); 3) все пиксели на расстоянии <=r? предполагается, что они принадлежат этому узлу. В случае с космической паутиной мы адаптировали процедуру так, чтобы ?=330??, в то время как в случае мозговых сетей мы адаптировали значения ?

так что радиус узлов в сетях разумно соответствует размеру, предложенному визуальным осмотром.

Затем мы построили смежную матрицу узлов, Mij

, т. е. матрица со строками / столбцами, равными числу обнаруженных узлов, со значением Mij=1 если узлы разделены расстоянием <=Lссылка, или Mij=0 иначе. Выбор из lссылка произвольно, но полное сканирование параметров сети в зависимости от lссылка это выходит за рамки целей этой первой исследовательской работы. Таким образом, мы сосредоточились на одном конкретном выборе длины связи, мотивированном недавним анализом наблюдаемых галактик de Regt et al. [33], который предложил lссылка=1,2 ПДК в качестве эталонной " связующей длины” для ореолов материи в космической паутине (т. е., ~Л/100 на Рис. 2). Основываясь на сходстве спектров мощности после подходящей перенормировки пространственных масштабов, представленных в разделе 3.3, мы, таким образом, последовательно масштабировали длину связи в 40x образцы мозга, чтобы Lссылка=16 мкм

. На рис.3 крупным планом показаны узлы и сети, реконструированные для трех срезов нашего набора данных.

Рисунок 3

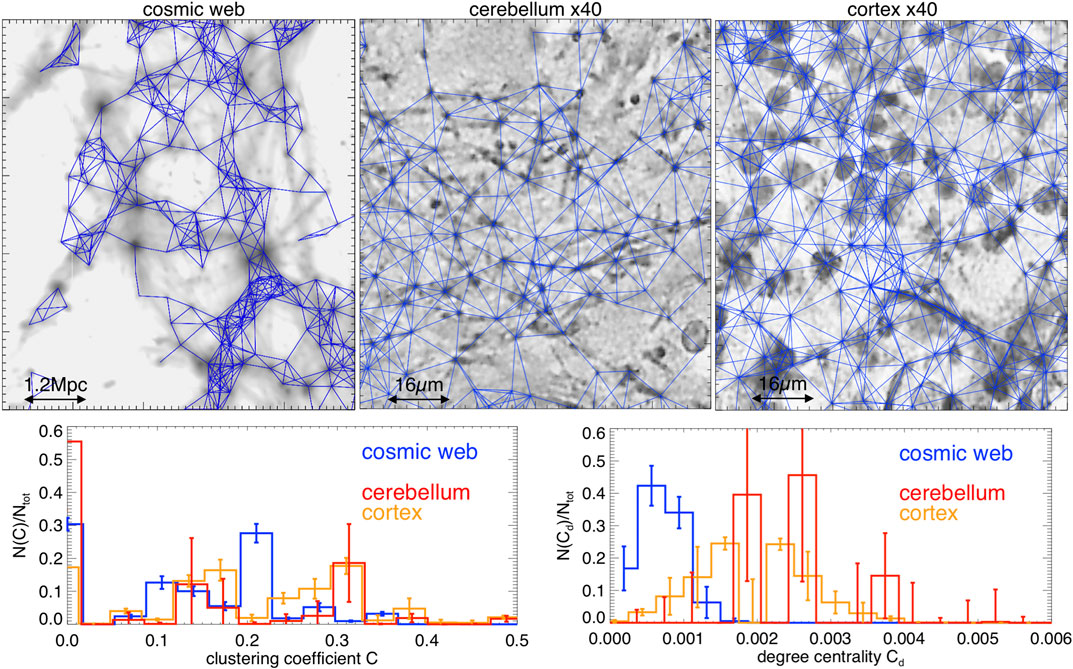
Рисунок 3. Верхние панели: увеличенные детали реконструированных соединений между узлами для трех примеров сетей в нашем примере (синие линии, наложенные на карты контрастности плотности). Нижние панели: распределения коэффициента кластеризации и степени централизации для всех срезов (полосы ошибок дают разброс внутри каждой исследуемой выборки срезов). Реконструированные связи не учитывают дальнодействующие нейронные связи,и показанные кластеры являются чисто пространственными.

Этот метод выбирает из N~3800-4700

узлы в наших космических срезах паутины, со средним числом ?k?~3.8-4.1 соединения на узел. Для срезов мозжечка мы измерили ?k1.91.9-3.7, в то время как для коры головного мозга мы измеряли ?k?~4.6-5.4 для N~1800-2000 идентифицированные узлы. С другой стороны, расчетное среднее число узлов для моделируемой космической сети равно ~40% меньший из результатов, полученных в ходе реальных исследований галактик de Regt et al. [33], что понятно из-за гораздо меньшей толщины наших модельных срезов (фактор ~4

тоньше в глубине комовинга по сравнению с наблюдениями).

Обе статистики ясно показывают, что сети мозга и космической паутины сильно отличаются от случайных сетей Эрдеша-Рени того же размера, которые вместо этого предсказывали бы для этих двух параметров Crandom??K?/N

(<=2?10-3 в нашем случае) и Cd,random?crandom(1-Crandom)/N (<=10-7-10-6 в нашем случае), в пределе большого N [например, Ref. 39]. Мы можем видеть, что вместо этого все измеренные распределения с измеряют несколько различных пиков в C~0.1-0.4 диапазон, ясно указывающий на то, что все сети сильно коррелированы, то есть их связи, как правило, сильно сгруппированы вместе. В случае космической паутины аналогичные разреженные пики были измерены в реальных данных de Regt et al. [33], и приписываются галактикам в умеренных количествах. (C?0,1) или богатый (C?0,3) среды, такие как нити накала или большие скопления галактик. Только остаточная часть распределений, с C<=10-2, вместо этого отмечает области сети, в которых связь близка к случайной (например, узлы в пустых областях). Сети также имеют значения степени Централь-ности, явно намного большие (на три-четыре порядка), чем соответствующие случайные сети. В космической сети распределяются Cd

являются приблизительно Пуассоновскими и соответствуют галактической сети, изученной Ref. 33, даже если пики распределения находятся на более низких значениях, чем образцы мозга. Последнее совместимо с усиленным присутствием мелких нейронов в зернистом слое, уже рассмотренным выше, что приводит к наличию более плотно упакованных кластеров узлов.

Отметим, что в данном исследовании мы проанализировали только часть коры головного мозга, а не всю центральную нервную систему, архитектура которой явно отличается. На самом деле, в то время как близость может точно описать космическую паутину, нейронные сети основаны на связях, и поэтому наш анализ не чувствителен к дальней связи. Но действительно, известно, что связь на большие расстояния является важнейшей особенностью нейронных сетей. Мы откладываем применение более сложной сетевой статистики [например, Ref. 40]) к будущей работе.

Обсуждение

Мы представили подробное сравнение между нейронной сетью и космической сетью, двумя самыми захватывающими и сложными сетями в природе, с целью объективной оценки уровня сходства между этими двумя физическими системами.

Мы также применили однородные статистические подходы к реальным лабораторным образцам как головного мозга, так и коры мозжечка (раздел 2.1), а также к срезам моделируемого распределения темной материи и обычного вещества в космической паутине (раздел 2.2) и количественно определили их морфологические и сетевые свойства с использованием спектрального анализа (раздел 3.3), а также сетевых параметров из теории графов (раздел 3.4). В рамках ряда упрощающих допущений, которые мы использовали для определения обеих сетей (например, на основе близости узлов, идентифицированных по непрерывному распределению материи, отображаемому различными методами визуализации), наши выводы намекают на то, что сходные конфигурации сетей могут возникать в результате взаимодействия совершенно разных физических процессов, приводящих к сходным уровням сложности и самоорганизации, несмотря на резкое неравенство в пространственных масштабах (т. е., ~1027

) из этих двух систем.

Мы понимаем, что этот подход имеет ряд ограничений. Во-первых, наше сравнение было сосредоточено на плотности материи. Выбор нейрофиламентов для очертания нейронной сети был основан на том, что они достаточно равномерно экспрессируются в цитоплазматическом компартменте нейронов. Наши результаты должны быть дополнительно подтверждены с помощью различных маркеров, таких как микрофиламенты или микротрубочки. Во-вторых, мы предположили, что наибольшая плотность пятен находится на уровне нейрональной сомы, что является аппроксимацией, приводящей к нестандартному определению узлов. Необходимы дальнейшие исследования, чтобы подтвердить наши результаты с помощью функциональных данных нейронной сети и без потери анатомо-визуального определения. В-третьих, наше исследование было основано на гистологических срезах, которые, очевидно, могут показать только крошечную часть самой мозговой сети. Более того, в то время как космическая сеть использует близость для определения своей сети, Нейронные сети основаны на связях, которые могут быть значительно дальнодействующими пространственно, и которые не могут быть должным образом оценены с помощью нашего анализа из-за технических ограничений метода. Из-за вышеуказанных ограничений мы не смогли представить систематический и полный анализ связности сетей, поскольку мы сосредоточились на простой близости, а не на дальней связности. Ключевым рубежом этого направления сравнительных исследований является возможность измерения объема памяти обеих сетей, задача, которая в настоящее время усложняется радикально различными подходами, доступными в настоящее время для измерения и мониторинга потока информации в них. Интересный факт хорошо иллюстрирует, что и в этом отношении возможны сходства. Общая емкость памяти человеческого мозга была недавно оценена с помощью секционной электронной микроскопии для реконструкции трехмерного распределения дендритных шипов и их синапсов, а также для обнаружения 26 различных синаптических сил, что составляет в среднем ~4.7

биты информации на нейрональную клетку [41]. Экстраполированный на общее среднее число узлов в нейронной сети, этот результат дает ?210 1016 бит, т. е., ~2.5 Петабайты - это объем памяти человеческого мозга. Для космической паутины можно использовать радикально иную идею, основанную на теории информации, чтобы количественно определить, сколько информации кодируется трехмерной структурой космической паутины [42, 43]. Путем вычисления "статистической сложности", характеризующей динамическую эволюцию моделируемых вселенных, было доказано, что ~3.5?1016 биты (т. е., ?4.3 Петабайты памяти) необходимы для хранения информации о космической структуре во всей наблюдаемой Вселенной (?13.8 Gpc

). Такое близкое совпадение может показаться простым совпадением, учитывая, что, учитывая неоднозначность определения обеих сетей, в частности космической паутины, эти числа известны лишь приблизительно.

Вместе с остальной частью анализа, представленного в этой работе, такие сходства призваны мотивировать разработку более мощных и различающих алгоритмов для определения аналогий и различий этих захватывающих систем, почти на мыслимых крайностях пространственных масштабов во Вселенной.

Источник: www.frontiersin.org

Комментарии: