Пишем нейросеть на Python с нуля

Статья публикуется в переводе, автор оригинального текста Victor Zhou.

***

Пишем нейросеть на Python с нуля

Термин "нейронные сети" сейчас можно услышать из каждого утюга, и многие верят, будто это что-то очень сложное. На самом деле нейронные сети совсем не такие сложные, как может показаться! Мы разберемся, как они работают, реализовав одну сеть с нуля на Python.

Эта статья предназначена для полных новичков, не имеющих никакого опыта в машинном обучении. Поехали!

1. Составные элементы: нейроны

Прежде всего нам придется обсудить нейроны, базовые элементы нейронной сети. Нейрон принимает несколько входов, выполняет над ними кое-какие математические операции, а потом выдает один выход. Вот как выглядит нейрон с двумя входами:

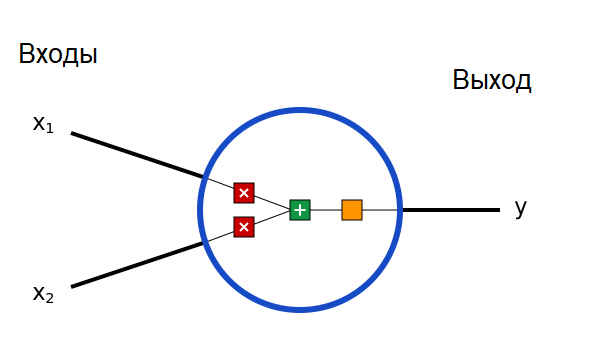
Внутри нейрона происходят три операции. Сначала значения входов умножаются на веса:

$$x_1?x_1?w_1,x_2?x_2?w_2$$

Затем взвешенные входы складываются, и к ним прибавляется значение порога b:

$$x_1?w_1+x_2?w_2+b$$

Наконец, полученная сумма проходит через функцию активации:

$$у=f(x_1?w_1+x_2?w_2+b)$$

Функция активации преобразует неограниченные значения входов в выход, имеющий ясную и предсказуемую форму. Одна из часто используемых функций активации – сигмоида:

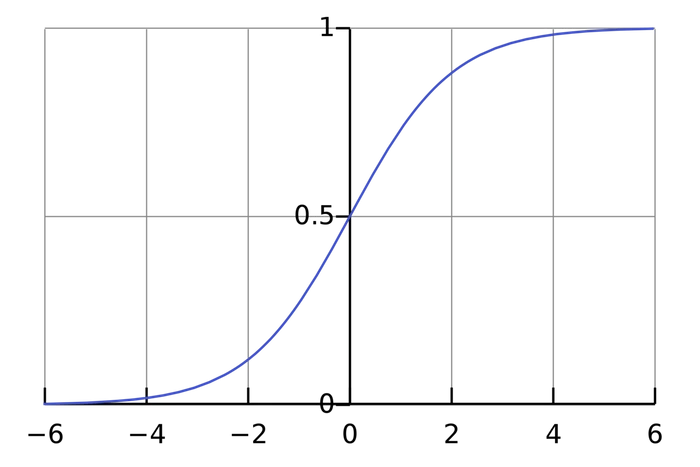
Сигмоида выдает результаты в интервале (0, 1). Можно представить, что она «упаковывает» интервал от минус бесконечности до плюс бесконечности в (0, 1): большие отрицательные числа превращаются в числа, близкие к 0, а большие положительные – к 1.

Простой пример

Допустим, наш двухвходовой нейрон использует сигмоидную функцию активации и имеет следующие параметры:

$$w=[0,1]b=4$$

w=[0, 1] – это всего лишь запись w₁=0, w₂=1 в векторном виде. Теперь зададим нашему нейрону входные данные: x=[2, 3]. Мы используем скалярное произведение векторов, чтобы записать формулу в сжатом виде:

$$(w?x)+b=((w_1?x_1)+(w_2?x_2))+b=0?2+1?3+4=7$$

$$y=f(w?x+b)=f(7)=0.999$$

Наш нейрон выдал 0.999 при входах x=[2, 3]. Вот и все! Процесс передачи значений входов дальше, чтобы получить выход, называется прямой связью (feed forward).

Пишем код для нейрона

Настало время написать свой нейрон! Мы используем NumPy, популярную и мощную расчетную библиотеку для Python, которая поможет нам с вычислениями:

         import numpy as np  def sigmoid(x):   # Наша функция активации: f(x) = 1 / (1 + e^(-x))   return 1 / (1 + np.exp(-x))  class Neuron:   def __init__(self, weights, bias):     self.weights = weights     self.bias = bias    def feedforward(self, inputs):     # Умножаем входы на веса, прибавляем порог, затем используем функцию активации     total = np.dot(self.weights, inputs) + self.bias     return sigmoid(total)  weights = np.array([0, 1]) # w1 = 0, w2 = 1 bias = 4                   # b = 4 n = Neuron(weights, bias)  x = np.array([2, 3])       # x1 = 2, x2 = 3 print(n.feedforward(x))    # 0.9990889488055994     

Узнаете эти числа? Это тот самый пример, который мы только что рассчитали! И мы получили тот же результат – 0.999.

2. Собираем нейронную сеть из нейронов

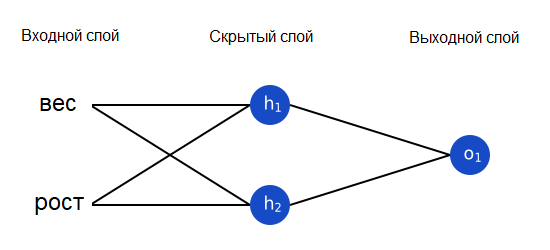
Нейронная сеть – это всего лишь несколько нейронов, соединенных вместе. Вот как может выглядеть простая нейронная сеть:

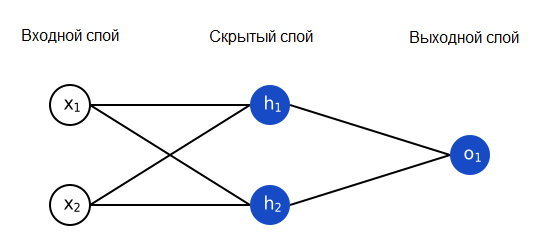
У этой сети два входа, скрытый слой с двумя нейронами (h₁ и h₂) и выходной слой с одним нейроном (o₁). Обратите внимание, что входы для o₁ – это выходы из h₁ и h₂. Именно это создает из нейронов сеть.

Пример: прямая связь

Давайте используем сеть, изображенную выше, и будем считать, что все нейроны имеют одинаковые веса w=[0, 1], одинаковые пороговые значения b=0, и одинаковую функцию активации – сигмоиду. Пусть h₁, h₂ и o₁ обозначают выходные значения соответствующих нейронов.

Что получится, если мы подадим на вход x=[2, 3]?

$$\begin{array}{rl}& h_1=h_2=f(w?x+b)=f((0?2)+(1?3)+0)=f(3)=0.9526\\ & o_1=f(w?[h_1,h_2]+b)=f((0?h_1)+(1?h_2)+0)=f(0.9526)=\mathbf{\text{0.7216}}\end{array}$$

Если подать на вход нашей нейронной сети x=[2, 3], на выходе получится 0.7216. Достаточно просто, не правда ли?

Нейронная сеть может иметь любое количество слоев, и в этих слоях может быть любое количество нейронов. Основная идея остается той же: передавайте входные данные по нейронам сети, пока не получите выходные значения. Для простоты мы будем использовать сеть, показанную выше, до конца статьи.

Пишем код нейронной сети

Давайте реализуем прямую связь для нашей нейронной сети. Напомним, как она выглядит:

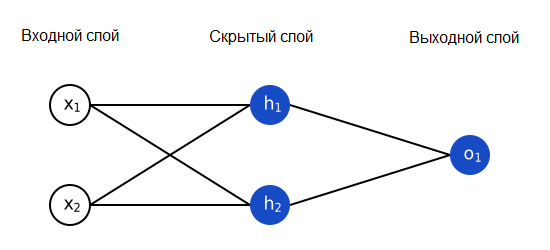
         import numpy as np  # ... вставьте сюда код из предыдущего раздела  class OurNeuralNetwork:   '''   Нейронная сеть с:     - 2 входами     - скрытым слоем с 2 нейронами (h1, h2)     - выходным слоем с 1 нейроном (o1)   Все нейроны имеют одинаковые веса и пороги:     - w = [0, 1]     - b = 0   '''   def __init__(self):     weights = np.array([0, 1])     bias = 0      # Используем класс Neuron из предыдущего раздела     self.h1 = Neuron(weights, bias)     self.h2 = Neuron(weights, bias)     self.o1 = Neuron(weights, bias)    def feedforward(self, x):     out_h1 = self.h1.feedforward(x)     out_h2 = self.h2.feedforward(x)      # Входы для o1 - это выходы h1 и h2     out_o1 = self.o1.feedforward(np.array([out_h1, out_h2]))      return out_o1  network = OurNeuralNetwork() x = np.array([2, 3]) print(network.feedforward(x)) # 0.7216325609518421     

Мы снова получили 0.7216! Похоже, наша сеть работает.

3. Обучаем нейронную сеть (часть 1)

Допустим, у нас есть следующие измерения:

Давайте обучим нашу нейронную сеть предсказывать пол человека по его росту и весу.

Мы будем представлять мужской пол как 0, женский – как 1, а также сдвинем данные, чтобы их было проще использовать:

Потери

Прежде чем обучать нашу нейронную сеть, нам нужно как-то измерить, насколько "хорошо" она работает, чтобы она смогла работать "лучше". Это измерение и есть потери (loss).

Мы используем для расчета потерь среднюю квадратичную ошибку (mean squared error, MSE):

$$MSE=\frac{1}{n}\underset{i=1}{\overset{n}{?}}(y_{true}?y_{pred}{)}^2$$

Давайте рассмотрим все используемые переменные:

• n – это количество измерений, в нашем случае 4 (Алиса, Боб, Чарли и Диана).
• y представляет предсказываемое значение, Пол.
• y_true – истинное значение переменной ("правильный ответ"). Например, для Алисы y_true будет равна 1 (женский пол).
• y_pred – предсказанное значение переменной. Это то, что выдаст наша нейронная сеть.

(y_true-y_pred)² называется квадратичной ошибкой. Наша функция потерь просто берет среднее значение всех квадратичных ошибок – поэтому она и называется средней квадратичной ошибкой. Чем лучшими будут наши предсказания, тем меньшими будут наши потери!

Лучшие предсказания = меньшие потери.

Обучение нейронной сети = минимизация ее потерь.

Пример расчета потерь

Предположим, что наша сеть всегда возвращает 0 – иными словами, она уверена, что все люди мужчины. Насколько велики будут наши потери?

$$MSE=\frac{1}{4}(1+0+0+1)=0.5$$

Пишем функцию средней квадратичной ошибки

Вот небольшой кусок кода, который рассчитает наши потери. Если вы не понимаете, почему он работает, прочитайте в руководстве NumPy про операции с массивами.

         import numpy as np  def mse_loss(y_true, y_pred):   # y_true и y_pred - массивы numpy одинаковой длины.   return ((y_true - y_pred) ** 2).mean()  y_true = np.array([1, 0, 0, 1]) y_pred = np.array([0, 0, 0, 0])  print(mse_loss(y_true, y_pred)) # 0.5     

Отлично. Идем дальше!

4. Обучаем нейронную сеть (часть 2)

Теперь у нас есть четкая цель: минимизировать потери нейронной сети. Мы знаем, что можем изменять веса и пороги нейронов, чтобы изменить ее предсказания, но как нам делать это таким образом, чтобы минимизировать потери?

Для простоты давайте представим, что в нашем наборе данных только одна Алиса.

Тогда средняя квадратичная ошибка будет квадратичной ошибкой только для Алисы:

$$MSE=\frac{1}{1}\underset{i=1}{\overset{1}{?}}(y_{true}?y_{pred}{)}^2=(y_{true}?y_{pred}{)}^2=(1?y_{pred}{)}^2$$

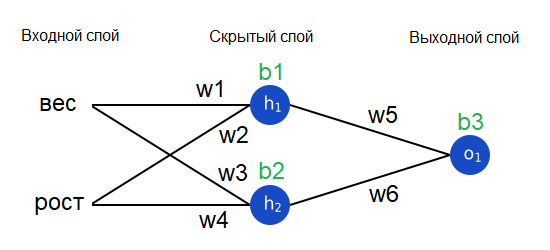
Другой метод – это рассматривать функцию потерь как функцию от весов и порогов. Давайте отметим все веса и пороги нашей нейронной сети:

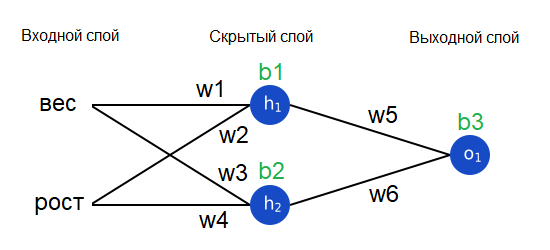
Теперь мы можем записать функцию потерь как функцию от нескольких переменных:

$$L(w_1,w_2,w_3,w_4,w_5,w_6,b_1,b_2,b_3)$$

Предположим, мы хотим отрегулировать w₁. Как изменится значение потери L при изменении w₁? На этот вопрос может ответить частная производная dL/dw₁. Как мы ее рассчитаем?

Прежде всего, давайте перепишем эту частную производную через dy_pred/dw₁, воспользовавшись цепным правилом:

$$\frac{\mathrm{?}L}{\mathrm{?}{w}_1}=\frac{\mathrm{?}L}{\mathrm{?}{y}_{pred}}?\frac{\mathrm{?}{y}_{pred}}{\mathrm{?}{w}_1}$$

Мы можем рассчитать dL/d_ypred, поскольку мы уже выяснили выше, что L=(1-y_pred)²:

$$\frac{\mathrm{?}L}{\mathrm{?}{y}_{pred}}=\frac{\mathrm{?}(1?y_{pred}{)}^2}{\mathrm{?}{y}_{pred}}=\boxed{{\displaystyle ?2(1?y_{pred})}}$$

Теперь давайте решим, что делать с dy_pred/dw₁. Обозначая выходы нейронов, как прежде, h₁, h₂ и o₁, получаем:

$$y_{pred}=o_1=f(w_5{h}_1+w_6{h}_2+b_3)$$

Вспомните, что f() – это наша функция активации, сигмоида. Поскольку w₁ влияет только на h₁ (но не на h₂), мы можем снова использовать цепное правило и записать:

$$\begin{array}{rl}& \frac{\mathrm{?}{y}_{pred}}{\mathrm{?}{w}_1}=\frac{\mathrm{?}{y}_{pred}}{\mathrm{?}{h}_1}?\frac{\mathrm{?}{h}_1}{\mathrm{?}{w}_1}\\ & \frac{\mathrm{?}{y}_{pred}}{\mathrm{?}{h}_1}=\boxed{{\displaystyle w_5?f\mathrm{?}(w_5{h}_1+w_6{h}_2+b_3)}}\end{array}$$

Мы можем сделать то же самое для dh₁/dw₁, снова применяя цепное правило:

$$\begin{array}{rl}& h_1=f(w_1{x}_1+w_2{x}_2+b_1)\\ & \frac{\mathrm{?}{h}_1}{\mathrm{?}{w}_1}=\boxed{{\displaystyle x_1?f\mathrm{?}(w_1{x}_1+w_2{x}_2+b_1)}}\end{array}$$

В этой формуле x₁ – это вес, а x₂ – рост. Вот уже второй раз мы встречаем f'(x) – производную сигмоидной функции! Давайте вычислим ее:

$$\begin{array}{cc}& f(x)=\frac{1}{1+e^{?x}}\\ & f\mathrm{?}(x)=\frac{e^{?x}}{(1+e^{?x}{)}^2}=f(x)?(1?f(x))\end{array}$$

Мы используем эту красивую форму для f'(x) позже. На этом мы закончили! Мы сумели разложить dL/dw₁ на несколько частей, которые мы можем рассчитать:

$$\boxed{{\displaystyle \frac{\mathrm{?}L}{\mathrm{?}{w}_1}=\frac{\mathrm{?}L}{\mathrm{?}{y}_{pred}}?\frac{\mathrm{?}{y}_{pred}}{\mathrm{?}{h}_1}?\frac{\mathrm{?}{h}_1}{\mathrm{?}{w}_1}}}$$

Такой метод расчета частных производных "от конца к началу" называется методом обратного распространения (backpropagation).

Уффф. Здесь было очень много символов, так что не страшно, если вы пока не все понимаете. Давайте покажем, как это работает, на практическом примере!

Пример. Считаем частную производную

Мы по-прежнему считаем, что наш набор данных состоит из одной Алисы:

Давайте инициализируем все веса как 1, а все пороги как 0. Если мы выполним прямой проход по нейронной сети, то получим:

$$\begin{array}{rl}& h_1=f(w_1{x}_1+w_2{x}_2+b_1)=f(?2+(?1)+0)=0.0474\\ & h_2=f(w_3{x}_1+w_4{x}_2+b_2)=0.0474\\ & o_1=f(w_5{h}_1+w_6{h}_2+b_3)=f(0.0474+0.0474+0)=0.524\end{array}$$

Наша сеть выдает y_pred=0.524, что находится примерно на полпути между Мужским полом (0) и Женским (1). Давайте рассчитаем dL/dw₁:

$$\begin{array}{rl}& \frac{\mathrm{?}L}{\mathrm{?}{w}_1}=\frac{\mathrm{?}L}{\mathrm{?}{y}_{pred}}?\frac{\mathrm{?}{y}_{pred}}{\mathrm{?}{h}_1}?\frac{\mathrm{?}{h}_1}{\mathrm{?}{w}_1}\\ & \frac{\mathrm{?}L}{\mathrm{?}{y}_{pred}}=?2(1?y_{pred})=?2(1?0.524)=?0.952\\ & \frac{\mathrm{?}{y}_{pred}}{\mathrm{?}{h}_1}=w_5?f\mathrm{?}(w_5{h}_1+w_6{h}_2+b_3)=1?f\mathrm{?}(0.0474+0.0474+0)=f(0.948)(1?f(0.948))=0.249\\ & \frac{\mathrm{?}{h}_1}{\mathrm{?}{w}_1}=x_1?f\mathrm{?}(w_1{x}_1+w_2{x}_2+b_1)=?2?f\mathrm{?}(?2+(?1)+0)=?2?f(?3)?(1?f(?3))=?0.0904\\ & \frac{\mathrm{?}L}{\mathrm{?}{w}_1}=?0.952?0.249??0.0904=0.0214\end{array}$$

Вот и все! Результат говорит нам, что при увеличении w_1, функция ошибки чуть-чуть повышается.

Обучение: стохастический градиентный спуск

Теперь у нас есть все нужные инструменты для обучения нейронной сети! Мы используем алгоритм оптимизации под названием стохастический градиентный спуск (stochastic gradient descent), который определит, как мы будем изменять наши веса и пороги для минимизации потерь. Фактически, он заключается в следующей формуле обновления:

$$\begin{array}{rl}& w_1?w_1??\frac{\mathrm{?}L}{\mathrm{?}{w}_1}\\ & ?(eta)?константа,называемая\mathbf{\text{скоростью}}\mathbf{\text{обучения}}(learningrate).\end{array}$$

Скорость обучения определяет, как быстро наша сеть учится. Все, что мы делаем – это вычитаем eta*dL/dw₁ из w₁:

• Если dL/dw₁ положительна, w₁ уменьшится, что уменьшит L.
• Если dL/dw₁ отрицательна, w₁ увеличится, что также уменьшит L.

Если мы сделаем то же самое для каждого веса и порога в сети, потери будут постепенно уменьшаться, и наша сеть будет выдавать более точные результаты.

Процесс обучения сети будет выглядеть примерно так:

1. Выбираем одно наблюдение из набора данных. Именно то, что мы работаем только с одним наблюдением, делает наш градиентный спуск стохастическим.
2. Считаем все частные производные функции потерь по всем весам и порогам (dL/dw₁, dL/dw₂ и т.д.)
3. Используем формулу обновления, чтобы обновить значения каждого веса и порога.
4. Снова переходим к шагу 1.

Пишем код всей нейронной сети

Наконец настало время реализовать всю нейронную сеть.

         import numpy as np  def sigmoid(x):   # Сигмоидная функция активации: f(x) = 1 / (1 + e^(-x))   return 1 / (1 + np.exp(-x))  def deriv_sigmoid(x):   # Производная сигмоиды: f'(x) = f(x) * (1 - f(x))   fx = sigmoid(x)   return fx * (1 - fx)  def mse_loss(y_true, y_pred):   # y_true и y_pred - массивы numpy одинаковой длины.   return ((y_true - y_pred) ** 2).mean()  class OurNeuralNetwork:   '''   Нейронная сеть с:     - 2 входами     - скрытым слоем с 2 нейронами (h1, h2)     - выходной слой с 1 нейроном (o1)    *** DISCLAIMER ***:   Следующий код простой и обучающий, но НЕ оптимальный.   Код реальных нейронных сетей совсем на него не похож. НЕ копируйте его!    Изучайте и запускайте его, чтобы понять, как работает эта нейронная сеть.   '''   def __init__(self):     # Веса     self.w1 = np.random.normal()     self.w2 = np.random.normal()     self.w3 = np.random.normal()     self.w4 = np.random.normal()     self.w5 = np.random.normal()     self.w6 = np.random.normal()      # Пороги     self.b1 = np.random.normal()     self.b2 = np.random.normal()     self.b3 = np.random.normal()    def feedforward(self, x):     # x is a numpy array with 2 elements.     h1 = sigmoid(self.w1 * x[0] + self.w2 * x[1] + self.b1)     h2 = sigmoid(self.w3 * x[0] + self.w4 * x[1] + self.b2)     o1 = sigmoid(self.w5 * h1 + self.w6 * h2 + self.b3)     return o1    def train(self, data, all_y_trues):     '''     - data - массив numpy (n x 2) numpy, n = к-во наблюдений в наборе.      - all_y_trues - массив numpy с n элементами.       Элементы all_y_trues соответствуют наблюдениям в data.     '''     learn_rate = 0.1     epochs = 1000 # сколько раз пройти по всему набору данных       for epoch in range(epochs):       for x, y_true in zip(data, all_y_trues):         # --- Прямой проход (эти значения нам понадобятся позже)         sum_h1 = self.w1 * x[0] + self.w2 * x[1] + self.b1         h1 = sigmoid(sum_h1)          sum_h2 = self.w3 * x[0] + self.w4 * x[1] + self.b2         h2 = sigmoid(sum_h2)          sum_o1 = self.w5 * h1 + self.w6 * h2 + self.b3         o1 = sigmoid(sum_o1)         y_pred = o1          # --- Считаем частные производные.         # --- Имена: d_L_d_w1 = "частная производная L по w1"         d_L_d_ypred = -2 * (y_true - y_pred)          # Нейрон o1         d_ypred_d_w5 = h1 * deriv_sigmoid(sum_o1)         d_ypred_d_w6 = h2 * deriv_sigmoid(sum_o1)         d_ypred_d_b3 = deriv_sigmoid(sum_o1)          d_ypred_d_h1 = self.w5 * deriv_sigmoid(sum_o1)         d_ypred_d_h2 = self.w6 * deriv_sigmoid(sum_o1)          # Нейрон h1         d_h1_d_w1 = x[0] * deriv_sigmoid(sum_h1)         d_h1_d_w2 = x[1] * deriv_sigmoid(sum_h1)         d_h1_d_b1 = deriv_sigmoid(sum_h1)          # Нейрон h2         d_h2_d_w3 = x[0] * deriv_sigmoid(sum_h2)         d_h2_d_w4 = x[1] * deriv_sigmoid(sum_h2)         d_h2_d_b2 = deriv_sigmoid(sum_h2)          # --- Обновляем веса и пороги         # Нейрон h1         self.w1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w1         self.w2 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_w2         self.b1 -= learn_rate * d_L_d_ypred * d_ypred_d_h1 * d_h1_d_b1          # Нейрон h2         self.w3 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w3         self.w4 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_w4         self.b2 -= learn_rate * d_L_d_ypred * d_ypred_d_h2 * d_h2_d_b2          # Нейрон o1         self.w5 -= learn_rate * d_L_d_ypred * d_ypred_d_w5         self.w6 -= learn_rate * d_L_d_ypred * d_ypred_d_w6         self.b3 -= learn_rate * d_L_d_ypred * d_ypred_d_b3        # --- Считаем полные потери в конце каждой эпохи       if epoch % 10 == 0:         y_preds = np.apply_along_axis(self.feedforward, 1, data)         loss = mse_loss(all_y_trues, y_preds)         print("Epoch %d loss: %.3f" % (epoch, loss))  # Определим набор данных data = np.array([   [-2, -1],  # Алиса   [25, 6],   # Боб   [17, 4],   # Чарли   [-15, -6], # Диана ]) all_y_trues = np.array([   1, # Алиса   0, # Боб   0, # Чарли   1, # Диана ])  # Обучаем нашу нейронную сеть! network = OurNeuralNetwork() network.train(data, all_y_trues)     

По мере обучения сети ее потери постепенно уменьшаются:

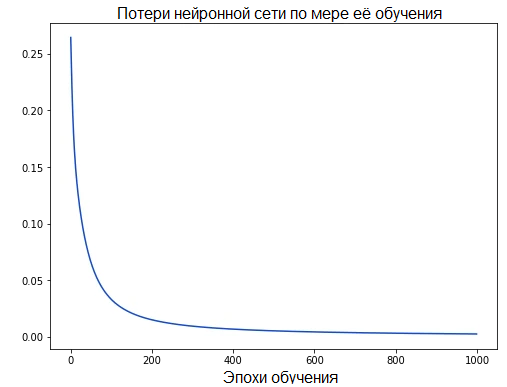
Теперь мы можем использовать нашу сеть для предсказания пола:

         # Делаем пару предсказаний emily = np.array([-7, -3]) # 128 фунтов (52.35 кг), 63 дюйма (160 см) frank = np.array([20, 2])  # 155 pounds (63.4 кг), 68 inches (173 см) print("Эмили: %.3f" % network.feedforward(emily)) # 0.951 - Ж print("Фрэнк: %.3f" % network.feedforward(frank)) # 0.039 - М     

Что теперь?

Вы сделали это! Давайте перечислим все, что мы с вами сделали:

• Определили нейроны, составные элементы нейронных сетей.
• Использовали сигмоидную функцию активации для наших нейронов.
• Увидели, что нейронные сети – это всего лишь несколько нейронов, соединенных друг с другом.
• Создали набор данных, в котором Вес и Рост были входными данными (или признаками), а Пол – выходным (или меткой).
• Узнали о функции потерь и средней квадратичной ошибке (MSE).
• Поняли, что обучение нейронной сети – это всего лишь минимизация ее потерь.
• Использовали метод обратного распространения (backpropagation) для расчета частных производных.
• Использовали стохастический градиентный спуск (SGD) для обучения нашей сети.

Перед вами – множество путей, на которых вас ждет масса нового и интересного:

• Экспериментируйте с большими и лучшими нейронными сетями, используя подходящие библиотеки вроде Tensorflow, Keras и PyTorch.
• Создайте свою первую нейронную сеть с помощью Keras.
• Прочитайте остальные статьи из серии "Нейронные сети с нуля".
• Исследуйте другие функции активации, кроме сигмоиды, например, Softmax.
• Исследуйте другие оптимизаторы, кроме стохастического градиентного спуска.

Спасибо за внимание!