Исследование устойчивости сверточных нейросетей. Часть 1: Теория

МЕНЮ

Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту

ТЕМЫ

Новости ИИРазработка ИИВнедрение ИИРабота разума и сознаниеМодель мозгаРобототехника, БПЛАТрансгуманизмОбработка текстаТеория эволюцииДополненная реальностьЖелезоКиберугрозыНаучный мирИТ индустрияРазработка ПОТеория информацииМатематикаЦифровая экономика

Авторизация

RSS

RSS новости
Если Вам интересно разобраться, насколько современные (прежде всего, сверточные) нейросети устойчивы, насколько легко можно менять их выход небольшим искажением входных данных, а также возможно ли это делать на уровне реальных (физических) атрибутов объектов перед их съемкой на (фото)видеокамеру — милости просим под кат!

Введение в сверточные нейронные сети

Начиная с 1943 года, когда впервые была предложена математическая формализация МакКалоком и Питтсом понятия «искусственного нейрона», нейросети становились:

  • Объемнее (содержали больше параметров),
  • Глубже (содержали больше блоков вычислений),
  • Лучше! (более правильно решали поставленные перед ними задачи)

image
На данный момент ни для кого уже не секрет, что для работы с фотографиями и видео лучше всего подходят сверточные нейронные сети (СНС), которые, например, позволяют выделять объекты и определять их класс, да и, наконец, отвечают на недавний главный вопрос компьютерного зрения – кошка или собака (серьезная ссылка и несерьезная ссылка по теме)? И все же, так ли уж хороши сверточные нейросети, действительно ли оправдано все то внимание, которое им уделяют? Попробуем разбить на два подвопроса:

  1. Как сейчас соотносится качество распознавания человеком и СНС для известных баз данных?
  2. Насколько устойчивы СНС по отношению к входным данным? Легко ли их сломать?

Прогресс в сверточных нейронных сетях

Для ответа на первый вопрос обратимся к двум популярным базам данных изображений — ImageNet (1000-классовая база данных изображений) и Labeled Faces in the Wild (LFW) (база данных лиц).

Примеры изображений
ImageNet:
LFW:
Итак, классификация на ImageNet:
  • Top-5 ошибка (вероятность того, что правильный класс не будет в 5 наиболее вероятных) для человека: 5.1% (пруф в блоге Karpathy)
  • Top-5 ошибка для СНС: 2.0% (по крайней мере, по состоянию на конец прошлого года; сейчас, наверняка, уже ближе к проценту подбираются или даже меньше. В любом случае, можно сослаться для порядка на статью "Fixing the train-test resolution discrepancy")

А вот верификация (проверка, что пара фотографий принадлежат одному человеку) на LFW:


Можно было бы после такого сделать такой вывод:

Image credit

spectrum.ieee.org

(Не)устойчивость сверточных нейронных сетей

Но не будем спешить. Для ответа на второй вопрос обратимся к работам исследователей, которые стояли в истоках проверки СНС на устойчивость. Оказывается, можно внести практически незаметные для глаза человека возмущения во входные данные, которые, тем не менее, полностью поменяют выход нейронной сети.

Например, результат классификации с "панды" меняется на "гиббона" при внесении крайне незаметных возмущений:

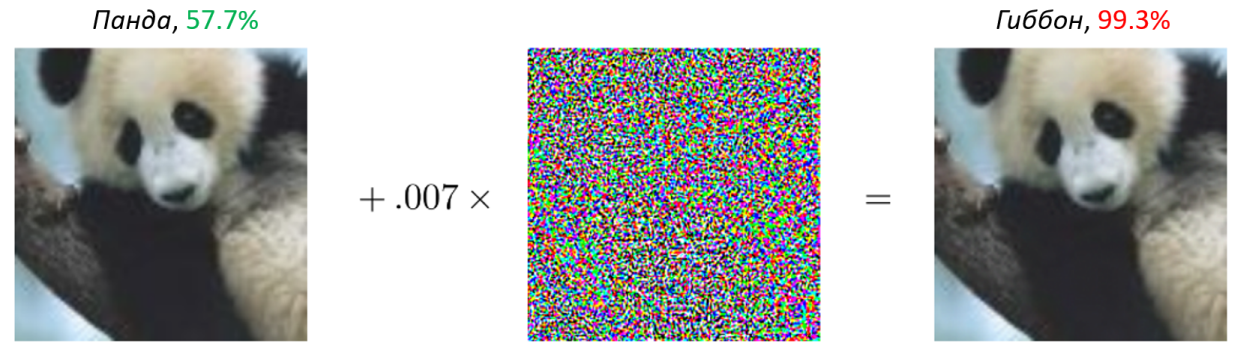
Так вот, такие почти не заметные возмущения, которые меняют выход нейросети, называют состязательными примерами (или, зачастую, атаками на эту самую нейросеть); по-английски устойчивое выражение adversarial examples / attack.

Может показаться, ну, возможно, такие состязательные примеры существуют только для классификационных сетей (ну класс там перекинуть с правильного на неправильный). Однако быстро выяснили, что подобные проблемы наблюдаются и у сетей, которые детектируют объекты (обводят прямоугольником), и даже у сегментационных сетей (которые каждому пикселю изображения сопоставлют класс): для примера можно посмотреть работу "Adversarial examples for semantic segmentation and object detection".
Ну и напоследок, предвидя возражения в виде «ну это все картинки, в нашем замечательном NLP такого не бывает!» [NLP = Natural Language Processing], можно привести замечательный пример из статьи "Adversarial examples for evaluating reading comprehension systems", который относится прежде всего к так называемым вопросно-ответным системам, в которых исследуемой системе дают небольшой кусочек текста (несколько предложений), а затем задают простой вопрос на понимание этого куска. Вот исходный текст:
Peyton Manning became the first quarterback ever to lead two different teams to multiple Super Bowls. He is also the oldest quarterback ever to play in a Super Bowl at age 39. The past record was held by John Elway, who led the Broncos to victory in Super Bowl XXXIII at age 38 and is currently Denver’s Executive Vice President of Football Operations and General Manager.
Вопрос:
What is the name of the quarterback who was 38 in Super Bowl XXXIII?

Правильный (а в данном примере он совпадает и с выходом исследуемой модели) ответ: John Elway.

Если же последним предложением к тексту добавить вот этот кусок, совершенно не относящийся к вопросу:
Quarterback Jeff Dean had jersey number 37 in Champ Bowl XXXIV.

То ответ поменяется (станет неправильным — внимание нейросети сбилось): Jeff Dean.

Откуда берется неустойчивость и способы борьбы с ней

Причин, по которым возможно такое существование состязательных примеров, не так чтобы одна (и не хочется здесь разводить холивар на эту тему — исследователи до сих не пришли к единому мнению). Остановимся на одной (и, возможно, наиболее просто интерпретируемой) — а именно, недостаточной обобщающей способности нейросетей. В силу этого границы классификации, которые строятся при обучении нейросети, зачастую проходят очень близко к обучающим данным, и порой легко «заступить» с помощью минимального возмущения из области, соотвествующей одному классу, в область, соответствующую другому классу:

Замечание на полях: по сути, техника аугментации входных данных при обучении (добавление к исходным данным их немного преобразованных вариантов: например, с помощью поворота, затемнения/засветления, масштаба и пр.) и пытается в какой-то степени решить эту проблему — отдалить границу, правда, только в некоторых направлениях (которые соответствуют выбранным аугментациям). При этом направления с очень близкими границами все равно остаются.

Итак, мы знаем, что можно обмануть СНС путем небольшого пиксельного возмущения. Почему бы во время обучения для каждого обучающего примера не добавлять и всю его попиксельную окрестность (по некоторой норме, например, $ell_{infty}$ [про нормы чуть позже]). Ниже — замечательная иллюстрация из статьи "Towards deep learning models resistant to adversarial attacks", где звездочками помечены пиксельные окрестности обучающих примеров, которые попали при изначальной разделяющей прямой в область соседнего класса — поэтому нужно разделяющую кривую преобразовать так, чтобы эти звездочки попали в область своего класса:
Ну что ж, сказано — сделано. Давайте произведем на коленке необходимые расчеты. Если предположить, что:
  • исходная картинка размера $100 imes 100$ пикселей, 3 цвета RGB,
  • наш глаз не сильно различает колебания цвета пикселей в 2 градации (из 256): в каждой точке для каждого цвета можем позволить $pm 1$ значение,

то для каждого обучающего примера нужно добавить следующее количество его пиксельных соседей:

$2^{3 imes 100 imes 100} = 2^{30000} = (2^{10})^{3000} approx (10^{3})^{3000} = 10^{9000}.$

Хочется заметить, что это значение гораздо больше числа атомов в видимой части Вселенной $(approx 10^{80})$, что разбивает на корню идею поправить дело с устойчивостью СНС простым методом «в лоб».

Как видим, простой перебор пиксельной окрестности — дело трудоемкое. Но ведь нам не нужна та окрестность обущающего примера, которая и так находится в правильной классификационной области! Нужно, наоборот, брать во внимание те точки из окрестности, которые попадают в неправильную область для классификации (по сути, эдакий hard mining обучающих примеров). И вот такой метод обучения с использованием дополнительных, наиболее сложных примеров из окрестности и называется состязательным обучением (adversarial training). В качестве матчасти можно обратиться к первоисточнику по состязательному обучению для СНС. Отметим плюсы состязательного обучения. Таким образом, уже не нужно перебирать огромные и неподъемные количества точек из окрестности, а достаточно только взять наиболее сложные. Правда, как именно брать эти «самые сложные» — вопрос хороший, и по сути, открытый до сих пор. Обычно используют некий метод генерации состязательных примеров, и таким образом получают после обучения модель, защищенную от этого метода генерации.

Минусы также достаточно очевидны. Во-первых, приобретая защиту от некого метода генерации атак, использующегося в обучении, мы не можем ничего гарантировать относительно какого-нибудь другого метода генерации состязательных примеров. А еще — любой метод генерации таких примеров добавляет приличный такой оверхед (обычно — куда больше обычного градиентного шага с использованием метода обратного распространения ошибки).

Обозначения: формальная часть

Введем парочку обозначений для более формального дальнейшего изложения:

  • Пусть $xin B=[0,1]^{C imes M imes N}$ — входная картинка $C imes M imes N$, где $C$ — количество цветов (1 для черно-белой, 3 для цветной в формате RGB), $M imes N$ — пространственные размерности (ширина, высота);
  • $y_{gt}$ — правильный класс для входа $x$;
  • $ heta$ — параметры СНС-классификатора;
  • $L( heta, x, y_{gt})$ — функция потерь;
  • $f(x)$ — выход классификатора (распознанный класс); при обучении мы добиваемся равенства $f(x) = y_{gt}$;
  • $rin B=[0,1]^{C imes M imes N}$ — аддитивная добавка ко входу $x$;

Теперь можно формально определить цель состязательной атаки: поменять выход классификатора $f$ на неправильный путем добавления минимального по некоторой норме (на практике используются $ell_{0}, ell_{1}, ell_{2}mbox{ и }ell_{infty}$ — обозначим через $ell_{p}$) возмущения $r$, а именно минимизировать $||r||_{p}$ так, чтобы:

  1. $f(x) = y_{gt}$ (изначально правильно определяем класс),
  2. $f(x+r) eq y_{gt}$ («ломаем» СНС с помощью возмущения r),
  3. $x+rin B$ (остаемся во множестве допустимых значений).

Замечание на полях. Похожим образом можно определить и такое понятие, как устойчивость классификатора — найти такой класс возмущения $S(x,f)subseteq B$, при котором классификатор не меняет свой выход: $f(x+r) = f(x)quad forall rin S(x, f)$.

В обозначениях выше обычное обучение СНС на примерах можно сформулировать как минимизацию следующего матожидания:

$min_{ heta}mathbb{E}_{(x,y_{gt})}[L( heta, x, y_{gt})]$

В состязательном обучении мы сначала генерируем (например, каким-нибудь методом атаки) самый сложный пример из некоторой окрестности $Delta$ входного примера (например, по $ell_{p}$-норме), а уже затем минимизируем по параметрам нейросети:

$min_{ heta}mathbb{E}_{(x,y_{gt})}[max_{rinDelta}L( heta, x+r, y_{gt})]$

Нормы l_p: напоминание
Напомним наиболее употребительные нормы $ell_{p}$ для $x = (x_{1}, dots, x_{n})inmathbb{R}^{n}$:

  • $ell_{2}$: $||x||_{2} = sqrt{sum_{i=1}^{n}x_{i}^{2}}$ (обычная Евклидова норма);
  • $ell_{1}$: $||x||_{1} = sum_{i=1}^{n}|x_{i}|$ (т.н. метрика городских кварталов);
  • $ell_{infty}$: $||x||_{infty} = max_{i}|x_{i}|$ (максимум модуля; именно на основе данной метрики человеческий глаз воспринимает зрительную информацию);
  • $ell_{0}$: $||x||_{0} = sum_{i=1}^{n}mathbf{1}_{x_{i} eq 0}$ (число ненулевых значений).

Замечание. Для $0 < p < 1$ «норма» $ell_{p}$, для которой $||x||_{p} = left(sum_{i=1}^{n}|x_{i}|^{p} ight)^{1/p}$, не является нормой.

Состязательные примеры в компьютерном зрении: история вопроса

Fooling images

Допустим, у нас есть классификатор, который выдает вероятности принадлежности входной картинки к 1 из N предобученных классов (например, N=1000 в случае с ImageNet). И, допустим (это не всегда так, но все же), на картинках, принадлежащих этим классам, вероятности выдаются более-менее осмысленно (хоть и бывают ошибки, конечно). Но что будет, если подадим на вход картинку, не принадлежащую этим N классам — то есть, выражаясь математически, вне области определения? И хорошо, если на выходе будет равномерный вектор вида (1/N, ..., 1/N) — типа сеть не понимает, что происходит.

Гораздо хуже, когда на объекте вне области определения сеть выдает некий очень определенный ответ — то есть одна из вероятностей будет сильно больше других. Так вот, изначально устойчивость СНС изучалась с точки зрения адекватной реакции на разные входы. Выяснилось, что существуют примеры (построенные на основе некой структуры, либо являющиеся по сути белым шумом), которые на выходе СНС могут давать с большой вероятностью любой (в том числе и заранее определенный) класс.

Такие примеры назывались "обманными изображениями" (fooling images) и строились с помощью эволюционных алгоритмов:

За деталями любопытный читатель может обратиться к первоисточнику "Deep neural networks are easily fooled: High confidence predictions for unrecognizable images".

FGSM

В самом первом методе атаки СНС использовался квази-Ньютоновский метод минимизации с ограничением на память и на переменные L-BFGS-B — но этот метод достаточно медленный, да и требует зачастую внешнего оптимизатора. Поэтому практически сразу было предложено использовать линейную часть функции потерь в окрестности входной картинки $x$ и идти по градиенту (см. первоисточник "Explaining and harnessing adversarial examples"):

$r = epsiloncdot sign( abla_{x}L( heta, x, y_{t}))$

где $0 < epsilon < 1$ — некоторая константа, отвечающая за скорость движения, а $y_{t} eq y_{gt}$ — неправильный класс, в направлении которого мы «подталкиваем» (обманываем) смотреть СНС.

Такой метод получил название Fast Gradient Sign Method (по-русски "быстрый метод, основанный на знаке градиента", но звучит все равно не очень), или FGSM.

Напоминание: для оптимизации весов СНС применяется метод обратного распространения ошибок, где берется градиент по весам СНС, т.е. $ abla_{ heta}L( heta, x, y_{gt})$.

Ну и в данной работе исследуется норма возмущения $ell_{infty}$ как наиболее близкая к тому, как устроено человеческое зрение (восприятие зрительной информации).

I-FGSM (PGD)

Часто линейная оценка окрестности функции достаточно грубая, и один шаг FGSM порой не приводит к хорошей атаке.

Для преодоления данной проблемы применяют итеративный метод Iterative FGSM, или I-FGSM, который позволяет двигаться в сторону границы классификатора более точно. Если $Pi_{B}$ — проекция на $B$, то

$x^{n+1} = Pi_{B}(x^{n} + alphacdot sign( abla_{x}L( heta, x, y_{gt}))), quad x^{0}=x$

При этом если мы хотим, чтобы наше итоговое решение $x_{adv}$ «отдалилось» от исходного примера $x$ не более чем на $epsilon$ по норме $ell_{infty}$, и мы можем сделать не более $n$ шагов, то можно сразу вывести эмпирическое правило на скорость движения:

$alpha = frac{epsilon}{n}$

Замечание 1. Но в целом метод I-FGSM гораздо более известен как метод спроектированного градиентного спуска Projected Gradient Descent, или PGD, хотя и появилось это название чуть ли не на год позже. Замечание 2. Вообще, метод I-FGSM / PGD до сих пор является наиболее широкоприменяемым на практике как простой и при этом достаточно устойчивый (хотя и не такой быстрый, как простой FGSM).

MI-FGSM

Как внимательный читатель мог заметить, методы генерации состязательных примеров все больше и больше похожи на шаги оптимизатора, который используется при нахождении оптимальных весов СНС (только в случае обучения СНС мы оптимизируем по весам, а в случае с состязательными примерами — по входу).

Поэтому в целом возникает целый тренд перетягивания успешных подкруток градиентного спуска в состязательную область, и самый успешный такой пример — использование момента. Как следствие, работа "Boosting adversarial attacks with momentum" предлагает использовать сглаживание градиента в итеративном методе I-FGSM — Momentum I-FGSM, или MI-FGSM.

Схема работы следующая:

$x^{n+1} = Pi_{B}(x^{n} + alphacdot sign(g^{t+1})), quad x^{0}=x, g^{0} = 0$

где через g обозначен как раз сглаженный градиент:

$g^{n+1} = mucdot g^{n} + frac{ abla_{x}L( heta, x, y_{gt})}{|| abla_{x}L( heta, x, y_{gt})||_{1}}$

Ну и табличка сравнения последних трех методов, из которой видно, что MI-FGSM все-таки предпочтительнее использовать (чем больше циферки, тем выше успешность атаки):

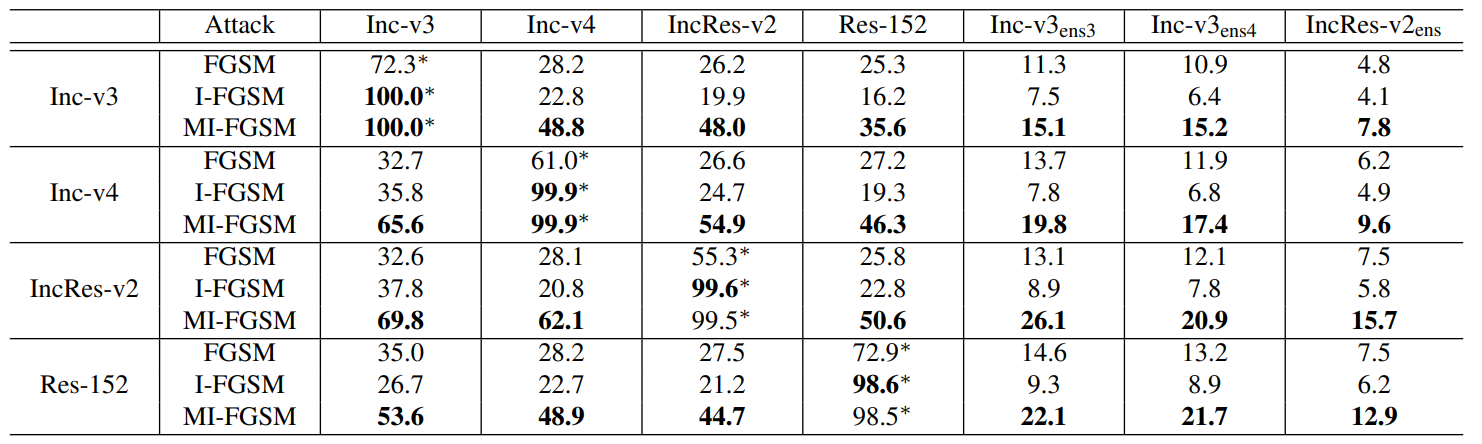
One Pixel

До этого мы рассматривали состязательные атаки в цифровой области, когда можно менять вообще любой пиксель входного изображения. Тем не менее, есть методы (один из первых — JSMA, но он не очень практичный и удобный), которые принимают во внимание не максимальную разность по яркости (по норме $ell_{infty}$), а максимальное количество пикселей, который можно поменять (по норме $ell_{0}$).

Такие методы состязательных примеров являются мостиком между цифровой и практической областью (материал о практических состязательных примерах см. в следующей части), и наиболее экстремальной является однопиксельная атака.

В работе "One pixel attack for fooling deep neural networks" рассматривается предельный случай $ell_{0}$-атаки. Для этого авторы применяют эволюционный алгоритм (а именно, алгоритм дифференциальной эволюции) для поиска состязательных примеров:

  • Популяция состоит из 400 экземпляров, каждый из которых задается пятеркой чисел: две координаты и три канала цвета;
  • Генерация потомка — линейная комбинация трех случайных родителей.

Ниже — пример такой атаки на базе CIFAR-10, где исходная картинка собаки при изменении ровно одного пикселя становится поочередно любым из остальных 9 классов (самолет, ..., грузовик):

Краткие выводы по первой части

  • На данный момент СНС (в целом) работают гораздо лучше человека;
  • СНС легко «обмануть», используя их неустойчивость по входу;
  • Наиболее распространенный ингредиент для генерации состязательного примера — градиент нейросети по входу.

Ссылки

  • Введение «на пальцах» в тему состязательных атак, прочитанное в 2019 году на Фестивале науки в МГУ им. М. В. Ломоносова:

  • Чуть больше математики — заключительная лекция курса "Современное компьютерное зрение", читаемого в рамках программы SHARE в МГУ им. М. В. Ломоносова для студентов и аспирантов факультетов механико-математического, физического, космических исследований и ВМиК.

Бонус: программа SHARE

В 2019 году в Huawei стартовала образовательная программа SHARE: Школа опережающего научного образования Хуавэй (School of Huawei Advanced Research Education).

Наша лаборатория — Intelligent Systems and Data Science Technology Center — проводит занятия в МГУ им. М. В. Ломоносова.

Основные факты по данной программе:

  • 2 года длится обучение;
  • 12 полносеместровых курсов в составе (планируем расширять — нужно больше практических занятий, это то, чего просят студенты в своих отзывах на наши курсы);
  • 2 главных направления в составе (на данный момент ведем переговоры о включении третьего про обучение с подкреплением):
  • Специализация "Компьютерное зрение и машинное обучение'';
  • Специализация "Большие данные и теория информации''.

В будущем будем наполнять содержимое сайта программы (пока только домен зарегистрировали, но работа идет полным ходом ;)

Трейлер следующей части

В следующий раз разберем:

  • Что такое физически реализуемая состязательная атака;
  • Основные методы генерации физических состязательных примеров;
  • Сбиваем с толку реальный детектор лиц;
  • Делаем больно лучшему открытому распознавателю лиц;
  • Рассматриваем методику защиты от физических состязательных атак.

Спасибо за внимание!


Источник: habr.com

Комментарии: