Игровые древа и матрицы в Теории игр ?

Игровые древа

Различие между играми с идеальной и несовершенной информацией связано (хотя, конечно, не идентично!) посредством различий между способами представления игры, основанными на её порядке.

Давайте начнём с рассмотрения различий между играми с поочерёдными ходами и играми с одновременно доступным ходом (с точки зрения наличия информации).

При первом углублении в эту тему, естественно подумать об играх с поочерёдным ходом как об играх, в которых игроки выбирают свои стратегии одну за другой, а об играх с одновременным ходом - как об играх, в которых игроки выбирают свои стратегии одновременно. Однако подобное представление не совсем правильно, потому-что стратегическое значение имеет не временной порядок событий как таковой, а то, знают ли игроки о контр-действиях соперников относительно их собственных действий, и когда именно эти контр-выпады могут произойти.

Например, если два конкурирующих предприятия планируют маркетинговые кампании, одно может начать реализацию своей стратегии за несколько месяцев до того, как это сделает другое; но если в тот момент, когда они принимают свои решения, ни одно из них не знает, что именно конкуренты обязались или планируют делать, тогда это будет игра с одновременными ходами.

В шахматы же, напротив, обычно играют с поочерёдными ходами: Вы видите, что сделал Ваш противник, прежде чем выбрать свой следующий ход (правда, шахматы можно превратить и в игру с одновременными ходами, если оба игрока движутся по общей доске, будучи изолированными друг от друга; но это уже будет совсем другая игра, а не обычные шахматы).

Выше было сказано, что различие между играми с последовательным ходом и играми с одновременным ходом не идентично различию между играми с идеальной и несовершенной информацией. Объяснение того, почему это так, - хороший способ полностью понять оба набора концепций. Поскольку игры с одновременным ходом были охарактеризованы в предыдущем абзаце, логично прийти к выводу, что все игры с одновременным ходом являются играми с несовершенной информацией. Однако некоторые игры могут содержать сочетание последовательных и одновременных ходов. Например, две фирмы могут придерживаться своих маркетинговых стратегий независимо и в секрете друг от друга, но дальше вступают в ценовую конкуренцию на виду друг у друга. Если бы оптимальные маркетинговые стратегии частично или полностью зависели от того, что ожидалось в последующей игре с ценообразованием, то эти два этапа нужно было бы анализировать как одну игру, в которой этап последовательной игры следует за этапом одновременной игры. Многие игры, включающие в себя смешанные стадии подобного рода, представляют собой игры с несовершенной информацией, каким бы таймфреймом они ни обладали. Игры с идеальной информацией (как следует из названия) обозначают случаи, когда никакие ходы не являются одновременными (и где ни один игрок никогда не забывает, что было сделано ранее).

Как известно, игры с идеальной информацией - это (логически) простейшие виды игр. Так происходит потому, что в таких играх (пока они конечны, то есть завершаются после известного количества действий) игроки и аналитики могут использовать простую процедуру для прогнозирования результатов. Игрок в такой игре выбирает своё новое действие, рассматривая каждую серию ходов и встречных ходов, которые будут результатом каждого действия, доступного для реализации. Затем он спрашивает себя, какой из доступных конечных результатов принесёт ему наибольшую пользу, и выбирает действие, которое запускает цепочку, ведущую к этому результату. Этот процесс называется обратной индукцией (поскольку рассуждения работают в обратном направлении: от конечных результатов - к решению проблем выбора).

Об обратной индукции и её свойствах будет сказано гораздо больше в следующих публикациях (когда мы перейдем к обсуждению равновесия и равновесного выбора). На данный момент этот аспект был вкратце упомянут только для того, чтобы мы могли использовать его для рассмотрения одного из двух типов математических методов, используемых для представления игр: игровых древ.

Древо игры - это пример того, что математики называют орграфом (или ориентированным графом). То есть это набор связанных узлов, в которых общий граф имеет вектор. Мы можем рисовать древа сверху-вниз или слева-направо. В первом случае узлы вверху страницы интерпретируются как приходящие раньше в последовательности действий. В случае древа, нарисованного слева направо, левые узлы имеют приоритет в последовательности перед правыми. Дерево без метки имеет следующую структуру:

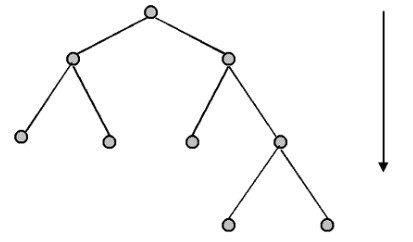
Суть представления игр с использованием древ может быть лучше всего понята путём визуализации их использования в поддержку цепочки рассуждений обратной индукции. Только представьте, что игрок (или аналитик) начинает с конца древа, где отображаются результаты, а затем работает в обратном направлении от них, ища наборы стратегий, которые описывают пути, ведущие к этим результатам. Поскольку функция полезности игрока указывает, какие результаты он предпочитает, мы также можем предугадать, какие пути он выберет. Конечно, не все пути будут возможны, потому-что другой игрок тоже вносит влияние на выбор тактики, и не будет предпринимать действий, которые откроют пути к менее предпочтительным для него результатам. Мы представим несколько примеров этого интерактивного выбора пути и подробные методы рассуждений с помощью этих примеров, после того как опишем ситуацию, которую можно использовать для моделирования древа.

Игровые матрицы

Древа используются для представления последовательных игр, поскольку они показывают порядок действий, выполняемых игроками. Однако иногда игры представляют не древами, а матрицами. Это второй тип математических методов, используемых для представления игр. Матрицы, в отличие от древ, просто показывают результаты, представленные в терминах функций полезности игроков, для каждой возможной комбинации стратегий, которые игроки могут использовать. Например, имеет смысл отобразить игру о переправе через реку из статьи 1 на матрице, поскольку в этой игре и у беглеца, и у охотника есть только один ход, и каждый выбирает свой ход, не зная, что решил сделать другой. Итак, вот часть этой матрицы (где Hunter - охотник, а Fugitive - беглец):

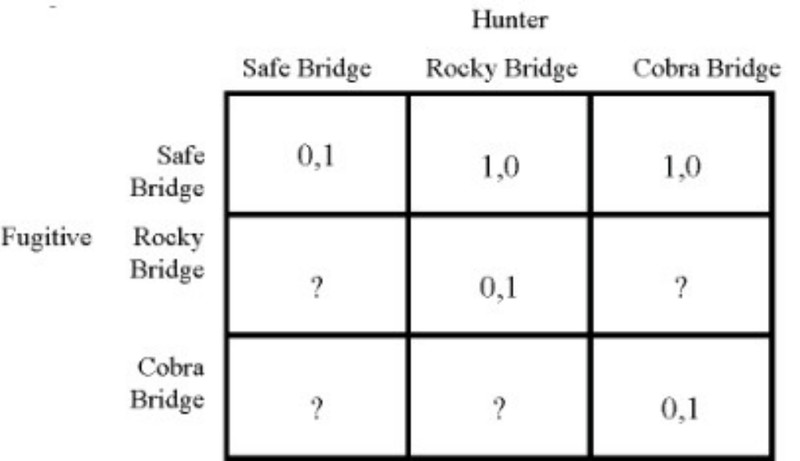
Три возможных стратегии беглеца - перейти через безопасный мост (Safe Bridge), рискнуть пройти по мосту с камнепадами (Rocky Bridge) или рискнуть пересечь мост с кобрами (Cobra Bridge) - образуют горизонтальные ряды матрицы. Точно так же три возможные стратегии охотника - ожидание у безопасного моста, ожидание у каменистого моста и ожидание у моста с кобрами - образуют вертикальные столбцы матрицы. Каждая ячейка матрицы показывает - или, скорее, показывала бы, была ли наша матрица полной - результат, определенный в терминах выигрышей игроков. Выигрыш игрока - это просто число, присвоенное его функцией полезности при положении дел, соответствующем рассматриваемому исходу. Для каждого результата выигрыш по строке всегда указывается первым, а за ним идёт столбец. Таким образом, например, верхний левый угол выше показывает, что, когда беглец переходит через безопасный мост и охотник тоже ждёт там, беглец получает выигрыш 0, а охотник получает выигрыш 1. Мы интерпретируем это при отсылке к функциям полезности двух игроков, которые в этой игре очень просты. Если беглец благополучно переправляется через реку, он получает выигрыш 1; если он этого не делает, он получает 0. Если беглец не пересекает мост потому, что он застрелен охотником (а не ранен камнем, либо укушен коброй), тогда охотник получает выигрыш 1, а беглец совсем не получает выплаты.

Кратко объясним, какие части матрицы были заполнены, а затем скажем, почему пока нельзя заполнить остальные.
Каждый раз, когда охотник ждёт у моста, выбранного беглецом, беглец оказывается застреленным. Все эти исходы предоставляют векторы выигрыша в размере 0,1. Вы можете найти их, спускаясь по диагонали через матрицу из верхнего левого угла - в нижний правый. Каждый раз, когда беглец выбирает безопасный мост, а охотник ждет у другого, беглец благополучно переходит его, получая выигрыш = 1. Эти два результата показаны во вторых двух ячейках верхнего ряда. Все остальные ячейки пока отмечены вопросительными знаками. Почему? Проблема здесь в том, что если беглец пересекает скалистый мост или мост кобр, он вводит в игру параметрические факторы. В этих случаях он берёт на себя некоторый риск быть убитым не пулей, а камнями или ядовитой змеёй, и, таким образом, создает вектор выигрыша 0.1, который не зависит от того, что делает охотник. У нас ещё недостаточно представленных концепций, чтобы показать, как рассчитать эти результаты в терминах функций полезности, но к тому времени, когда мы закончим цикл публикаций, читатель уже будет оперировать большим числом концепций, и это даст ключи к решению нашей головоломки из статьи 1.

И последнее на сегодня...

Игры стратегической и расширенной формы

Матричные игры называются играми "нормальной формы" или "стратегической формы", а игры с основой в виде древ называются играми "расширенной формы". Эти два типа игр не эквивалентны, потому-что игры с расширенной формой содержат информацию о последовательностях игры и уровнях информации игроков об игровой структуре, - чего нет в играх стратегической формы.
В общем, игра в стратегической форме может представлять любую из нескольких игр расширенной формы, поэтому игру в стратегической форме лучше всего рассматривать как симбиоз нескольких игр расширенной формы.

Когда порядок игры не имеет отношения к исходу игры, Вам следует изучить её стратегическую форму, поскольку это даст охват всего набора параметров, о которых важно знать. Если же порядок игры имеет значения, необходимо предпочесть развёрнутую форму анализа, иначе Ваши выводы будут недостоверными.