Учебный проект на Python: алгоритм Дейкстры, OpenCV и UI ( часть 1)

Лабиринты — это распространенная головоломка для людей, но они представляют из себя интересную задачу для программирования, которую мы можем решить, используя методы кратчайшего пути, такие как алгоритм Дейкстры.

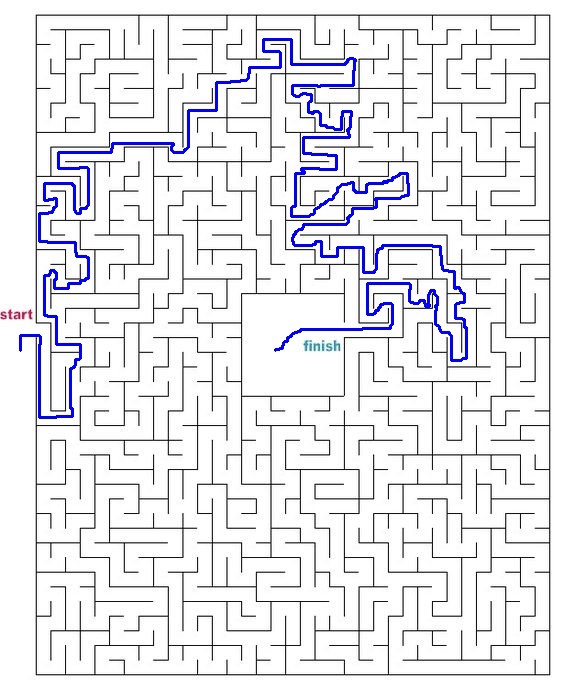
Вспоминаем алгоритм Дейкстры

Алгоритм Дейкстры — один из наиболее популярных алгоритмов теории графов. Он используется для поиска кратчайшего пути между узлами на ориентированном графе. Мы начнем с исходного узла и известных длин ребер между узлами.

Сначала мы присваиваем значение расстояния от источника всем узлам. Узел s получает значение 0, потому что это источник; остальные получают значения ? для начала.

Наш интересующий узел — это необработанный узел с наименьшим значением (показан серым), то есть s. Сначала мы «ослабляем» каждую смежную вершину до нашего интересующего узла, обновляя их значения до минимума их текущего значения или значения узла интереса плюс длину соединительного ребра…

Узел s теперь завершен (черный), а его соседи a и b приняли новые значения. Новый интересующий узел — b, поэтому мы повторяем процесс «ослабления» соседних узлов b и финализации значения кратчайшего пути для b.

Пройдя через каждый узел, мы в итоге получим график, показывающий кратчайшую длину пути от источника до каждого узла.

Наша финальная диаграмма после запуска алгоритма Дейкстры. Числа в каждом узле представляют кратчайшее возможное расстояние от исходного узла.

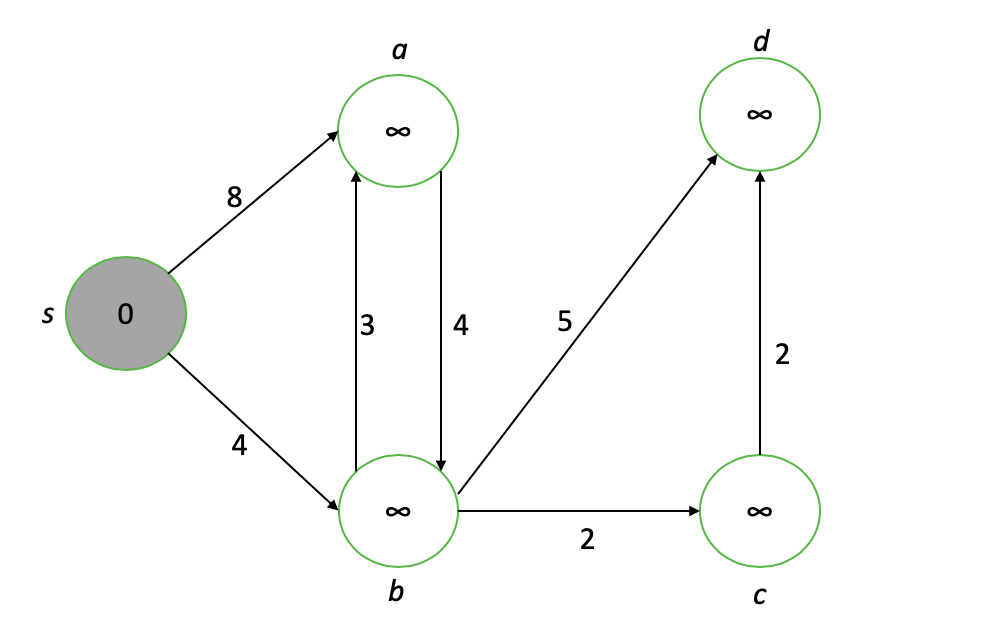
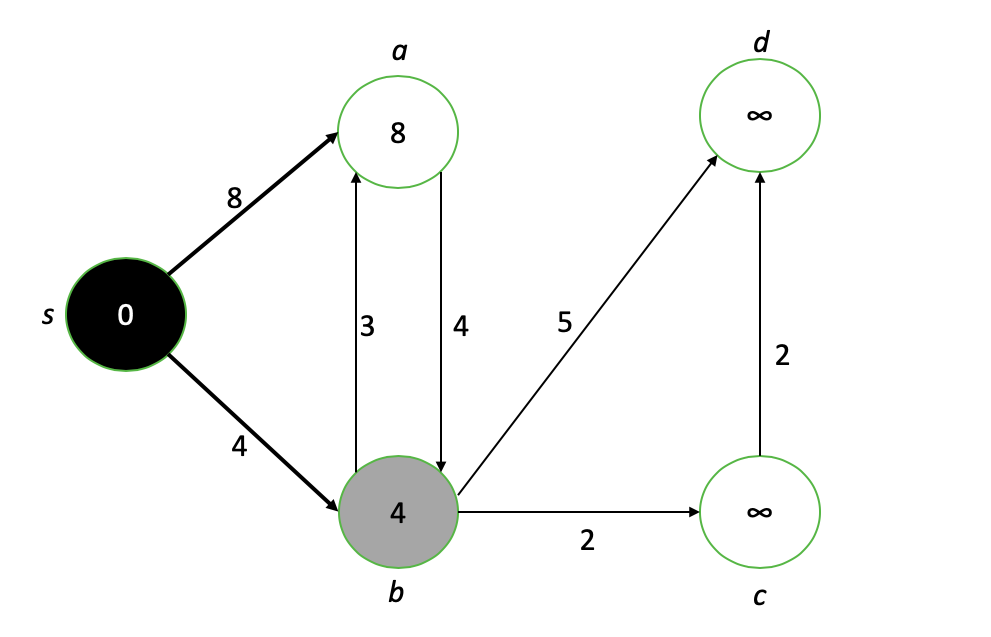
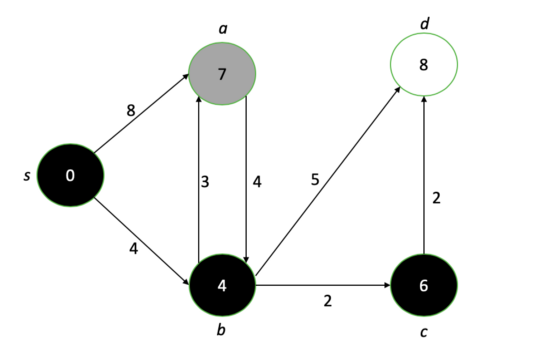
Концептуализация изображений лабиринта

Мы можем представить себе изображение как матрицу пикселей. Каждый пиксель (для простоты) имеет значение RGB 0,0,0 (черный) или 255,255,255 (белый). Наша цель — создать кратчайший путь, который начинается на белом и не переходит на чёрные границы. Чтобы представить эту цель, мы можем рассматривать каждый пиксель как узел и рисовать ребра между соседними пикселями с длиной ребер, основанной на разнице значений RGB. Мы будем использовать формулу евклидова квадратного расстояния и добавим 0,1, чтобы гарантировать отсутствие длины пути 0 — (требование для алгоритма Дейкстры):

Эта формула делает расстояние пересечения через границу лабиринта чрезмерно большим. Как мы видим, кратчайший путь от источника к месту назначения будет четко проходить вокруг барьера, а не через него.

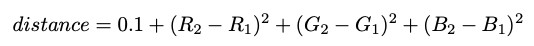
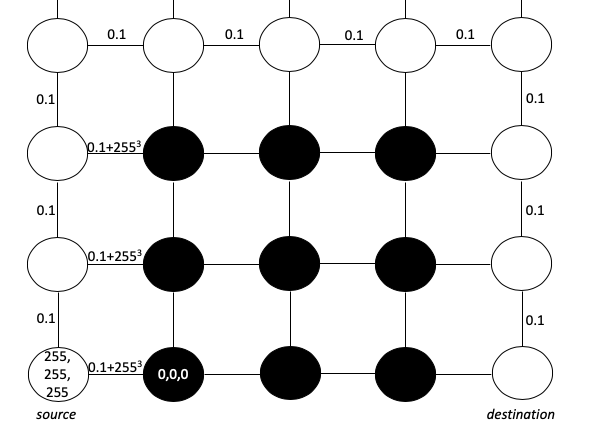
Реализация

Мы можем использовать OpenCV, популярную библиотеку компьютерного зрения для Python, чтобы извлечь значения пикселей и показать наши изображения лабиринта. Давайте также определим координаты нашего начального и конечного местоположений, добавив точки в наш лабиринт

import cv2 import matplotlib.pyplot as plt import numpy as np img = cv2.imread('maze.png') # read an image from a file using cv2.circle(img,(5,220), 3, (255,0,0), -1) # add a circle at (5, 220) cv2.circle(img, (25,5), 3, (0,0,255), -1) # add a circle at (5,5) plt.figure(figsize=(7,7)) plt.imshow(img) # show the image plt.show()

Мы создаем класс Vertex, который поможет нам отслеживать координаты. Мы также хотим отслеживать родительский узел, чтобы мы могли восстановить весь путь, как только найдем значения расстояния.

class Vertex:     def __init__(self,x_coord,y_coord):         self.x=x_coord         self.y=y_coord         self.d=float('inf') #current distance from source node         self.parent_x=None         self.parent_y=None         self.processed=False         self.index_in_queue=None

Нам нужно создать матрицу вершин, представляющую двухмерное расположение пикселей на изображении. Это будет основой для алгоритма Дейкстры. Мы также поддерживаем очередь с минимальной кучей приоритетов для отслеживания необработанных узлов.

def find_shortest_path(img,src,dst):     pq=[] #min-heap priority queue     imagerows,imagecols=img.shape[0],img.shape[1]     matrix = np.full((imagerows, imagecols), None)      #access matrix elements by matrix[row][col]     #fill matrix with vertices     for r in range(imagerows):         for c in range(imagecols):             matrix[r][c]=Vertex(c,r)             matrix[r][c].index_in_queue=len(pq)             pq.append(matrix[r][c])     #set source distance value to 0     matrix[source_y][source_x].d=0     #maintain min-heap invariant (minimum d Vertex at list index 0)     pq = bubble_up(pq, matrix[source_y][source_x].index_in_queue)

Нам нужно несколько вспомогательных функций, чтобы помочь найти ребра и длину ребер между вершинами:

#Implement euclidean squared distance formula def get_distance(img,u,v):     return 0.1 + (float(img[v][0])-float(img[u][0]))**2+(float(img[v][1])-float(img[u][1]))**2+(float(img[v][2])-float(img[u][2]))**2 #Return neighbor directly above, below, right, and left def get_neighbors(mat,r,c):     shape=mat.shape     neighbors=[]     #ensure neighbors are within image boundaries     if r > 0 and not mat[r-1][c].processed:          neighbors.append(mat[r-1][c])     if r < shape[0] - 1 and not mat[r+1][c].processed:             neighbors.append(mat[r+1][c])     if c > 0 and not mat[r][c-1].processed:         neighbors.append(mat[r][c-1])     if c < shape[1] - 1 and not mat[r][c+1].processed:             neighbors.append(mat[r][c+1])     return neighbors

Теперь мы можем реализовать алгоритм Дейкстры и присвоить значения расстояния (d) всем вершинам пикселей в изображении лабиринта:

while len(pq) > 0:     u=pq[0] #smallest-value unprocessed node     #remove node of interest from the queue     pq[0]=pq[-1]      pq[0].index_in_queue=0     pq.pop()     pq=bubble_down(pq,0) #min-heap function, see source code           u.processed=True     neighbors = get_neighbors(matrix,u.y,u.x)     for v in neighbors:         dist=get_distance(img,(u.y,u.x),(v.y,v.x))         if u.d + dist < v.d:             v.d = u.d+dist             v.parent_x=u.x #keep track of the shortest path             v.parent_y=u.y             idx=v.index_in_queue             pq=bubble_down(pq,idx)              pq=bubble_up(pq,idx)

Теперь мы можем вызвать функцию кратчайшего пути и нарисовать решение в нашем лабиринте:

img = cv2.imread('maze.png') # read an image from a file using opencv (cv2) library p = find_shortest_path(img, (25,5), (5,220)) drawPath(img,p) plt.figure(figsize=(7,7)) plt.imshow(img) # show the image on the screen  plt.show()

Давайте попробуем другие лабиринты со всего Интернета.

Полный исходный код доступен на GitHub здесь.