Книга «Обработка естественного языка в действии»

Мы издали практическое руководство по обработке и генерации текстов на естественном языке. Книга снабжена всеми инструментами и методиками, необходимыми для создания прикладных NLP-систем с целью обеспечения работы виртуального помощника (чат-бота), спам-фильтра, программы — модератора форума, анализатора тональностей, программы построения баз знаний, интеллектуального анализатора текста на естественном языке или практически любого другого NLP-приложения, какое только можно себе представить.
Книга ориентирована на Python-разработчиков среднего и высокого уровня. Значительная часть книги будет полезна и тем читателям, которые уже умеют проектировать и разрабатывать сложные системы, поскольку в ней содержатся многочисленные примеры рекомендуемых решений и раскрываются возможности самых современных алгоритмов NLP. Хотя знание объектно-ориентированного программирования на Python может помочь создавать лучшие системы, для использования приводимой в этой книге информации оно не обязательно.

Нейронные сети с обратной связью: рекуррентные нейронные сети

В главе 7 продемонстрированы возможности анализа фрагмента или целого предложения с помощью сверточной нейронной сети, отслеживание соседних слов в предложении путем наложения на них фильтра разделяемых весов (выполнения свертки). Встречающиеся группами слова можно также обнаруживать в связке. Сеть также устойчива к небольшим смещениям позиций этих слов. В то же время встречающиеся по соседству понятия могут существенно влиять на сеть. Но если нужно охватить взглядом большую картину происходящего, учесть взаимосвязи за более длительный промежуток времени, окно, охватывающее больше 3–4 токенов из предложения? Как ввести в сеть понятие произошедших ранее событий? Память?

Для каждого тренировочного примера (или батча неупорядоченных примеров) и выходного сигнала (или пакета выходных сигналов) нейронной сети прямого распространения веса нейронной сети необходимо откорректировать для отдельных нейронов на основе метода обратного распространения ошибки. Это мы уже демонстрировали. Но результаты этапа обучения для следующего примера в основном не зависят от порядка входных данных. Сверточные нейронные сети стремятся захватить эти отношения порядка за счет захвата локальных взаимосвязей, но существует и другой способ.

В сверточной нейронной сети каждый тренировочный пример передается сети в виде сгруппированного набора токенов слов. Векторы слов сгруппированы в матрицу в форме (длина вектора слова ? число слов в примере), как показано на рис. 8.1.

Но эту последовательность векторов слов можно столь же легко передать и обычной нейронной сети прямого распространения из главы 5 (рис. 8.2), правда? Безусловно, это вполне работоспособная модель. При подобном способе передачи входных данных нейронная сеть прямого распространения сможет реагировать на совместные вхождения токенов, что нам и нужно. Но она будет при этом реагировать на все совместные вхождения одинаково, независимо от того, разделяет ли их длинный текст, или они находятся рядом друг с другом. Кроме того, нейронные сети прямого распространения, как и CNN, плохо умеют обрабатывать документы переменной длины. Они не способны обработать текст в конце документа, если он выходит за пределы ширины сети. Лучше всего нейронные сети прямого распространения проявляют себя в моделировании взаимосвязи выборки данных в целом с соответствующей ей меткой. Слова в начале и в конце предложения ровно так же влияют на выходной сигнал, как и посередине, невзирая на то что вряд ли они семантически связаны друг с другом. Подобная однородность (равномерность влияния) явно может вызывать проблемы в случае, например, токенов резкого отрицания и модификаторов (прилагательных и наречий), таких как «нет» или «хороший». В нейронной сети прямого распространения выражающие отрицание слова влияют на смысл всех слов в предложении, даже сильно удаленных от места, на которое они должны влиять на самом деле. Одномерные свертки — способ решения проблем с этими взаимосвязями между токенами путем анализа нескольких слов через окна. Обсуждавшиеся в главе 7 слои субдискретизации специально предназначены для учета небольших изменений порядка слов. В этой главе мы рассмотрим другой подход, благодаря которому сможем сделать первый шаг к понятию памяти нейронной сети. Вместо того чтобы разбирать язык как большую порцию данных, мы начнем рассматривать его последовательное формирование, токен за токеном, с ходом времени.

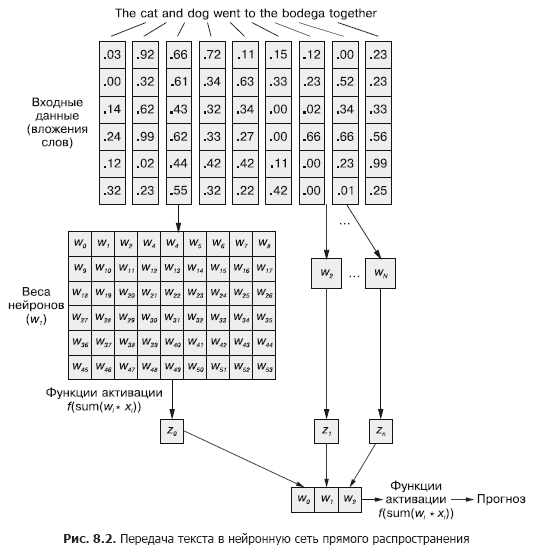
8.1. Запоминание в нейронных сетях

Конечно, слова в предложении редко бывают совершенно независимыми друг от друга; их вхождения влияют или подвергаются влиянию вхождений других слов в документе. Например: The stolen car sped into the arena и The clown car sped into the arena.

У вас могут возникнуть совершенно различные впечатления от этих двух предложений, когда вы дочитаете до конца. Конструкция фразы в них одинакова: прилагательное, существительное, глагол и предложный оборот. Но замена прилагательного в них радикальным образом меняет суть происходящего с точки зрения читателя.

Как смоделировать подобную взаимосвязь? Как понять, что arena и даже sped могут иметь немного разные коннотации, если перед ними в предложении есть прилагательное, не являющееся прямым определением ни одного из них?

Если бы существовал способ запоминать произошедшее моментом ранее (особенно помнить на шаге t + 1 произошедшее на шаге t), можно было бы выявлять закономерности, возникающие при появлении определенных токенов в связанных с другими токенами последовательности закономерностях. Рекуррентные нейронные сети (RNN) как раз делают возможным запоминание нейронной сетью прошлых слов последовательности.

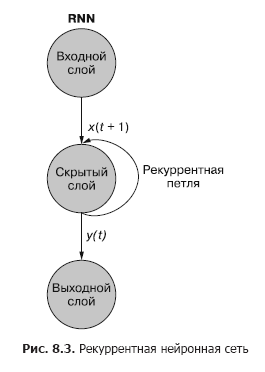
Как вы видите на рис. 8.3, отдельный рекуррентный нейрон из скрытого слоя добавляет в сеть рекуррентный цикл для «повторного использования» выходного сигнала скрытого слоя для момента t. Выходной сигнал для момента t прибавляется к следующему входному сигналу для момента t + 1. В результате обработки сетью этого нового входного сигнала на временном шаге t + 1 получается выходной сигнал скрытого слоя для момента t + 1. Этот выходной сигнал для момента времени t + 1 далее повторно используется сетью и включается во входной сигнал на временном шаге t + 2 и т. д.

Хотя идея воздействия на состояние сквозь время выглядит немного запутанной, основная концепция проста. Результаты каждого сигнала на входе обычной нейронной сети прямого распространения на временном шаге t используются в качестве дополнительного входного сигнала вместе со следующим фрагментом подаваемых на вход сети данных на временном шаге t + 1. Сеть получает информацию не только о происходящем сейчас, но и о происходившем ранее.

В этой и следующей главах большая часть нашего обсуждения происходит на языке временных шагов. Это вовсе не то же самое, что отдельные примеры данных. Речь идет о разбиении одного примера данных на меньшие порции, отражающие изменения во времени. Этот отдельный пример данных все равно представляет собой фрагмент текста, скажем короткий отзыв о фильме или твит. Как и ранее, мы токенизируем предложение. Но вместо того, чтобы отправлять токены в сеть все сразу, мы передаем их по одному. Эта схема отличается от передачи нескольких новых примеров документов. Токены при этом остаются частью одного примера данных, которому соответствует одна метка.

t можно считать индексом последовательности токенов. Так, t = 0 — первый токен в документе, а t + 1 — следующий. Токены в порядке следования их в документе служат входными сигналами на каждом из временных (токенных) шагов. Причем токены не обязательно должны быть словами, отдельные символы также допустимы. Подача примера данных в сеть разбивается на подшаги — ввод в сеть отдельных токенов.

На протяжении всей этой книги мы будем обозначать текущий временной шаг t, а следующий временной шаг — t + 1.

Рекуррентную нейронную сеть можно визуализировать так, как показано на рис. 8.3: круги соответствуют целым слоям нейронной сети прямого распространения, состоящим из одного или нескольких нейронов. Выходной сигнал скрытого слоя выдается сетью как обычно, но затем поступает обратно в качестве своего же (скрытого слоя) входного сигнала вместе с обычными входными данными следующего временного шага. На схеме этот цикл обратной связи изображен в виде дуги, ведущей из выхода слоя обратно на вход.

Более простой (и чаще используемый) способ иллюстрации этого процесса — с использованием развертывания сети. Рисунок 8.4 демонстрирует сеть «вверх ногами» с двумя развертками временной переменной (t) — слоями для шагов t + 1 и t + 2.

Каждому из временных шагов соответствует развернутая версия той же нейронной сети в виде столбца нейронов. Это все равно, что смотреть сценарий или отдельные видеокадры нейронной сети в каждый момент времени. Сеть справа представляет собой будущую версию сети слева. Выходной сигнал скрытого слоя в момент времени (t) подается снова на вход скрытого слоя вместе с входными данными для следующего временного шага (t + 1) справа. И еще раз. На схеме показаны две итерации этого развертывания, всего три столбца нейронов для t = 0, t = 1 и t = 2. Все вертикальные маршруты на этой схеме полностью аналогичны, в них показаны одни и те же нейроны. Они отражают одну и ту же нейронную сеть в разные моменты времени. Такое наглядное представление удобно при демонстрации движения информации по сети в прямом и обратном направлении во время обратного распространения ошибки. Но помните, глядя на эти три развернутые сети: они представляют собой различные моментальные снимки одной и той же сети с тем же набором весов. Изучим внимательнее исходное представление рекуррентной нейронной сети до ее развертывания и покажем взаимосвязи входных сигналов и весов. Отдельные слои этой RNN выглядят так, как показано на рис. 8.5 и 8.6. У всех нейронов скрытого состояния есть по набору весов, применяемых к каждому из элементов каждого из входных векторов, как в обычной сети прямого распространения. Но в этой схеме появился и дополнительный набор обучаемых весов, которые применяются к выходным сигналам скрытых нейронов из предыдущего временного шага. Сеть путем обучения подбирает подходящие веса (важность) предыдущих событий при вводе последовательности токен за токеном.

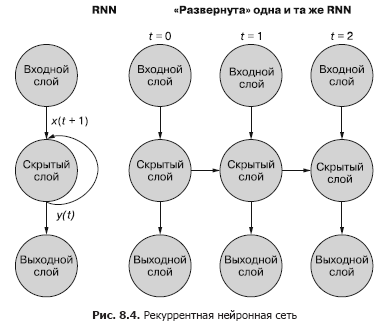
У первого входного сигнала в последовательности нет «прошлого», так что скрытое состояние на шаге t = 0 получает нулевой входной сигнал от себя же с шага t – 1. Можно также для «заполнения» начального значения состояния сначала передать в сеть взаимосвязанные, но отдельные примеры данных, один за другим. Итоговый выходной сигнал каждого примера используется во входном сигнале t = 0 следующего примера данных. В посвященном сохранению состояния разделе в конце данной главы мы расскажем вам, как сохранять больше информации из набора данных с помощью альтернативных методик заполнения.

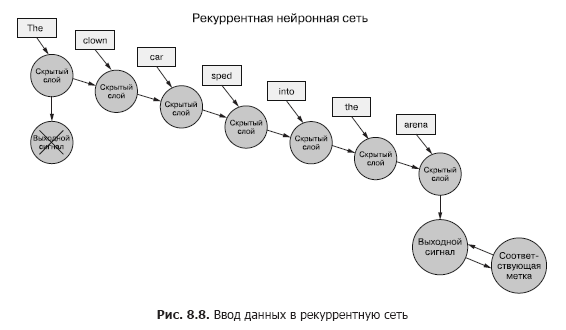
Вернемся к данным: представьте, что у вас есть набор документов, каждый из которых представляет собой маркированный пример. И вместо того, чтобы для каждого выборочного примера передавать набор векторов слов целиком в сверточную нейронную сеть, как в предыдущей главе (рис. 8.7), мы передаем пример данных в RNN по одному токену (рис. 8.8).

Мы передаем вектор слов для первого токена и получаем выходной сигнал нашей рекуррентной нейронной сети. Затем передаем второй токен, а вместе с ним — выходной сигнал от первого! После этого передаем третий токен вместе с выходным сигналом от второго! И так далее. Теперь в нашей нейронной сети существуют понятия «до» и «после», причины и следствия, некое, пусть и расплывчатое, представление о времени (см. рис. 8.8). Теперь наша сеть уже кое-что запоминает! Ну, в известной мере. Осталось выяснить еще несколько вещей. Во-первых, как может происходить обратное распространение ошибки в подобной структуре?

8.1.1. Обратное распространение ошибки во времени

Во всех обсуждавшихся выше сетях существовала искомая метка (целевая переменная), и RNN не исключение. Но у нас отсутствует понятие метки для каждого токена, а есть только одна метка для всех токенов каждого из примеров текста. У нас имеются только метки для примеров документов.

Мы говорим о токенах как входных данных для сети на каждом из временных шагов, но рекуррентные нейронные сети могут так же работать с любыми данными временных рядов. Токены могут быть любыми, дискретными или непрерывными: показания метеостанции, ноты, символы в предложении и т. п.

Здесь мы сначала сравниваем выходной сигнал сети на последнем временном шаге с меткой. Именно это мы и будем (пока что) называть ошибкой, а именно ошибку наша сеть и пытается минимизировать. Но есть небольшое отличие от предыдущих глав. Заданный пример данных разбивается на меньшие части, подаваемые в нейронную сеть последовательно. Однако вместо того, чтобы непосредственно использовать получаемый для каждого из этих «подпримеров» выходной сигнал, мы отправляем его обратно в сеть.

Нас интересует пока что только итоговый выходной сигнал. Каждый из токенов последовательности подается в сеть, и на основе выходного сигнала последнего временного шага (токена) вычисляются потери (рис. 8.9).

Необходимо определить при наличии ошибки для заданного примера, какие веса обновить и насколько. В главе 5 мы рассказали, как производить обратное распространение ошибки по обычной сети. И мы знаем, что величина корректировки веса зависит от его (этого веса) вклада в ошибку. Мы можем подавать по токену из выборочной последовательности на вход сети, вычисляя на основе ее выходного сигнала ошибку для предыдущего временного шага. Тут-то идея обратного распространения ошибки во времени, похоже, все и запутывает. Впрочем, можно просто рассматривать это как процесс с привязкой по времени. На каждом временном шаге токены, начиная с первого при t = 0, подаются по одному на вход расположенного впереди скрытого нейрона — следующий столбец на рис. 8.9. При этом сеть развертывается, раскрывая следующий столбец сети, уже готовый для получения очередного токена в последовательности. Скрытые нейроны развертываются по одному, подобно музыкальной шкатулке или механическому пианино. В конце концов, когда в сеть будут поданы все элементы примеров, развертывать больше будет нечего и мы получим на выходе итоговую метку для интересующей нас целевой переменной, которую можно использовать для вычисления ошибки и корректировки весов. Мы только что прошли весь путь по графу вычислений для этой развернутой сети (unrolled net). Пока что мы считаем входные данные в целом статическими. Можно проследить по всему графу, какой входной сигнал поступает в какой нейрон. А раз мы знаем, как срабатывает какой нейрон, то можем распространить ошибку обратно по цепочке, по тому же пути, точно так же, как и в случае обычной нейронной сети прямого распространения. Для обратного распространения ошибки на предыдущий слой мы воспользуемся цепным правилом. Вместо предыдущего слоя мы распространим ошибку на тот же слой в прошлом, как если бы все развернутые варианты сети были различны (рис. 8.10). Математика расчетов при этом не меняется. Ошибка с последнего шага распространяется обратно. Вычисляется градиент более раннего временного шага относительно более нового. После вычисления всех отдельных градиентов по токенам, вплоть до шага t = 0 для данного примера, изменения агрегируются и применяются к одному набору весов.

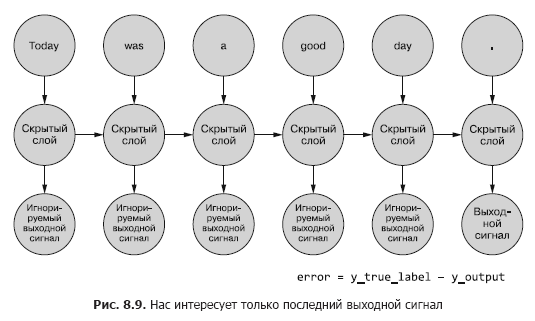
8.1.2. Когда что обновлять

Мы превратили нашу странную RNN в нечто похожее на обычную нейронную сеть прямого распространения, так что обновление весов не должно вызвать затруднений. Впрочем, есть один нюанс. Хитрость в том, что веса обновляются вовсе не в другой ветке нейронной сети. Каждая ветка представляет собой ту же сеть в другие моменты времени. Веса для каждого временного шага одни и те же (см. рис. 8.10).

Простое решение этой проблемы — вычисление поправок для весов на каждом из временных шагов с отсрочкой обновления. В сети прямого распространения все обновления весов вычисляются сразу после вычисления всех градиентов для конкретного входного сигнала. И здесь точно так же, но обновления откладываются, пока мы не доберемся до начального (нулевого) временного шага для конкретного входного примера данных.

В основе расчета градиента должны лежать значения весов, при которых они внесли данный вклад в ошибку. Вот и самая ошеломительная часть: вес на временном шаге t внес некий вклад в ошибку. И тот же вес получает другой входной сигнал на временном шаге t + 1, а значит, вносит уже другой вклад в ошибку.

Можно вычислять различные изменения весов на каждом из временных шагов, суммировать их и затем применять сгруппированные изменения к весам скрытого слоя в качестве последнего шага этапа обучения.

Во всех этих примерах передается отдельный тренировочный пример данных для прямого прохода, а затем производится обратное распространение ошибки. Как и в любой нейронной сети, этот прямой проход по сети можно производить или после каждого тренировочного примера, или в виде батчей. Оказывается, что у пакетного подхода есть и другие преимущества, помимо быстродействия. Но пока что мы будем рассматривать эти процессы с точки зрения отдельных примеров данных, отдельных предложений или документов.

Настоящее волшебство. При обратном распространении ошибки во времени может производиться корректировка отдельного веса в одну сторону на временном шаге t (в зависимости от его реакции на входной сигнал на временном шаге t), а затем в другую сторону на временном шаге t – 1 (в соответствии с тем, как он отреагировал на входной сигнал на временном шаге t – 1) для одного примера данных! Помните, что нейронные сети в целом основаны на минимизации функции потерь вне зависимости от сложности промежуточных шагов. В совокупности сеть оптимизирует эту сложную функцию. Поскольку обновление веса применяется для примера данных однократно, то сеть (если она вообще сходится, конечно) в итоге останавливается на наиболее оптимальном в этом смысле весе для конкретного входного сигнала и конкретного нейрона.

Результаты предыдущих шагов все же важны

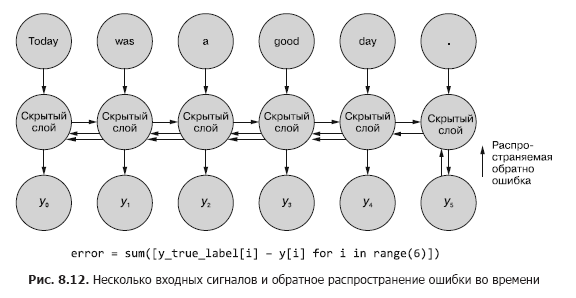
Иногда оказывается важна вся последовательность значений, генерируемая на всех промежуточных временных шагах. В главе 9 мы приведем примеры ситуаций, в которых выходной сигнал конкретного временного шага t ничуть не менее важен, чем выходной сигнал последнего временного шага. На рис. 8.11 приведен способ сбора данных об ошибке для любого временного шага и обратного ее распространения для корректировки всех весов сети.

Этот процесс напоминает обычное обратное распространение ошибки во времени для n временных шагов. В данном случае мы распространяем обратно ошибку из нескольких источников одновременно. Но, как и в первом примере, корректировки весов носят аддитивный характер. Ошибка распространяется с последнего временного шага в начале до первого с суммированием изменений каждого из весов. Затем то же самое происходит с ошибкой, вычисленной на предпоследнем временном шаге с суммированием всех изменений вплоть до t = 0. Этот процесс повторяется, пока мы не дойдем до нулевого временного шага с обратным распространением ошибки для него так, как будто он единственный. Затем суммарные изменения применяются все сразу к соответствующему скрытому слою. На рис. 8.12 видно, как ошибка распространяется от каждого выходного сигнала обратно аж до t = 0, затем агрегируется перед итоговой корректировкой весов. Это основная идея данного раздела. Как и в случае обычной нейронной сети прямого распространения, веса обновляются только после вычисления предлагаемого изменения весов для всего шага обратного распространения ошибки для данного входного сигнала (или набора входных сигналов). В случае RNN обратное распространение ошибки включает обновления вплоть до момента времени t = 0. Обновление весов ранее внесло бы искажения в расчеты градиентов при обратных распространениях ошибок в более ранние моменты времени. Как вы помните, градиенты вычисляются относительно конкретного веса. Если обновить этот вес слишком рано, скажем на временном шаге t, то при вычислении градиента на временном шаге t – 1 значение веса (напомним, что это та же позиция веса в сети) изменится. И при вычислении градиента на основе входного сигнала с временного шага t – 1 расчеты окажутся искаженными. Фактически при этом вес будет штрафоваться (или вознаграждаться) за то, в чем «не виноват»!

Об авторах

Хобсон Лейн (Hobson Lane) обладает 20-летним опытом создания автономных систем, принимающих важные решения в интересах людей. В компании Talentpair Хобсон обучал машины читать и понимать резюме менее предубежденно, чем большинство специалистов по подбору персонала. В Aira он помогал в создании их первого чат-бота, предназначенного для толкования окружающего мира незрячим. Хобсон — страстный поклонник открытости ИИ и ориентированности его на благо общества. Он вносит активный вклад в такие проекты с открытым исходным кодом, как Keras, scikit-learn, PyBrain, PUGNLP и ChatterBot. Сейчас он занимается открытыми научными исследованиями и образовательными проектами для Total Good, включая создание виртуального помощника с открытым исходным кодом. Он опубликовал многочисленные статьи, выступал к лекциями на AIAA, PyCon, PAIS и IEEE и получил несколько патентов в области робототехники и автоматизации.

Ханнес Макс Хапке (Hannes Max Hapke) — инженер-электротехник, ставший инженером в области машинного обучения. В средней школе он увлекся нейронными сетями, когда изучал способы вычислений нейронных сетей на микроконтроллерах. Позднее, в колледже, он применял принципы нейронных сетей к эффективному управлению электростанциями на возобновляемых источниках энергии. Ханнес обожает автоматизировать разработку программного обеспечения и конвейеров машинного обучения. Он соавтор моделей глубокого обучения и конвейеров машинного обучения для сфер подбора персонала, энергетики и здравоохранения. Ханнес выступал с презентациями на тему машинного обучения на разнообразных конференциях, включая OSCON, Open Source Bridge и Hack University.

Коул Ховард (Cole Howard) — специалист по машинному обучению, специалист-практик, занимающийся NLP, и писатель. Вечный искатель закономерностей, он нашел себя в мире искусственных нейронных сетей. В числе его разработок — масштабные рекомендательные системы для торговли через Интернет и передовые нейронные сети для систем машинного интеллекта сверхвысокой размерности (глубокие нейронные сети), занимающие первые места на конкурсах Kaggle. Он выступал с докладами на тему сверточных нейронных сетей, рекуррентных нейронных сетей и их роли в обработке естественного языка на конференциях Open Source Bridge и Hack Universit.