Вооружившись самодельным парсером под покровом ночи я ворвался в онлайн галерею и вынес оттуда почти 50 тысяч картин. Давайте разберем, что интересного с этим можно сделать, используя только классические ML инструменты (осторожно, трафик).
Наивное преобразование
Насколько многие из нас помнят из уроков информатики изображение представляется в виде массива байт, отвечающих за цвет каждого отдельного пикселя. Как правило используется схема RGB, в которой цвет разделен на три составляющие (красный/зеленый/синий), которые при суммировании с черным фоном дают изначальный, воспринимаемый человеком цвет.
Поскольку сейчас для нас все шедевры временно стали лишь массивами чисел на диске, попробуем эти массивы охарактеризовать, построив гистограммы распределения частот интенсивности для каждого канала.
Для вычислений будем использовать numpy, а визуализируем с помощью matplotlib.
# прочитать с диска массив пикселей картины def load_image_by_index(i): image_path = paintings_links.iloc[i].img_path img = cv2.imdecode(np.fromfile(str(Path.cwd()/image_path), np.uint8), cv2.IMREAD_UNCHANGED) return img # посчитать гистограммы по картине def get_hist_data_by_index(img_index): bin_div = 5 img = load_image_by_index(img_index) b, bins= np.histogram(img[:,:,0], bins=255//bin_div, range=(0,255), density=True) g = np.histogram(img[:,:,1], bins=255//bin_div, range=(0,255), density=True)[0] r = np.histogram(img[:,:,2], bins=255//bin_div, range=(0,255), density=True)[0] return bins, r, g, b # строим картину и рядышком с ней гистограммы def plot_image_with_hist_by_index(img_index, height=6): bins, r, g, b = get_hist_data_by_index(img_index) img = load_image_by_index(img_index) fig = plt.figure(constrained_layout=True) if img.shape[0] < img.shape[1]: width_ratios = [3,1] else: width_ratios = [1,1] gs = GridSpec(3, 2, figure=fig, width_ratios = [3,1] ) ax_img = fig.add_subplot(gs[:,0]) ax_r = fig.add_subplot(gs[0, 1]) ax_g = fig.add_subplot(gs[1, 1], sharey=ax_r) ax_b = fig.add_subplot(gs[2, 1], sharey=ax_r) ax_img.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB),aspect = 'equal') ax_img.axis('off') ax_r.bar(bins[:-1], r, width = 5, color='red',alpha=0.7) ax_g.bar(bins[:-1], g, width = 5, color='green',alpha=0.7) ax_b.bar(bins[:-1], b, width = 5, color='blue',alpha=0.7) ax_r.axes.get_xaxis().set_ticks([]) ax_r.axes.get_yaxis().set_ticks([]) ax_g.axes.get_xaxis().set_ticks([]) ax_g.axes.get_yaxis().set_ticks([]) ax_b.axes.get_xaxis().set_ticks([]) ax_b.axes.get_yaxis().set_ticks([]) fig.suptitle("{} - {}".format(paintings_links.iloc[img_index].artist_name, paintings_links.iloc[img_index].picture_name),ha= "left") fig.set_figheight(height) plt.axis('tight') if img.shape[0] < img.shape[1]: fig.set_figwidth(img.shape[1] *height / img.shape[0] *1.25) else: fig.set_figwidth(img.shape[1] *height / img.shape[0] *1.5) plt.show() 



Первая моделька
Соберем все гистограммы в один большой датасет и попробуем поискать в нем некие “аномалии”. Быстрый, удобный и вообще мой самый любимый алгоритм для таких целей — one class svm. Воспользуемся его реализацией из библиотеки sklearn
# пробежимся по всем картинкам в нашей базе, посчитаем гистограммы и соберем из этого датасет res = [] error = [] for img_index in tqdm(range(paintings_links.shape[0])): try: bins, r, g, b = get_hist_data_by_index(img_index) res.append(np.hstack([r,g,b])) except: res.append(np.zeros(153,)) error.append(img_index) np_res = np.vstack(res) # сохраним для дальнейшего использования pd.DataFrame(np_res).to_pickle("histograms.pkl") histograms = pd.read_pickle("histograms.pkl") # обучим модельку. на вход она ожидает от нас предполагаемую долю аномалий. пусть будет 10 аномалий на весь датасет one_class_svm = OneClassSVM(nu=10 / histograms.shape[0], gamma='auto') one_class_svm.fit(histograms[~histograms.index.isin(bad_images)]) # выделим аномалии svm_outliers = one_class_svm.predict(histograms) svm_outliers = np.array([1 if label == -1 else 0 for label in svm_outliers]) # и отобразим их uncommon_images = paintings_links[(svm_outliers ==1) & (~histograms.index.isin(bad_images))].index.values for i in uncommon_images: plot_image_with_hist_by_index(i,4) 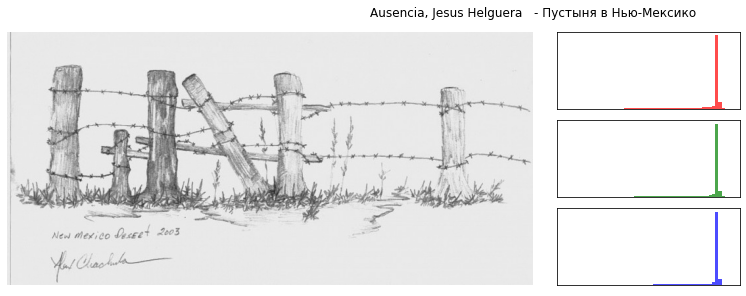




Поиск похожих работ
Отлично, наша модель находит что-то необычное, далекое от всего остального.
А можем ли мы сделать инструмент, который поможет найти близкие по цветовому решению работы?
Сейчас каждая картина характеризуется вектором из 153 значений (потому что при построении гистограммы бил на бины по 5 единиц интенсивности, итого 255/5 = 51 частота для каждого канала).
“Степень похожести” мы можем определить, посчитав расстояния между интересующими нас векторами. Знакомое еще со школы евклидово расстояние здесь будет много внимания уделять длине векторных компонент, а нам бы хотелось уделить больше внимания наборам оттенков, составляющим картину. Здесь нам будет полезна косинусная мера расстояния, широко используемая, например, в задачах анализа текстов. Попробуем применить ее для данной задачи. Реализацию возьмем из библиотеки scipy.
# сделаем инструмент, который поможет найти похожие по цветовой гамме картины from scipy import spatial def find_closest(target_id,n=5): distance_vector = np.apply_along_axis(spatial.distance.cosine, arr=histograms, axis=1, v=histograms.values[target_id]) return np.argsort(distance_vector)[:n] Оригинал:



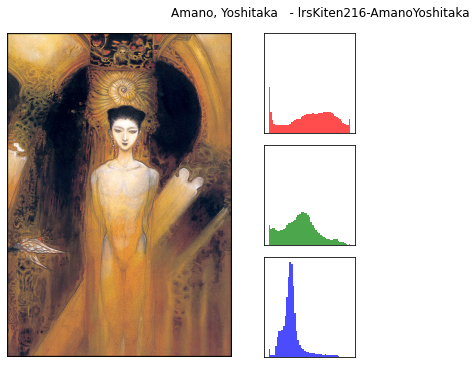
Оригинал:



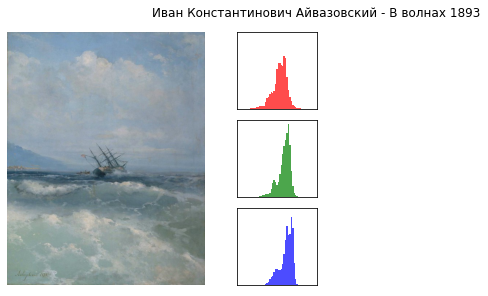
Оригинал:





Цветовые пространства
До этого момента мы с вами работали в цветовом пространстве RGB. Оно весьма удобно для понимания, но далеко не идеально для наших задач.
Посмотрите, например, на грани цветового куба RGB

Выбирать для себя любимое цветовое пространство будем, сравнивая его полезность в решении какой-нибудь человеческой задачи. Давайте, например, вычислять художника по содержимому холста!
Возьмем все доступные цветовые пространства из библиотеки opencv, обучим xgboost на каждом и посмотрим метрики на отложенной выборке.
# функция, которая посчитает нам гистограмму в нужном цветовом пространстве def get_hist_data_by_index_and_colorspace(bgr_img, colorspace): bin_div = 5 img_cvt = cv2.cvtColor(bgr_img, getattr(cv2, colorspace)) c1, bins = np.histogram(img_cvt[:,:,0], bins=255//bin_div, range=(0,255), density=True) c2 = np.histogram(img_cvt[:,:,1], bins=255//bin_div, range=(0,255), density=True)[0] c3 = np.histogram(img_cvt[:,:,2], bins=255//bin_div, range=(0,255), density=True)[0] return bins, c1, c2, c3 # посчитаем гистограммы всех изображений во всех цветовых пространствах all_res = {} all_errors = {} for colorspace in list_of_color_spaces: all_res[colorspace] =[] all_errors[colorspace] =[] for img_index in tqdm(range(paintings_links.shape[0]) ): for colorspace in list_of_color_spaces: try: bgr_img = load_image_by_index(img_index) bins, c1, c2, c3 = get_hist_data_by_index_and_colorspace(bgr_img, colorspace) all_res[colorspace].append(np.hstack([c1, c2, c3])) except: all_res[colorspace].append(np.zeros(153,)) all_errors[colorspace].append(img_index) all_res_np = {} for colorspace in list_of_color_spaces: all_res_np[colorspace] = np.vstack(all_res[colorspace]) res = [] # а теперь для каждого цветового пространства построим модельку for colorspace in tqdm(list_of_color_spaces): temp_df = pd.DataFrame(all_res_np.get(colorspace)) temp_x_train = temp_df[temp_df.index.isin(X_train.index.values)] temp_x_test = temp_df[temp_df.index.isin(X_test.index.values)] xgb=XGBClassifier() xgb.fit(temp_x_train, y_train) current_res = classification_report(y_test, xgb.predict(temp_x_test), labels=None, target_names=None, output_dict=True).get("macro avg") current_res["colorspace"] = colorspace res.append(current_res) pd.DataFrame(res).sort_values(by="f1-score") | precision | recall | f1-score | colorspace |
|---|---|---|---|
| 0.001329 | 0.003663 | 0.001059 | COLOR_BGR2YUV |
| 0.003229 | 0.004689 | 0.001849 | COLOR_BGR2RGB |
| 0.003026 | 0.004131 | 0.001868 | COLOR_BGR2HSV |
| 0.002909 | 0.004578 | 0.001934 | COLOR_BGR2XYZ |
| 0.003545 | 0.004434 | 0.001941 | COLOR_BGR2HLS |
| 0.003922 | 0.004784 | 0.002098 | COLOR_BGR2LAB |
| 0.005118 | 0.004836 | 0.002434 | COLOR_BGR2LUV |
Вот так выглядит срез данного цветового пространства при фиксации одной из осей:
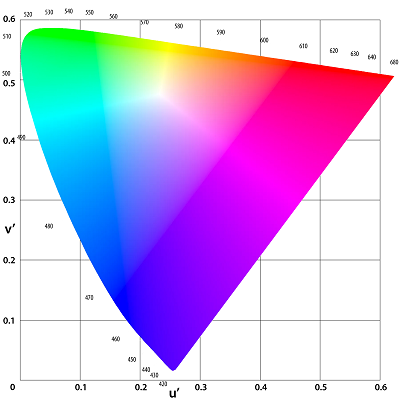
Посмотрим на модельку
После предыдущего шага у нас осталась модель, которая умеет что-то предсказывать.
Давайте посмотрим, чьи работы мы узнаём наиболее точно.
| precision | recall | f1-score | Художник |
|---|---|---|---|
| 0.042553 | 0.019417 | 0.026667 | Илья Ефимович Репин |
| 0.055556 | 0.020000 | 0.029412 | Уильям Меррит Чейз |
| 0.071429 | 0.022222 | 0.033898 | Bonnard, Pierre |
| 0.035461 | 0.035211 | 0.035336 | Джил Элвгрен |
| 0.100000 | 0.021739 | 0.035714 | Жан Огюст Доминик Энгр |
| 0.022814 | 0.224066 | 0.041411 | Пьер Огюст Ренуар |
| 0.100000 | 0.028571 | 0.044444 | Альберт Бирштадт |
| 0.250000 | 0.032258 | 0.057143 | Ханс Зацка |
| 0.030396 | 0.518797 | 0.057428 | Клод Оскар Моне |
| 0.250000 | 0.037037 | 0.064516 | Girotto, Walter |
Возьмем его работы, попросим модель сообщить нам автора и посчитаем частоты
| Предсказанный автор | Количество предсказаний |
|---|---|
| Клод Оскар Моне | 186 |
| Пьер Огюст Ренуар | 171 |
| Винсент Ван Гог | 25 |
| Питер Пауль Рубенс | 19 |
| Гюстав Доре | 17 |



















Цветовой круг Иттена


- Комплиментарные цвета — находящиеся на противоположных частях круга
- Смежные цвета — находящиеся по соседству на круге
- Классическая триада — цвета на вершинах равностороннего треугольника
- Контрастная триада — цвета на вершинах равнобедренного треугольника
- Правило прямоугольника — цвета на вершинах прямоугольника
- Правило квадрата — цвета на вершинах квадрата
Анализируем как художники
Попробуем применить на практике полученные знания. Для начала получим массив цветов, лежащих на цветовом круге, распознав их из картинки.

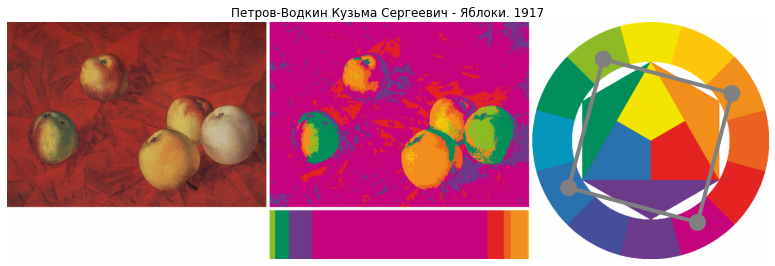
# функция для построения картины и анализа частот по цветовому кругу def plot_composition_analysis(image_index): img = load_image_by_index(image_index) luv_img = cv2.cvtColor(load_image_by_index(image_index), cv2.COLOR_BGR2LUV) closest_colors = np.argmin(euclidean_distances(luv_img.reshape(-1,3),wheel_colors_luv),axis=1) wheel_colors2[closest_colors].reshape(luv_img.shape) color_areas_img = wheel_colors2[closest_colors].reshape(img.shape) v, c = get_image_colors(image_index) # переведем в целочисленные значения и отмасштабируем по ширине картины c_int = (c*img.shape[1]).astype(int) c_int_delta = img.shape[1] - sum(c_int) c_int[np.argmax(c_int)] = c_int[np.argmax(c_int)] + c_int_delta _ = [] for i, vi in enumerate(v): bar_width = c_int[i] _.append(np.tile(wheel_colors2[vi], (150,bar_width,1))) color_bar_img = np.hstack(_) final_image = np.hstack([ np.vstack([img, np.tile(np.array([254,254,254]),(160,img.shape[1],1))]), np.tile(np.array([254,254,254]),(img.shape[0]+160,10,1)), np.vstack([color_areas_img, np.tile(np.array([254,254,254]),(10,img.shape[1],1)), color_bar_img]) ]) h = 12 w = h / final_image.shape[1] * final_image.shape[0] fig = plt.figure(figsize=(h,w)) plt.imshow(cv2.cvtColor(final_image.astype(np.uint8), cv2.COLOR_BGR2RGB),interpolation='nearest', aspect='auto') plt.title("{} - {}".format(paintings_links.iloc[image_index].artist_name, paintings_links.iloc[image_index].picture_name),ha= "center") plt.axis('off'); 




Все комплементарные пары:



Для начала пары:

















На этот раз список наиболее “предсказуемых” художников несколько поменялся, а это значит, что иной подход к анализу позволил нам извлечь еще немного информации из содержимого картины.
| precision | recall | f1-score | Художник |
|---|---|---|---|
| 0.043478 | 0.012195 | 0.019048 | Martin, Henri-Jean-Guillaume |
| 0.032680 | 0.029070 | 0.030769 | Камиль Писсарро |
| 0.166667 | 0.019608 | 0.035088 | Жан-Леон Жером |
| 0.076923 | 0.027778 | 0.040816 | Turner, Joseph Mallord William |
| 0.133333 | 0.024390 | 0.041237 | Poortvliet, Rien |
| 0.100000 | 0.026316 | 0.041667 | Макс Клингер |
| 0.026725 | 0.228216 | 0.047847 | Пьер Огюст Ренуар |
| 0.200000 | 0.028571 | 0.050000 | Brasilier, Andre |
| 0.028745 | 0.639098 | 0.055016 | Клод Оскар Моне |
Заключение
Произведения искусства уникальны и неповторимы. Художники используют множество композиционных приемов, заставляющих нас восхищаться их работами снова и снова.
Цветовое решение — важная, но далеко не единственная составляющая в анализе работ художников.
Многие настоящие искусствоведы посмеются над наивностью проведенного анализа, но все равно проведенной работой я остался доволен. Есть еще несколько идей, до которых пока не дошли руки:
- Применить алгоритмы кластеризации к анализу цветовых решений художников. Наверняка мы смогли бы выделить там интересные группы, отличили бы различные течения в живописи
- Применить алгоритмы кластеризации к отдельным картинам. Поискать “сюжеты”, которые можно определить по цветовому решению. Например в разных кластерах получить пейзажи, портреты и натюрморты
- Поискать не только пары, тройки и квадраты, но и прочие комбинации с круга Иттена
- Перейти от анализа частот к анализу “цветовых пятен”, группируя пиксели по месторасположению
- Найти работы, в которых авторство под сомнением и посмотреть, за кого проголосует модель
P.S.
Данная статья изначально была выпускным проектом для курса по машинному обучению, однако несколько людей рекомендовали превратить ее в материал для Хабра. Надеюсь вам было интересно.
Весь код, использованный в работе, доступен на github.
