Выращиваем ИИ — Генетические алгоритмы: введение

(сгенерированое изображение)

Существует множество способов создать искусственную нейронную сеть или даже "искусственный интеллект". Но все эти способы обескураживают, от части сложностью которую я не до конца понимаю, отчасти от того, что все сводится к математическим формулам.

В таких подходах нет нечего плохого, они помогают решать поставленные перед ними задачи. Но похоже мне очень хочется написать велосипед.

Зачем, что и почему?

Прежде чем мы приступим к основной теме, небольшая предыстория, как меня сюда занесло.
Я долго изучал тему с разных сторон и даже пытался разобраться в работе клеток организма и в частности нейронных клеток.

К моему удивлению, скорей всего ввиду пропуска уроков по биологии, этот удивительный мир держится на элементарных вещах, подобно компьютеру в котором имея в распоряжении 1 и 0 мы можем целыми днями рассматривать гифки с котиками и спорить друг с другом. Только вместо 1 и 0 мы состоим из множества различных клеток которые живут и функционируют на чистой химии и физике. Со стороны может показаться, что они разумны, но это не так.

Нейронная клетка в мозгу +- нечем не отличается от других клеток. Зачастую многие ставят под вопрос, то как передаются сигналы от нейрона к нейрону? Но как по мне, куда более важный вопрос — как формируется нейронная сеть? Как один нейрон находит другой "нужный нейрон"?

Этот вопрос до конца не изучен Axon guidance.

Аксон буквально нанюхивает другой нейрон, на его пути рассыпано множество различных вещей которые его притягивают или отталкивают и за счет этого он двигается к своей цели.

Что влияет на выбор пути:

Нетрины
Эфрины и Eph-рецепторы
Семафорины
Рецепторы: плексины, интегрины, нейропилины;
Участники сигнальной цепочки: CRMP-семейство (CRMP1, CRMP2, CRMP3, CRMP4, CRMP5)

Аксон, как правило, находит только один другой нейрон. Но дендритам одного нейрона могут посылать свои сигналы несколько аксонов. Не редки случаи когда от аксона идет несколько ответвлений.

Симуляция таких процессов будет слишком затратным делом и нам это особо не нужно. Самое главное это конечная структура нейронной сети. Возможно ли как-то вырастить ее, нарисовать точно так как это делает природа?

Когда я понял, что страдаю фигней, решил начать гуглить — клеточные автоматы и генетически выращенные нейронные сети. Спойлер — есть подходы обучения нейронных сетей за счет генетических алгоритмов и где-то пишут, что это крутая смесь.

Вобщем сейчас я остановился на генетических алгоритмах и изучаю их в свободное время. Возможно это все так же приведет в тупик, но это интересно.

Генетические алгоритмы

Сегодня мы рассмотрим базис генетических алгоритмов и напишем простенькую программку.

Термин «генетический алгоритм» относится к конкретному алгоритму, реализованному особым образом для решения определенных проблем. Хотя формальный генетический алгоритм сам по себе послужит основой для примеров, которые мы создадим в этой статье, нам не нужно беспокоиться о реализации алгоритма с идеальной точностью, учитывая, что мы ищем творческое использование эволюционных теорий.

Начнем с традиционного компьютерного генетического алгоритма. Этот алгоритм был разработан для решения задач, в которых пространство решения настолько велико, что алгоритм «грубой силы» просто занял бы слишком много времени. Например: я думаю о числе. Число от одного до одного миллиарда. Сколько времени вам потребуется, чтобы угадать это? Решение проблемы с помощью «грубой силы» относится к процессу проверки каждого возможного решения. Это один? Это два? Это три? Это четыре? И так, и так далее. Хотя удача играет здесь важную роль, с грубой силой мы будем ожидаем годы, пока вы сосчитаете до одного миллиарда. Однако что, если бы я мог сказать вам, был ли ваш ответ хорошим или плохим? Тепло или холодно? Жарко? Супер, супер холодно? Если бы вы могли оценить, насколько «подходит» предположение, вы могли бы выбрать другие числа ближе к этому предположению и быстрее найти ответ. Ваш ответ может развиваться.

Почему генетические алгоритмы?

Хотя компьютерное моделирование эволюционных процессов восходит к 1950-м годам, большая часть того, что мы сегодня называем генетическими алгоритмами (также известными как «GA»), была разработана Джоном Холландом, профессором Мичиганского университета, чья книга Adaptation in Natural and Artificial Systems была первая в исследованиях GA. Сегодня все больше генетических алгоритмов являются частью более широкой области исследований, часто называемой «Эволюционные вычисления».

Чтобы проиллюстрировать традиционный генетический алгоритм, мы начнем с обезьян. Нет, не наших эволюционных предков. Мы собираемся начать с некоторых вымышленных обезьян, которые стучат по клавишам с целью напечатать полное собрание сочинений Шекспира. Прямо как мои коллеги со своей Java, потряхивая ножкой весь день и регулируя кондиционер с окном.

«Теорема о бесконечной обезьяне» сформулирована следующим образом: Обезьяна, случайно нажимающая клавиши на пишущей машинке, в конечном итоге напечатает все произведения Шекспира (учитывая бесконечное количество времени). Проблема этой теории заключается в том, что вероятность того, что указанная обезьяна действительно напечатала Шекспира, настолько мала, что даже если бы эта обезьяна начинала с Большого взрыва, маловероятно, что у нас будет Гамлет к текущему моменту.

Давайте рассмотрим обезьяну по имени Вова. Вова печатает на уменьшенной пишущей машинке, содержащей только двадцать семь символов: двадцать шесть букв и один пробел. Таким образом, вероятность попадания Вовы в любой заданный ключ — одна из двадцати семи.

Давайте рассмотрим фразу «to be or not to be that is the question» (мы упрощаем его от оригинала «to be or not to be: that is the question»). Фраза длиной 39 символов. Если Вова начинает печатать, вероятность того, что он напечатает первый символ правильно — равна 1 к 27. Первых два символа — 1 к 27 * 27. Следовательно, вероятность того, что Вова напишет полную фразу: $$

Что равно 1 к 66,555,937,033,867,822,607,895,549,241,096,482,953,017,615,834,735,226,163.

Даже если Вова — сможет печатать миллион случайных фраз в секунду, ему пришлось бы печатать в течение 9 719 096 182 010 563 073 122 (253 593 605 017 лет). (Возраст Вселенной составляет всего 13 750 000 000 лет.)

Смысл всех этих непостижимо больших чисел не в том, чтобы озадачить вас, а в том, чтобы продемонстрировать, что алгоритм грубой силы (перебор каждой случайной фразы) не является разумной стратегией для набора "to be or not to be that is the question". Нам помогут генетические алгоритмы.

Конечно, это глупая задача, ведь мы знаем ответ, а генетические алгоритмы, как правило, используются для поиска неизвестного решения. Но наша задача изучить генетические алгоритмы, Скайнет будем создавать завтра.

Естественный отбор Дарвина

Давайте рассмотрим три основных принципа эволюции Дарвина, которые потребуются при реализации нашего алгоритма. Чтобы естественный отбор происходил так, как это происходит в природе, должны присутствовать все эти три элемента:

Наследственность. Должен быть процесс, с помощью которого дети получают свойства своих родителей. Если существа живут достаточно долго, чтобы размножаться, то их черты передаются их детям в следующем поколении существ.

Вариативность (разнообразие).

Должно быть некоторое разнообразие в популяции, или что-то, что его привносит. Например, скажем, есть популяция жуков, в которой все жуки абсолютно одинаковы: одного цвета, одинакового размера, того же размаха крыльев, одинакового всего. Без какого-либо разнообразия в популяции дети всегда будут идентичны родителям и друг другу. Новые комбинации черт никогда не возникнут, и ничто не развивается.

Селекция (выборка). Должен существовать механизм, с помощью которого некоторые представители населения имеют возможность быть родителями и передавать свою генетическую информацию. Обычно это называют «выживанием наиболее приспособленных». Например, популяцию газелей, каждый день гоняют львы. Более быстрые газели с большей вероятностью избегают львов и, следовательно, с большей вероятностью живут дольше, имея возможность размножаться и передавать свои гены детям. Однако термин «наиболее подходящий» может вводить в заблуждение. Как правило, мы ассоциируем это с больше, быстрее или сильнее. В некоторых случаях, это правда, но естественный отбор основывается на том принципе, что некоторые черты лучше приспособлены к среде обитания и следовательно, от них зависит вероятность выживания и размножения. Это не имеет ничего общего с тем, что данное существо «лучше» (в конце концов, это субъективный термин) или более «физически развит». В случае печатающих обезьян более крутая обезьяна — это та, которая набрала фразу ближе к «to be or not to be».

Генетические алгоритмы — создание популяции

В рамках решения задачи о пишущих обезьянах, мы не будем создавать больше обезьян по имени Вова, одного вполне достаточно. Вместо этого, мы сформируем популяцию фраз (коллекцию строк). На этом этапе мы реализуем принцип разнообразия. Допустим наша задача получить строку cat с помощью эволюции и у нас популяция следующего вида:
hug
rid
won

Конечно, в этих трех фразах есть разнообразие, но как не миксуй, получить кошку не получится. Здесь недостаточно разнообразия, чтобы найти оптимальное решение. Однако, если бы мы имели популяцию из тысяч фраз, все полученные случайным образом, то есть вероятность, что по крайней мере один вариант в популяции будет иметь символ "c" в качестве первого символа, один будет иметь "a" в качестве второго, а один "a" в качестве третьего. Большая часть населения, скорее всего, даст нам достаточно разнообразия, чтобы сгенерировать нужную фразу (чуть позже мы введем еще один механизм для регулирования разнообразия).

Таким образом, первый шаг — создание случайной популяции.

Генотип и Фенотип

Данные которыми мы оперируем, передаем из поколения в поколение, являются генотипом. Фенотипом же является представлением этих данных.

То каким образом записывать данные и представлять их зависит от конкретной задачи. В нашем случае, с текстом от обезьянок, особой разницы между генотипом и фенотипом нет. Разве, что мы можем записать символ в виде его ANSI кода в произвольный массив с названием genes.
Наша начальная популяция будет состоять из генерированных случайным образом генотипов — генов — ДНК. Тут уж я не биолог, +- в рамках того, что мы делаем это все одно и то же.

Генетические алгоритмы — селекция

Селекция — наука о создании новых и улучшении существующих пород домашних животных, сортов культурных растений и штаммов микроорганизмов

В нашем случае мы можем разбить селекцию на две части.

1. Оценка пригодности

Пригодность, приспособленность, годность, соответствие. Я черпаю информацию из англ источников и там это называется fitness, от fit.

Для правильного функционирования нашего генетического алгоритма нам необходима так называемая функция пригодности (Fitness function). Функция производит числовую оценку, для определения пригодности конкретного индивидуума. В реальном мире, существа просто выживают или нет. Но в случае традиционного генетического алгоритма, где мы пытаемся выработать оптимальное решение проблемы, мы должны иметь возможность дать численную оценку.

В случае с нашей задачей, мы должны оценивать правильность слов. Например для cat наиболее подходящий вариант будет car:

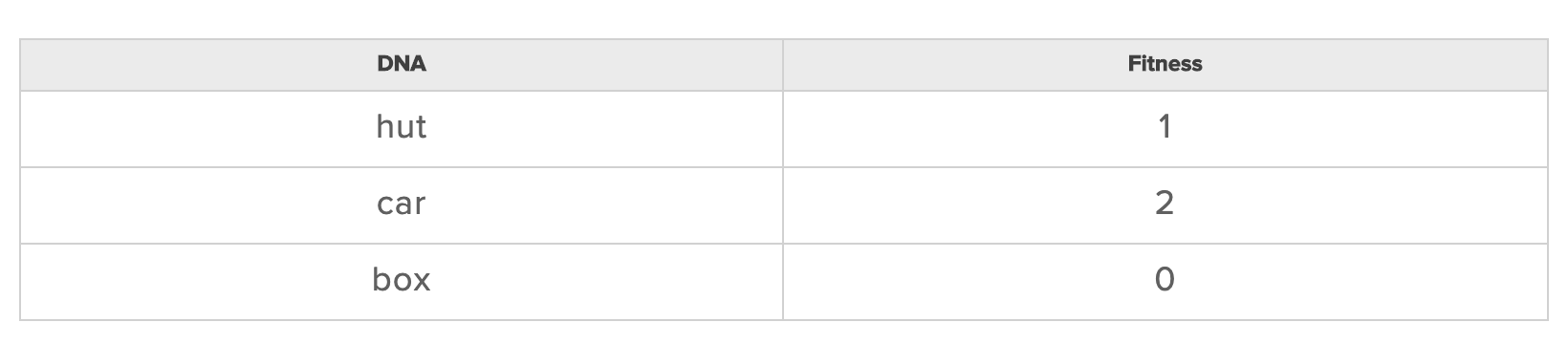
2. Тиндер (пул спаривания)

После того как мы оценили нашу популяцию, пора начинать играть свадьбы.

Здесь можно использовать несколько разных подходов. Например, мы могли бы использовать так называемый элитарный метод: "Какие два члена населения набрали наибольшее количество баллов? Вы двое сделаете всех детей для следующего поколения".

Это один из самых простых подходов, но в таком случае мы потеряем разнообразие. Если два члена населения (из возможно тысяч) являются единственными доступными для размножения, у следующего поколения будет мало разнообразия, и это может замедлить эволюционный процесс. Так же мы могли бы взять половину популяции, например первые 500 из 1000. Это также очень просто сделать, но такой подход не даст оптимальных результатов. В этом случае у элементов с высокими показателями будет такой же шанс быть выбранным в качестве родителя, как и у средних. И почему обезьянка номер 500 имеет возможность воспроизведения, а номер 501 уже нет?

Лучшее решение для нашего тиндера будет использование вероятностного метода, который мы назовем «колесом фортуны» (также известным как «рулетка»). Чтобы проиллюстрировать этот метод, давайте рассмотрим простой пример, где у нас есть совокупность из пяти элементов, каждый из которых имеет оценку:

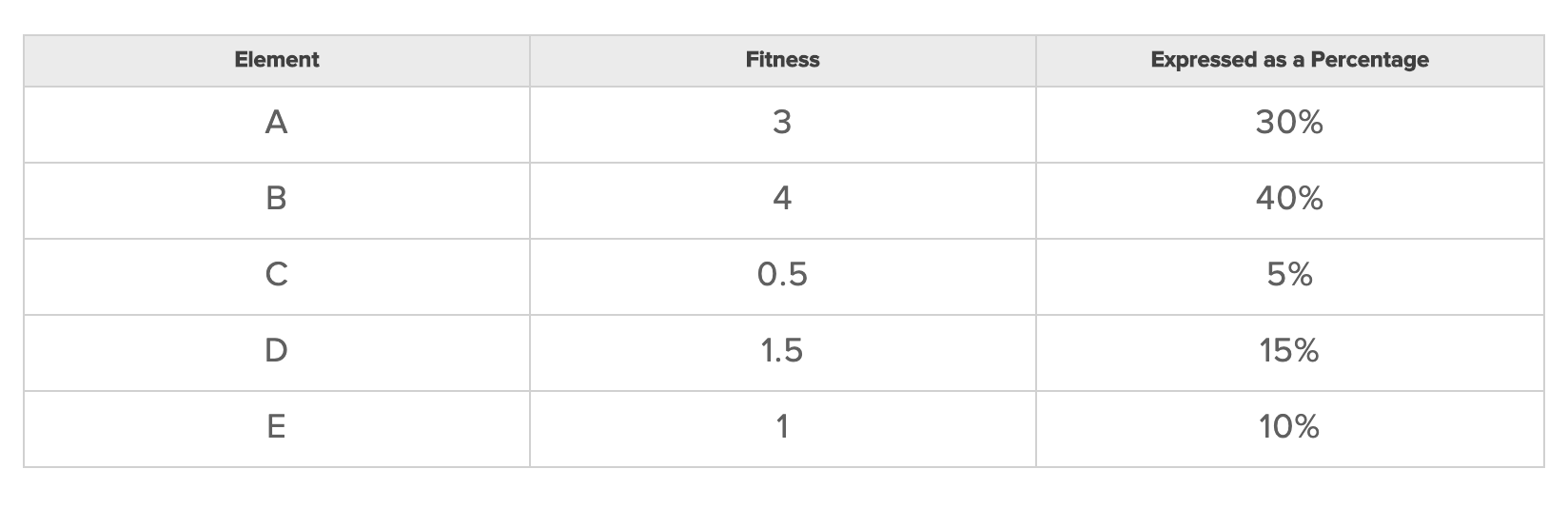
Наша рулетка будет выглядеть следующим образом:

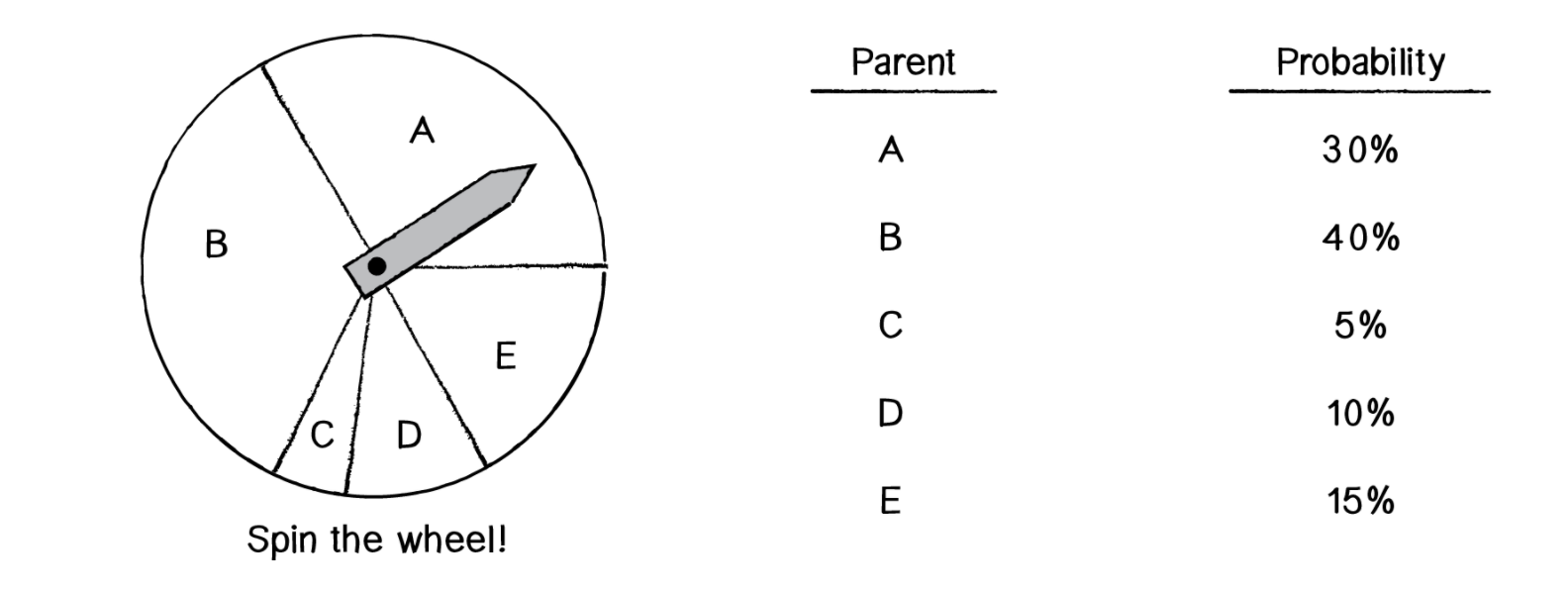
Как мы видим, B имеет наибольший шанс. Но и самые маленькие, такие как C не лишены шанса вовсе. Частенько у элементов с низкой оценкой пригодности есть те необходимые и недостающие необходимые части. Например фраза "to be or not to be":

A: to be or not to go
B: to be or not to pi
C: xxxxxxxxxxxxxxxxbe

А и B подходят больше всего, но C содержит необходимую концовку. Поэтому не стоит исключать такие элементы из выборки.

Абсолютно любая части генетического алгоритма в которой присутствует оценка и вероятность, можно реализовать разными подходами. Следует исходить из конкретной задачи. В нашем случае можно обойтись без методов Монте Карло и прочих более сложных для реализации и понимания вещей.

Генетические алгоритмы — репродукция

Заключительная часть генетического алгоритма которая отвечает за получение следующего поколения Вованов. Это поколение перестанет трогать кондиционер каждые 5ть минут. Так же состоит из двух этапов которые следует выделить:

1. Скрещивание (Crossover)

Скрещивание предполагает создание ребенка из генетического кода двух родителей. В случае с обезьянами, давайте предположим, что мы выбрали две фразы из пула спаривания.

Родитель A: FORK
Родитель B: PLAY

Теперь мы должны сделать из этих двоих дочернюю фразу. Возможно, самый очевидный способ (давайте назовем это методом 50/50) — это взять два первых символа из A и вторые два из B, оставив нам:

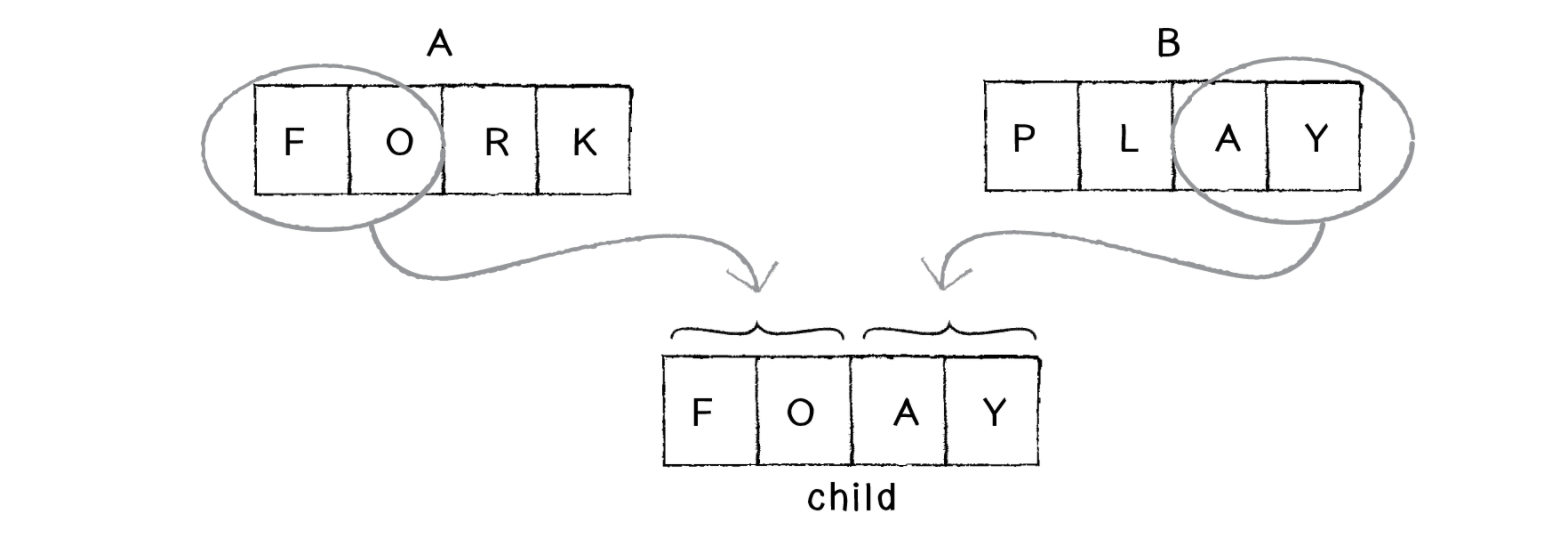
Для большего разнообразия мы можем поручить выбор середины случайности. В таком случае мы можем получить из одних и тех же родителей разные дочерние фразы:

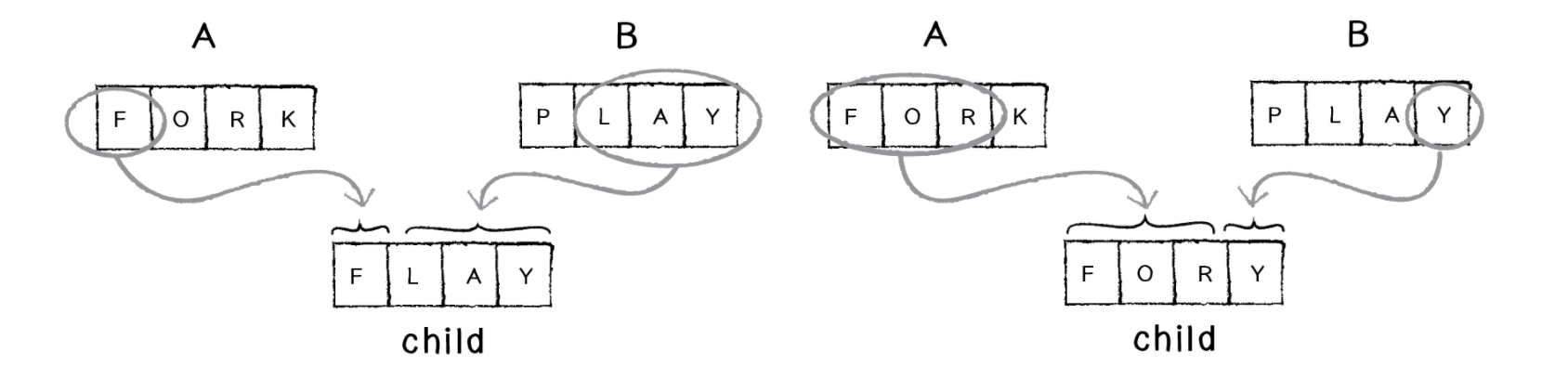
Мы можем пойти дальше и случайным образом выбирать родителя каждого отдельно взятого символа:

Но так как это не мутация, результаты схожи с подходом выше. Для нас нет особой разницы. Как я уже говорил выше, любые действия требующие случайности могут быть реализованы по-разному. В нашем случае такого подхода достаточно.

2. Мутации

Последний процесс перед добавлением нового дочернего элемента в новую популяцию — мутация. Мутация является необязательным шагом, так как в некоторых случаях она не нужна. Но она присутствует в реальном мире и в эволюции Дарвина. Нам необходима мутация для внесения разнообразия по ходу эволюционного процесса. Мы создали начальную популяцию случайным образом, убедившись, что мы начинаем с разнообразных членов популяции. Но по ходу эволюционного процесса мы будем ограничиваться разнообразием популяции которое может с каждым новым поколением уменьшаться. В конце статьи мы проведем эксперимент с различным процентом мутации и убедимся в ее необходимости.

Мутация оценивается в процентах. Допустим мы получили FORY в результате скрещивания, если процент мутации составляет 1%, то это означает, что каждый символ в FORY имеет шанс в 1% быть изменённым другим случайным символом. Это достаточно маленький процент и в 96% случаях мутация не будет происходить. Но если вдруг, то выглядеть это будет следующим образом:

Большой процент мутации, может привести к деградации следующих популяции по отношению к нашему пониманию пригодности, мы не сможем гарантировать "похожесть" детей на родителей.

Давайте подведем итоги по нашему алгоритму и запишем его в виде псевдокода:

SETUP:

Шаг 1: Инициализация, создания случайной популяции из N элементов. Каждый элемент имеет случайную ДНК.

LOOP:

Шаг 2: Селекция, оцениваем каждый элемент популяции и формируем список потенциальных родителей.

Шаг 3: Репродукция. Повторяем N раз:

1. Выбираем двух родителей
2. Скрещиваем
3. Мутируем
4. Добавляем в новую популяцию

Шаг 4. Новая популяция заменяет текущую и повторяем Шаг 2.

Реализация генетического алгоритма

Пора написать реализацию генетического алгоритма. Поскольку у нас есть четкий алгоритм, его реализация будет идти в том же порядке.

Зачастую в подобных вещах используется Python. У нас нет необходимости в специфических библиотеках, поэтому я используя привычный для себя JavaScript.

Если для вас JS не основной язык, думаю не составит труда по аналогии написать в любом другом. Для запуска мы будем использовать Node.js. В коде будет пометка о механизме адаптации, его я дописал, пока писал статью и его мы обсудим ниже. Без него все и так отлично работает :)

Для начала создадим основной класс DNA:

// DNA.js const random = require('./random');  class DNA {     constructor(length, dna = null) {         // Main         this.length = length;         this.genes = dna ? dna.genes : this.getRandomGenes(this.length);          // Additional         this.fitness = 0;     }      getRandomGenes(length) {         return  new Array(length)             .fill(0)                 .map(() => random.getRandomInt(32, 128));     }      // Механизм адаптации который выходит за рамки вышеописанного, его мы обсудим ниже     updateLength(length) {         if (length <= this.genes) {             throw 'Error';         }          this.genes = [...this.genes, this.getRandomGenes(length - this.genes.length)];     } }  module.exports = DNA;

Класс DNA принимает длину фразы, которую хотим получить и набор ДНК, в том случае если это дочерний объект.

getRandomInt возвращает случайное число между 32 и 128 включительно. По факту это английский алфавит в ANSI коде.

// random.js function getRandomInt(min, max) {     min = Math.ceil(min);     max = Math.floor(max);      return Math.floor(Math.random() * (max - min)) + min; // Включительно }  module.exports = {     random: Math.random,     getRandomInt }

DNA.js хранит символы в поле genes. Это своего рода генотип нашей фразы.

Класс популяции будет заниматься основной работой. Созданием популяции, селекции, скрещивания и мутации.

initPopulation() {         this.population = new Array(this.n)             .fill(0)             .map(() => new this.dna(this.target.length));          this.population.forEach((dna) => dna.fitness = this.evaluateFitness(dna));     }

Инициализация популяции начинается с создания пустого массив размером в n, который мы передаем через конструктор. Далее на каждый элемент массива создается элемент популяции со своей случайной ДНК. Чуть ниже, сразу мы оцениванием всю популяцию на пригодность.

evaluateFitness(dna) {         return (dna.genes.reduce((acc, current, index) => {             if (current === this.target.codePointAt(index)) {                 return acc + 1;             }              return acc;         }, 0) / this.target.length);     }

Мы пробегаем по фразе, и подбиваем среднее арифмитическое пригодности фразы. this.target хранится в виде фенотипа строкой. Конечно разумней сразу хранить в виде генотипа, но все для наглядности генетического алгоритма.

getMatingPool() {         let matingPool = [];          this.population.forEach((dna) => {             const n = parseInt(dna.fitness * 100);              matingPool = [...matingPool, ...(new Array(n).fill(dna))];         });          return matingPool;     }

Прекрасный колхозный метод создания рулетки на основе подхода, который мы рассматривали выше. Берем процент пригодности конкретного элемента, создаем такое же количество его клонов и помещаем в массив. Затем когда мы будем выбирать случайным образом элемент из массива, мы будем с той же вероятностью выбирать данный элемент.

findRandomParent(matingPool) {         return matingPool[random.getRandomInt(0, matingPool.length)];     }

Скрещиваем двух родителей

crossover(dna1, dna2) {         const child = new this.dna(this.target.length);          const midpoint = random.getRandomInt(0, dna1.genes.length);          for (let i = 0; i < dna1.genes.length; i++) {             if (i > midpoint) {                 child.genes[i] = dna1.genes[i];             }             else {                 child.genes[i] = dna2.genes[i];             }         }          return child;     }

Случайным образом выбраем середину, часть берем от первого родителя, часть от второго и ребенок готов.

Остается только провести мутацию:

mutation(dna) {         const mutatedDNA = new this.dna(this.target.length, dna);          // Пробегаемся по всем символам фразы         for (let i = 0; i < dna.genes.length; i++) {             if (random.random() < this.mutationRate) {                 // Записываем новый случайный символ                 mutatedDNA.genes[i] = random.getRandomInt(32, 128);             }         }          return mutatedDNA;     }

Все очень просто, мы пробегаемся по всем символам фразы и в соответствии с процентом мутации заменяем или не заменяем символ на новый случайный символ.

Полный код класс популяции:

// Population.js const random = require('./random');  class Population {     constructor(target, dna, n = 100, mutationRate = 0.01, adaptive = false, adaptiveThreshold = 0.6, cutLength = 5) {         this.endTarget = target; // String         this.adaptive = adaptive;         this.adaptiveThreshold = adaptiveThreshold;         this.cutLength = cutLength;         this.target = this.adaptive ? target.substr(0, this.cutLength) : target; // String         this.dna = dna;         this.n = n;         this.mutationRate = mutationRate;         this.population = []         this.populationInfo = {             generationCount: 0         };          this.initPopulation();     }      initPopulation() {         this.population = new Array(this.n)             .fill(0)             .map(() => new this.dna(this.target.length));          this.population.forEach((dna) => dna.fitness = this.evaluateFitness(dna));     }      // Механизм адаптации который выходит за рамки вышеописанного, его мы обсудим ниже     updateDNA(target) {         this.target = target;          this.population.forEach((dna) => {             dna.updateLength(target.length);         });     }      getPopulationInfo() {         let statsFitness1 = 0;          return {             generationCount: this.populationInfo.generationCount,             averageFitness: this.population                 .reduce((acc, current) => {                     if (this.target === String.fromCharCode.apply(this, current.genes)) {                         statsFitness1 += 1;                     }                      return acc + current.fitness                 }, 0) / this.population.length,             statsFitness1         }     }      getMatingPool() {         let matingPool = [];          this.population.forEach((dna) => {             const n = parseInt(dna.fitness * 100);              matingPool = [...matingPool, ...(new Array(n).fill(dna))];         });          return matingPool;     }      evaluateFitness(dna) {         return (dna.genes.reduce((acc, current, index) => {             if (current === this.target.codePointAt(index)) {                 return acc + 1;             }              return acc;         }, 0) / this.target.length);     }      findRandomParent(matingPool) {         return matingPool[random.getRandomInt(0, matingPool.length)];     }      nextGeneration() {         let matingPool = this.getMatingPool();          this.population.forEach((_, index) => {             const parentA = this.findRandomParent(matingPool);             let parentB = null;              while (!parentB || (parentB === parentA)) {                 parentB = this.findRandomParent(matingPool);             }              let child = this.crossover(parentA, parentB);              child = this.mutation(child);             child.fitness = this.evaluateFitness(child)              this.population[index] = child;         });          this.populationInfo.generationCount += 1;          // Механизм адаптации который выходит за рамки вышеописанного, его мы обсудим ниже         if (this.adaptive && this.target !== this.endTarget) {             if (this.getPopulationInfo().averageFitness >= this.adaptiveThreshold) {                 this.updateDNA(this.endTarget.substr(0, this.target.length + this.cutLength));             }         }     }      crossover(dna1, dna2) {         const child = new this.dna(this.target.length);          // Picking a random “midpoint” in the genes array         const midpoint = random.getRandomInt(0, dna1.genes.length);          for (let i = 0; i < dna1.genes.length; i++) {             // Before midpoint copy genes from one parent, after midpoint copy genes from the other parent             if (i > midpoint) {                 child.genes[i] = dna1.genes[i];             }             else {                 child.genes[i] = dna2.genes[i];             }         }          return child;     }      mutation(dna) {         const mutatedDNA = new this.dna(this.target.length, dna);          // Looking at each gene in the array         for (let i = 0; i < dna.genes.length; i++) {             if (random.random() < this.mutationRate) {                 // Mutation, a new random character                 mutatedDNA.genes[i] = random.getRandomInt(32, 128);             }         }          return mutatedDNA;     } }  module.exports = Population;

Прежде чем начать экспериментировать с нашим генетическим алгоритмом, необходимо обзавестись визуализацией. Обычно это не самая простая задача в машинном обучении, но в нашем случае все довольно просто. Так как это Node.js и заморачиваться с WebGL особо желания нет, пришлось поискать, что-то, что может работать со стандартным выводом — консолью.

К счастью существует такой вот инструмент blessed-contrib который позволяет создавать динамические дашборды.

Нас интересуют графики, их будет два. Один показывающий общую пригодность колонии, а второй количество верных результатов.

Небольшая обертка для удобства, которую мы будем использовать для отображения графиков

// Log.js const blessed = require('blessed'); const contrib = require('blessed-contrib');  class Log {     constructor(rows, cols) {         this.lines = [];         this.screen = blessed.screen();          this.grid = new contrib.grid({             rows,             cols,             screen: this.screen         });          this.screen.on('resize', () => {             this.lines.forEach((line) => {                 line.emit('attach');             })         });          this.screen.key(['escape', 'q', 'C-c'], function(ch, key) {             return process.exit(0);         });     }      addLine(x, label, row, col) {         const line = this.grid.set(row, col, 1, 1, contrib.line, {             label,             style: {                 line: "yellow",                 text: "green",                 baseline: "black"             },             xLabelPadding: 3,             xPadding: 5         });          this.screen.append(line);          line.setData([{             x: x,             y: x.map(v => v * 100)         }]);          return this.lines.push(line) - 1;     }      updateLineData(index, x) {         this.lines[index]             .setData([{                 x,                 y: x             }]         );     }      render() {         this.screen.render();     } }  module.exports = Log;

Для получения этих данных я добавил метод в класс популяции, который возвращает номер поколения, средний уровень пригодности и количество 100% совпадений.

getPopulationInfo() {         let statsFitness1 = 0;          return {             generationCount: this.populationInfo.generationCount,             averageFitness: this.population                 .reduce((acc, current) => {                     if (this.target === String.fromCharCode.apply(this, current.genes)) {                         statsFitness1 += 1;                     }                      return acc + current.fitness                 }, 0) / this.population.length,             statsFitness1         }     }

Тестирование

И так, давайте пробовать нашу поделку.

// index.js const DNA = require('./DNA'); const Population = require('./Population'); const Log = require('./Log'); const contrib = require('blessed-contrib');  // Код для дашбоарда в консоле const log = new Log(2, 2); const statsFitnessAverageIndex = log.addLine([], 'Fitness', 0, 0); const statsFitness1Index = log.addLine([], 'Fitness 1', 0, 1); const screenLog = log.grid.set(1, 1, 1, 1, contrib.log, {     label: 'logs' });  const TARGET = 'Hello Habr!'; const GENERATIONS = 1000; const POPULATION_NUMBER = 150; const MUTATION_RATE = 0.01;  const population = new Population(TARGET, DNA, POPULATION_NUMBER, MUTATION_RATE);  // Для сбора статистики const statsFitnessAverage = []; const statsFitness1 = [];

Самое интересное это создание популяции, мы передаем необходимые параметры зарание объявив их как константы.

// index.js ...  function main() {     population.nextGeneration();      const stats = population.getPopulationInfo();     statsFitnessAverage.push(stats.averageFitness);     statsFitness1.push(stats.statsFitness1); }

Данная функция создает новую популяцию и записывает статистику в массив. На основе этого массива, мы постоим графики.

function update() {     log.updateLineData(statsFitnessAverageIndex, statsFitnessAverage);     log.updateLineData(statsFitness1Index, statsFitness1); }  function sync() {     for (let i = 0; i < GENERATIONS; i++) {         main();     }      update();      log.render(); }  sync();  screenLog.log(`${population.endTarget} : ${population.target}`)

sync делает необходимое количество поколений и отображает график. Асинхронный вариант может пригодиться, когда это занимает слишком много времени и хочется следить за процессом:

function async() {     setInterval(() => {         main();         update();         log.render();     }, 10) }

Результат выполнения кода выше:

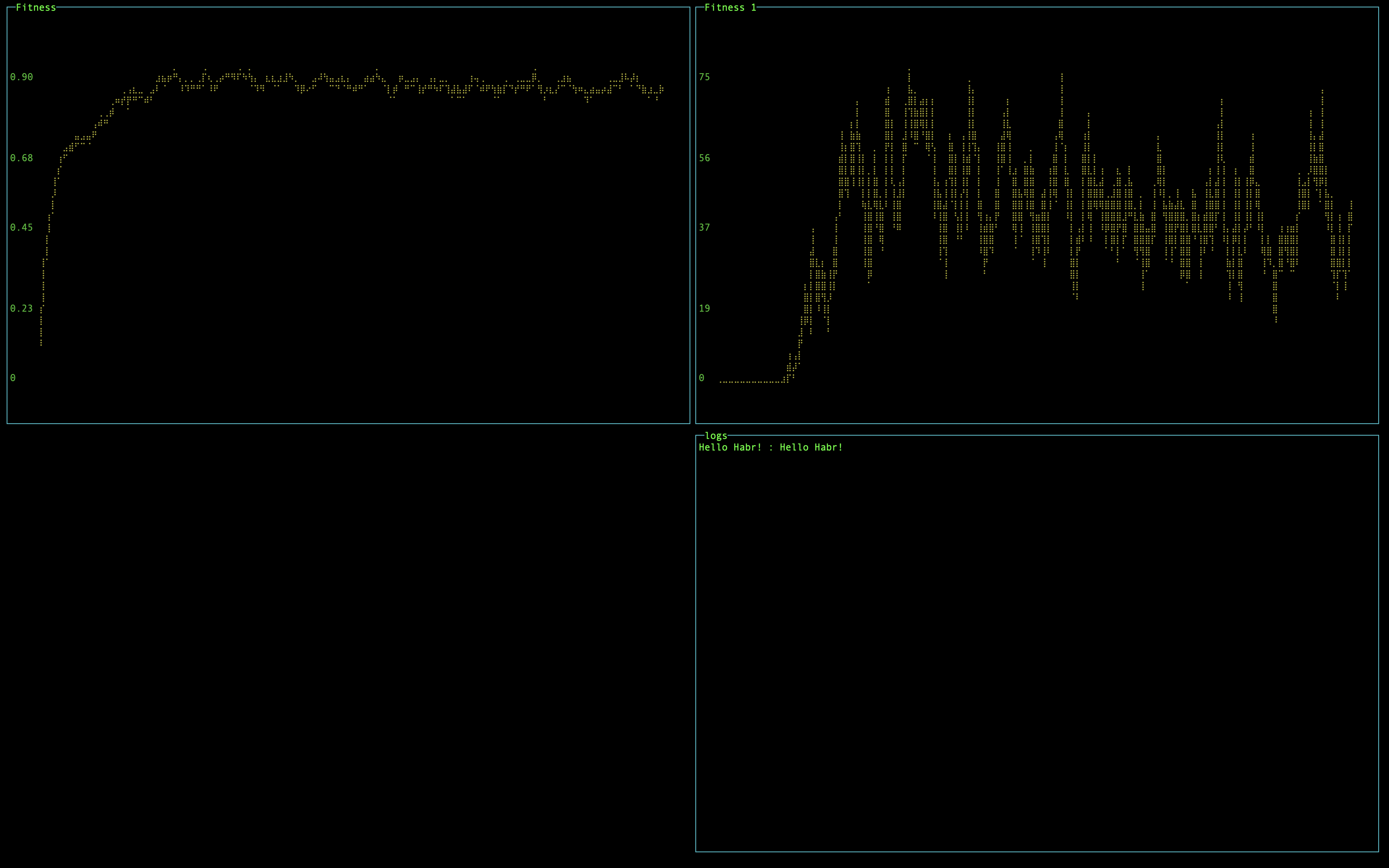
Как мы видим, практически сразу мы получаем 90% рост пригодности, который сохраняется на протяжении многих поколений и не подходит к 100% за счет процесса мутации.
Показатель Fintess 1, это количество 100% подходящих элементов в популяции. Есть некоторые скачки от 20 до 75 на поколение.

Давайте попробуем увеличить фразу. Hello Habr! слишком маленькая фраза и алгоритму она дается очень легко. To be or not to be:

Хороший результат, но правда первый запус дал всего один правильный ответ на 1000 поколений. Чем длинней фраза, тем возможно больше поколений необходимо для достижения правильного решения.

Увеличение количества поколений особо не влияет на результат:

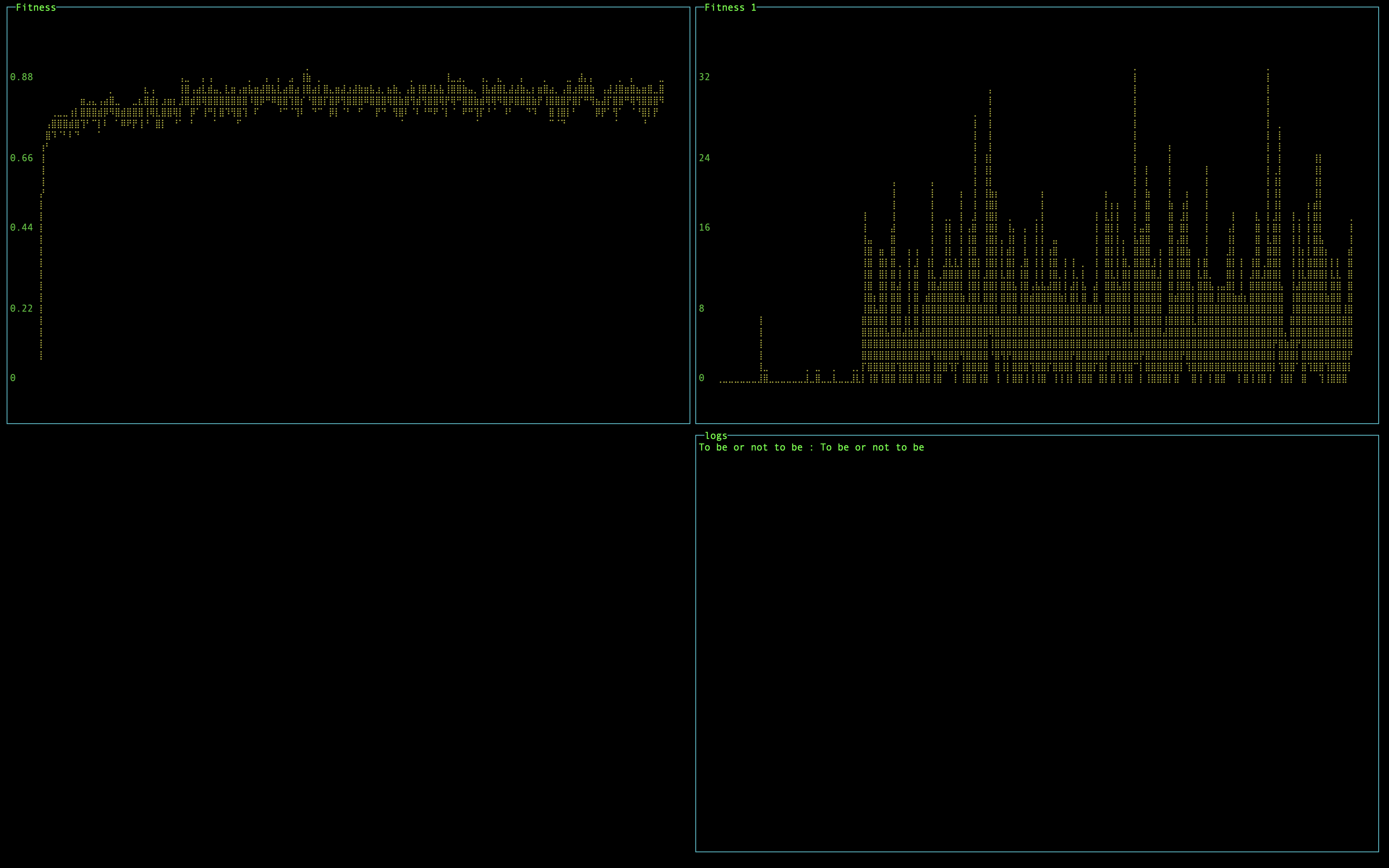
Что если мы попробуем увеличить шанс мутации, с 0.1% до 1%?

При тех же остальных параметрах, результативность упала с 80% до 31-33%. Поколения слишком сильно мутируют и это не дает популяции развиваться в нужном направлении.

Адаптация

Одним из способов улучшить показатель для более длинного текста может быть механизм адаптации. Честно признаюсь, я не изучал его в плане того как он работает в природе, но я пошел логичным путем.

Если более короткие фразы дают быстре и хорошие результаты, быть может стоит бить более длинные фразы на мелкие? По мере роста процента пригодности популяции, мы будем стрессовать ее новыми данными.

И кстати это называется Адаптивные генетические алгоритмы. Полюбому стырили идею у меня.

В коде который я писал выше, уже есть возможность адаптивного подхода. Нужно лишь передать дополнительно 3 новых параметра: adaptive — использовать адаптивный подход, adaptiveThreshold — процент пригодности для удлинения фразы, cutLength — по сколько символов добавлять.

Удвоим фразу:

const TARGET = 'To be or not to be To be or not to be'; const GENERATIONS = 1000; const POPULATION_NUMBER = 150; const MUTATION_RATE = 0.01;  const population = new Population(TARGET, DNA, POPULATION_NUMBER, MUTATION_RATE, true, 0.5, 7);

На графике отчетливо видно зубцы, это момент когда задавалась новая цель и пригодность популяции падала. В данном случае за 1000 поколений, мы не получили правильного решения. Остается только играться с параметрами, может натравить генетический алгоритм на генетический алгоритм для подбора нужных параметров?

Заключение

Мы рассмотрели самый базис генетических алгоритмов на очень простом примере. Но даже тут есть много чего улучшить. Все те места где мы делаем генерацию случайных чисел можно заменить на методы Монте Карло которые так же используются для симуляции различных сложных процессов. Изменить алгоритм выбора родителей и механизм скрещивания двух разных ДНК. Сделать плавающий процент по ипотеке мутации, ведь иногда она полезна, а иногда мешает получить 100% результат.

Генетические алгоритмы способны решать более практические задачи, оптимизации, поиска.

Генеративное исскуство:

Пример с умными ракетами:

Симуляция эволюции экосистемы:

И конечно же обучение нейронных сетей за счет генетических алгоритмов.

Подобные решения рассмотрим в следующей статье. В мое поле зрения еще попал вроде как язык https://processing.org/ и фреймворк HYPE на котором творят много интересного. Постараюсь поиграться с ними.