Практический пример: машинное обучение без учителя, часть 2 — кластеризация методом k средних
В этом разделе будет представлен, пожалуй, самый простой из алгоритмов машинного обучения без учителя — кластеризация методом k средних. Алгоритм анализирует непомеченные образцы и пытается объединить их в кластеры. Поясним, что k в «методе k средних» представляет количество кластеров, на которые предполагается разбить данные.
Алгоритм распределяет образцы на заранее заданное количество кластеров, используя метрики расстояния, сходные с метриками алгоритма кластеризации k ближайших соседей. Каждый кластер группируется вокруг центроида — центральной точки кластера. Изначально алгоритм выбирает k случайных центроидов среди образцов набора данных, после чего остальные образцы распределяются по кластерам с ближайшим центроидом. Далее выполняется итеративный пересчет центроидов, а образцы перераспределяются по кластерам, пока для всех кластеров расстояние от заданного центроида до образцов, входящих в его кластер, не будет минимизировано. В результате выполнения алгоритма формируется одномерный массив меток, обозначающих кластер, к которому относится каждый образец, а также двумерный массив центроидов, представляющих центр каждого кластера.
Набор данных Iris
Поработаем с популярным набором данных Iris, входящим в поставку scikit-learn. Этот набор часто анализируется при классификации и кластеризации. И хотя набор данных помечен, мы не будем использовать эти метки, чтобы продемонстрировать кластеризацию. Затем метки будут использованы для определения того, насколько хорошо алгоритм k средних выполняет кластеризацию образцов.
Набор данных Iris относится к «игрушечным» наборам данных, поскольку состоит только из 150 образцов и четырех признаков. Набор данных описывает 50 образцов трех видов цветов ириса — Iris setosa, Iris versicolor и Iris virginica (см. фотографии ниже). Признаки образцов: длина наружной доли околоцветника (sepal length), ширина наружной доли околоцветника (sepal width), длина внутренней доли околоцветника (petal length) и ширина внутренней доли околоцветника (petal width), измеряемые в сантиметрах.


14.7.1. Загрузка набора данных Iris
Запустите IPython командой ipython --matplotlib, после чего воспользуйтесь функцией load_iris модуля sklearn.datasets для получения объекта Bunch с набором данных:
In [1]: from sklearn.datasets import load_iris In [2]: iris = load_iris()Атрибут DESCR объекта Bunch показывает, что набор данных состоит из 150 образцов (Number of Instances), каждый из которых обладает четырьмя признаками (Number of Attributes). В наборе данных нет отсутствующих значений. Образцы классифицируются целыми числами 0, 1 и 2, представляющими Iris setosa, Iris versicolor и Iris virginica соответственно. Проигнорируем метки и поручим определение классов образцов алгоритму кластеризации методом k средних. Ключевая информация DESCR выделена жирным шрифтом:
In [3]: print(iris.DESCR) .. _iris_dataset: Iris plants dataset -------------------- **Data Set Characteristics:** :Number of Instances: 150 (50 in each of three classes) :Number of Attributes: 4 numeric, predictive attributes and the class :Attribute Information: - sepal length in cm - sepal width in cm - petal length in cm - petal width in cm - class: - Iris-Setosa - Iris-Versicolour - Iris-Virginica :Summary Statistics: ============== ==== ==== ======= ===== ==================== Min Max Mean SD Class Correlation ============== ==== ==== ======= ===== ==================== sepal length: 4.3 7.9 5.84 0.83 0.7826 sepal width: 2.0 4.4 3.05 0.43 -0.4194 petal length: 1.0 6.9 3.76 1.76 0.9490 (high!) petal width: 0.1 2.5 1.20 0.76 0.9565 (high!) ============== ==== ==== ======= ===== ==================== :Missing Attribute Values: None :Class Distribution: 33.3% for each of 3 classes. :Creator: R.A. Fisher :Donor: Michael Marshall (MARSHALL%PLU@io.arc.nasa.gov) :Date: July, 1988 ...Проверка количества образцов, признаков и целевых значений
Количество образцов и признаков можно узнать из атрибута shape массива data, а количество целевых значений — из атрибута shape массива target:
In [4]: iris.data.shape Out[4]: (150, 4) In [5]: iris.target.shape Out[5]: (150,)Массив target_names содержит имена числовых меток массива. Выражение target — dtype='<U10' означает, что его элементами являются строки длиной не более 10 символов:
In [6]: iris.target_names Out[6]: array(['setosa', 'versicolor', 'virginica'], dtype='<U10')Массив feature_names содержит список строковых имен для каждого столбца в массиве data:
In [7]: iris.feature_names Out[7]: ['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']14.7.2. Исследование набора данных Iris: описательная статистика в Pandas
Используем коллекцию DataFrame для исследования набора данных Iris. Как и в случае с набором данных California Housing, зададим параметры pandas для форматирования столбцового вывода:
In [8]: import pandas as pd In [9]: pd.set_option('max_columns', 5) In [10]: pd.set_option('display.width', None)Создадим коллекцию DataFrame с содержимым массива data, используя содержимое массива feature_names как имена столбцов:
In [11]: iris_df = pd.DataFrame(iris.data, columns=iris.feature_names)Затем добавим столбец с названием вида для каждого из образцов. Трансформация списка в следующем фрагменте использует каждое значение в массиве target для поиска соответствующего названия в массиве target_names:
In [12]: iris_df['species'] = [iris.target_names[i] for i in iris.target]Воспользуемся pandas для идентификации нескольких образцов. Как и прежде, если pandas выводит справа от имени столбца, это означает, что в выводе остаются столбцы, которые будут выведены ниже:
In [13]: iris_df.head() Out[13]: sepal length (cm) sepal width (cm) petal length (cm) 0 5.1 3.5 1.4 1 4.9 3.0 1.4 2 4.7 3.2 1.3 3 4.6 3.1 1.5 4 5.0 3.6 1.4 petal width (cm) species 0 0.2 setosa 1 0.2 setosa 2 0.2 setosa 3 0.2 setosa 4 0.2 setosaВычислим некоторые показатели описательной статистики для числовых столбцов:
In [14]: pd.set_option('precision', 2) In [15]: iris_df.describe() Out[15]: sepal length (cm) sepal width (cm) petal length (cm) petal width (cm) count 150.00 150.00 150.00 150.00 mean 5.84 3.06 3.76 1.20 std 0.83 0.44 1.77 0.76 min 4.30 2.00 1.00 0.10 25% 5.10 2.80 1.60 0.30 50% 5.80 3.00 4.35 1.30 75% 6.40 3.30 5.10 1.80 max 7.90 4.40 6.90 2.50Вызов метода describe для столбца 'species' подтверждает, что он содержит три уникальных значения. Нам заранее известно, что данные состоят из трех классов, к которым относятся образцы, хотя в машинном обучении без учителя это и не всегда так.
In [16]: iris_df['species'].describe() Out[16]: count 150 unique 3 top setosa freq 50 Name: species, dtype: object14.7.3. Визуализация набора данных функцией pairplot
Проведем визуализацию признаков в этом наборе данных. Один из способов извлечь информацию о ваших данных — посмотреть, как признаки связаны друг с другом. Набор данных имеет четыре признака. Мы не сможем построить диаграмму соответствия одного признака с тремя другими на одной диаграмме. Тем не менее можно построить диаграмму, на которой будет представлено соответствие между двумя признаками. Фрагмент [20] использует функцию pairplot библиотеки Seaborn для создания таблицы диаграмм, на которых каждый признак сопоставляется с одним из других признаков:
In [17]: import seaborn as sns In [18]: sns.set(font_scale=1.1) In [19]: sns.set_style('whitegrid') In [20]: grid = sns.pairplot(data=iris_df, vars=iris_df.columns[0:4], ...: hue='species') ...:Ключевые аргументы:
- коллекция DataFrame с набором данных, наносимым на диаграмму;
- vars — последовательность с именами переменных, наносимых на диаграмму. Для коллекции DataFrame она содержит имена столбцов. В данном случае используются первые четыре столбца DataFrame, представляющие длину (ширину) наружной доли околоцветника и длину (ширину) внутренней доли околоцветника соответственно;
- hue — столбец коллекции DataFrame, используемый для определения цветов данных, наносимых на диаграмму. В данном случае данные окрашиваются в зависимости от вида ирисов.
Предыдущий вызов pairplot строит следующую таблицу диаграмм 4 ? 4:
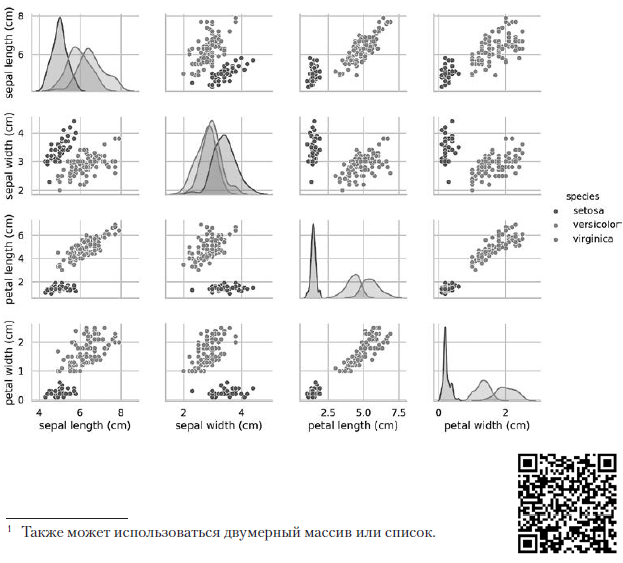
На других диаграммах в столбце представлены диаграммы разброса данных других признаков относительно признака по оси x. В первом столбце на первых трех диаграммах по оси y представлены ширина наружной доли околоцветника, длина внутренней доли околоцветника и ширина внутренней доли околоцветника соответственно, а на оси x — длина наружной доли околоцветника.
При выполнении этого кода на экране появляется цветное изображение, показывающее отношения между разными видами ирисов на уровне отдельных признаков. Интересно, что на всех диаграммах синие точки Iris setosa четко отделяются от оранжевых и зеленых точек других видов; это говорит о том, что Iris setosa действительно является отдельным классом. Также можно заметить, что других два вида иногда можно перепутать, на что указывают перекрывающиеся оранжевые и зеленые точки. Например, по диаграмме ширины и длины наружной доли околоцветника видно, что точки Iris versicolor и Iris virginica смешиваются. Это говорит о том, что если доступны только измерения наружной доли околоцветника, то различить эти два вида будет сложно.
Вывод результатов pairplot в одном цвете
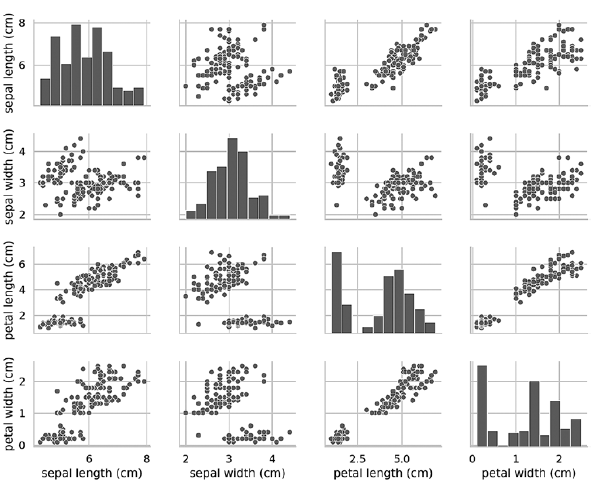
Если убрать ключевой аргумент hue, то функция pairplot использует только один цвет для вывода всех данных, потому что она не знает, как различать виды при выводе:
In [21]: grid = sns.pairplot(data=iris_df, vars=iris_df.columns[0:4])Как видно из следующей диаграммы, в данном случае диаграммы на диагонали представляют собой гистограммы с распределениями всех значений этого признака независимо от вида. При изучении диаграмм может показаться, что существуют всего два кластера, хотя мы знаем, что в наборе содержатся данные трех видов. Если количество кластеров неизвестно заранее, то можно обратиться к эксперту предметной области, хорошо знакомому с данными. Эксперт может знать, что в наборе данных присутствуют три вида; эта информация может пригодиться при проведении машинного обучения с данными.
» Более подробно с книгой можно ознакомиться и приобрести на сайте издательства