Исследование и преобразование сортировкой псевдослучайных последовательностей

Исследование и преобразование сортировкой псевдослучайных последовательностей

Созданы алгоритмы на языках C# и qbasic и таблица Excel совместимая, доказывающие возможность исследовать псевдослучайные последовательности на случайность и способные определять последовательности неслучайные или маломощные.

Графическая оболочка: таблица Excel совместимая для исследования свыше 50тыс. элементов 2-х видов:
1. Исследование последовательности чисел;
2. Исследование последовательности цифр 0 и 1.

Исследование последовательности чисел: таблица определяет двоичные признаки, например меньше/больше и чётность/нечётность. Графическая оболочка таблица Excel совместимая использует формулы:

Количество совпадений подряд рассчитывает формула N=log(1-C)/log(1-P), где N – шаг, P – вероятность, C – надёжность вероятности. Номер шага распределения:
при С=P=0,5; N = 1 = log0,5/log0,5 = log(1-1/2)/log(1-1/2) = 1
при C=0,25; P=0,5; N = 2 = log0,75/log0,5 = log(1-1/4)/log(1-1/2) = 2 и т.д.

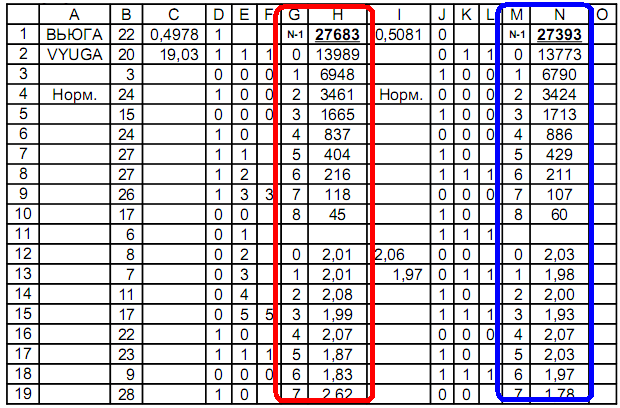
Столбец A – наименование последовательности;
Столбец B – последовательность;
Столбец D – 1-е распределение: меньше / больше;
Столбцы E, F – определение одинаковых подряд;
Столбцы G, H – подсчёт количества признаков одинаковых подряд;
Столбец J – 2-е распределение: чётные / нечётные;
Столбцы K, L – определение признаков одинаковых подряд;
Столбцы M, N – подсчёт количества признаков одинаковых подряд.

Формулы, используемые в таблице:

Яч.	Формула	Пояснение
С1	=СРЗНАЧ(D1:D55000)	Среднее значение чисел последовательности
C2	=СРЗНАЧ(B1:B55000)	Среднее значение распределения 1
D1	=ЕСЛИ(B1<C$2;0;1)	Если число меньше среднего, то 0, иначе 1
D2	=ЕСЛИ(B2<C$2;0;1)	Если число меньше ср., то 0, иначе 1 и т.д.
E2	=ЕСЛИ(D2=D1;E1+1;0)	Если одинаковые признаки распределения, то  счётчик одинаковых подряд +1, иначе счётчик обнуляется
F2	=ЕСЛИ(E3=0;E2;" ")	Если счётчик обнулён, фиксируется наибольший счётчик
G2-G19	0…7	Числа по порядку для сравнения
H1	=СУММ(H2:H10)	Сумма сравнений
H2	=СЧЁТЕСЛИ(F$1:F$55000;G2)	Количество признаков 1 подряд
H3	=СЧЁТЕСЛИ(F$1:F$55000;G3)	Количество признаков  2 подряд и т.д.
H12	=H2/H3	Отношение ближайших количеств признаков
I12	=СРЗНАЧ(H12:H19)	Среднее значение отношений
I13	=СРЗНАЧ(N12:N19)	Среднее значение отношений и т.д.
I1	=СРЗНАЧ(J1:J55000)	Среднее значение распределения 2
J1	=ЕСЛИ(B1/2=ЦЕЛОЕ(B1/2);0;1)	Если число чётное, то 0, иначе 1
J2	=ЕСЛИ(B2/2=ЦЕЛОЕ(B2/2);0;1)	Если число чётное, то 0, иначе 1 и т.д.
K2	=ЕСЛИ(J2=J1;K1+1;0)	Если одинаковые признаки распределения, то  счётчик одинаковых подряд +1, иначе счётчик обнуляется
L2	=ЕСЛИ(K3=0;K2;" ")	Если счётчик обнулён, фиксируется наибольший счётчик
M2-M19	0…7	Числа по порядку для сравнения
N1	=СУММ(N2:N10)	Сумма сравнений
N2	=СЧЁТЕСЛИ(L$1:L$55000;M2)	Количество признаков 1 подряд
N3	=СЧЁТЕСЛИ(L$1:L$55000;M3)	Количество признаков 2 подряд и т.д.
N12	=H2/H3	Отношение ближайших количеств признаков

В таблице возможно запрограммировать другие функции контроля.
В таблице возможно создавать графики значений любых ячеек.

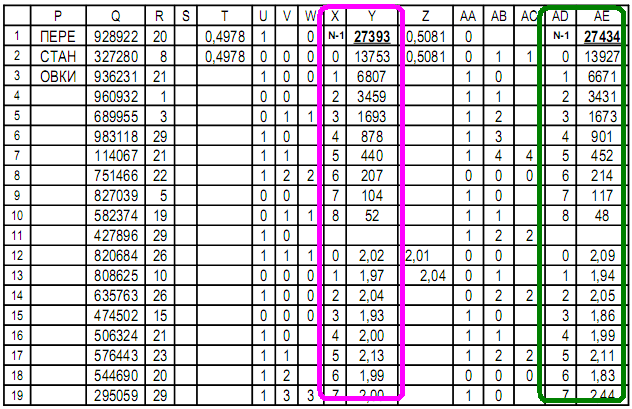
Продолжение таблицы исследует случайные перестановки последовательности

Столбец Q – случайные для перестановки: целые до 10^6, чтобы минимизировать повтор случайных; Столбец R – изначально копия столбца B и далее измененный; Столбцы T…AE – то же что столбцы C…N.

Яч.	Формула	Пояснение
Q1	=СЛУЧМЕЖДУ(0;1000000)	Случайное для перестановки
Q2	=СЛУЧМЕЖДУ(0;1000000)	Случайное для перестановки и т.д.

Перестановка осуществляется путём сортировки 2-х столбцов Q и R:
столбец Q ведущий и столбец R ведомый.

Результат: перестановки столбца R и новая последовательность.

Исследования ГПСЧ на основе встроенного ГПСЧ показывают нормальность алгоритма.
До перестановки 500 ячеек:

После перестановки 500 ячеек:

Проверка показывает распределение хорошее, сравнивая признаки: малые/большие и чётные/нечётные. Таблица исследует ГПСЧ тригонометрический, использующий цифры после запятой тригонометрических функций, стандартный ГПСЧ не используя.

'rndsin.bas OPEN "rndsin.txt" FOR OUTPUT AS #1 c = 0: a = SIN(TIMER) * 100 + 200 PRINT #1, "a= ", a  FOR k = 1 TO 10 ^ 3 + a * 10 ^ 3: NEXT  FOR i = 1 TO 100     FOR j = 1 TO a         x = SIN(TIMER) * 1000 + 2000         b = COS(x): c = c + b         LOCATE 1, 1: PRINT j     NEXT      d = (ABS(c)) - INT(ABS(c))     PRINT #1, d     FOR k = 1 TO 10000 + a * b * c * 10 ^ 2: NEXT NEXT

До перестановки 500 ячеек: неудовлетворительно

Очевидно распределение плохое, обнаруживая периодичность и разброс значений, сравнивая признаки: малые/большие и чётные/нечётные. После перестановки 500 ячеек: нормально

Цель: исключить встроенный ГПСЧ. Метод перестановки: исходная последовательность сортируется, в качестве случайных для перестановки принята та же последовательность, перевёрнутая или инвертированная любым способом.
Например, в Excel созданы 2 копии столбцов последовательности на расстоянии и у одного столбца слева выстроен ведущий ряд 1...55000 подряд и 2 столбца сортированы от максимального к минимальному, инвертировав исходные данные.

Далее 2 столбца последовательности сопоставлены рядом и сортированы, где столбец ведущий – обратный и столбец ведомый – начальный.

До перестановки 500 ячеек: неудовлетворительно

После перестановки 500 ячеек: нормально

Результат: последовательность стала нормальной без встроенного ГПСЧ. Выводы: истинная случайность для людей неестественна и возможно синтезировать последовательности маломощные или фальшивые, принимаемые людьми и компьютерами за случайные последовательности.
Любые последовательности реально синтезировать на языках программирования и в таблицах Excel совместимых.

Задача преодоления случайности решается распознаванием случайности нормальной или фальшивой в таблице Excel с графиками.

Что и требовалось доказать.