Генерирование псевдослучайных чисел с помощью клеточного автомата: Правило 30

Генераторы псевдослучайных чисел выдают числа детерминировано, но обычно такие числа выглядят непериодическими (случайными). По крайней мере, в большинстве случаев применения подобных чисел так обычно и происходит. Генератор принимает начальное значение (в идеале — истинное случайное число) и порождает последовательность чисел, работая как функция от начального значения и (или) от предыдущего числа последовательности. Подобные числа являются псевдослучайными (а не истинными случайными числами) из-за того, что если известно начальное значение, переданное генератору, эти числа можно сгенерировать снова алгоритмическим путём. Истинные случайные числа генерируют, используя специальное аппаратное обеспечение или некие физические явления — пульсовые колебания объёма крови, атмосферное давление, тепловой шум, квантовые процессы и так далее.

Существует множество способов генерирования псевдослучайных чисел. Например — алгоритм Блюма — Блюма — Шуба, метод средних квадратов, метод Фибоначчи с запаздываниями. Сегодня мы поговорим о генерировании случайных чисел с помощью Правила 30, которое использует неоднозначный подход, предусматривающий применение модели клеточного автомата. Этот метод прошёл множество стандартных тестов на случайность чисел и использовался в системе Mathematica для генерирования случайных целых чисел.

Клеточный автомат

Прежде чем мы перейдём к разговору о Правиле 30, уделим некоторое время клеточным автоматам. Клеточный автомат — это дискретная модель, состоящая из регулярной решётки ячеек любой размерности. Каждая из ячеек решётки может находиться в одном из конечного множества состояний. При этом для каждой ячейки определено такое понятие, как «окрестность». В окрестность некоей ячейки, например, могут входить все ячейки, находящиеся на расстоянии не более 2 от неё. Существуют правила, определяющие то, как ячейки взаимодействуют друг с другом и переходят в следующее поколение (состояние). Правила эти, в основном, представлены математическими (программируемыми) функциями, которые зависят от текущего состояния ячеек и от состояния их соседей.

Описание клеточного автомата

Описание клеточного автомата с предыдущего рисунка позволяет узнать о том, что каждая ячейка может находиться в одном из двух конечных состояний — 0 (показано красным) и 1 (показано чёрным). Каждая ячейка переходит в следующее поколение, принимая новое состояние, являющееся результатом применения операции XOR к её 8 соседям. Первое поколение (начальное состояние) решётки задаётся случайно. Ниже показана работа этого клеточного автомата.

Клеточный автомат, основанный на функции XOR, в действии

Идея клеточного автомата появилась в 1940-х годах благодаря Станиславу Уламу и Джону фон Нейману. Клеточные автоматы нашли применение в информатике, математике, физике, в теории сложных систем, в теоретической биологии, в задачах моделирования микроструктуры сред и материалов. В 1980-х Стивен Вольфрам провёл систематическое исследование одномерного клеточного автомата (его также называют элементарным клеточным автоматом), на котором и основано Правило 30.

Правило 30

Правило 30 — это элементарный (одномерный) клеточный автомат, в котором каждая ячейка может пребывать в одном из двух конечных состояния: 0 (красные ячейки на рисунке, приведённом ниже) и 1 (чёрные ячейки). Окрестности ячейки представлены её двумя ближайшими соседями, находящимися слева и справа от неё. Следующее состояние (поколение) ячейки зависит от её текущего состояния и от состояния её соседей. Правила перехода ячеек в следующее состояние показаны на следующем рисунке.

Правило 30

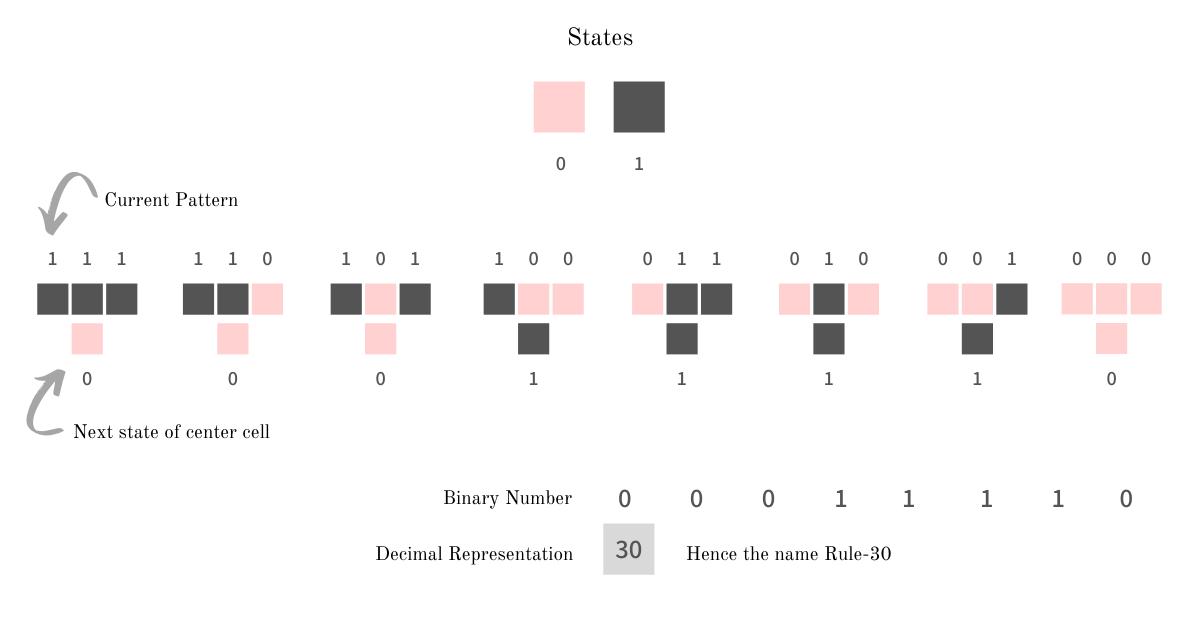
Эти правила перехода ячеек в новое состояние можно упрощённо записать так: left XOR (central OR right).

Мы выводим ячейки автомата в виде двумерной решётки, каждая строка которой представляет одно поколение (состояние). Когда вычисляется следующее поколение (состояние) ячеек, оно выводится ниже последнего известного состояния. Каждая строка содержит конечное количество ячеек, которые, в конце, «зацикливаются».

Правило 30 в действии

Вышеприведённый паттерн возникает из начального состояния (строка 0), когда одна ячейка имеет состояние 1 (чёрная), а все окружающие её ячейки имеют состояние 0 (красные). Состояние ячеек в следующем поколении (строка 1) вычисляется по вышеописанному правилу. Вертикаль решётки представляет собой время, а пересечения строк и столбцов представляют собой состояние конкретной ячейки на определённом этапе развития системы.

Поколение t и поколение t + 1

По мере развития паттерна в нём часто появляются красные треугольники разных размеров, но, в целом, в получающейся структуре нельзя распознать некий различимый паттерн. Вышеприведённый фрагмент решётки сделан в произвольно выбранный момент времени. Тут можно видеть хаос и апериодичность. Это свойство Правила 30 и используется для генерирования псевдослучайных чисел.

Генерирование псевдослучайных чисел

Как уже было сказано, Правило 30 демонстрирует апериодичное и хаотическое поведение. В результате его применение приводит к созданию сложных, и, как кажется, случайных паттернов по простым и чётко определённым правилам. Для генерирования случайных чисел с использованием Правила 30 используется центральный столбец решётки, из которого выбирается последовательность из n случайных битов, из которых формируется нужное n-битное случайное число. Следующее случайное число формируется с использованием следующих n битов из столбца.

Генерирование случайных чисел с использованием Правила 30

Если всегда начинать выбор ячеек с первой строки, то сгенерированная последовательность чисел всегда будет предсказуемой. А это — не то, что нам нужно. Для того чтобы создавать псевдослучайные числа, будем использовать случайное начальное значение (например — текущее время), пропускать соответствующее число строк, а уже после этого выбирать последовательности из n строк и создавать на их основе случайные числа.

Псевдослучайные числа, сгенерированные с использованием Правила 30, не являются криптографически безопасными, но они подходят для симуляций — до тех пор, пока мы не пользуемся неподходящими начальными значениями вроде 0.

Одно из серьёзных преимуществ применения Правила 30 для генерирования псевдослучайных чисел заключается в том, что можно создавать множество случайных чисел в параллельном режиме, случайным образом выбирая множество столбцов длины n бит. Вот пример псевдослучайной последовательности 8-битных чисел, сгенерированных этим методом с использованием начального значения 0: 220, 197, 147, 174, 117, 97, 149, 171, 240, 241.

Начальное значение, кроме того, может быть использовано для задания начального состояния модели (строки №0). В результате псевдослучайные числа можно получать, просто выбирая по n бит из центрального столбца, начиная с нулевой строки. Этот подход эффективнее, но он сильно зависит от качества начального значения. Неудачно выбранное начальное значение может привести к появлению хорошо предсказуемых чисел. Демонстрацию этого подхода можно найти здесь.

Правило 30 в реальном мире

Правило 30 можно видеть в природе, в форме узора на раковине брюхоногого моллюска вида Conus textile. Железнодорожная станция Кембридж-Северный оформлена панелями, изображающими результаты эволюции модели, построенной с использованием Правила 30.

Итоги

Если вы нашли Правило 30 интересным — рекомендую написать собственную симуляцию с использованием библиотеки p5. Реализовать этот алгоритм можно в достаточно общем виде, что позволит одной и той же программе генерировать паттерны для разных правил — 90, 110, 117 и так далее. Паттерны, сгенерированные с использованием различных правил, весьма интересны. Если хотите, можете перейти на следующий уровень. Можете расширить модель до трёх измерений и исследовать эволюцию паттернов. Я думаю, что программирование способно принести массу удовольствия в том случае, если в нём есть визуальная составляющая. Восхитительно, когда две, как кажется, несвязанные друг с другом области науки, клеточные автоматы и криптография, объединяются ради создания чего-то удивительного. Хотя описанный здесь алгоритм больше не применяется достаточно широко из-за появления более эффективных алгоритмов, он подталкивает нас к креативному использованию клеточных автоматов.