предыдущие главы
30 Интерпретация кривой обучения: Большое смещение
Предположим, ваша кривая ошибок на валидационной выборке выглядит следующим образом:
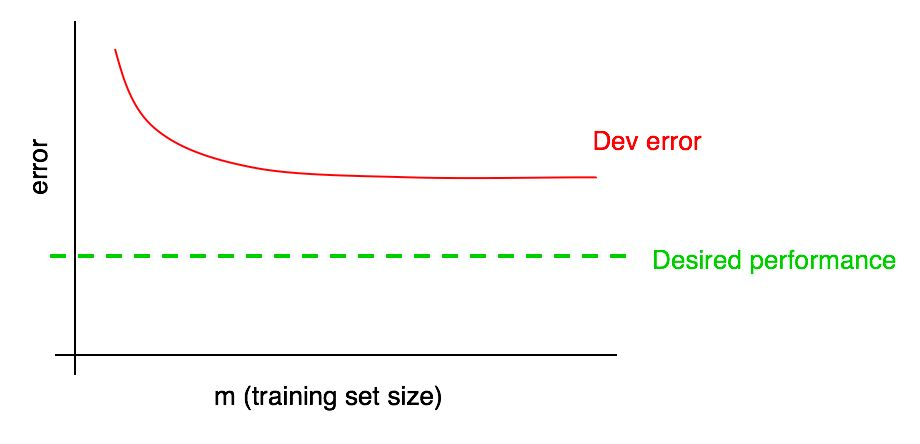
Мы уже говорили, что если ошибка алгоритма на валидационной выборке вышла на плато, вы вряд ли сможете достигнуть желаемого уровня качества просто добавляя данные.
Но трудно предположить, как будет выглядеть экстраполяция кривой зависимости качества алгоритма на валидационной выборке (Dev error) при добавлении данных. А если валидационная выборка маленькая, то ответить на этот вопрос еще сложнее из-за того, что кривая может быть зашумлена (иметь большой разброс точек).
Предположим, мы добавили на наш график кривую зависимости величины ошибки от количества данных тестовой выборки и получили следующую картину:
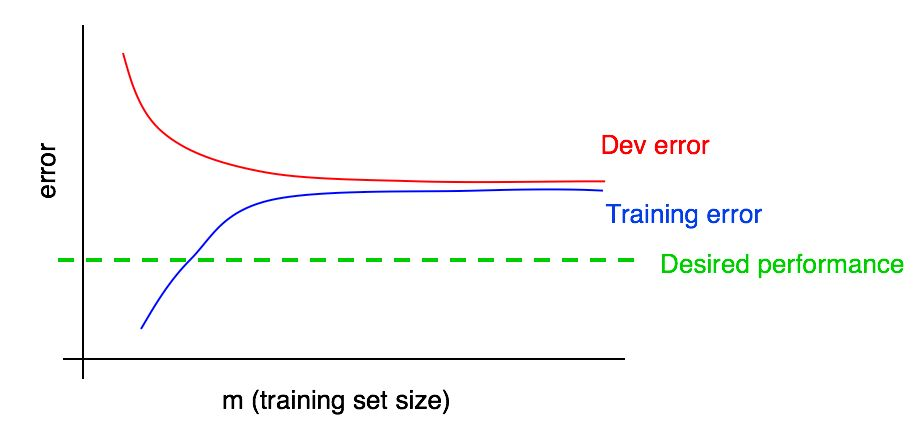
Посмотрев на эти две кривые можно быть абсолютно уверенными, что добавление новых данных само по себе не даст желаемого эффекта (не позволит увеличить качество работы алгоритма). Откуда можно сделать такой вывод?
Давайте вспомним следующие два замечания:
- Если мы добавляем больше данных в тренировочную выборку, ошибка алгоритма на тренировочной выборке может только увеличиться. Таким образом, синия линия нашего графика либо не изменится, либо поползет вверх и будет удаляться от желаемого уровня качества нашего алгоритма (зеленая линия).
- Красная линия ошибки на валидационной выборке обычно выше, чем синия линия ошибки алгоритма на тренировочной выборке. Таким образом, здесь ни при каких мыслимых обстоятельствах, добавлении данных не приведет к дальнейшему понижению красной линии, не сблизит ее с желаемым уровнем ошибки. Это практически невозможно, если учесть, что даже ошибка на тренировочной выборке выше желаемой.
Рассмотрение обеих кривых зависимостей ошибки алгоритма от количества данных в валидационной и в тренировочной выборках на одном графике, позволяет более уверенно экстраполировать кривую ошибки обучающегося алгоритма от количества данных в валидационной выборке.
Допустим, что у нас есть оценка желаемого качества работы алгоритма в виде оптимального уровня ошибок работы нашей системы. В этом случае приведенные выше графики являются иллюстрацией стандартного «хрестоматийного» случая как выглядит кривая обучения с высоким уровнем устранимого смещения. На наибольшем размере тренировочной выборки, предположительно, соответствующему всем данным, которые есть в нашем распоряжении, наблюдается большой разрыв между ошибкой алгоритма на тренировочной выборке и желаемым качеством работы алгоритма, что указывает на высокий уровень избегаемого смещения. Кроме того, разрыв между ошибкой на тренировочной выборке и ошибкой на валидационной выборке маленький, что свидетельствует о небольшом разбросе.
Ранее мы обсуждали ошибки алгоритмов, обученных на тренировочной и валидационной выборках только в самой правой точке выше приведенного графика, которая соответствует использованию всех имеющихся у нас тренировочных данных. Кривая зависимостей ошибки от количества данных тренировочной выборки, построенная для разных размеров выборки, используемой для обучения, дает нам более полное представление о качестве работы алгоритма, обученного на различных размерах тренировочной выборки.
31 Интерпретация кривой обучения: остальные случаи
Рассмотрим кривую обучения:
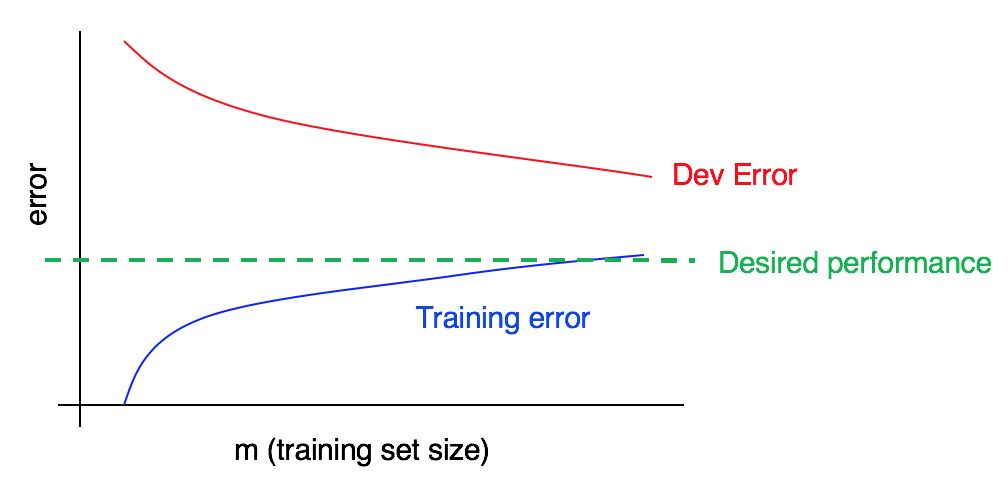
На этом графике зафиксировано высокое смещение, высокий разборос или оба сразу?
Синяя кривая ошибки на тренировочных данных относительно низкая, красная кривая ошибки на валидационных данных значительно выше синей ошибки на тренировочных данных. Таким образом, в данном случае смещение маленькое, но разброс большой. Добавление большего количества тренировочных данных, возможно, поможет закрыть разрыв между ошибкой на валидационной выборке и ошибкой на тренировочной выборке.
А теперь рассмотрим вот этот график:
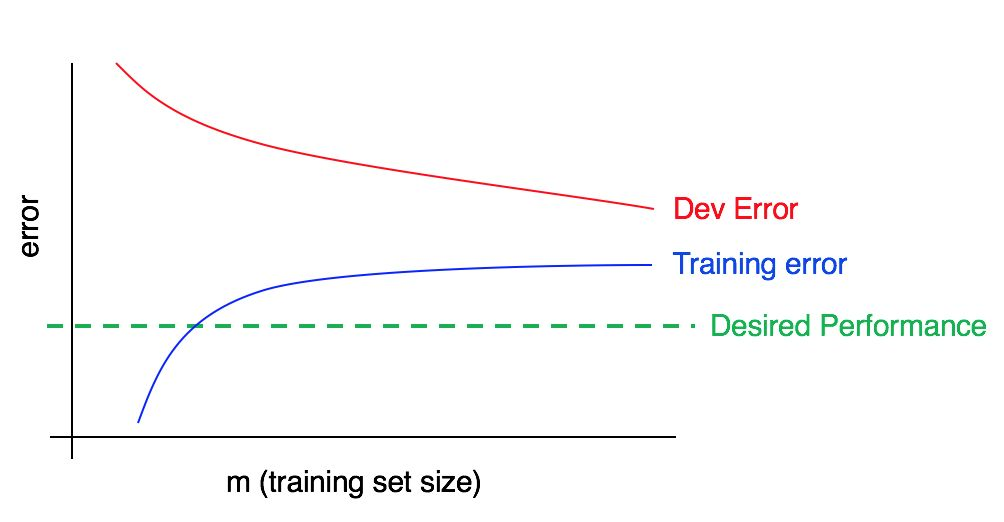
В этом случае ошибка на тренировочной выборке большая, она существенно выше соответствующей желаемому уровню качества работы алгоритма. Ошибка на валидационной выборке так же существенно выше ошибки на тренировочной выборке. Таким образом имеем дело с одновременно большими смещением и разбросом. Вы должны искать пути уменьшения и смещения и разброса в работе вашего алгоритма.
продолжение следует