Основы deep learning на примере дебага автоэнкодера, часть №1

Если почитать обучение по автоэнкодерам на сайте keras.io, то один из первых посылов там звучит примерно так: на практике автоэнкодеры почти никогда не используются, но про них часто рассказывают в обучалках и народу заходит, поэтому мы решили написать свою обучалку про них:

Their main claim to fame comes from being featured in many introductory machine learning classes available online. As a result, a lot of newcomers to the field absolutely love autoencoders and can't get enough of them. This is the reason why this tutorial exists!

Тем не менее, одна из практических задач, для которых их вполне себе можно применять — поиск аномалий, и лично мне в рамках вечернего проекта потребовался именно он.

На просторах интернетов есть очень много туториалов по автоэнкодерам, нафига писать еще один? Ну, если честно, тому было несколько причин:

• Сложилось ощущение, что на самом деле туториалов примерно 3 или 4, все остальные их переписывали своими словами;
• Практически все — на многострадальном MNIST'е с картинками 28х28;
• На мой скромный взгляд — они не вырабатывают интуицию о том, как это все должно работать, а просто предлагают повторить;
• И самый главный фактор — лично у меня при замене MNIST'а на свой датасет — оно все тупо переставало работать.

Дальше описан мой путь, на котором набиваются шишки. Если взять любую из предложенных плоских (не сверточных) моделей из массы туториалов и втупую ее скопипастить — то ничего, как это ни удивительно, не работает. Цель статьи — разобраться почему и, как мне кажется, получить какое-то интуитивное понимание о том, как это все работает.

Я не специалист по машинному обучению и использую подходы, к которым привык в повседневной работе. Для опытных data scientists наверное вся эта статья будет дикой, а для начинающих, как мне кажется, может что-то новое и встретится.

Начнем. У меня есть датасет из 4000 черно-белых картинок 64х64 пикселя, выглядит он примерно вот так:

Просто какие-то линии на черном фоне, причем на картинке 64х64 заполнено порядка 2% точек. Если посмотреть много картинок, то там, конечно, оказывается, что большая часть линий довольно похожа.

Не буду углубляться в подробности того, как датасет загружался, обрабатывался, ибо цель статьи, опять таки, не это. Просто покажу страшный кусок кода.

Код

# only for google colab %tensorflow_version 2.x  import tensorflow as tf import numpy as np import matplotlib.pyplot as plt import os import zipfile import datetime import tensorflow_addons as tfa  BATCH_SIZE = 128 AUTOTUNE=tf.data.experimental.AUTOTUNE  def load_image(fpath):   img_raw = tf.io.read_file(fpath)   img = tf.io.decode_png(img_raw, channels=1, dtype=tf.uint8)   return tf.image.convert_image_dtype(img, dtype=tf.float32)  ## for splitting test/train def is_test(x, y):   return x % 4 == 0  def is_train(x, y):   return not is_test(x,y)  ## for image augmentation def random_flip_flop(img):   return tf.image.random_flip_left_right(img)  def transform_aug(shift_val):   def random_transform(img):     return tfa.image.translate(img,tf.random.uniform([2], -1*shift_val, shift_val))   return random_transform  def prepare_for_training(ds, cache=True, shuffle_buffer_size=1000, transform=0, flip=False):   if cache:     if isinstance(cache, str):       ds = ds.cache(cache)     else:       ds = ds.cache()    ds = ds.shuffle(buffer_size=shuffle_buffer_size)    if transform != 0:     ds = ds.map(transform_aug(transform))    if flip:     ds = ds.map(random_flip_flop)    ds = ds.repeat()   ds = ds.batch(BATCH_SIZE)   ds = ds.prefetch(buffer_size=AUTOTUNE)    return ds  def prepare_input_output(x):     return (x, x)  list_ds = tf.data.Dataset.list_files("/content/planes64/*") imgs_df = list_ds.map(load_image)  train = imgs_df.enumerate().filter(is_train).map(lambda x,y: y) train_ds = prepare_for_training(train, transform=10, flip=True) train_ds = train_ds.map(prepare_input_output)  val = imgs_df.enumerate().filter(is_test).map(lambda x, y: y) val_ds = val.map(prepare_input_output).batch(BATCH_SIZE, drop_remainder=True)

Вот, например, первая же предложенная модель с keras.io, которая у них на mnist'е работала и обучалась:

# this is the size of our encoded representations encoding_dim = 32  # 32 floats -> compression of factor 24.5, assuming the input is 784 floats  # this is our input placeholder input_img = Input(shape=(784,)) # "encoded" is the encoded representation of the input encoded = Dense(encoding_dim, activation='relu')(input_img) # "decoded" is the lossy reconstruction of the input decoded = Dense(784, activation='sigmoid')(encoded)

В моем случае модель определена вот так:

model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64/10, activation='relu'))  model.add(tf.keras.layers.Dense(64*64, activation="sigmoid")) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))

Есть небольшие отличия, что я прямо в модели делаю flatten и reshape, и что "сжимаю" не в 25 раз, а всего в 10. Ни на что влиять это не должно.

В качестве loss-функции — mean squared error, оптимизатор не принципиален, пусть adam. Здесь и далее, тренируем 20 эпох, по 100 шагов в эпохе.

Если посмотреть на метрики — все в огне. Accuracy == 0.993. Если посмотреть на графики обучения — все чуть грустнее, выходим на плато в районе третьей эпохи.

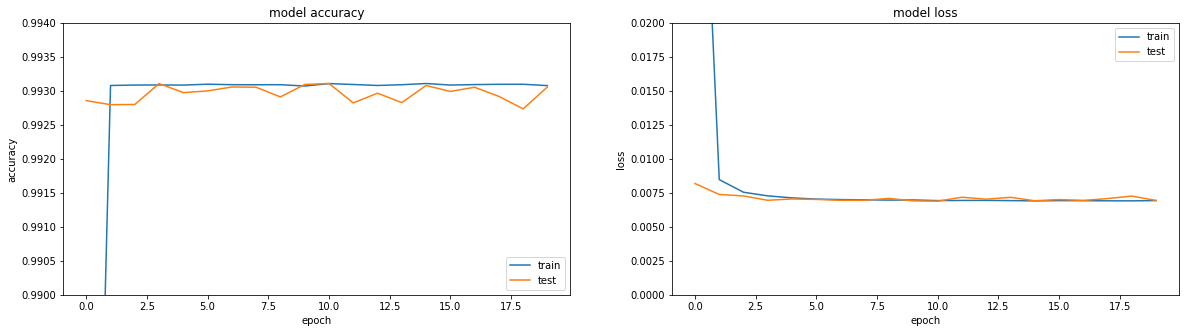
Ну и если посмотреть непосредственно на результат работы энкодера, то выходит вообще грустная картина (сверху оригинал, снизу — результат кодирования-декодирования):

В целом, когда пытаешься разобраться почему что-то не работает — достаточно хорошим подходом бывает разбить весь функционал на большие блоки и проверить каждый из них в изоляции. Так и поступим.

В оригинале туториала — на вход модели подается плоские данные и на выходе берутся они же. Почему бы не проверить мои действия по flatten и reshape. Вот такая no-op модель:

model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))

Результат:

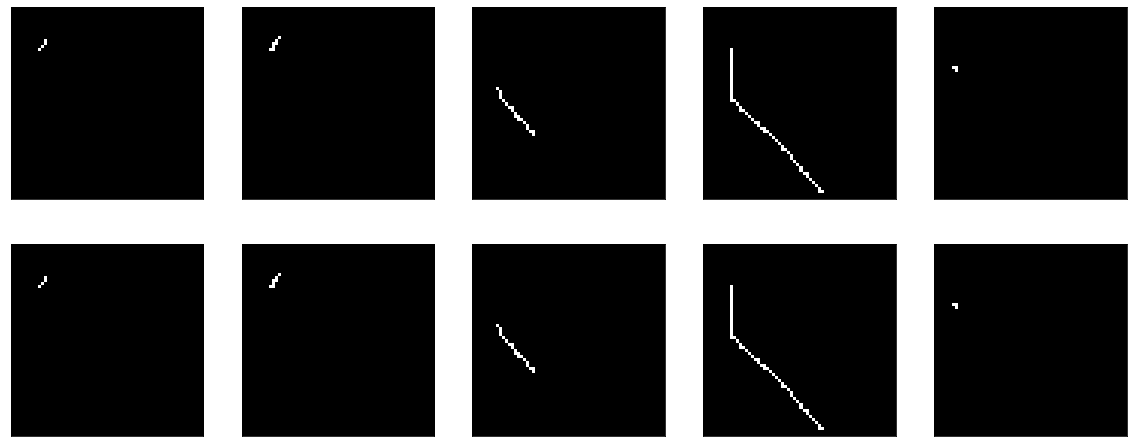
Обучать тут ничего не надо. Ну и заодно оно доказало, что моя функция визуализации тоже работает.

Дальше попробуем, чтобы модель была не no-op, но максимально тупой — просто вырезаем слой сжатия, оставляем один слой размером с input. Как пишут во всех туториалах, мол, очень важно, чтобы ваша модель учила фичи, а не была просто identity функцией. Ну а мы именно это и попробуем получить, пусть себе просто передает полученную картинку на выход.

model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation="sigmoid")) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))

Чему-то она учится, accuracy == 0.995 и опять утыкается в плато.

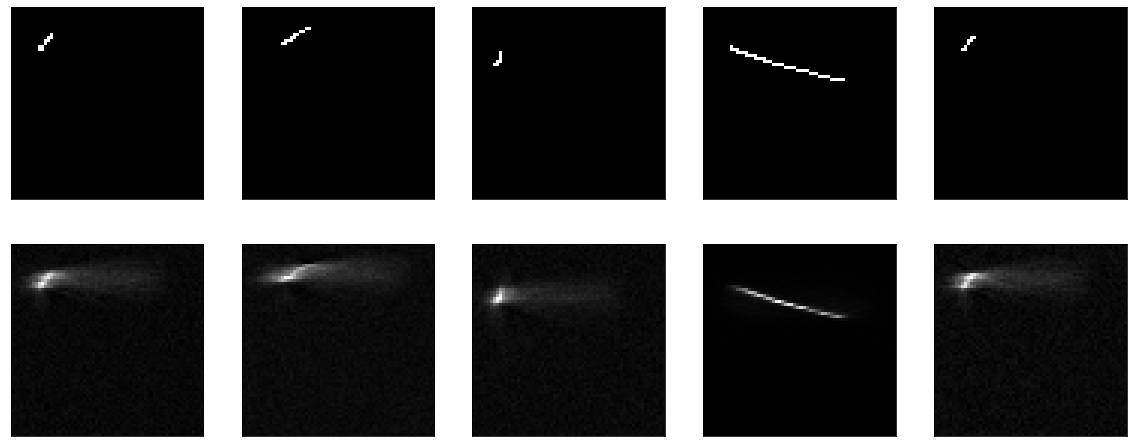
Но, в целом, видно, что получается не очень хорошо. Да и вообще — чему там учиться, передавай вход на выход и все.

Если почитать документацию keras'а про dense слои, то там описывается, что они делают: output = activation(dot(input, kernel) + bias)
Чтобы output совпал с input'ом достаточно двух простых вещей — bias = 0 и kernel — единичная матрица (тут важно не пустать с матрицой, заполненой единицами — это сильно разные штуки). Благо, и то и то можно сделать достаточно легко из документации к той же Dense.

model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation = "sigmoid", use_bias=False, kernel_initializer = tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))

Т.к. веса мы задали сразу, то можно ничего не учить — сразу выходит хорошо:

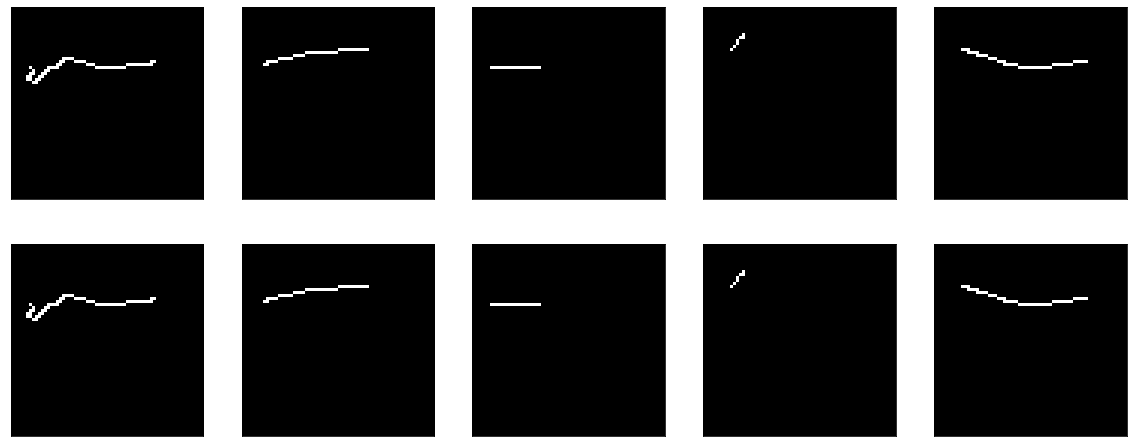
Но вот если запустить обучение — то тут начинается, на первый взгляд, удивительное — модель начинает с accuracy == 1.0, но он быстро падает.
Результат evaluate до обучения: 8/Unknown - 1s 140ms/step - loss: 0.2488 - accuracy: 1.0000[0.24875330179929733, 1.0]. Обучение:

Epoch 1/20 100/100 [==============================] - 6s 56ms/step - loss: 0.1589 - accuracy: 0.9990 - val_loss: 0.0944 - val_accuracy: 0.9967 Epoch 2/20 100/100 [==============================] - 5s 51ms/step - loss: 0.0836 - accuracy: 0.9964 - val_loss: 0.0624 - val_accuracy: 0.9958 Epoch 3/20 100/100 [==============================] - 5s 50ms/step - loss: 0.0633 - accuracy: 0.9961 - val_loss: 0.0470 - val_accuracy: 0.9958 Epoch 4/20 100/100 [==============================] - 5s 48ms/step - loss: 0.0520 - accuracy: 0.9961 - val_loss: 0.0423 - val_accuracy: 0.9961 Epoch 5/20 100/100 [==============================] - 5s 48ms/step - loss: 0.0457 - accuracy: 0.9962 - val_loss: 0.0357 - val_accuracy: 0.9962

Да и не очень понятно, у нас уже идеальная модель — картинка выходит 1 в 1, а loss (mean squared error) — показывает 0.25 почти.

Это, кстати, частый вопрос на форумах — loss падает, а accuracy не растет, как такое может быть?
Тут стоит вспомнить еще раз определение слоя Dense: output = activation(dot(input, kernel) + bias) и упомянутое в нем слово activation, которое я так успешно проигнорировал выше. С весами из identity матрицы и без bias мы получаем output = activation(input).

Собственно, функция активации у нас в исходнике-то уже указана, sigmoid, я ее довольно тупо копипастил и все. Да и в туториалах ее везде советуют использовать. Но придется разобраться.

Для начала, можно почитать в документации, что про нее пишут: The sigmoid activation: (1.0 / (1.0 + exp(-x))). Что лично мне не говорит ничего, ибо я не фантомас ни разу, чтобы такие графики в голове строить.
Но можно построить ручками:

import matplotlib.ticker as plticker range_tensor = tf.range(-4, 4, 0.01, dtype=tf.float32) fig, ax = plt.subplots(1,1) plt.plot(range_tensor.numpy(), tf.keras.activations.sigmoid(range_tensor).numpy()) ax.grid(which='major', linestyle='-', linewidth='0.5', color='red') ax.grid(which='minor', linestyle=':', linewidth='0.5', color='black') ax.yaxis.set_major_locator(plticker.MultipleLocator(base=0.5) ) plt.minorticks_on()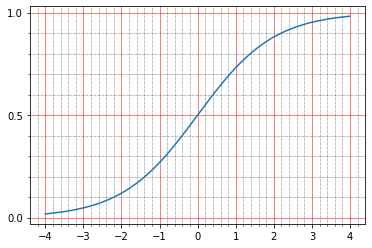

И вот тут становится видно, что в нуле сигмойд принимает значение 0.5, а в единице — в районе 0.73. А точки у нас бывают или черными (0.0), или белыми (1.0). Вот и выходит, что mean squared error у identity функции остается не нулевым.

Можно даже посмотреть ручками, вот одна строка из результирующей картинки:

array([0.5      , 0.5      , 0.5      , 0.5      , 0.5      , 0.5      ,        0.5      , 0.5      , 0.5      , 0.5      , 0.7310586, 0.7310586,        0.5      , 0.5      , 0.5      , 0.5      , 0.5      , 0.5      ,        0.5      , 0.5      , 0.5      , 0.5      , 0.5      , 0.5      ,        0.5      , 0.5      , 0.5      , 0.5      , 0.5      , 0.5      ,        0.5      , 0.5      , 0.5      , 0.5      , 0.5      , 0.5      ,        0.5      , 0.5      , 0.5      , 0.5      , 0.5      , 0.5      ,        0.5      , 0.5      , 0.5      , 0.5      , 0.5      , 0.5      ,        0.5      , 0.5      , 0.5      , 0.5      , 0.5      , 0.5      ,        0.5      , 0.5      , 0.5      , 0.5      , 0.5      , 0.5      ,        0.5      , 0.5      , 0.5      , 0.5      ], dtype=float32)

И это все, на самом деле, очень круто, ибо появляется сразу несколько вопросов:

• почему этого не было видно на визуализации выше?
• а почему тогда accuracy == 1.0, ведь исходные картинки ж 0 и 1.

С визуализацией — все удивительно просто. Для отображения картинок, я использовал matplotlib: plt.imshow(res_imgs[i][:, :, 0]). И, как обычно, если пойти в документацию, то все там будет написано: The Normalize instance used to scale scalar data to the [0, 1] range before mapping to colors using cmap. By default, a linear scaling mapping the lowest value to 0 and the highest to 1 is used. Т.е. библиотека заботливо нормализовала мои 0.5 и 0.73 в диапазон от 0 до 1. Меняем код:

plt.imshow(res_imgs[i][:, :, 0], norm=matplotlib.colors.Normalize(0.0, 1.0))

А вот дальше вопрос с accuracy. Для начала — по привычке идем в документацию, читаем за tf.keras.metrics.Accuracy и там вроде пишут понятное:

For example, if y_true is [1, 2, 3, 4] and y_pred is [0, 2, 3, 4] then the accuracy is 3/4 or .75.

Но в этом случае у нас accuracy должна была быть 0. Я, в результате, закопался в исходники и там вполне себе понятно написано:

 When you pass the strings 'accuracy' or 'acc', we convert this to one of `tf.keras.metrics.BinaryAccuracy`, `tf.keras.metrics.CategoricalAccuracy`, `tf.keras.metrics.SparseCategoricalAccuracy` based on the loss function used and the model output shape. We do a similar conversion for the strings 'crossentropy' and 'ce' as well.

Причем в документации на сайте почему-то этого параграфа нет в описании .compile.

Приведу кусок кода из https://github.com/tensorflow/tensorflow/blob/66c48046f169f3565d12e5fea263f6d731f9bfd2/tensorflow/python/keras/engine/compile_utils.py

y_t_rank = len(y_t.shape.as_list()) y_p_rank = len(y_p.shape.as_list()) y_t_last_dim = y_t.shape.as_list()[-1] y_p_last_dim = y_p.shape.as_list()[-1]  is_binary = y_p_last_dim == 1 is_sparse_categorical = (     y_t_rank < y_p_rank or y_t_last_dim == 1 and y_p_last_dim > 1)  if metric in ['accuracy', 'acc']: if is_binary:     metric_obj = metrics_mod.binary_accuracy elif is_sparse_categorical:     metric_obj = metrics_mod.sparse_categorical_accuracy else:     metric_obj = metrics_mod.categorical_accuracy

y_t это y_true, или ожидаемый результат на выходе, y_p это y_predicted, или результат по предсказанию.
Формат данных у нас: shape=(64,64,1), вот и выходит, что accuracy считается как binary_accuracy. Интереса ради, как он считается:

def binary_accuracy(y_true, y_pred, threshold=0.5):   threshold = math_ops.cast(threshold, y_pred.dtype)   y_pred = math_ops.cast(y_pred > threshold, y_pred.dtype)   return K.mean(math_ops.equal(y_true, y_pred), axis=-1)

Забавно, что здесь нам просто повезло — по умолчанию единицей считается все, что больше 0.5, а 0.5 и меньше — нулем. Вот и выходит accuracy стопроцентная для нашей identity модели, хотя на самом деле числа там совсем не такие же. Ну и, понятно, что если нам очень захочется — то можно поправить threshold и свести accuracy к нулю, например, только оно не особо нужно. Это ж метрика, на обучение не влияет, просто нужно понимать, что посчитать ее можно тыщей разных путей и получить абсолютно разные показатели. Просто как пример, можно ручками подергать разные метрики и по-передавать в них наши данные:

m = tf.keras.metrics.BinaryAccuracy() m.update_state(x_batch, res_imgs) print(m.result().numpy())

Даст нам 1.0.

А вот

m = tf.keras.metrics.Accuracy() m.update_state(x_batch, res_imgs) print(m.result().numpy())

Даст нам 0.0 на тех же самых данных.

Кстати, тот же самый кусок кода можно использовать, чтобы поиграть с loss-функциями и понять как они работает. Если почитать туториалы по автоэнкодерам, то в основном предлагают использовать одну из двух loss-функций: либо mean squared error, либо 'binary_crossentropy'. Можно заодно на них и посмотреть.

Напоминаю, для mse я уже давал evaluate модели:

8/Unknown - 2s 221ms/step - loss: 0.2488 - accuracy: 1.0000[0.24876083992421627, 1.0]

Т.е. loss == 0.2488. Давайте разберемся почему такой. Мне лично кажется, что он самый простой и понятный: по-пиксельно вычитается разница между y_true и y_predict, каждый результат возвоздится в квадрат, а потом ищется среднее.

tf.keras.backend.mean(tf.math.squared_difference(x_batch[0], res_imgs[0]))

И на выходе:

<tf.Tensor: shape=(), dtype=float32, numpy=0.24826494>

Тут интуиция очень простая — пустых пикселей большинство, модель в них выдает 0.5, получается 0.25 — squared difference для них.

C binary crossenttrtopy все чуть сложнее, и есть целые статьи о том, как это работает, но лично мне всегда было проще почитать исходники, и там это выглядит примерно вот так:

  if from_logits:     return nn.sigmoid_cross_entropy_with_logits(labels=target, logits=output)    if not isinstance(output, (ops.EagerTensor, variables_module.Variable)):     output = _backtrack_identity(output)       if output.op.type == 'Sigmoid':         # When sigmoid activation function is used for output operation, we         # use logits from the sigmoid function directly to compute loss in order         # to prevent collapsing zero when training.         assert len(output.op.inputs) == 1         output = output.op.inputs[0]         return nn.sigmoid_cross_entropy_with_logits(labels=target, logits=output)    # Compute cross entropy from probabilities.   bce = target * math_ops.log(output + epsilon())   bce += (1 - target) * math_ops.log(1 - output + epsilon())   return -bce

Если честно, я очень долго ломал голову над этими несколькими строчками кода. Во-первых, сразу видно, что может сработать две имплементации: либо будет вызван sigmoid_cross_entropy_with_logits, либо сработает последняя пара строчек. Разница в том, что sigmoid_cross_entropy_with_logits работает с логитами(как видно из названия, doh), а основной код — с вероятностями.

Кто такое логиты? Если почитать миллион разных статей на тему, то там будут упоминать математические определения, формулы, еще что-то. На практике, судя по всему, все удивительно просто(поправьте меня, если я не прав). Сырой выход предсказания — это логиты. Ну или log-odds, логарифмические шансы, которые измеряются в logistic units — логистических попугаях.

ln(1/2) == -0.69 ln(2/1) == 0.69 ln(1/100) == -4.6 ln(100/1) == 4.6

В случае с tensorflow — это достаточно условно, т.к., строго говоря, выход слоя математически не является log-odds, но так уж принято. Если сырое значение от -? до +? — то логиты. Дальше их можно преобразовать в вероятности. Для этого есть два варианта: softmax и его частный случай — sigmoid. Softmax — Возьмет вектор логитов, и преобразует их в вектор вероятностей, да еще и так, что сумма вероятности всех событий в нем окажется равна 1. Sigmoid(в случае tf) тоже возьмет вектор логитов, но преобразует каждый из них в вероятности отдельно, независимо от остальных.

# 1+ln(0.5) == 0.30685281944  tf.math.softmax(tf.constant([0.30685281944, 1.0, 0.30685281944])) ## <tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.25, 0.5 , 0.25], dtype=float32)> tf.math.sigmoid(tf.constant([0.30685281944, 1.0, 0.30685281944])) ## <tf.Tensor: shape=(3,), dtype=float32, numpy=array([0.57611686, 0.7310586 , 0.57611686], dtype=float32)>

Можно на это посмотреть с такой стороны. Есть задачи multi-label classification, есть задачи multi-class classification. Multiclass — это если вам надо определить, яблоки на картинке или апельсины, а может и вовсе ананасы. А multilabel — это когда на картинке может быть фруктовая ваза и вам надо сказать, что на ней есть и яблоки и апельсины, а ананасов нет. Если хотим multiclass — нужен softmax, если хотем multilabel — нужен sigmoid.
Вот у нас случай multilabel — надо для каждого отдельного пикселя(класса) сказать, установлен ли он.

Возвращаясь к tensorflow и почему в binary crossentropy (на самом далее в остальных crossentropy функциях примерно так же) — две глобальных ветки. Crossentropy всегда работает с вероятностями, об этом мы еще поговорим чуть ниже. Дальше просто два пути: либо на вход уже попадают вероятности, либо на вход приходят логиты — и тогда к ним сначала применяется sigmoid, чтобы получить вероятность. Так получилось, что применить sigmoid и посчитать crossentropy оказалось лучше, чем просто посчитать crossentropy из вероятностей (математический вывод причин есть в исходниках функции sigmoid_cross_entropy_with_logits, плюс для любопытных можно погуглить 'numerical stability cross entropy'), поэтому даже разработчики tensorflow рекомендуют не передавать вероятность на входе crossentropy функций, а отдавать туда сырые логиты. Ну и прямо в коде loss-функции проверяют, если последний слой — sigmoid, то они его отрежут и возьмут для расчета вход активации, а не ее выход, отправив все считаться в sigmoid_cross_entropy_with_logits.

Ладно, с этим разобрались, теперь binary_crossentropy. Есть два популярных "интуитивных" объяснения, что меряет cross-entropy.

Более формальное: представим, что есть некая модель, которая для n классов знает вероятность их возникновения(y₀, y₁, ..., y_n). А теперь в жизни у нас каждый из этих классов возник k_n раз(k₁, k₁, ..., k_n). Вероятность такого события — это произведение вероятности для каждого отдельного класса — (y₁^k₁)(y₂^k₂)...(y_n^k_n). В принципе — это уже нормальное определение кросс-энтропии — вероятность одного датасета выраженная в терминах вероятности другого датасета. Проблема такого определения в том, что оно окажется от 0 до 1 и часто будет очень маленьким, сравнивать такие значения не удобно.
Если взять от этого логарифм — выйдет k₁log(y₁) + k₂log(y₂) ну и так далее. Диапазон значений становится от -? до 0. Умножим все это на -1/n — и выходит диапазон от 0 до +?, мало того, т.к. оно выражается как сумма значений для каждого класса, то изменение каждого класса отражается на общем значении очень предсказуемым образом.

Более простое: кросс-энтропия показывает, сколько нужно дополнительно бит, чтобы выразить выборку в терминах изначальной модели. Если бы мы там делали логарифм с основанием 2 — то вышли бы прямо биты. Мы используем везде натуральные логарифмы, поэтому они показывают количество nat'ов (https://en.wikipedia.org/wiki/Nat_(unit)), а не битов.

Binary cross-entropy, в свою очередь, это частный случай обычной кросс-энтропии, когда количество классов равно двум. Тогда нам хватает знания вероятности возникновения одного класса — y₁, а вероятность возникновения второго будет (1-y₁).

Но, как мне кажется, меня чуток занесло. Напомню, в прошлый раз мы пытались построить identity автоэнкодер, картинку он нам показывал красивую, и даже accuracy в 1.0, но по факту циферки оказывались какие попало. Ради эксперимента, можно провести еще парочку тестов:
1) можно убрать вообще активацию, будет чистый identity
2) можно попробовать другие функции активации, например тот же relu

Без активации:

model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, use_bias=False, kernel_initializer=tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))

Получаем идеальную identity модель:

model.evaluate(x=val.map(lambda x: (x,x)).batch(BATCH_SIZE, drop_remainder=True)) #  8/Unknown - 1s 173ms/step - loss: 0.0000e+00 - accuracy: 1.0000[0.0, 1.0]

Обучение, кстати, ни к чему не приведет, ибо loss == 0.0.

Теперь с relu. Его график выглядит вот так:

import matplotlib.ticker as plticker range_tensor = tf.range(-4, 4, 0.01, dtype=tf.float32) fig, ax = plt.subplots(1,1) plt.plot(range_tensor.numpy(), tf.keras.activations.relu(range_tensor).numpy()) ax.grid(which='major', linestyle='-', linewidth='0.5', color='red') ax.grid(which='minor', linestyle=':', linewidth='0.5', color='black') ax.yaxis.set_major_locator(plticker.MultipleLocator(base=1) ) plt.minorticks_on()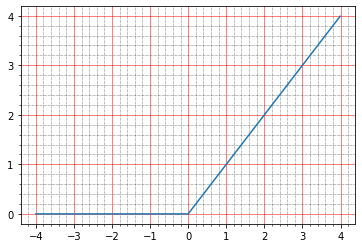

Ниже нуля — ноль, выше — y=x, т.е. в теории мы должны получить тот же эффект, что и при отсутствии активации — идеальную модель.

model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='relu', use_bias=False, kernel_initializer=tf.keras.initializers.Identity())) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))  model.compile(optimizer="adam", loss="binary_crossentropy", metrics=["accuracy"])  model.evaluate(x=val.map(lambda x: (x,x)).batch(BATCH_SIZE, drop_remainder=True)) #    8/Unknown - 1s 158ms/step - loss: 0.0000e+00 - accuracy: 1.0000[0.0, 1.0]

Ладно, с identity моделью разобрались, даже с какой-то частью теории стало понятнее. Теперь попробуем ту же модель обучить, чтобы она стала identity.

Смеха ради, проведу этот эксперимент на трех функциях активации. Для начала — relu, ибо он показал себя хорошо раньше(все как раньше, но убран kernel_initializer, так что по умолчанию он будет glorot_uniform):

model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='relu', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))

Обучается чудесно:

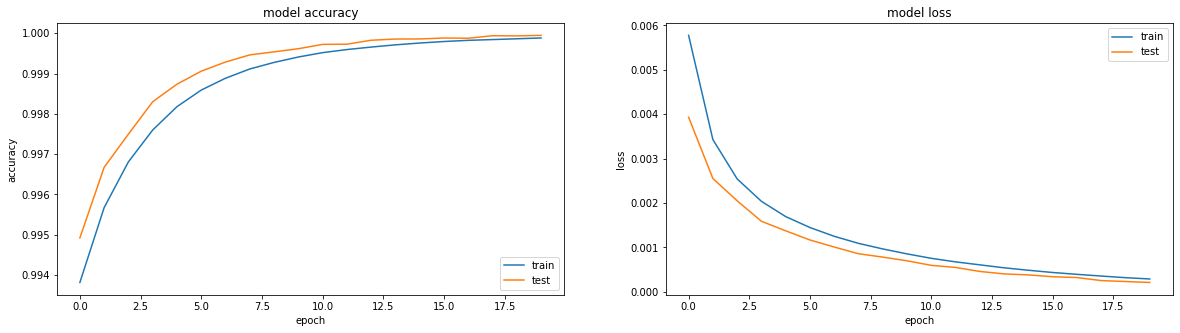
Результат получался вполне себе неплохой, accuracy: 0.9999, loss(mse): 2e-04 после 20 эпох и можно тренировать дальше.

Дальше попробуем с сигмойдом:

model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='sigmoid', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))

Что-то похожее я уже обучал раньше, с единственной разницей — здесь отключен bias. Обучается меееедленно, выходит на плато в районе 50й эпохи, accuracy: 0.9970, loss: 0.01 после 60 эпох.

Результат опять не впечатляет:

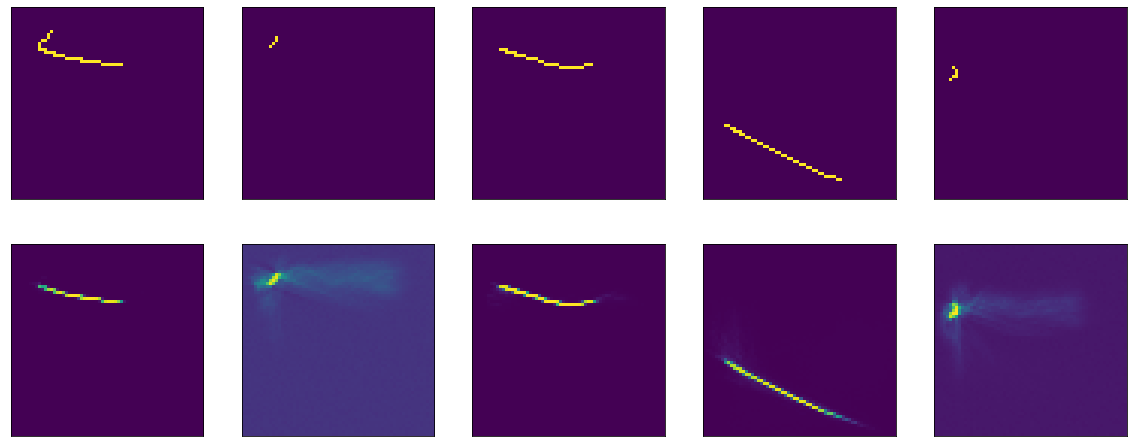
Ну и еще проверим tanh:

model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='tanh', use_bias=False)) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))

Результат сравним с relu — accuracy: 0.9999, loss: 6e-04 после 20 эпох, причем можно тренировать дальше:

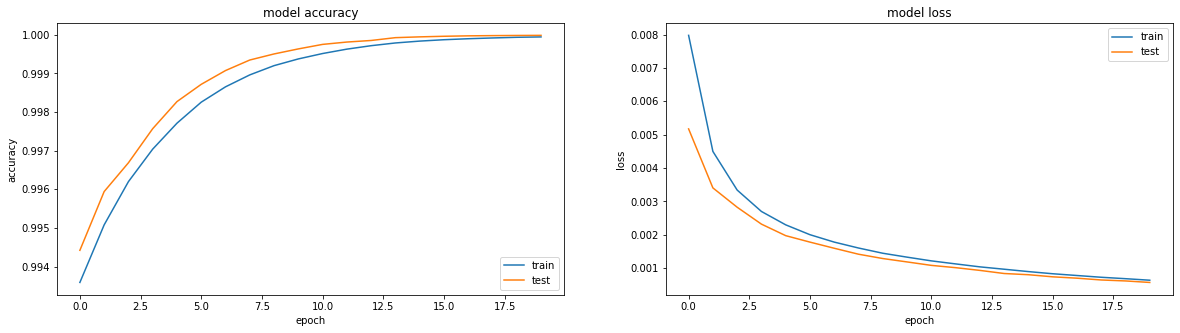
На самом деле меня мучает вопрос, можно ли что-то сделать, чтобы sigmoid показал сравнимый результат. Исключительно из спортивного интереса.

Например, можно попробовать добавить BatchNormalization:

model = tf.keras.Sequential() model.add(tf.keras.Input(shape=(64,64,1))) model.add(tf.keras.layers.Flatten()) model.add(tf.keras.layers.Dense(64*64, activation='sigmoid', use_bias=False)) model.add(tf.keras.layers.BatchNormalization()) model.add(tf.keras.layers.Reshape(target_shape=(64,64,1)))

И тут случается какая-то магия. На 13й эпохе accuracy: 1.0. И результаты огненные:

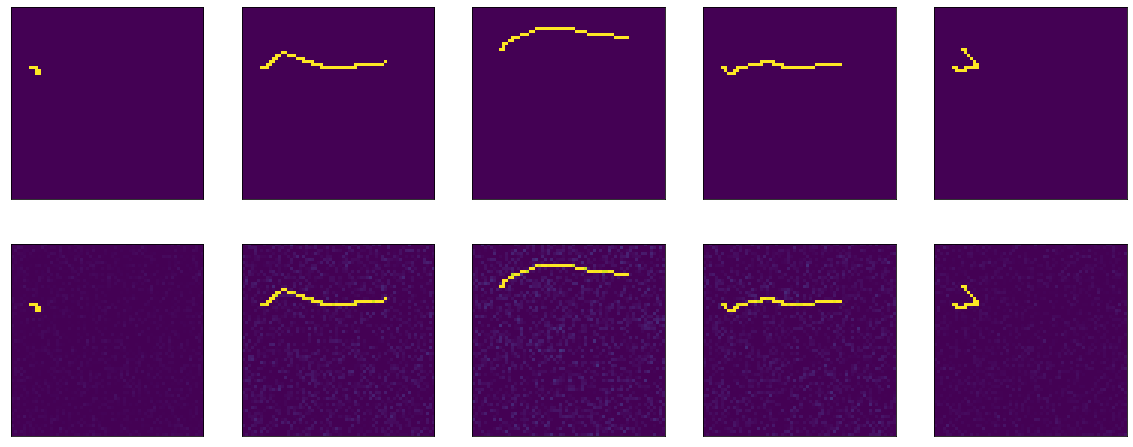
Иииии… на этом cliff-hanger'е я закончу первую часть, ибо получилось уже слишком дофига текста, да и не понятно, надо оно кому-то или нет. Во второй части буду разбираться, что за магия случилась, экспериментировать с разными оптимизаторами, пробовать построить уже энкодер-декодер честный, биться головой об стол. Надеюсь, кому-нибудь было интересно и полезно.