
Если мы говорим о математике в контексте Data Science, мы можем выделить три наиболее часто решаемые задачи (хотя задач, разумеется, больше):

- Задача регрессионного анализа или выявления зависимостей (когда у нас есть некий набор наблюдений). На графике выше вы можете увидеть, что есть некая переменная х и некая переменная у, и мы наблюдаем значения у при конкретном х. Мы знаем эти точки и знаем их координаты, а также знаем, что х как-то влияет на y, то есть эти две переменные зависимы между собой. Естественно, мы хотим вычислить уравнение их зависимости — для этого используется модель классической парной линейной регрессии, когда предполагается, что их зависимость может быть описана некой прямой линией. Соответственно, дальше коэффициенты прямой линии подбираются так, чтобы минимизировать ошибку описания данных. И вот как раз от того, какая ошибка (метрика качества) будет выбрана, зависит фактический результат построения линейной регрессии.
- Другая задача из анализа данных — рекомендательные системы. Это когда мы говорим, что есть, к примеру, онлайн-магазины, в них есть некий набор товаров, а человек совершает покупки. На основании этой информации можно в векторном пространстве представить описание этого человека, и, построив это векторное пространство, построить в дальнейшем математическую зависимость того, с какой вероятностью этот человек купит тот или иной товар, зная его предыдущие покупки. Соответственно, речь идёт о классификации, когда мы классифицируем потенциальных покупателей по принципам: «купит-не купит», «интересно-неинтересно» и т. д. Здесь есть различные подходы: user-based и item-based.
- Третья область — компьютерное зрение. В ходе этой задачи мы пытаемся определить, где располагается интересный нам объект. Это фактически является решением задачи минимизации ошибки путём выбора конкретных пикселей, которые формируют картинку объекта.
Во всех трёх задачах присутствует и оптимизация, и минимизация ошибки, и наличие той или иной модели, которая описывает зависимость переменных. При этом внутри каждой лежит представление данных, которые разложены на векторное описание. Мы же в нашей статье уделим особое внимание разделу, который затрагивает именно регрессионные модели.
Мы уже упомянули, что есть некий набор пар данных: Х и Y. Мы знаем, какие значения принимает Y относительно X. Если Х — это время, то тогда у нас получается модель временного ряда, в котором Y — это, допустим, цена нефти и при этом курс рубля к доллару, а Х — это некоторый период времени с 2014 по 2018:
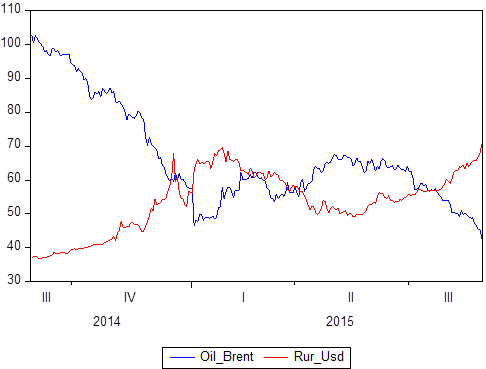
Рассмотрим следующую иллюстрацию:
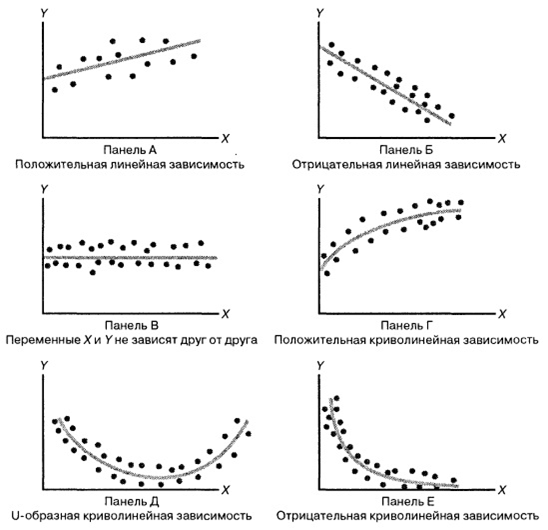
Получается, мы выбираем какую-то модель зависимости данных, а виды зависимости между случайными величинами бывают разные. Всё не так уж и очевидно, ведь даже на этих простых рисунках мы видим различные зависимости. Выбрав конкретную зависимость, мы сможем использовать регрессионные методы для калибровки модели.
От того, какую модель вы выберете, будет зависеть качество ваших прогнозов. Если остановиться на линейных регрессионных моделях, то мы предполагаем, что есть некий набор реальных значений:

Точки R1, R2, R3, R4 — это значения, которые выдаёт наша модель при значениях X. Что получается? Точки P — точки, которые мы реально наблюдаем (реально собрали), а точки R — это точки, которые мы наблюдаем в нашей модели (те, что она выдаёт). Дальше следует до безумия простая человеческая логика: модель будет считаться качественной тогда и только тогда, когда точки R максимально близки к точкам P.
Если мы построим расстояние между этими точками для одинаковых «иксов» (P1 – R1, P2 – R2 и т. д.), то мы получим то, что называется ошибками линейной регрессии. Мы получим отклонения в линейной регрессии, и эти отклонения называются U1, U2, U3…Un. А ошибки эти могут быть как в плюс, так и в минус (мы могли переоценить или недооценить). Чтобы эти отклонения сравнить, их нужно проанализировать. Здесь применяют очень большой и красивый способ — возведение в квадрат (возведение в квадрат «убивает» знак). А сумму квадратов всех отклонений в математической статистике называют RSS (Residual Sum of Squares). Минимизировав RSS по b1 и минимизировав RSS по b2, мы получаем оптимальные коэффициенты, которые фактически выводятся методом наименьших квадратов.
После того, как мы построили регрессию, определили оптимальные коэффициенты b1 и b2, и у нас есть уравнение регрессии, проблемы на этом не заканчиваются, а задача продолжает развиваться. Дело в том, что если на одном графике пометить саму регрессию, все значения, которые у нас есть, а также средние значения «игреков», то суммы квадратов ошибок можно будет доуточнить.
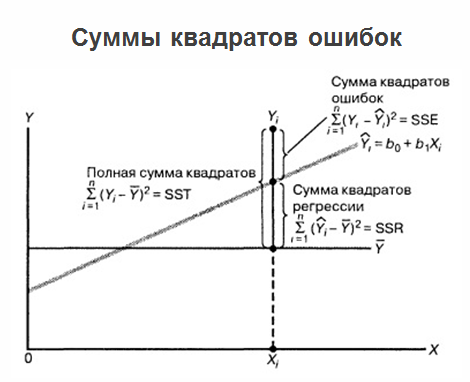

По анализу ошибок можно даже сразу понять, где просчитались, какой тип ошибки сделали. И вот здесь нельзя не упомянуть теорему Гаусса-Маркова:

Вывод можно сделать следующий: сейчас мы понимаем, что область построения регрессионной модели — это, в каком-то смысле, кульминация с точки зрения математики, потому что в ней сливаются сразу все возможные разделы, которые могут быть полезны в анализе данных, например:
- линейная алгебра со способами представления данных;
- математический анализ с теорией оптимизации и средствами анализа функций;
- теория вероятности со средствами описания случайных событий и величин и моделирования зависимости между переменными.
Коллеги, предлагаю всё-таки не ограничиваться чтением и посмотреть вебинар целиком. В статью не вошли моменты, связанные с линейным программированием, оптимизацией в регрессионных моделях и другими деталями, которые могут быть вам полезны.