Нейросеть выучивает базовые физические законы

Исследователи из Uber AI предложили архитектуру нейросети, которая выучивает физические законы. Модель протестировали на задаче предсказания наблюдений системы массы-пружины. В сравнении с стандартной архитектурой нейросети Гамильтовы нейросети обладают большей обобщающей способности и обучаются быстрее.

Масса-пружина — это частный случай гармонического осциллятора, системы, которая при выведении её из положения равновесия испытывает действие возвращающей силы.

Несмотря на то, что нейросети нашли широкое применение, они не справляются с задачей понимания базовых законом физики. Чтобы улучшить обобщающую способность нейросетей в применении к физическим задачам, исследователи предложили Hamiltonian архитектуру нейросети (HNN). Они опирались на Гамильтонову механику при обучении моделей. Такой подход позволяет нейросети выучить и использовать законы сохранения без использования размеченных данных во время обучения. HNNs являются общей архитектурой для обучения физическим законам. Это связано с тем, что большинство физических законов может быть выражено в законах сохранения.

Исследователи оценивают модели на задачах, где важно сохранение энергии. Среди них задача двух тел и пиксельные наблюдения маятника. Особенностью модели является ее обратимость по времени. 

Данные для обучения

Модели были обучены на трех простых физических задачах:

1. Идеальный случай системы с пружиной и массой: обучающий и тестовый наборы данных состояли из 25 траекторий и гауссовского шума;
2. Идеальный случай маятника: обучающий и тестовый датасеты собирались аналогично первой задаче;
3. Реальный маятник: взяли готовый датасет из реального мира, чтобы проверить, как HNN справляются с реальными данными, в которых больше шума, чем в синтетических

В качестве функции потерь при обучении использовалась среднеквадратичная ошибка (MSE) между реальными и предсказанными энергиями.

Тестирование моделей

Ниже видно результаты сравнений стандартной нейросети и HNN на трех базовых задачах. Сравниваются предсказания, MSE между реальными и предсказанными координатами и метрики энергии. Видно, что HNN выдают более приближенные к реальным данным результаты, чем стандартная нейросеть.

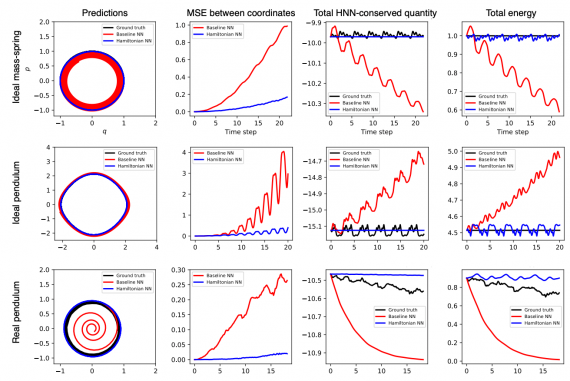Результаты сравнений HNN и стандартной нейросети

Источник: neurohive.io

Комментарии: