Свёрточная нейронная сеть с нуля. Часть 2. Слой подвыборки

В прошлой статье мы создали свёрточный слой, научились считать градиенты при обратном распространении ошибки и обновлять весовые коэффициенты для уменьшения функции потерь. Сегодня мы разберёмся с тем, как уменьшается пространственная размерность входной карты признаков и как рассчитываются градиенты слоя пулинга. Помимо этого мы рассмотрим различные типы пулинга и решим, в какой ситуации лучше использовать каждый из них. Но для начала, давайте разберёмся, как вообще работает слой пулинга и какие его версии существуют.

Зачем нужен пулинг

Основной задачей слоя подвыборки является снижение размерности входного тензора, что позволяет сократить количество дальнейших вычислений. Помимо этого, подобное уменьшение размерности позволяет сети быть более устойчивой к небольшим сдвигам объектов на изображении.

Какой бывает пулинг

Способов уменьшить размерность пространства карт особенностей на самом деле может быть весьма много: можно выбирать максимальные значения (макспулинг), можно усреднять значения (средний пулинг), брать сумму (пулинг суммы) или вовсе взять минимум. Чаще всего в свёрточных сетях в слое подвыборки используется макспулинг, как хорошо зарекомендовавший себя в многочисленных исследованиях. Чтобы лучше понимать, как влияет на выходное изображение различные типы пулинга, мы предлагаем самостоятельно выбрать тип подвыборки в интерактивном примере ниже:

Если же пример с изображением кажется слишком неочевидным, то, надеемся, расположенная ниже гифка поможет разобраться с работой слоя подвыборки:

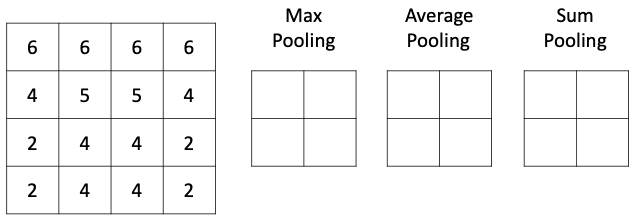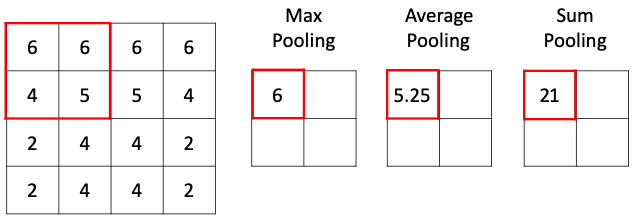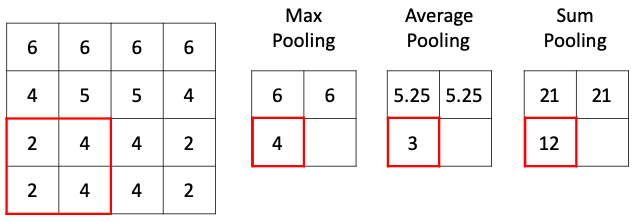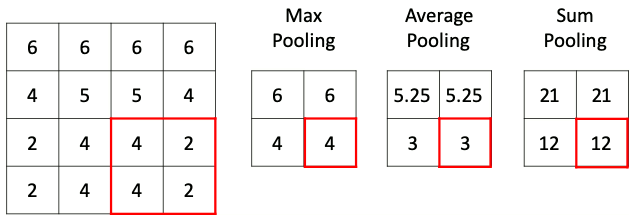
Различные типы пулинга

Пишем слой пулинга

Мы подробно опишем только класс макспулинга, поскольку другие типы уменьшения пространственной размерности работают полностью аналогично, и вам не составит труда создать их самостоятельно. Как было сказано выше, слой подвыборки уменьшает пространственную размерность входных карт признаков в несколько раз (обычно в 2), а значит нам потребуется хранить в классе коэффициент уменьшения. Создадим заготовку для класса макспулинга:

  class MaxPoolingLayer {      TensorSize inputSize; // размер входа      TensorSize outputSize; // размер выхода            int scale; // во сколько раз уменьшается размерность    public:      MaxPoolingLayer(TensorSize size, int scale = 2); // создание слоя        Tensor Forward(const Tensor &X); // прямое распространение      Tensor Backward(const Tensor &dout, const Tensor &X); // обратное распространение  };  

Как и свёрточный слой, слой макспулинга создаётся крайне просто: нужно всего лишь запомнить входной размер и коэффициент уменьшения размерности, а затем расчитать размер выходного тензора:

  MaxPoolingLayer::MaxPoolingLayer(TensorSize size, int scale) {      // запоминаем входной размер      inputSize.width = size.width;      inputSize.height = size.height;      inputSize.deep = size.deep;        // вычисляем выходной размер      outputSize.width = size.width / scale;      outputSize.height = size.height / scale;      outputSize.deep = size.deep;        this->scale = scale; // запоминаем коэффициент уменьшения  }  

Прямое распространение сигнала

Описав создание слоя, перейдём к написанию прямого распространения. Для получения выходного тензора необходимо пройтись по всем подматрицам размера scale x scale входного объёма, найти максимум в них и записать его в выходной тензор:

  // прямое распространение  Tensor MaxPoolingLayer::Forward(const Tensor &X) {      Tensor output(outputSize); // создаём выходной тензор        // проходимся по каждому из каналов      for (int d = 0; d < inputSize.deep; d++) {          for (int i = 0; i < inputSize.height; i += scale) {              for (int j = 0; j < inputSize.width; j += scale) {                  double max = X(d, i, j); // начальное значение максимума - значение первой клетки подматрицы                    // проходимся по подматрице и ищем максимум и его координаты                  for (int y = i; y < i + scale; y++) {                      for (int x = j; x < j + scale; x++) {                          double value = X(d, y, x); // получаем значение входного тензора                            // если очередное значение больше максимального                          if (value > max)                              max = value; // обновляем максимум                      }                  }                    output(d, i / scale, j / scale) = max; // записываем в выходной тензор найденный максимум              }          }      }        return output; // возвращаем выходной тензор  }  

Обратное распространение ошибки

Обратное распространение в слое макс пулинга производится довольно просто: так как при прямом проходе на выход пошёл лишь один элемент, то при обратном распространении полученное значение градиента следующего слоя нужно записать в место расположения максимального элемента. Получается, нам нужно знать, в каком месте находился максимальный элемент. Есть несколько способов сделать это: можно сравнивать полученные значения при прямом распространении со значениями на входе, а можно создать бинарную маску, где каждый элемент будет равен единице, если в заданной клетке расположен максимум, и нулю в противном случае. Данную маску можно посчитать при прямом проходе, а при обратном распространении ошибки умножить её на градиенты следующего слоя.

Поскольку каждый канал обрабатывается независимо, то и масок у нас должно получиться столько же, сколько и каналов во входном тензоре. Поэтому добавим в класс тензор mask и при создании класса зададим создадим его по размеру входной карты признаков. Метод прямого распространения будет слегка модифицирован:

  // прямое распространение с использованием маски  Tensor MaxPoolingLayer::Forward(const Tensor &X) {      Tensor output(outputSize); // создаём выходной тензор        // проходимся по каждому из каналов      for (int d = 0; d < inputSize.deep; d++) {          for (int i = 0; i < inputSize.height; i += scale) {              for (int j = 0; j < inputSize.width; j += scale) {                  int imax = i; // индекс строки максимума                  int jmax = j; // индекс столбца максимума                  double max = X(d, i, j); // начальное значение максимума - значение первой клетки подматрицы                    // проходимся по подматрице и ищем максимум и его координаты                  for (int y = i; y < i + scale; y++) {                      for (int x = j; x < j + scale; x++) {                          double value = X(d, y, x); // получаем значение входного тензора                          mask(d, y, x) = 0; // обнуляем маску                            // если входное значение больше максимального                          if (value > max) {                              max = value; // обновляем максимум                              imax = y; // обновляем индекс строки максимума                              jmax = x; // обновляем индекс столбца максимума                          }                      }                  }                    output(d, i / scale, j / scale) = max; // записываем в выходной тензор найденный максимум                  mask(d, imax, jmax) = 1; // записываем 1 в маску в месте расположения максимального элемента              }          }      }        return output; // возвращаем выходной тензор  }  

Как мы выяснили выше, обратное распространение ошибки для слоя макспулинга сводится к умножению градиентов следующего слоя на рассчитанную маску. Обратное распространение ошибки будет выглядеть следующим образом:

  // обратное распространение  Tensor MaxPoolingLayer::Backward(const Tensor &dout, const Tensor &X) {      Tensor dX(inputSize); // создаём тензор для градиентов        for (int d = 0; d < inputSize.deep; d++)          for (int i = 0; i < inputSize.height; i++)              for (int j = 0; j < inputSize.width; j++)                  dX(d, i, j) = dout(d, i / scale, j / scale) * mask(d, i, j); // умножаем градиенты на маску        return dX; // возвращаем посчитанные градиенты  }  

Заметим, что для пулинга среднего и пулинга суммы не требуется добавление бинарной маски, так как в них при обратном распространении градиенты следующего слоя просто копируются во все элементы соответствующих подматриц (для среднего градиенты делятся на общее количество элементов подматрицы).

Полный код слоя

  #include "Tensor.hpp"    class MaxPoolingLayer {      TensorSize inputSize; // размер входа      TensorSize outputSize; // размер выхода            int scale; // во сколько раз уменьшается размерность      Tensor mask; // маска для максимумов    public:      MaxPoolingLayer(TensorSize size, int scale = 2); // создание слоя        Tensor Forward(const Tensor &X); // прямое распространение      Tensor Backward(const Tensor &dout, const Tensor &X); // обратное распространение  };    // создание слоя  MaxPoolingLayer::MaxPoolingLayer(TensorSize size, int scale) : mask(size) {      // запоминаем входной размер      inputSize.width = size.width;      inputSize.height = size.height;      inputSize.deep = size.deep;        // вычисляем выходной размер      outputSize.width = size.width / scale;      outputSize.height = size.height / scale;      outputSize.deep = size.deep;        this->scale = scale; // запоминаем коэффициент уменьшения  }    // прямое распространение с использованием маски  Tensor MaxPoolingLayer::Forward(const Tensor &X) {      Tensor output(outputSize); // создаём выходной тензор        // проходимся по каждому из каналов      for (int d = 0; d < inputSize.deep; d++) {          for (int i = 0; i < inputSize.height; i += scale) {              for (int j = 0; j < inputSize.width; j += scale) {                  int imax = i; // индекс строки максимума                  int jmax = j; // индекс столбца максимума                  double max = X(d, i, j); // начальное значение максимума - значение первой клетки подматрицы                    // проходимся по подматрице и ищем максимум и его координаты                  for (int y = i; y < i + scale; y++) {                      for (int x = j; x < j + scale; x++) {                          double value = X(d, y, x); // получаем значение входного тензора                          mask(d, y, x) = 0; // обнуляем маску                            // если входное значение больше максимального                          if (value > max) {                              max = value; // обновляем максимум                              imax = y; // обновляем индекс строки максимума                              jmax = x; // обновляем индекс столбца максимума                          }                      }                  }                    output(d, i / scale, j / scale) = max; // записываем в выходной тензор найденный максимум                  mask(d, imax, jmax) = 1; // записываем 1 в маску в месте расположения максимального элемента              }          }      }        return output; // возвращаем выходной тензор  }    // обратное распространение  Tensor MaxPoolingLayer::Backward(const Tensor &dout, const Tensor &X) {      Tensor dX(inputSize); // создаём тензор для градиентов        for (int d = 0; d < inputSize.deep; d++)          for (int i = 0; i < inputSize.height; i++)              for (int j = 0; j < inputSize.width; j++)                  dX(d, i, j) = dout(d, i / scale, j / scale) * mask(d, i, j); // умножаем градиенты на маску        return dX; // возвращаем посчитанные градиенты  }  

Итоги

Мы рассмотрели принципы работы различных типов пулинга и реализовали класс для макспулинга с возможностью задавать коэффициент уменьшения размерности. Теперь в нашем распоряжении уже два основных слоя из четырёх. В следующей части мы расскажем, как создать слой активации, а также рассмотрим наиболее часто используемые активационные функции.

Источник: programforyou.ru

Комментарии: