Стохастический градиентный спуск(SGD) для логарифмической функции потерь(LogLoss) в задаче бинарной классификации

Предыдущая часть (про линейную регрессию, градиентный спуск и про то, как оно всё работает) — habr.com/ru/post/471458
В этой статье я покажу решение задачи классификации сначала, что называется, «ручками», без сторонних библиотек для SGD, LogLoss'а и вычисления градиентов, а затем с помощью библиотеки PyTorch.
Задача: для двух категориальных признаков, описывающих желтизну и симметричность, определить, к какому из классов (яблоко или груша) относится объект (обучить модель классифицировать объекты).

Для начала загрузим наш датасет:

import pandas as pd data = pd.read_csv("https://raw.githubusercontent.com/DLSchool/dlschool_old/master/materials/homeworks/hw04/data/apples_pears.csv") data.head(10)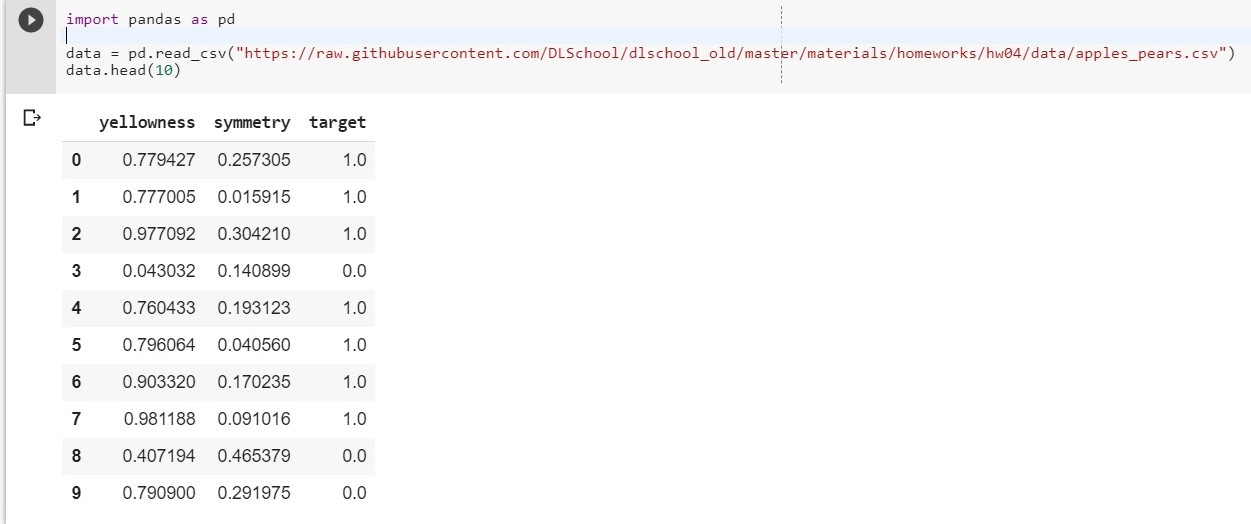

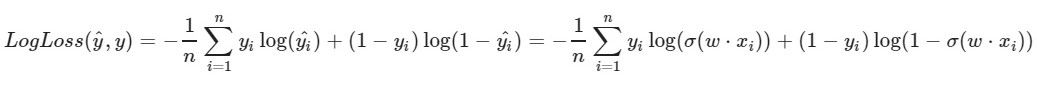
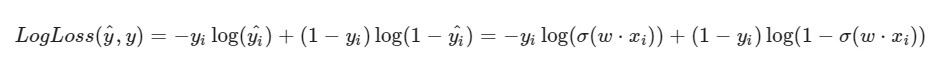
Пусть: x1 — yellowness, x2 — symmetry, y = targer Составим функцию y = w1 * x1 + w2 * x2 + w0 (w0 будем считать смещением(англ. — bias)) Теперь наша задача сводится к поиску весов w1, w2 и w0, которые наиболее точным образом описывают зависимость y от x1 и x2. Используем логарифмическую функцию потерь:

Левый параметр функции — предсказание с текущими весами w1, w2, w0 Правый параметр функции — правильное значение(класс — 0 или 1) ?(x) — сигмоидная функция активации от x log(x) — натуральный логарифм от x Понятно, что чем меньше значение функции потерь, тем лучше мы подобрали веса w1, w2, w0. Для этого выберем стохастический градиентный спуск. Подмечу, что формула для LogLoss'а примет другой вид в виду того, что в SGD мы выбираем один элемент, а не целую выборку(или подвыборку как в случае с mini-batch gradient descent):

Ход решения:

Начальным весам w1, w2, w0 зададим рандомные значения

Мы берем некий i-ый объект нашего датасета(допустим, рандомный), вычисляем для него LogLoss(с нашими w1, w2 и w0, которым мы изначально присвоили рандомные значения), потом вычисляем частные производные по каждому из весов w1, w2 и w0, затем обновляем каждый из весов.

Небольшая подготовка:

import pandas as pd import numpy as np  X = data.iloc[:,:2].values  # матрица объекты-признаки y = data['target'].values.reshape((-1, 1))  # классы (столбец из нулей и единиц)  x1 = X[:, 0] x2 = X[:, 1]  def sigmoid(x):     return 1 / (1 + np.exp(-x))

Реализация:

import random np.random.seed(62) w1 = np.random.randn(1) w2 = np.random.randn(1) w0 = np.random.randn(1)  print(w1, w2, w0)  # form range 0..999 idx = np.arange(1000)  # random shuffling np.random.shuffle(idx) x1, x2, y = x1[idx], x2[idx], y[idx] # learning rate lr = 0.001  # number of epochs n_epochs = 10000  for epoch in range(n_epochs):   yhat = w1 * x1[0] + w2 * x2[0] + w0      i = random.randint(0, 999)      w1_grad = -((y[i] - sigmoid(yhat)) * x1[i])      w2_grad = -((y[i] - sigmoid(yhat)) * x2[i])      w0_grad = -(y[i] - sigmoid(yhat))      w1 -= lr * w1_grad      w2 -= lr * w2_grad      w0 -= lr * w0_grad   print(w1, w2, w0) 

[-0.01232543] [-0.52758101] [-0.2875912]
[1.04580084] [-1.44782108] [0.09686356]

*_grad — производная по соответствующему весу. Распишу общую формулу:

Для свободного члена w0 — опускается множитель x(принимается равным единице). По итоговой формуле производной можно заметить, что нам не требуется вычислять в явном виде функцию потерь(нам нужны лишь частные производные). Проверим, на скольких объектах из обучающей выборки наша модель даёт верные ответы, а на скольких — неверные.

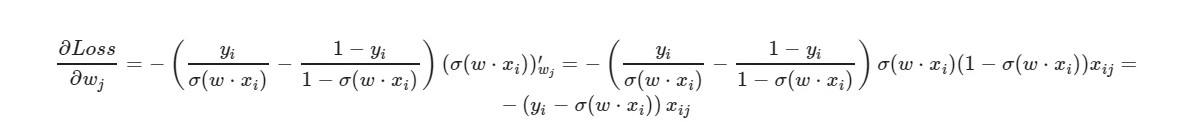
i = 0 correct = 0 incorrect = 0 for item in y:   if(np.around(x1[i] * w1 + x2[i] * w2 + w0) == item):     correct += 1   else:     incorrect += 1   i = i + 1  print(correct, incorrect)

857 143

np.around(x) — округляет значение x. Для нас: если x > 0.5, то значение равно 1. Если x ? 0.5, то значение равно 0.

А что мы будем делать, если кол-во признаков у объекта будет равно 5? 10? 100? И весов у нас будет соответствующее количество(плюс один для bias'а). Понятное дело, что вручную работать с каждым весом, вычислять для него градиенты неудобно.

Воспользуемся популярной библиотекой PyTorch.

PyTorch=NumPy+CUDA+Autograd(автоматическое вычисление градиентов) Реализация с помощью PyTorch:

import torch import numpy as np  from torch.nn import Linear, Sigmoid  def make_train_step(model, loss_fn, optimizer):     def train_step(x, y):         model.train()         yhat = model(x)         loss = loss_fn(yhat, y)         loss.backward()         optimizer.step()         optimizer.zero_grad()         return loss.item()     return train_step  X = torch.FloatTensor(data.iloc[:,:2].values)     y = torch.FloatTensor(data['target'].values.reshape((-1, 1)))  from torch import optim, nn  neuron = torch.nn.Sequential(     Linear(2, out_features=1),     Sigmoid() ) print(neuron.state_dict())  lr = 0.1 n_epochs = 10000 loss_fn = nn.MSELoss(reduction="mean") optimizer = optim.SGD(neuron.parameters(), lr=lr) train_step = make_train_step(neuron, loss_fn, optimizer)  for epoch in range(n_epochs):     loss = train_step(X, y)      print(neuron.state_dict()) print(loss)

OrderedDict([('0.weight', tensor([[-0.4148, -0.5838]])), ('0.bias', tensor([0.5448]))])
OrderedDict([('0.weight', tensor([[ 5.4915, -8.2156]])), ('0.bias', tensor([-1.1130]))])
0.03930133953690529

Достаточно неплохой лосс на тестовой выборке.

Здесь в качестве функции потерь выбрана MSELoss. Подробнее про Linear Вкратце: мы подаем 2 параметра на вход(наши x1 и x2 как в предыдущем примере) и получаем на выход один параметр(y), который, в свою очередь, подаем на вход функции активации. А дальше уже вычисляются: значение функции ошибок, градиенты. В конце — обновляются веса. Материалы, используемые в статье