Машинное обучение для начинающих: создание нейронных сетей

2019-10-12 07:39

Далее будет представлено максимально простое объяснение того, как работают нейронные сети, а также показаны способы их реализации в Python. Приятная новость для новичков – нейронные сети не такие уж и сложные. Термин нейронные сети зачастую используют в разговоре, ссылаясь на какой-то чрезвычайно запутанный концепт. На деле же все намного проще.

Данная статья предназначена для людей, которые ранее не работали с нейронными сетями вообще или же имеют довольно поверхностное понимание того, что это такое. Принцип работы нейронных сетей будет показан на примере их реализации через Python.

Содержание статьи

Создание нейронных блоков
Простой пример работы с нейронами в Python
Создание нейрона с нуля в Python
Пример сбор нейронов в нейросеть
Пример прямого распространения FeedForward
Создание нейронной сети прямое распространение FeedForward
Пример тренировки нейронной сети — минимизация потерь, Часть 1
Пример подсчета потерь в тренировки нейронной сети
Python код среднеквадратической ошибки (MSE)
Тренировка нейронной сети — многовариантные исчисления, Часть 2
Пример подсчета частных производных
Тренировка нейронной сети: Стохастический градиентный спуск
Создание нейронной сети с нуля на Python

Создание нейронных блоков

Для начала необходимо определиться с тем, что из себя представляют базовые компоненты нейронной сети – нейроны. Нейрон принимает вводные данные, выполняет с ними определенные математические операции, а затем выводит результат. Нейрон с двумя входными данными выглядит следующим образом:

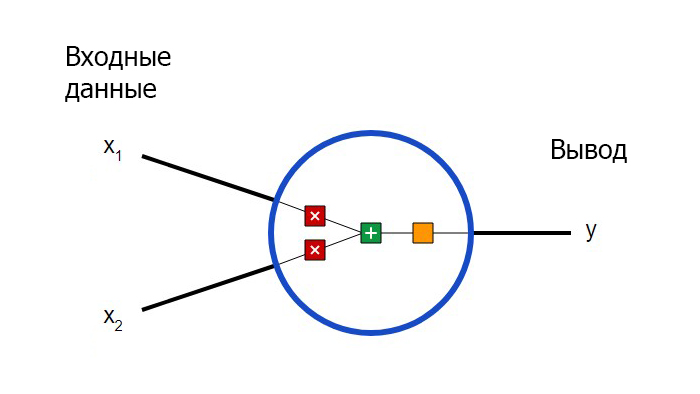
Здесь происходят три вещи. Во-первых, каждый вход умножается на вес (на схеме обозначен красным):

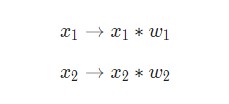
Создание нейронных блоков

Затем все взвешенные входы складываются вместе со смещением b (на схеме обозначен зеленым):

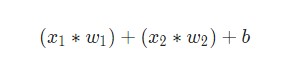
neural-networks-3

Наконец, сумма передается через функцию активации (на схеме обозначена желтым):

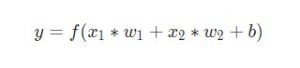
Функция активации используется для подключения несвязанных входных данных с выводом, у которого простая и предсказуемая форма. Как правило, в качестве используемой функцией активации берется функция сигмоида:

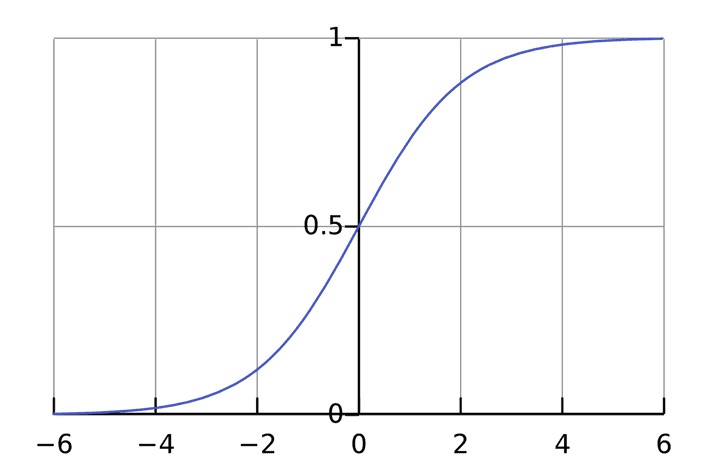
Функция сигмоида выводит только числа в диапазоне (0, 1). Вы можете воспринимать это как компрессию от (??, +?) до (0, 1). Крупные отрицательные числа становятся ~0, а крупные положительные числа становятся ~1.

Простой пример работы с нейронами в Python

Предположим, у нас есть нейрон с двумя входами, который использует функцию активации сигмоида и имеет следующие параметры:

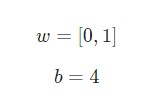
формулы функции сигмоида

w = [0,1] — это просто один из способов написания w₁= 0, w₂= 1 в векторной форме. Присвоим нейрону вход со значением x = [2, 3]. Для более компактного представления будет использовано скалярное произведение.

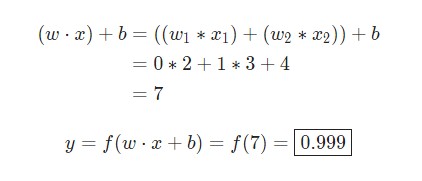
С учетом, что вход был x = [2, 3], вывод будет равен 0.999. Вот и все. Такой процесс передачи входных данных для получения вывода называется прямым распространением, или feedforward.

Создание нейрона с нуля в Python

Мы собрали ТОП Книг для Python программиста которые помогут быстро изучить язык программирования Python. Список книг: Книги по Python

Приступим к имплементации нейрона. Для этого потребуется использовать NumPy. Это мощная вычислительная библиотека Python, которая задействует математические операции:

Python

importnumpy asnp

defsigmoid(x):

# Наша функция активации: f(x) = 1 / (1 + e^(-x))

return1/(1+np.exp(-x))

classNeuron:

def__init__(self,weights,bias):

self.weights=weights

self.bias=bias

deffeedforward(self,inputs):

# Вводные данные о весе, добавление смещения

# и последующее использование функции активации

total=np.dot(self.weights,inputs)+self.bias

returnsigmoid(total)

weights=np.array([0,1])# w1 = 0, w2 = 1

bias=4# b = 4

n=Neuron(weights,bias)

x=np.array([2,3])# x1 = 2, x2 = 3

print(n.feedforward(x))# 0.9990889488055994

Узнаете числа? Это тот же пример, который рассматривался ранее. Ответ полученный на этот раз также равен 0.999.

Пример сбор нейронов в нейросеть

Нейронная сеть по сути представляет собой группу связанных между собой нейронов. Простая нейронная сеть выглядит следующим образом:

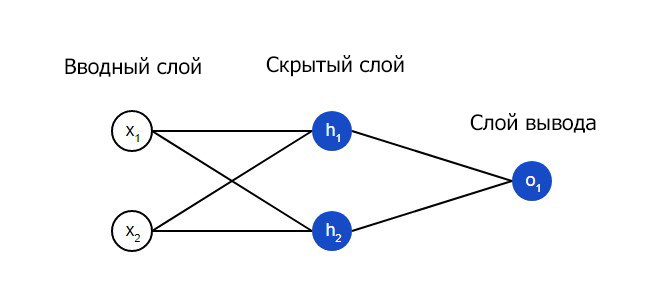
На вводном слое сети два входа – x₁ и x₂. На скрытом слое два нейтрона — h₁ и h₂. На слое вывода находится один нейрон – о₁. Обратите внимание на то, что входные данные для о₁ являются результатами вывода h₁ и h₂. Таким образом и строится нейросеть.

Скрытым слоем называется любой слой между вводным слоем и слоем вывода, что являются первым и последним слоями соответственно. Скрытых слоев может быть несколько.

Пример прямого распространения FeedForward

Давайте используем продемонстрированную выше сеть и представим, что все нейроны имеют одинаковый вес w = [0, 1], одинаковое смещение b = 0 и ту же самую функцию активации сигмоида. Пусть h₁, h₂ и o₁ сами отметят результаты вывода представленных ими нейронов.

Что случится, если в качестве ввода будет использовано значение х = [2, 3]?

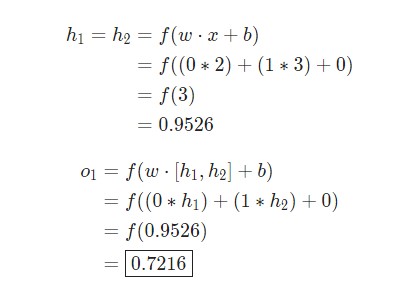
Пример прямого распространения feedforward

Результат вывода нейронной сети для входного значения х = [2, 3] составляет 0.7216. Все очень просто.

Нейронная сеть может иметь любое количество слоев с любым количеством нейронов в этих слоях.

Суть остается той же: нужно направить входные данные через нейроны в сеть для получения в итоге выходных данных. Для простоты далее в данной статье будет создан код сети, упомянутая выше.

Создание нейронной сети прямое распространение FeedForward

Далее будет показано, как реализовать прямое распространение feedforward в отношении нейронной сети. В качестве опорной точки будет использована следующая схема нейронной сети:

Python

importnumpy asnp

# ... Здесь код из предыдущего раздела

classOurNeuralNetwork:

"""

Нейронная сеть, у которой:

- 2 входа

- 1 скрытый слой с двумя нейронами (h1, h2)

- слой вывода с одним нейроном (o1)

У каждого нейрона одинаковые вес и смещение:

- w = [0, 1]

- b = 0

"""

def__init__(self):

weights=np.array([0,1])

bias=0

# Класс Neuron из предыдущего раздела

self.h1=Neuron(weights,bias)

self.h2=Neuron(weights,bias)

self.o1=Neuron(weights,bias)

deffeedforward(self,x):

out_h1=self.h1.feedforward(x)

out_h2=self.h2.feedforward(x)

# Вводы для о1 являются выводами h1 и h2

out_o1=self.o1.feedforward(np.array([out_h1,out_h2]))

returnout_o1

network=OurNeuralNetwork()

x=np.array([2,3])

print(network.feedforward(x))# 0.7216325609518421

Мы вновь получили 0.7216. Похоже, все работает.

Пример тренировки нейронной сети — минимизация потерь, Часть 1

Предположим, у нас есть следующие параметры:

Имя/Name Вес/Weight (фунты) Рост/Height (дюймы) Пол/Gender
Alice 133 65 F
Bob 160 72 M
Charlie 152 70 M
Diana 120 60 F

Давайте натренируем нейронную сеть таким образом, чтобы она предсказывала пол заданного человека в зависимости от его веса и роста.

Мужчины Male будут представлены как 0, а женщины Female как 1. Для простоты представления данные также будут несколько смещены.

Имя/Name Вес/Weight (минус 135) Рост/Height (минус 66) Пол/Gender
Alice -2 -1 1
Bob 25 6 0
Charlie 17 4 0
Diana -15 -6 1

Для оптимизации здесь произведены произвольные смещения 135 и 66. Однако, обычно для смещения выбираются средние показатели.

Потери

Перед тренировкой нейронной сети потребуется выбрать способ оценки того, насколько хорошо сеть справляется с задачами. Это необходимо для ее последующих попыток выполнять поставленную задачу лучше. Таков принцип потери.

В данном случае будет использоваться среднеквадратическая ошибка (MSE) потери:

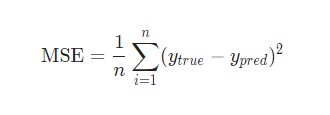
Давайте разберемся:

n – число рассматриваемых объектов, которое в данном случае равно 4. Это Alice, Bob, Charlie и Diana;
y – переменные, которые будут предсказаны. В данном случае это пол человека;
y_true – истинное значение переменной, то есть так называемый правильный ответ. Например, для Alice значение y_true будет 1, то есть Female;
y_pred – предполагаемое значение переменной. Это результат вывода сети.

(y_true - y_pred)² называют квадратичной ошибкой (MSE). Здесь функция потери просто берет среднее значение по всем квадратичным ошибкам. Отсюда и название ошибки. Чем лучше предсказания, тем ниже потери.

Лучшие предсказания = Меньшие потери.

Тренировка нейронной сети = стремление к минимизации ее потерь.

Пример подсчета потерь в тренировки нейронной сети

Скажем, наша сеть всегда выдает 0. Другими словами, она уверена, что все люди — Мужчины. Какой будет потеря?

Имя/Name y_true y_pred (y_true — y_pred)²
Alice 1 0 1
Bob 0 0 0
Charlie 0 0 0
Diana 1 0 1

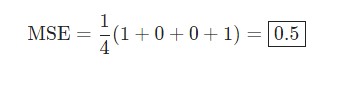
Python код среднеквадратической ошибки (MSE)

Ниже представлен код для подсчета потерь:

Python

importnumpy asnp

defmse_loss(y_true,y_pred):

# y_true и y_pred являются массивами numpy с одинаковой длиной

return((y_true-y_pred)**2).mean()

y_true=np.array([1,0,0,1])

y_pred=np.array([0,0,0,0])

print(mse_loss(y_true,y_pred))# 0.5

При возникновении сложностей с пониманием работы кода стоит ознакомиться с quickstart в NumPy для операций с массивами.

Тренировка нейронной сети — многовариантные исчисления, Часть 2

Текущая цель понятна – это минимизация потерь нейронной сети. Теперь стало ясно, что повлиять на предсказания сети можно при помощи изменения ее веса и смещения. Однако, как минимизировать потери?

В этом разделе будут затронуты многовариантные исчисления. Если вы не знакомы с данной темой, фрагменты с математическими вычислениями можно пропускать.

Для простоты давайте представим, что в наборе данных рассматривается только Alice:

Имя/Name Вес/Weight (минус 135) Рост/Height (минус 66) Пол/Gender
Alice -2 -1 1

Затем потеря среднеквадратической ошибки будет просто квадратической ошибкой для Alice:

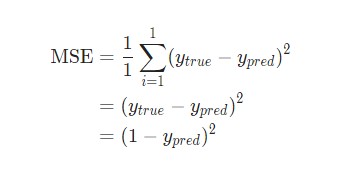
Еще один способ понимания потери – представление ее как функции веса и смещения. Давайте обозначим каждый вес и смещение в рассматриваемой сети:

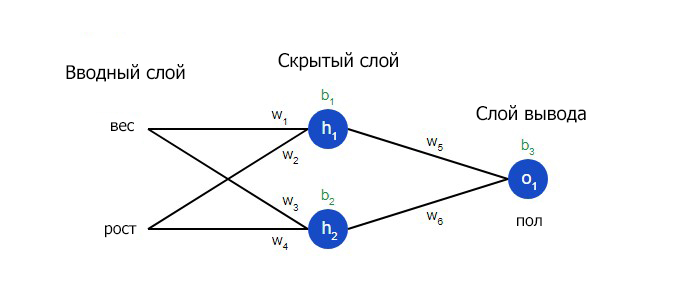
Затем можно прописать потерю как многовариантную функцию:

Представим, что нам нужно немного отредактировать w₁. В таком случае, как изменится потеря L после внесения поправок в w₁?

На этот вопрос может ответить частная производная 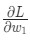. Как же ее вычислить?

Здесь математические вычисления будут намного сложнее. С первой попытки вникнуть будет непросто, но отчаиваться не стоит. Возьмите блокнот и ручку – лучше делать заметки, они помогут в будущем.

Для начала, давайте перепишем частную производную в контексте :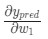

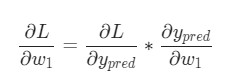
Тренировка нейронной сети Данные вычисления возможны благодаря дифференцированию сложной функции.

Подсчитать 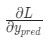можно благодаря вычисленной выше L = (1 - y_pred)²:

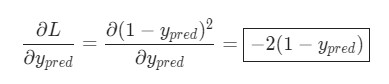
Теперь, давайте определим, что делать с 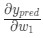. Как и ранее, позволим h₁, h₂, o₁ стать результатами вывода нейронов, которые они представляют. Дальнейшие вычисления:

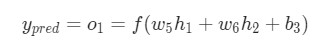
Тренировка нейронной сети и функция сигмоида

Как было указано ранее, здесь f является функцией активации сигмоида.

Так как w₁ влияет только на h₁, а не на h₂, можно записать:

Использование дифференцирования сложной функции.

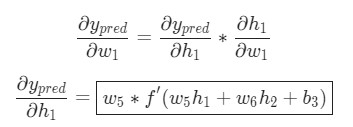
Те же самые действия проводятся для :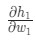

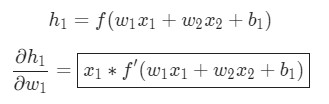
Еще одно использование дифференцирования сложной функции.

В данном случае х₁ — вес, а х₂ — рост. Здесь f?(x) как производная функции сигмоида встречается во второй раз. Попробуем вывести ее:

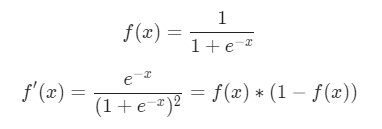
Функция f'(x) в таком виде будет использована несколько позже.

Вот и все. Теперь 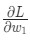разбита на несколько частей, которые будут оптимальны для подсчета:

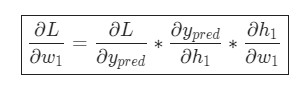
Эта система подсчета частных производных при работе в обратном порядке известна, как метод обратного распространения ошибки, или backprop.

У нас накопилось довольно много формул, в которых легко запутаться. Для лучшего понимания принципа их работы рассмотрим следующий пример.

Пример подсчета частных производных

В данном примере также будет задействована только Alice:

Имя/Name Вес/Weight (минус 135) Рост/Height (минус 66) Пол/Gender
Alice -2 -1 1

Здесь вес будет представлен как 1, а смещение как 0. Если выполним прямое распространение (feedforward) через сеть, получим:

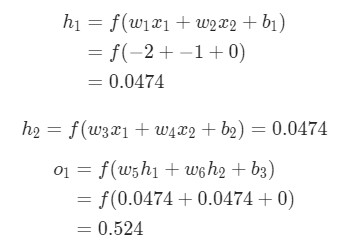
Выдачи нейронной сети y_pred = 0.524. Это дает нам слабое представление о том, рассматривается мужчина Male (0), или женщина Female (1). Давайте подсчитаем :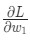

Напоминание: мы вывели f '(x) = f (x) * (1 - f (x)) ранее для нашей функции активации сигмоида.

У нас получилось! Результат говорит о том, что если мы собираемся увеличить w₁, L немного увеличивается в результате.

Тренировка нейронной сети: Стохастический градиентный спуск

У нас есть все необходимые инструменты для тренировки нейронной сети. Мы используем алгоритм оптимизации под названием стохастический градиентный спуск (SGD), который говорит нам, как именно поменять вес и смещения для минимизации потерь. По сути, это отражается в следующем уравнении:

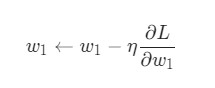
Тренировка нейронов стохастический градиентный спуск

? является константой под названием оценка обучения, что контролирует скорость обучения. Все что мы делаем, так это вычитаем 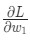из w₁:

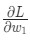
Если положительная, w₁ уменьшится, что приведет к уменьшению L.
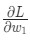
Если отрицательная, w₁ увеличится, что приведет к уменьшению L.

Если мы применим это на каждый вес и смещение в сети, потеря будет постепенно снижаться, а показатели сети сильно улучшатся.

Наш процесс тренировки будет выглядеть следующим образом:

Выбираем один пункт из нашего набора данных. Это то, что делает его стохастическим градиентным спуском. Мы обрабатываем только один пункт за раз;
Подсчитываем все частные производные потери по весу или смещению. Это может быть , и так далее;
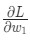
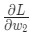
Используем уравнение обновления для обновления каждого веса и смещения;
Возвращаемся к первому пункту.

Давайте посмотрим, как это работает на практике.

Создание нейронной сети с нуля на Python

Наконец, мы реализуем готовую нейронную сеть:

Имя/Name Вес/Weight (минус 135) Рост/Height (минус 66) Пол/Gender
Alice -2 -1 1
Bob 25 6 0
Charlie 17 4 0
Diana -15 -6 1

Python

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

importnumpy asnp

defsigmoid(x):

# Функция активации sigmoid:: f(x) = 1 / (1 + e^(-x))

return1/(1+np.exp(-x))

defderiv_sigmoid(x):

# Производная от sigmoid: f'(x) = f(x) * (1 - f(x))

fx=sigmoid(x)

returnfx*(1-fx)

defmse_loss(y_true,y_pred):

# y_true и y_pred являются массивами numpy с одинаковой длиной

return((y_true-y_pred)**2).mean()

classOurNeuralNetwork:

"""

Нейронная сеть, у которой:

- 2 входа

- скрытый слой с двумя нейронами (h1, h2)

- слой вывода с одним нейроном (o1)

*** ВАЖНО ***:

Код ниже написан как простой, образовательный. НЕ оптимальный.

Настоящий код нейронной сети выглядит не так. НЕ ИСПОЛЬЗУЙТЕ этот код.

Вместо этого, прочитайте/запустите его, чтобы понять, как работает эта сеть.

"""

def__init__(self):

# Вес

self.w1=np.random.normal()

self.w2=np.random.normal()

self.w3=np.random.normal()

self.w4=np.random.normal()

self.w5=np.random.normal()

self.w6=np.random.normal()

# Смещения

self.b1=np.random.normal()

self.b2=np.random.normal()

self.b3=np.random.normal()

deffeedforward(self,x):

# x является массивом numpy с двумя элементами

h1=sigmoid(self.w1*x[0]+self.w2*x[1]+self.b1)

h2=sigmoid(self.w3*x[0]+self.w4*x[1]+self.b2)

o1=sigmoid(self.w5*h1+self.w6*h2+self.b3)

returno1

deftrain(self,data,all_y_trues):

"""

- data is a (n x 2) numpy array, n = # of samples in the dataset.

- all_y_trues is a numpy array with n elements.

Elements in all_y_trues correspond to those in data.

"""

learn_rate=0.1

epochs=1000# количество циклов во всём наборе данных

forepoch inrange(epochs):

forx,y_true inzip(data,all_y_trues):

# --- Выполняем обратную связь (нам понадобятся эти значения в дальнейшем)

sum_h1=self.w1*x[0]+self.w2*x[1]+self.b1

h1=sigmoid(sum_h1)

sum_h2=self.w3*x[0]+self.w4*x[1]+self.b2

h2=sigmoid(sum_h2)

sum_o1=self.w5*h1+self.w6*h2+self.b3

o1=sigmoid(sum_o1)

y_pred=o1

# --- Подсчет частных производных

# --- Наименование: d_L_d_w1 представляет "частично L / частично w1"

d_L_d_ypred=-2*(y_true-y_pred)

# Нейрон o1

d_ypred_d_w5=h1*deriv_sigmoid(sum_o1)

d_ypred_d_w6=h2*deriv_sigmoid(sum_o1)

d_ypred_d_b3=deriv_sigmoid(sum_o1)

d_ypred_d_h1=self.w5*deriv_sigmoid(sum_o1)

d_ypred_d_h2=self.w6*deriv_sigmoid(sum_o1)

# Нейрон h1

d_h1_d_w1=x[0]*deriv_sigmoid(sum_h1)

d_h1_d_w2=x[1]*deriv_sigmoid(sum_h1)

d_h1_d_b1=deriv_sigmoid(sum_h1)

# Нейрон h2

d_h2_d_w3=x[0]*deriv_sigmoid(sum_h2)

d_h2_d_w4=x[1]*deriv_sigmoid(sum_h2)

d_h2_d_b2=deriv_sigmoid(sum_h2)

# --- Обновляем вес и смещения

# Нейрон h1

self.w1-=learn_rate*d_L_d_ypred*d_ypred_d_h1*d_h1_d_w1

self.w2-=learn_rate*d_L_d_ypred*d_ypred_d_h1*d_h1_d_w2

self.b1-=learn_rate*d_L_d_ypred*d_ypred_d_h1*d_h1_d_b1

# Нейрон h2

self.w3-=learn_rate*d_L_d_ypred*d_ypred_d_h2*d_h2_d_w3

self.w4-=learn_rate*d_L_d_ypred*d_ypred_d_h2*d_h2_d_w4

self.b2-=learn_rate*d_L_d_ypred*d_ypred_d_h2*d_h2_d_b2

# Нейрон o1

self.w5-=learn_rate*d_L_d_ypred*d_ypred_d_w5

self.w6-=learn_rate*d_L_d_ypred*d_ypred_d_w6

self.b3-=learn_rate*d_L_d_ypred*d_ypred_d_b3

# --- Подсчитываем общую потерю в конце каждой фазы

ifepoch%10==0:

y_preds=np.apply_along_axis(self.feedforward,1,data)

loss=mse_loss(all_y_trues,y_preds)

print("Epoch %d loss: %.3f"%(epoch,loss))

# Определение набора данных

data=np.array([

[-2,-1],# Alice

[25,6],# Bob

[17,4],# Charlie

[-15,-6],# Diana

])

all_y_trues=np.array([

1,# Alice

0,# Bob

0,# Charlie

1,# Diana

])

# Тренируем нашу нейронную сеть!

network=OurNeuralNetwork()

network.train(data,all_y_trues)

Вы можете поэкспериментировать с этим кодом самостоятельно. Он также доступен на Github.

Наши потери постоянно уменьшаются по мере того, как учится нейронная сеть:

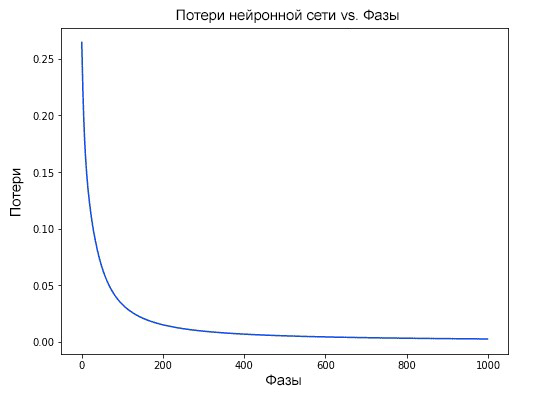
Теперь мы можем использовать нейронную сеть для предсказания полов:

Python

# Делаем предсказания

emily=np.array([-7,-3])# 128 фунтов, 63 дюйма

frank=np.array([20,2])# 155 фунтов, 68 дюймов

print("Emily: %.3f"%network.feedforward(emily))# 0.951 - F

print("Frank: %.3f"%network.feedforward(frank))# 0.039 - M

Что теперь?

У вас все получилось. Вспомним, как мы это делали:

Узнали, что такое нейроны, как создать блоки нейронных сетей;
Использовали функцию активации сигмоида в отношении нейронов;
Увидели, что по сути нейронные сети — это просто набор нейронов, связанных между собой;
Создали набор данных с параметрами вес и рост в качестве входных данных (или функций), а также использовали пол в качестве вывода (или маркера);
Узнали о функциях потерь и среднеквадратичной ошибке (MSE);
Узнали, что тренировка нейронной сети — это минимизация ее потерь;
Использовали обратное распространение для вычисления частных производных;
Использовали стохастический градиентный спуск (SGD) для тренировки нейронной сети.

Подробнее о построении нейронной сети прямого распросранения Feedforward можно ознакомиться в одной из предыдущих публикаций.

Спасибо за внимание!

Источник: python-scripts.com

Машинное обучение для начинающих: создание нейронных сетей

Комментарии: