Книга даст вам возможность глубже освоить язык Python, проверить себя на испытанных временем задачах, упражнениях и алгоритмах. Вам предстоит решать десятки заданий по программированию: от самых простых (например, найти элементы списка с помощью двоичной сортировки), до сложных (выполнить кластеризацию данных методом k-средних). Прорабатывая примеры, посвященные поиску, кластеризации, графам и пр., вы вспомните то, о чем успели позабыть, и овладеете классическими приемами решения повседневных задач.
Для кого эта книга
Эта книга предназначена для программистов среднего и высокого уровня. Опытные специалисты, которые хотят углубить свое знание Python, найдут здесь задачи, приятно знакомые со времен обучения информатике или программированию. Программисты среднего уровня познакомятся с этими классическими задачами на выбранном языке — Python. Для разработчиков, которые готовятся к собеседованию по программированию, издание, скорее всего, станет ценным подготовительным материалом.
Кроме профессиональных программистов, эту книгу могут счесть полезной студенты, обучающиеся по программам бакалавриата по информатике и интересующиеся Python. Она не претендует на роль строгого введения в структуры данных и алгоритмы. Это не учебник по структурам данных и алгоритмам. Вы не найдете на ее страницах доказательств теорем или обильного использования нотаций О большого (big-O). Напротив, эта книга позиционируется как доступное практическое руководство по методам решения задач, которые должны стать конечным продуктом изучения структуры данных, алгоритмов и классов искусственного интеллекта.
Подчеркну еще раз: предполагается, что читателям знакомы синтаксис и семантика Python. Читатель с нулевым опытом программирования едва ли извлечет пользу из этой книги, а программисту с нулевым опытом в Python наверняка будет трудно. Другими словами, «Классические задачи Computer Science на языке Python» — это книга для программистов, работающих на Python, и студентов, изучающих информатику.
Отрывок. 1.5. Ханойские башни
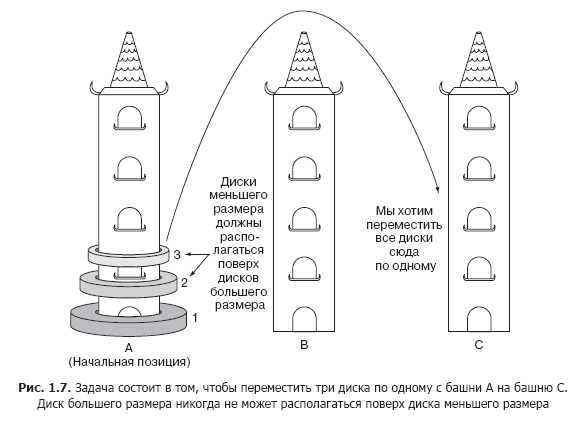
Есть три высоких вертикальных столбика (здесь и далее — башни). Мы будем их обозначать A, B и C. Диски с отверстиями в центре нанизаны на башню А. Самый широкий диск — будем называть его диском 1 — находится внизу. Остальные диски, расположенные над ним, обозначены возрастающими цифрами и постепенно сужаются кверху. Например, если бы у нас было три диска, то самый широкий из них, тот, что снизу, имел бы номер 1. Следующий по ширине диск, под номером 2, располагался бы над диском 1. Наконец, самый узкий диск, под номером 3, лежал бы на диске 2.
Наша цель — переместить все диски с башни А на башню С, учитывая следующие ограничения.
- Диски можно перемещать только по одному.
- Единственный доступный для перемещения диск — тот, что расположен наверху любой башни.
- Более широкий диск никогда не может располагаться поверх более узкого.
Схематически задача показана на рис. 1.7.
1.5.1. Моделирование башен
Стек — это структура данных, смоделированная по принципу «последним пришел — первым вышел» (last-in-first-out, LIFO). То, что попадает в стек последним, становится первым, что оттуда извлекается. Две основные операции стека — это push (поместить) и pop (извлечь). Операция push помещает новый элемент в стек, а pop удаляет из стека и возвращает последний вставленный элемент. Можно легко смоделировать стек в Python, используя список в качестве резервного хранилища (листинг 1.20).
from typing import TypeVar, Generic, List T = TypeVar('T') class Stack(Generic[T]): def __init__(self) -> None: self._container: List[T] = [] def push(self, item: T) -> None: self._container.append(item) def pop(self) -> T: return self._container.pop() def __repr__(self) -> str: return repr(self._container)В представленном классе Stack реализован метод __repr__(), позволяющий легко исследовать содержимое башни. __repr__() — это то, что будет выводиться при применении к стеку функции print().
Как говорилось во введении, в книге используются аннотации типов. Импорт Generic из модуля ввода позволяет Stack быть параметрическим классом для определенного типа в аннотациях типов. Произвольный тип T определен в T = TypeVar ('T'). Т может быть любым типом. Когда впоследствии аннотация типа будет задействоваться для Stack при решении задачи о ханойских башнях, в подсказке будет стоять Stack[int], то есть вместо T будет применен тип int. Другими словами, здесь стек — это стек целых чисел. Если вы испытываете затруднения с аннотациями типов, загляните в приложение В.
Стеки идеально подходят для задачи о ханойских башнях. Для того чтобы переместить диск на башню, мы можем использовать операцию push. Для того чтобы переместить диск с одной башни на другую, мы можем вытолкнуть его с первой (pop) и поместить на вторую (push).
Определим башни как объекты Stack и заполним первую из них дисками (листинг 1.21).
Листинг 1.21. hanoi.py (продолжение)
num_discs: int = 3 tower_a: Stack[int] = Stack() tower_b: Stack[int] = Stack() tower_c: Stack[int] = Stack() for i in range(1, num_discs + 1): tower_a.push(i)1.5.2. Решение задачи о ханойских башнях
Как можно решить задачу о ханойских башнях? Предположим, что мы пытаемся переместить только один диск. Тогда мы бы знали, как это сделать, верно? Фактически перемещение одного диска — базовый случай для рекурсивного решения данной задачи. Перемещение нескольких дисков является рекурсивным случаем. Ключевой момент в том, что у нас, по сути, есть два сценария, которые необходимо закодировать: перемещение одного диска (базовый случай) и перемещение нескольких дисков (рекурсивный случай).
Чтобы понять рекурсивный случай, рассмотрим конкретный пример. Предположим, у нас есть три диска — верхний, средний и нижний, расположенные на башне А, и мы хотим переместить их на башню С. (Впоследствии это поможет схематически описать задачу.) Сначала мы могли бы переместить верхний диск на башню С. Затем — переместить средний диск на башню B, а после этого — верхний диск с башни C на башню B. Теперь у нас есть нижний диск, все еще расположенный на башне A, и два верхних диска на башне B. По существу, мы уже успешно переместили два диска с одной башни (A) на другую (B). Перемещение нижнего диска с A на C является базовым случаем (перемещение одного диска). Теперь можем переместить два верхних диска с B на C посредством той же процедуры, что и с A на B. Перемещаем верхний диск на A, средний — на C и, наконец, верхний — с A на C.
В учебных классах информатики нередко встречаются маленькие модели этих башен, построенные из штырей и пластиковых дисков. Вы можете изготовить собственную модель с помощью трех карандашей и трех листов бумаги. Возможно, это поможет вам наглядно представить решение.
В примере с тремя дисками был простой базовый случай перемещения одного диска и рекурсивный случай перемещения остальных дисков (в данном случае двух) с применением временной третьей башни. Мы можем разбить рекурсивный случай на следующие этапы.
- Переместить верхние n – 1 дисков с башни A на башню B (временная), используя C в качестве промежуточной башни.
- Переместить нижний диск с A на C.
- Переместить n – 1 дисков с башни B на башню C, башня A — промежуточная.
Удивительно, но этот рекурсивный алгоритм работает не только для трех, а для любого количества дисков. Закодируем его как функцию hanoi(), которая отвечает за перемещение дисков с одной башни на другую, используя третью временную башню (листинг 1.22).
Листинг 1.22. hanoi.py (продолжение)
def hanoi(begin: Stack[int], end: Stack[int], temp: Stack[int], n: int) -> None: if n == 1: end.push(begin.pop()) else: hanoi(begin, temp, end, n — 1) hanoi(begin, end, temp, 1) hanoi(temp, end, begin, n - 1)После вызова hanoi() нужно проверить башни A, B и C, чтобы убедиться, что диски были успешно перемещены (листинг 1.23).
Листинг 1.23. hanoi.py (продолжение)
if __name__ == "__main__": hanoi(tower_a, tower_c, tower_b, num_discs) print(tower_a) print(tower_b) print(tower_c)Вы обнаружите, что диски действительно были перемещены. При кодировании решения задачи о ханойских башнях не обязательно понимать каждый шаг, необходимый для перемещения нескольких дисков с башни A на башню C. Мы пришли к пониманию общего рекурсивного алгоритма перемещения любого количества дисков и систематизировали его, позволяя компьютеру сделать все остальное. В этом и заключается сила формулирования рекурсивных решений задач: мы зачастую можем представлять себе решения абстрактно, не тратя силы на мысленное представление каждого отдельного действия.
Кстати, функция hanoi() будет выполняться экспоненциальное число раз в зависимости от количества дисков, что делает решение задачи даже для 64 дисков непригодным. Вы можете попробовать выполнить ее с другим числом дисков, изменяя переменную num_discs. По мере увеличения количества дисков число шагов выполнения задачи о ханойских башнях растет экспоненциально, подробнее об этом можно прочитать во множестве источников. Если интересно больше узнать о математике, стоящей за рекурсивным решением этой задачи, — см. разъяснение Карла Берча в статье «О ханойских башнях».
1.6. Реальные приложения
Различные методы, представленные в этой главе (рекурсия, мемоизация, сжатие и манипулирование на битовом уровне), настолько широко распространены в разработке современного программного обеспечения, что без них невозможно представить мир вычислений. Несмотря на то что задачи могут быть решены и без них, зачастую более логично или целесообразно решать их с использованием этих методов.
В частности, рекурсия лежит в основе не только многих алгоритмов, но даже целых языков программирования. В некоторых функциональных языках программирования, таких как Scheme и Haskell, рекурсия заменяет циклы, применяемые в императивных языках. Однако следует помнить, что все, что может быть достигнуто с помощью рекурсивного метода, может быть выполнено также итерационным способом.
Мемоизация была успешно использована для ускорения работы синтаксических анализаторов — программ, которые интерпретируют языки. Это полезно во всех задачах, где результат недавнего вычисления, скорее всего, будет запрошен снова. Еще одна область действия мемоизации — среды выполнения языков программирования. Некоторые такие среды выполнения, например для версии Prolog, автоматически сохраняют результаты вызовов функций (автомемоизация), поэтому функцию не приходится выполнять в следующий раз при таком же вызове. Это похоже на работу декоратора @lru_cache() в fib6().
Сжатие сделало мир, подключенный к Интернету с его ограниченной пропускной способностью, более терпимым. Метод битовых строк, рассмотренный в разделе 1.2, применим для простых типов данных в реальном мире, имеющих ограниченное число возможных значений, для которых даже 1 байт является избыточным. Однако большинство алгоритмов сжатия работают путем поиска шаблонов или структур в наборе данных, которые позволяют устранить повторяющуюся информацию. Они значительно сложнее, чем описано в разделе 1.2.
Одноразовые шифры не подходят для общих случаев шифрования. Они требуют, чтобы и шифратор, и дешифратор имели один из ключей (фиктивные данные в нашем примере) для восстановления исходных данных, что слишком громоздко и в большинстве схем шифрования не позволяет достичь цели — сохранить ключи в секрете. Но, возможно, вам будет интересно узнать, что название «одноразовый шифр» придумали шпионы, которые во время холодной войны использовали настоящие бумажные блокноты с записанными в них фиктивными данными для создания шифрованных сообщений.
Эти методы являются строительными блоками программ, на них основаны другие алгоритмы. В следующих главах вы увидите, как широко они применяются.
Об авторе
Дэвид Копец — старший преподаватель на кафедре компьютерных наук и инноваций в колледже Шамплейн в Берлингтоне, штат Вермонт. Он опытный разработчик программного обеспечения и автор книг Classic Computer Science Problems in Swift (Manning, 2018) и Dart for Absolute Beginners (Apress, 2014). Дэвид получил степень бакалавра экономики и степень магистра компьютерных наук в Дартмутском колледже. Вы можете связаться с ним в «Твиттере» по имени @davekopec.
» Более подробно с книгой можно ознакомиться на сайте издательства » Оглавление » Отрывок Для Хаброжителей скидка 25% по купону — Python
По факту оплаты бумажной версии книги на e-mail высылается электронная книга.
