Расчет нулевой гипотезы, на примере анализа зарплат украинских программистов
МЕНЮ
Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту
ТЕМЫ
Новости ИИ
Голосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Авторизация
2019-09-02 10:27
Этапы анализа
- Препроцессинг данных и предварительный анализ (кому интересно код тут)
- Графическое представление данных. Функция плотности распределения.
- Формулируем нулевую гипотезу (H0) (2)
- Выбираем метрику для анализа
- Используем метод bootstraping для формирования нового массива данных
- Рассчитываем p-value (3) для подтверждения или опровержения гипотезы
Препроцессинг данных
После некоторых манипуляций (код тут), приводим данные в следующий вид:
# Строка здесь это отдельный результат опроса, колонки переменные. display(data_14_1.head(), data_19_1.head()) print('Всего опрошенных программистов: {} чел. в 14 году и {} в 19 году'.format(len(data_14_1), len(data_19_1)))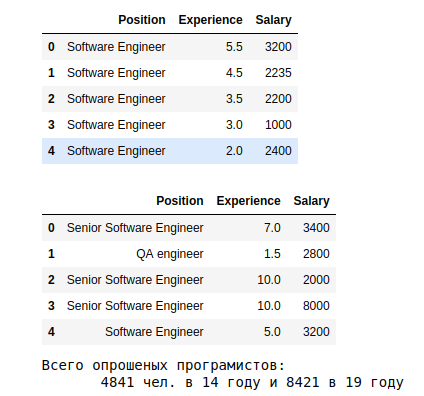
# Группируем, считаем 19 год display(pd.DataFrame(df.groupby(['Experience'])['Salary'].mean().sort_values(ascending=False)), pd.DataFrame(df.groupby(['Position'])['Salary'].mean().sort_values(ascending=False)), df.Position.value_counts())
а. По результатам видно, что в среднем в 19 году, те кто работает более 10 лет получает более 3.5к. Прослеживается зависимость стаж -> з.п.
в. Средние з.п. в 19 году, в зависимости от специализации показывают разброс в 10 раз — от 5к для System Architect, до 575 для Junior QA.
с. В последней табличке распределение по специальностям. Больше всего данных о Software Engineer, без указания уровня квалификации.
Обращаем внимание на особенности 19 года: Что-то не так с 9 годом стажа и отсутствует классификация по уровням junior, middle, senior. Можно глубже разобраться причинами outlier 9-го года. Но для данного анализа примем это как есть.
А вот с категориями — стоит разобраться. в 19 году Software Engineer 2739 человек (35% от всех) без указания уровня квалификации. Давайте посчитаем среднее и отклонения по тем, кто указал.
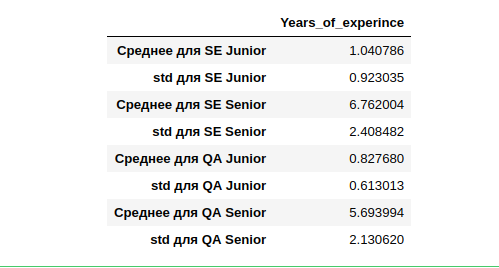
Если попытаться рассчитать Middle и использовать средний стаж у тех кто его указал, то для категоризации того кто его не указал, мы можем не верно кластеризировать всю выборку. Особенно сильно будем ошибаться на других специальностях (не SE and QA) т.е. данных слишком мало. Тем более их мало для сравнения с 14 годом.
Что можно использовать еще?
Давайте берем только уровень зарплаты как достоверный показатель уровня квалификации! (думаю будут несогласные).
Сначала строим как выглядит распределение по зарплатам для 19-го года.
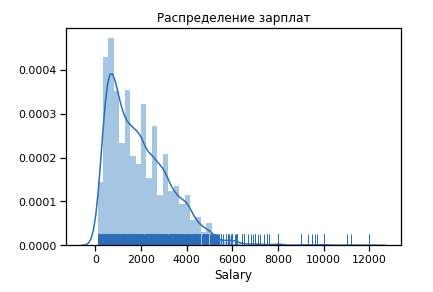
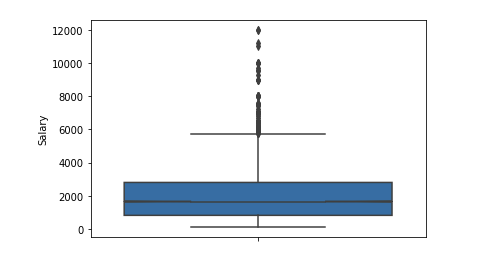
df_new = data_19_1[(data_19_1['Salary'] > 400) & (data_19_1['Salary'] < 4000)] sns.distplot(df_new['Salary'], rug=True, norm_hist=True)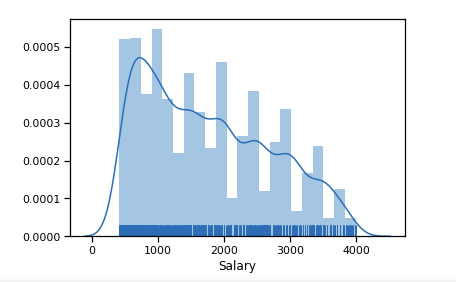
Составляем для 19 года, уровни квалификации в зависимости от зп. Range в 3600$ дает нам хороший делитель на 3 категории — 1200 $
df_new.reset_index() df_new.loc['level'] = 0 df_new.loc[df_new.Salary <= 1200, 'level'] = 'Junior' df_new.loc[(df_new.Salary > 1200) & (df_new.Salary <= 2400), 'level'] = 'Middle' df_new.loc[df_new.Salary > 2401, 'level'] = 'Senior'Рисуем — плотность распределения по категориям для 19 года.
sns.set(style="whitegrid") fig, ax = plt.subplots() fig.set_size_inches(11.7, 8.27) plt.title('Распределение зарплат по уровню квалификации в 19 году') sns.barplot(x='level', y='Salary', hue='Experience', hue_order=[1,3,5,7,10], palette='Blues', data=df_new, ci='sd')
На этом первые два этапа закончены, переходим собственно к проверки гипотез при помощи бутстрапинга.
Формулируем нулевую гипотезу (H0)
На первых этапах мы выяснили, что указанный опыт работы, не очень точно означает уровень квалификации. Тогда формируем нулевую гипотезу (ту самую которую нужно опровергнуть)
Тут много вариантов (например):
- Зависимость зарплаты от стажа в 14 году такие же как в 19-м.
- Зарплаты junior не изменились с 14 года.
Однако раз указанный стаж плохой индикатор, а расчет по отдельным категориям может запутать, то берем простой и более предметный вариант: Средний уровень зп в 14 году, такой же как в 19 году это наша нулевая гипотеза H0 (2).
То есть предполагаем, что зарплаты за 5 лет не изменились.
НЕ верность гипотезы, несмотря на всю ее очевидность, мы сможем точно проверить рассчитав P-value для нулевой гипотезы.
# Считаем среднии зп по всей выборке (14 и 19 года), рассчитываем доверительный интервал 95 % mean_salary_14 = np.mean(data_14_1['Salary']) conf_salary_14 = np.percentile(data_14_1['Salary'], [2.5, 97.5]) mean_salary_19 = np.mean(data_19_1['Salary']) conf_salary_19 = np.percentile(data_19_1['Salary'], [2.5, 97.5]) diff_mean_salary = mean_salary_19 - mean_salary_14 Средняя зп в 14 году 1797$, где доверительный интервал 95% [300.0 4000.0]
Средняя зп в 19 году 1949$, где доверительный интервал 95% [300.0 5000.0]
Разница в средних зарплатах в 14 и 19 году: 152$
Метрика для анализа
Логично выбрать именно средние значения в качестве нашей метрики. Возможны и другие варианты, например медиана, что часто делают в случае значительного количества outliers. Однако средняя как оценка проста в понимании и тоже неплохо даст необходимое представление.
Пишем bootstrapping функцию.
# Функция для bootstraping def bootstrap(data, func): boots = np.random.choice(data, len(data)) return func(boots) def bootstrapping(data, func=np.mean, size=1): reps = np.empty(size) for i in range(size): reps[i] = bootstrap(data, func) return repsРассчитываем нашу статистику.
# Объединяем 14 и 19 года вместе - что бы создать перемешанный массив данных data = np.concatenate((data_14_1['Salary'].values, data_19_1['Salary'].values)) # Считаем среднее значение за 2 года data_mean = np.mean(data) # Создаем измененные массивы данных за 14 и 19 года, от значения зп отнимаем среднее и добавляем среднее обьеденненого массива data_14_shifted = data_14_1['Salary'].values - np.mean(data_14_1['Salary'].values) + data_mean data_19_shifted = data_19_1['Salary'].values - np.mean(data_19_1['Salary'].values) + data_mean # Генерируем 10000 копий массивов используя нашу функцию, выбранную метрику data_14_bootsted = bootstrapping(data_14_shifted, np.mean, size=10000) data_19_bootsted = bootstrapping(data_19_shifted, np.mean, size=10000) # Считаем разницу в средних в сгенерированных массивах. Что бы знать с чем сравнивать. mean_diff = data_19_bootsted - data_14_bootsted # Рассчитываем P value как доля суммы средних нашей сгенерированной через бутстрапинг выборки со средними к размеры самой выборки. p_value = sum(mean_diff >= diff_mean_salary) / len(mean_diff) print('p-value = {}'.format(p_value))p-value = 0.0
Значения p-value до 0,05 считаются незначительными, а в нашем случае оно равно = 0. Что означает, нулевая гипотеза опровергнута — средние значения зарплат в 14 году и 19 году разные и это не случайный результат или значительное количество outliers.
Сгенерированные нами 10 тыс подобных массивов, в среднем не смогли получить в сумме большей таких ототожнений, чем непосредственно сами данные.
Хотя мы потратили много внимания на первые два этапа, мы сформулировали правильную гипотезу и выбрали верную метрику. В более сложных задачах, с большим количеством переменных, без таких предварительных этапов, аналитика может привести к неверной интерпретации. Не стоит их пропускать.
В результате нашего исследования уровня зарплат за 14 и 19 года, мы пришли к следующим выводам:
- Исходя из данных опроса, указанный стаж не совсем подходящий критерий для определения уровня зарплат и квалификации.
- Разделение на уровень квалификации точнее всего будет проводиться на основании уровня зарплат.
- Зарплаты программистов с 14 года по 19 выросли (в среднем на 8.5%) и это не случайный результат.
Спасибо за Ваше внимание. Буду рад комментариям и критике.
Источники
Источник: habr.com