Эволюционирующие клеточные автоматы
МЕНЮ
Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту
ТЕМЫ
Новости ИИ
Голосовой помощник
Городские сумасшедшие
ИИ в медицине
ИИ проекты
Искусственные нейросети
Слежка за людьми
Угроза ИИ
Компьютерные науки
Машинное обуч. (Ошибки)
Машинное обучение
Машинный перевод
Реализация ИИ
Реализация нейросетей
Создание беспилотных авто
Трезво про ИИ
Философия ИИ
Генетические алгоритмы
Капсульные нейросети
Основы нейронных сетей
Распознавание лиц
Распознавание образов
Распознавание речи
Техническое зрение
Чат-боты
Авторизация
2019-09-26 04:40

Соединим клеточные автоматы с генетическим алгоритмом и посмотрим, что из этого получится. В статье присутствуют Gif (трафик!) и контрастные картинки. У эпилептиков может случиться эпилептический припадок.
Правила для клеточных автоматов.
Самый простой клеточный автомат — одномерный клеточный автомат (существуют также нульмерные — о них поговорим ниже). В одномерном клеточном автомате у нас есть одномерный массив, ячейки которого (клетки) могут принимать одно из двух состояний (1/0, true/false, белая/черная, живая/мертвая). Следующее состояние клетки в массиве определяется текущим состоянием клетки и состоянием двух соседних клеток, по некоторому правилу.
Всего существует комбинаций состояний клетки и двух соседних клеток:

Далее для каждой из комбинаций запишем состояние клетки для следующей итерации (для следующего состояния автомата):
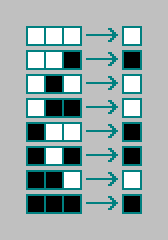
Получили правило для клеточного автомата. Правила для одномерных клеточных автоматов кодируются 8 битами («код Вольфрама»). Всего существует элементарных клеточных автоматов:
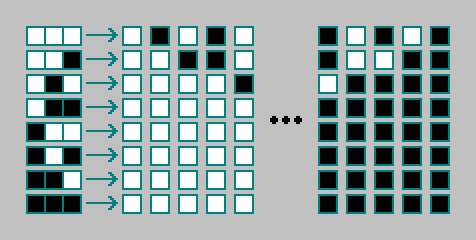
 Для удобства запишем клетки в строку (выбранный порядок будем использовать далее в статье):
Для удобства запишем клетки в строку (выбранный порядок будем использовать далее в статье):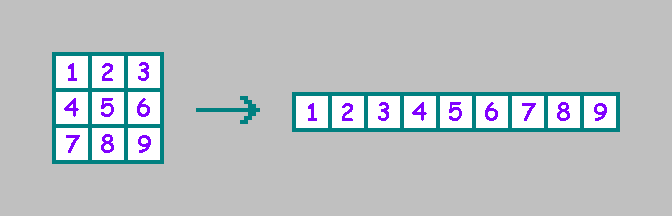
Для двухмерного клеточного автомата существует комбинаций состояний клетки и 8-ми соседних клеток:

Правило для двухмерного клеточного автомата кодируется 512 битами. Всего существует двухмерных клеточных автоматов:
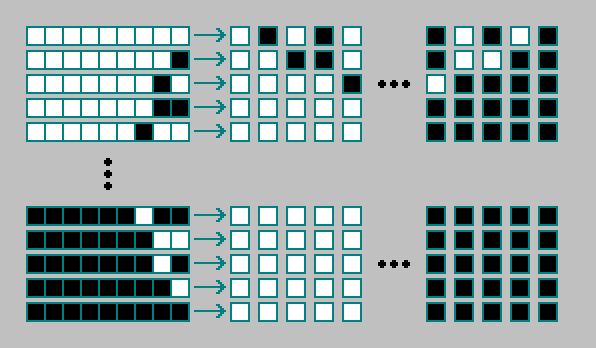
Вручную такое количество автоматов не перебрать. Если бы мы каждую секунду просматривали по одному автомату — за время существования Вселенной мы бы успели просмотреть всего автоматов.
Простой перебор не работает, но с помощью генетического алгоритма мы можем найти автоматы, которые наилучшим образом соответствуют некоторым заранее заданным критериям.
Программировать будем на JavaScript. Все фрагменты кода спрятаны под спойлеры, чтобы не смущать читателей, не знакомых с языками программирования.
Двухмерный клеточный автомат.
Напишем двухмерный клеточный автомат с случайным правилом. Правило будем хранить в массиве rule, длина которого rulesize=512:
Заполняем массив rule
var rulesize=512; var rule=[]; for(var i=0;i<rulesize;i++) rule[i]=Math.round(Math.random());Заполняем начальное состояние автомата
var sizex=89; var sizey=89; var size=2; var a=[]; for(var x=0;x<sizex;x++){ a[x]=[] for(var y=0;y<sizey;y++){ a[x][y]=Math.round(Math.random()); if(a[x][y]) context.fillRect(x*size, y*size, 1*size, 1*size); } }Функция, вычисляющая следующее состояние автомата, выглядит следующим образом (чтобы не захламлять — убрал инициализацию холста):
Считаем следующее состояние автомата
function countpoints(){ var temp=[]; var xm, xp, ym, yp, q; for(var x=0;x<sizex;x++){ xm=x-1; if(xm==-1) xm=sizex-1; xp=x+1; if(xp==sizex) xp=0; temp[x]=[]; for(var y=0;y<sizey;y++){ ym=y-1; if(ym==-1) ym=sizey-1; yp=y+1; if(yp==sizey) yp=0; q=''+a[xm][ym]+a[x][ym]+a[xp][ym]+a[xm][y]+a[x][y]+a[xp][y]+a[xm][yp]+a[x][yp]+a[xp][yp]; q=parseInt(q, 2); temp[x][y]=rule[q]; if(temp[x][y]) context.fillRect(x*size, y*size, 1*size, 1*size); } } a=temp; }Поле автомата свернуто в бублик
xm=x-1; if(xm==-1) xm=sizex-1; xp=x+1; if(xp==sizex) xp=0;... далее
q=''+a[xm][ym]+a[x][ym]+a[xp][ym]+a[xm][y]+a[x][y]+a[xp][y]+a[xm][yp]+a[x][yp]+a[xp][yp]; q=parseInt(q, 2); temp[x][y]=rule[q];Оптимизированный вариант
q=a[xm][ym]; q=(q<<1)+a[x][ym]; q=(q<<1)+a[xp][ym]; q=(q<<1)+a[xm][y]; q=(q<<1)+a[x][y]; q=(q<<1)+a[xp][y]; q=(q<<1)+a[xm][yp]; q=(q<<1)+a[x][yp]; q=(q<<1)+a[xp][yp]; temp[x][y]=rule[q];заменяем предыдущее состояние новым
a=temp;setInterval
timerId = setInterval(function() { countpoints(); }, 1); Далее перейдем к настройке нашего «телевизора» с помощью генетического алгоритма.
Далее перейдем к настройке нашего «телевизора» с помощью генетического алгоритма.Генетический алгоритм.
Размер начальной популяции — 200 автоматов (особей). Для правил, вместо одномерного массива rule будем использовать двухмерный массив population. Первый индекс (n) — номер особи в популяции.
Создаем популяцию
var PopulationSize=200; var rulesize=512; var population=[]; var fitness=[]; for(var n=0;n<PopulationSize;n++){ population[n]=[]; fitness[n]=0; for(var i=0;i<rulesize;i++){ population[n][i]=Math.round(Math.random()); } }Эволюционный процесс.
Из нашей популяции берем половину наиболее приспособленных (по коэффициенту fitness) особей. Оставшуюся половину уничтожаем. Далее берем по две выжившие особи и скрещиваем их.

Функция evolute();
function evolute(){ var sizehalf=PopulationSize/2; var sizequarter=sizehalf/2; var arrayt=[]; for(var n=0; n<PopulationSize; n++) arrayt[n]=[population[n], fitness[n]]; arrayt.sort(sortf); arrayt.length=sizehalf; population=[]; fitness=[]; for(var i=0; i<sizequarter; i++){ var i0=i*4; var i1=i*4+1; var i2=i*4+2; var i3=i*4+3; var removed1=Math.floor(Math.random()*(arrayt.length)); var parent1f = arrayt.splice(removed1,1); var parent1=parent1f[0][0]; var removed2=Math.floor(Math.random()*(arrayt.length)); var parent2f = arrayt.splice(removed2,1); var parent2=parent2f[0][0]; var child1=[]; var child2=[]; var qen=Math.floor(Math.random()*rulesize); var temp0=parent1; var temp1=parent2; var temp2=temp0.splice(qen,rulesize); var temp3=temp1.splice(qen,rulesize); var parent1=temp0.concat(temp2); var parent2=temp1.concat(temp3); var child1=temp1.concat(temp2); var child2=temp0.concat(temp3); population[i0]=parent1; population[i1]=parent2; population[i2]=child1; population[i3]=child2; fitness[i0]=0; fitness[i1]=0; fitness[i2]=0; fitness[i3]=0; } var mutation=document.getElementById("mutatepercent").value*1; var m=100/mutation; var m2=0;//0 for(var i=0; i<PopulationSize; i++){ var rnd=Math.floor(Math.random()*(m))+1; if(rnd==1){ var rnd2=Math.floor(Math.random()*(m2))+1; for(var j=0;j<rnd2;j++){ var gen=Math.floor(Math.random()*(rulesize)); if(population[i][gen]) population[i][gen]=0; else population[i][gen]=1; } } } }Естественный отбор.
Перед запуском эволюционного процесса надо произвести отбор. Отбор может быть как естественным, так и искусственным. Искусственный отбор производится вручную — о нем чуть позже. Для естественного отбора мы зададим некоторые критерии и будем отбирать автоматы, которые наилучшим образом соответствуют заданным критериям.
Какие критерии можно определить заранее? Возьмем самый простой. Наш «телевизор» слишком сильно мигает. Сохраним два состояния клеточного автомата — на 99 и на 100 итерациях. Посчитаем количество клеток, которые не изменились. Полученное число будем использовать в качестве коэффициента приспособленности. Очевидно, что одного критерия нам не хватит. Легко вручную подобрать автомат, который будем наилучшим образом соответствовать заданному критерию: автомат [0,0,0,...,0] и автомат [1,1,1,...,1]. Эти два автомата на первой итерации заполняются нулями или единицами и перестают изменять свое состояние. Определим второй критерий: разница между количеством 0 и 1 (клеток) в автомате не превышает 100 (число взято «от балды»).
array1 — состояние автомата на 99-й итерации. array2 — на 100-й итерации:
Считаем
function countfitness(array1, array2){ var sum=0; var a0=0; var a1=0; for(var x=0;x<sizex;x++){ for(var y=0;y<sizey;y++){ if(array1[x][y]==array2[x][y]) sum++; if(array1[x][y]==0){ a0++; }else{ a1++; } } } if(Math.abs(a0-a1)<100) return sum; return 0; }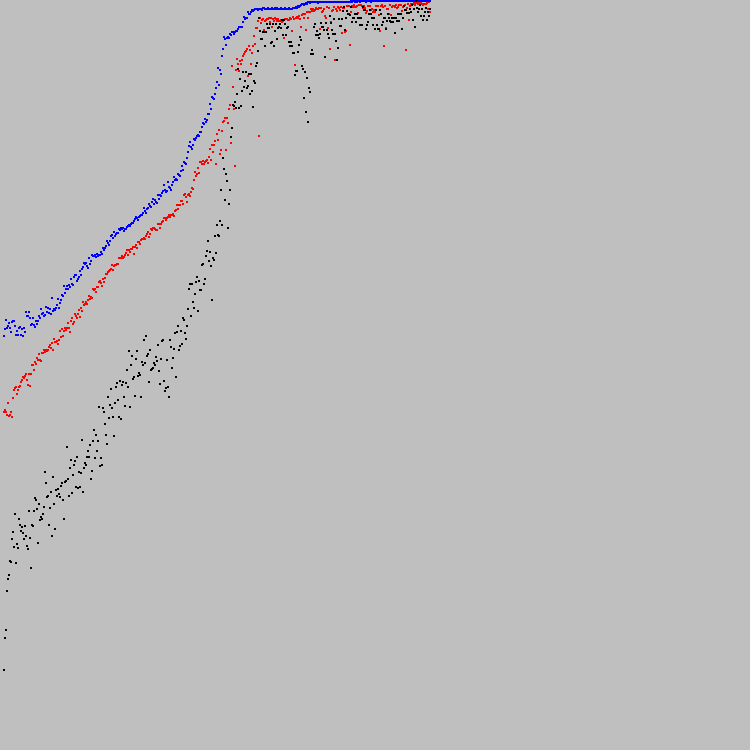

 Изменим критерии отбора.
Изменим критерии отбора.Будем считать количество клеток, для которых в окрестности Мура порядка 2 появляется некоторый паттерн. Паттерн возьмем самый простой:
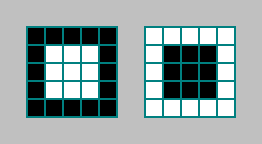 Этот критерий интересен тем, что мы проверяем 25 клеток, в то время, как автомат вычисляет состояние клетки исходя из состояний 9 клеток.
Этот критерий интересен тем, что мы проверяем 25 клеток, в то время, как автомат вычисляет состояние клетки исходя из состояний 9 клеток.Критерий очень жесткий. Если взять случайный автомат, после 100 итераций он выглядит так:
 Ни одна клетка в таком автомате не соответствует заданному критерию. Поэтому немного смягчим критерий:
Ни одна клетка в таком автомате не соответствует заданному критерию. Поэтому немного смягчим критерий:1. Разрешим сделать одну ошибку в паттерне.
2. Паттерн будем искать не на последней итерации, а на последних 50 итерациях.
Второй критерий (баланс между белыми и черными) уберем.
Запускаем. График:


 Генофонд (3569):
Генофонд (3569):

На картинке ниже можно посмотреть, как формируется осциллятор (глайдер) в этом автомате:
 Мы можем запустить автомат с начальным состоянием, в котором заполнена одна клетка. Далее зафиксировать все комбинации клеток, встречающиеся на следующих итерациях автомата. Массив генов (генотип автомата) — массив всех возможных комбинаций. Выделив из них только встречающиеся комбинации, мы можем легко отметить все гены, которые участвуют в формировании осциллятора. Серые полосы — гены, которые не участвуют в формировании осциллятора:
Мы можем запустить автомат с начальным состоянием, в котором заполнена одна клетка. Далее зафиксировать все комбинации клеток, встречающиеся на следующих итерациях автомата. Массив генов (генотип автомата) — массив всех возможных комбинаций. Выделив из них только встречающиеся комбинации, мы можем легко отметить все гены, которые участвуют в формировании осциллятора. Серые полосы — гены, которые не участвуют в формировании осциллятора:


Последняя (100) итерация:

Немного не тот результат, которого мы ожидали. Черные квадраты есть, белых — нет. Ужесточим второй критерий: разница между количеством белых и черных клеток не превышает 100.
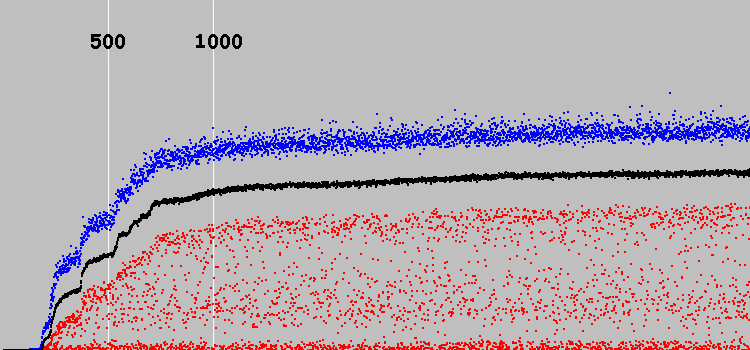
Запускаем 14865 циклов эволюции.
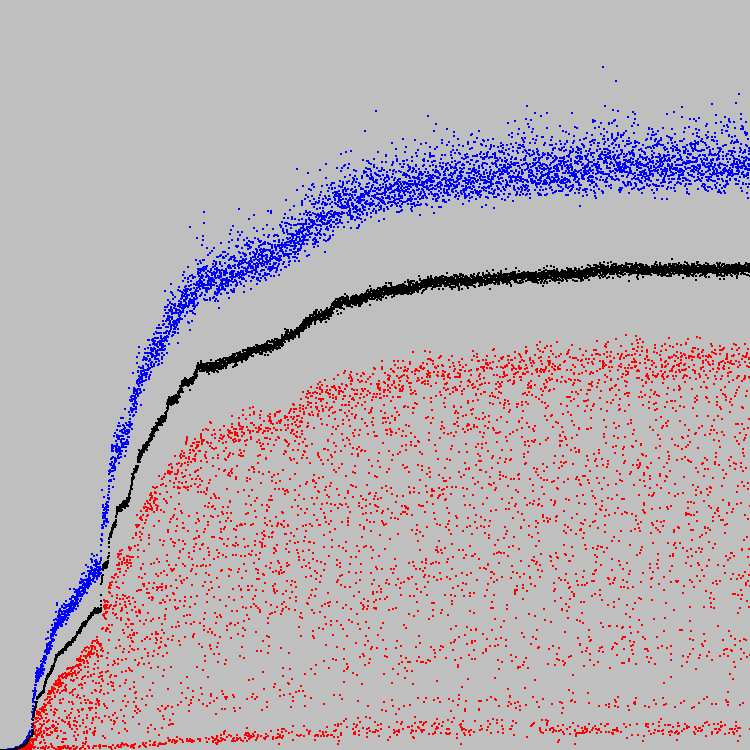
На графике сравнение средних коэффициентов приспособленности популяций. Синие точки — наш автомат. Белые и черные — предыдущие автоматы.

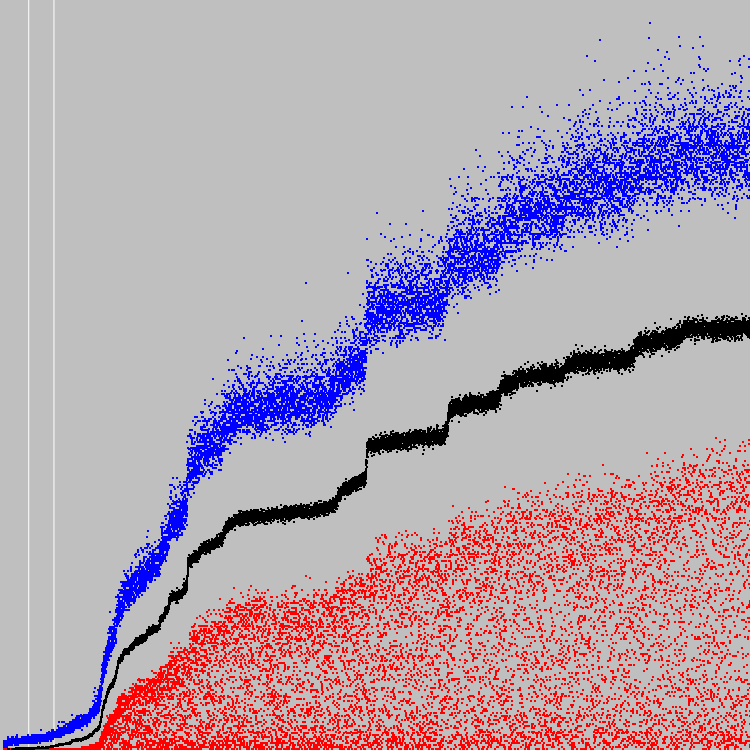
 Последняя (50) итерация:
Последняя (50) итерация: Приемлемый результат не найден. Второй критерий усложняет поиск, поэтому от него откажемся (далее в статье не используем). Оставим этот паттерн и поищем еще несколько других паттернов.
Приемлемый результат не найден. Второй критерий усложняет поиск, поэтому от него откажемся (далее в статье не используем). Оставим этот паттерн и поищем еще несколько других паттернов.Паттерн:
 Запускаем. 3000 циклов эволюции. График:
Запускаем. 3000 циклов эволюции. График: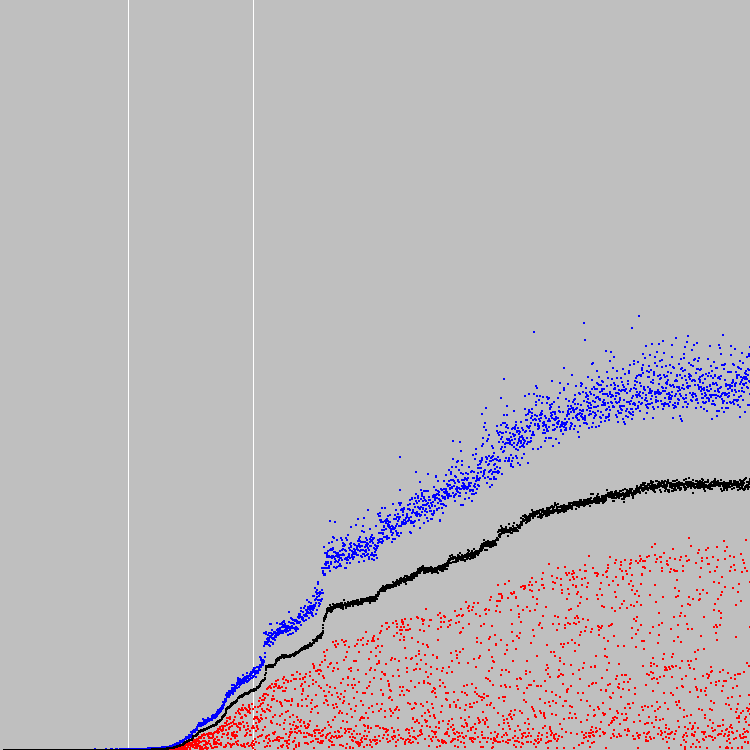

 Последняя (100) итерация:
Последняя (100) итерация: Паттерн:
Паттерн:
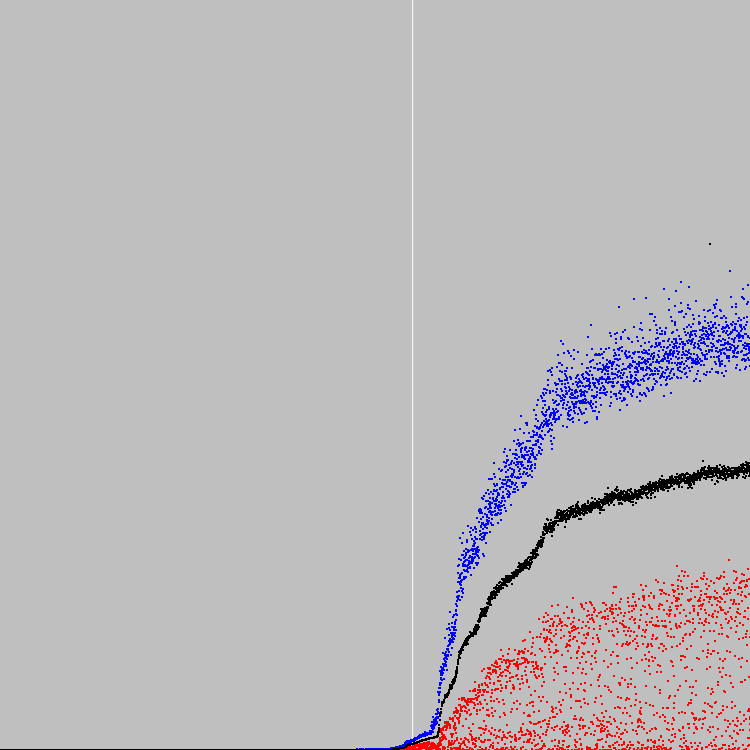
 На Gif 100 итераций. Еще после некоторого числа итераций (около 500-2000) состояние автомата практически полностью упорядочено (высота и ширина автомата специально выбраны нечетными числами, чтобы автомат не мог упорядочиться полностью):
На Gif 100 итераций. Еще после некоторого числа итераций (около 500-2000) состояние автомата практически полностью упорядочено (высота и ширина автомата специально выбраны нечетными числами, чтобы автомат не мог упорядочиться полностью): Автомат с четными размерами сторон, после некоторого числа итераций принимает полностью упорядоченное состояние. Автомат 90х90, примерно 1200 итераций:
Автомат с четными размерами сторон, после некоторого числа итераций принимает полностью упорядоченное состояние. Автомат 90х90, примерно 1200 итераций: Промежуточное решение (найденное на 2500-ом цикле эволюции):
Промежуточное решение (найденное на 2500-ом цикле эволюции): Данный автомат тоже умеет перерабатывать некоторое начальное хаотическое состояние в некоторое конечное упорядоченное (конечное упорядоченное состояние — смещение паттерна по оси Х влево + несколько клеток-осцилляторов).
Данный автомат тоже умеет перерабатывать некоторое начальное хаотическое состояние в некоторое конечное упорядоченное (конечное упорядоченное состояние — смещение паттерна по оси Х влево + несколько клеток-осцилляторов).Автомат 16х16 упорядочился примерно за 100 итераций:
 64х64 — около 6000 итераций:
64х64 — около 6000 итераций: 90х90 — около 370000 итераций:
90х90 — около 370000 итераций: 11х11 (нечетные размеры поля автомата) — около 178700 итераций:
11х11 (нечетные размеры поля автомата) — около 178700 итераций:На картинке ниже, автомат на поле 256x256 на 100000-й итерации:



 Еще один паттерн:
Еще один паттерн: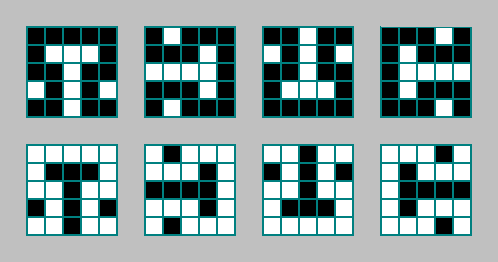

 Упорядоченное состояние автомата (смещение паттерна вверх по оси Y + несколько клеток-осцилляторов):
Упорядоченное состояние автомата (смещение паттерна вверх по оси Y + несколько клеток-осцилляторов): Гораздо интересней наблюдать не за самим автоматом, а за мутантами, появляющимися в этой популяции:
Гораздо интересней наблюдать не за самим автоматом, а за мутантами, появляющимися в этой популяции:
Следующий паттерн:

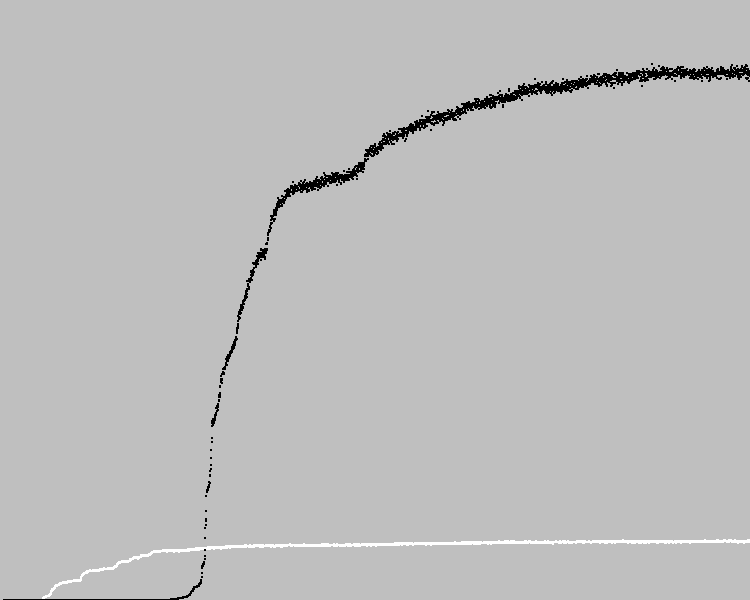
 Для искомого паттерна, на 100-й итерации каждого автомата в популяции, в окружении каждой клетки будем считать количество клеток совпадающих с паттерном. Будем брать только наилучший результат для каждого автомата. Количество клеток, совпавших с паттерном, будем использовать в качестве коэффициента приспособленности. Паттерн состоит из 7х17=119 клеток. Это число будем считать оптимальным решением. 6000 циклов эволюции позволили найти автомат, рисующий паттерн с 5-ю ошибками (114 клеток совпадают с паттерном).
Для искомого паттерна, на 100-й итерации каждого автомата в популяции, в окружении каждой клетки будем считать количество клеток совпадающих с паттерном. Будем брать только наилучший результат для каждого автомата. Количество клеток, совпавших с паттерном, будем использовать в качестве коэффициента приспособленности. Паттерн состоит из 7х17=119 клеток. Это число будем считать оптимальным решением. 6000 циклов эволюции позволили найти автомат, рисующий паттерн с 5-ю ошибками (114 клеток совпадают с паттерном).График в произвольном масштабе:
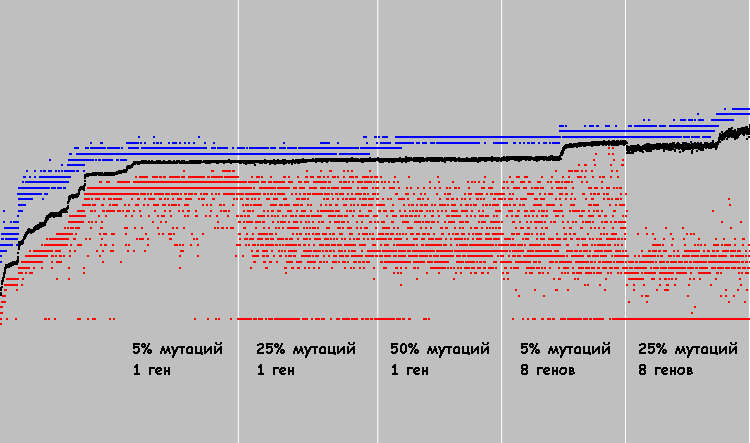

 Лучший автомат на 100-й итерации:
Лучший автомат на 100-й итерации: Искомый и найденный паттерны:
Искомый и найденный паттерны:

 Искомый и найденный паттерны:
Искомый и найденный паттерны:

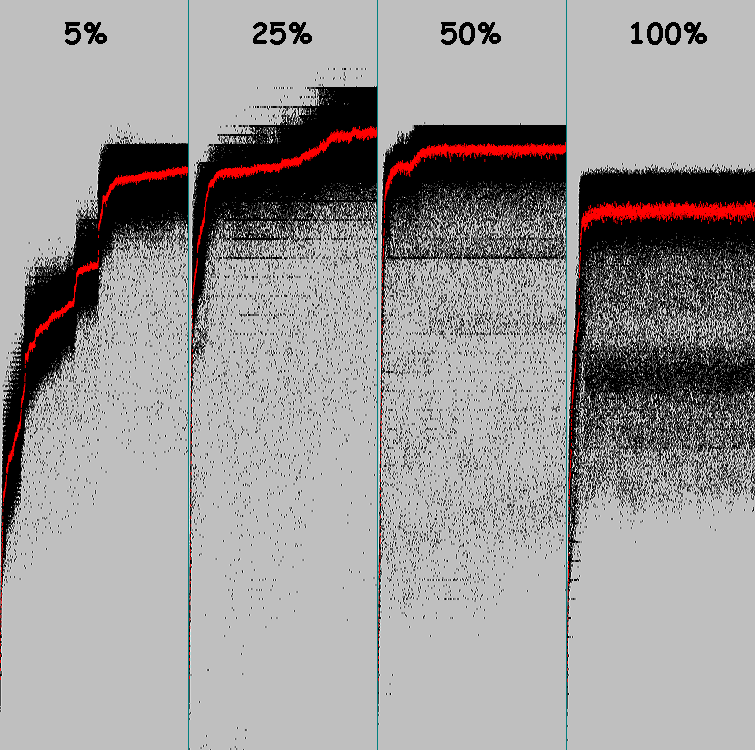












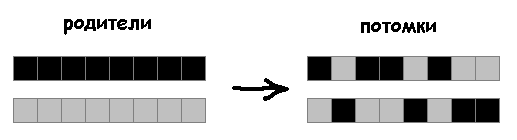


Second-order cellular automaton
Рассмотрим нульмерный клеточный автомат первого порядка (все клеточные автоматы, которые мы рассматривали выше — первого порядка). Нульмерный клеточный автомат состоит из одной клетки. Клетка может находиться в одном из двух состояний. Следующее состояние клетки (t) определяется текущим состоянием клетки (t-1). Всего существует 4 нульмерных клеточных автомата (среди них один осциллятор):
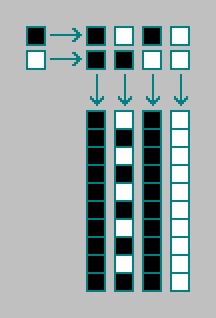 В клеточном автомате второго порядка, следующее состояние клетки (t) определяется текущим состоянием (t-1) и предыдущим состоянием клетки (t-2). Всего существует 4 комбинации двух состояний клетки. — количество нульмерных клеточных автоматов второго порядка:
В клеточном автомате второго порядка, следующее состояние клетки (t) определяется текущим состоянием (t-1) и предыдущим состоянием клетки (t-2). Всего существует 4 комбинации двух состояний клетки. — количество нульмерных клеточных автоматов второго порядка:


Поиск клеточного автомата -го порядка с периодом осцилляции равным — задача нетривиальная и крайне интересная. Эта тема заслуживает отдельной статьи.
В одномерных клеточных автоматах второго порядка, следующее состояние клетки определяется текущим состоянием трех клеток и предыдущим состоянием одной клетки:
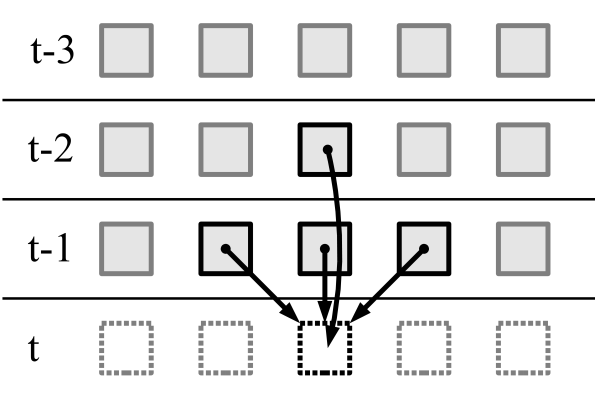
Код:
Одномерный клеточный автомат второго порядка
var rule=[]; for(var i=0;i<16;i++) rule[i]=Math.round(Math.random()); var a=[]; var b=[]; var temp; for(var x=0;x<sizex;x++){ a[x]=0; b[x]=0; } b[63]=1; var xm, xp, q; for(var y=2;y<sizey;y++){ temp=[]; for(var x=0;x<sizex;x++){ xm=x-1; if(xm<0) xm=sizex+xm; xp=x+1; if(xp>=sizex) xp=xp-sizex; q=b[xm]; q=(q<<1)+b[x]; q=(q<<1)+b[xp]; q=(q<<1)+a[x]; temp[x]=rule[q]; if(temp[x]) context.fillRect(x*size, y*size, size, size); } a=b; b=temp; }0011111011001000:






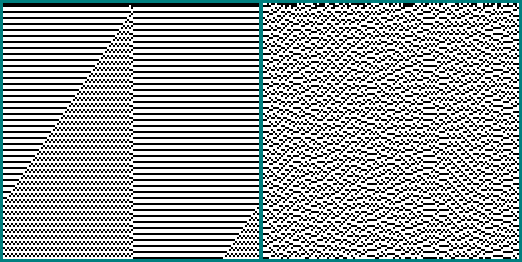



Искусственный отбор
Подобно одномерному клеточному автомату второго порядка, в двухмерном клеточном автомате второго порядка будем использовать дополнительную клетку из предыдущего (t-2) состояния автомата.
Для удобства эту клетку разместим в начале двоичной строки:
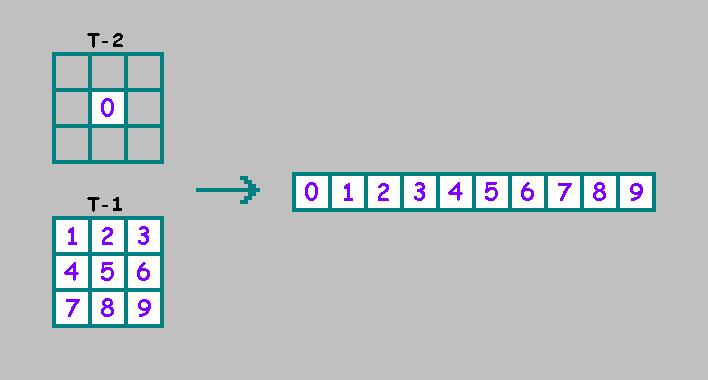
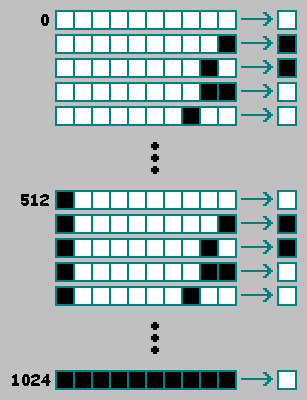
— количество существующих двухмерных автоматов второго порядка.
Для естественного отбора мы определяли некоторый критерий и сравнивали автоматы по этому критерию. В процессе искусственного отбора, мы выбираем автоматы вручную, пользуясь некоторым невнятным принципом: «этот автомат интересный, а тот — не очень».
Данный принцип не позволяет выбирать лучший автомат среди случайных автоматов:



 Существует несколько способов решить эту проблему. Предлагаю рассмотреть четыре способа.
Существует несколько способов решить эту проблему. Предлагаю рассмотреть четыре способа.1. В начальном состоянии автомата заполнена одна клетка
Один из способов — наблюдать за развитием клеточного автомата, в начальном состоянии которого заполнена одна клетка.
Заполняем начальную популяцию случайными автоматами. Несколько автоматов из начальной популяции (30 итераций для каждого):

![]()








2. Генотип заполнен частично
Если нарушить соотношение единиц и нулей в генотипе — нарушится соотношение единиц и нулей в фенотипе.
В генотипе (правиле) автомата записаны следующие состояния клетки для всех возможных комбинаций клетки и соседних клеток. Если в генотипе больше нулей (или единиц) — в следующих состояниях автомата накапливаются нули (или единицы). Любопытно посмотреть на корреляционную зависимость между соотношением единиц и нулей в генотипе и соотношением единиц и нулей в фенотипе.
Построим график.
Создадим популяцию из 200 автоматов. Генотипы заполняем нулями (1024 гена в генотипе двухмерного автомата второго порядка). Далее генов заполняем единицами. Для первой популяции , для 513-й популяции . По оси — номер популяции. По оси отмечаем (белыми точками) соотношение единиц и нулей в генофонде популяции. Получили гиперболу:
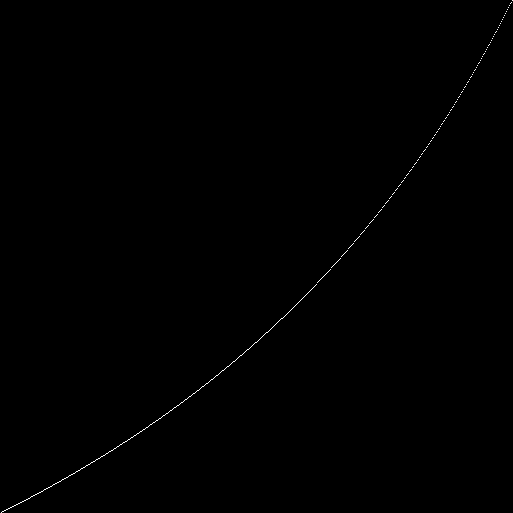
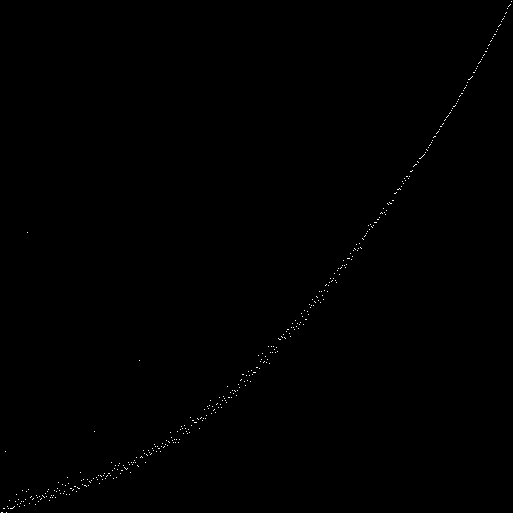













 Автомат постепенно заполняет популяцию.
Автомат постепенно заполняет популяцию.После восьмого отбора:

 Популяция после тринадцати отборов:
Популяция после тринадцати отборов:
 Посмотреть в динамике.
Посмотреть в динамике.  Посмотреть в динамике.
Посмотреть в динамике.  Посмотреть в динамике.
Посмотреть в динамике.  Посмотреть в динамике.
Посмотреть в динамике.  Посмотреть в динамике.
Посмотреть в динамике.  Посмотреть в динамике.
Посмотреть в динамике.  Посмотреть в динамике.
Посмотреть в динамике.  Посмотреть в динамике.
Посмотреть в динамике.  Посмотреть в динамике.
Посмотреть в динамике.  Посмотреть в динамике.
Посмотреть в динамике. 3. Автомат Конвея и ему подобные
Самый известный двухмерный клеточный автомат первого порядка — автомат Конвея Игра «Жизнь». Правила для автомата Конвея записываются следующим образом: Если вокруг мертвой клетки 3 живые клетки — клетка оживает (в противном случае остается мертвой). Если вокруг живой клетки 2 или 3 живые клетки — клетка остается живой (в противном случае умирает). Мертвая клетка — 0, живая клетка — 1. Вокруг клетки может быть от 0 до 8 живых клеток. По 9 вариантов вокруг живой и вокруг мертвой клетки. Запишем все варианты в массив r:
массив r
r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ];Расписываем правило
r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ]; var rule=[]; var q1, q2; for(var i=0;i<512;i++){ var ii=i.toString(2); for(var j=ii.length;j<9;j++) ii='0'+ii; q1=1*ii[4]; q2=1*ii[0]+1*ii[1]+1*ii[2]+1*ii[3]+1*ii[5]+1*ii[6]+1*ii[7]+1*ii[8]; if(q1==0) rule[i]=r[q2]; else rule[i]=r[q2+9]; }Оптимизированный вариант
r=[ 0,0,0,1,0,0,0,0,0, 0,0,1,1,0,0,0,0,0 ]; var rule=[]; for(var i=0;i<512;i++){ var q=((i>>4)&1)*8; for(var j=0;j<9;j++){ q+=(i>>j)&1; } rule[i]=r[q]; }Копируем
for(var i=0;i<512;i++){ if(rule[i]==0) rule[i+512]=0; else rule[i+512]=1; }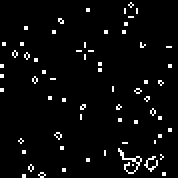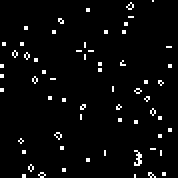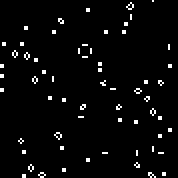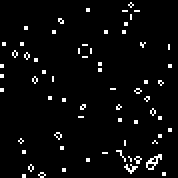 Массив r состоит из 18 ячеек. Существует автоматов подобных автомату Конвея (которые можно записать теми же правилами: количество живых клеток в окружении мертвой, при которых клетка оживает и количество живых клеток в окружении живой, при которых клетка умирает).
Массив r состоит из 18 ячеек. Существует автоматов подобных автомату Конвея (которые можно записать теми же правилами: количество живых клеток в окружении мертвой, при которых клетка оживает и количество живых клеток в окружении живой, при которых клетка умирает).Посмотреть на них можно здесь (по умолчанию запускается автомат Конвея, кнопка «Change rule» заполняет массив r случайным образом). Несколько случайных автоматов (двоичный код — массив r): 110010011001111111

100001100110111110

011111000100101110

010000110000110010

001111010011100111

000111001000000110

000101100010100001
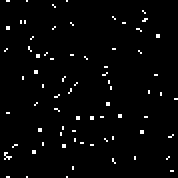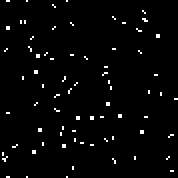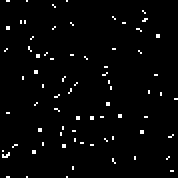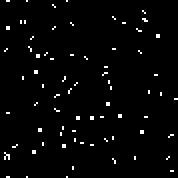
000001111101011111

000001100110111111

Для генетического алгоритма, в качестве генотипа, можно использовать, как массив r ( комбинаций), так и массив rule ( комбинаций для клеточного автомата первого порядка и — для клеточного автомата второго порядка).
— сравнительно небольшое число. Это число позволяет подобрать правило для автомата вручную, без использования генетического алгоритма (собственно, что и сделал Конвей).
Если же заполнить массив rule случайными автоматами этого типа и использовать этот массив в качестве генотипа — тогда эксперимент можно считать неудачным, в некоторой степени (в достаточной, чтобы не показывать в статье результаты этого эксперимента). В правилах клеточных автоматов этого типа присутствует симметрия. Например, для следующих комбинаций клеток:







 После первого отбора избавились от автоматов, которые не развиваются:
После первого отбора избавились от автоматов, которые не развиваются:
Если нулевой ген равен нулю (если в окружении черной клетки все черные — клетка остается черной) — такие автоматы развиваются с одинаковой скоростью. Автоматы с этим геном (нулевой равен нулю) не соответствуют нашему критерию (наименьшая скорость развития). Количество таких автоматов уменьшается с каждым отбором. Если же нулевой ген равен единице — на первой (нечетной) итерации фон меняется на белый. Далее фон может оставаться белым или мигать (на нечетной итерации — белый, на четной — черный). 30-я итерация, на которой мы производим отбор — четная. Избавившись от автоматов с черным фоном (на 30-й итерации) — избавимся от мигающих (чтобы лишний раз не издеваться над нашими многоуважаемыми эпилептиками).











[1,0,1,1,1,0,0,1,0,0,0,1,0,1,0,1,1,1]

[1,0,0,1,1,0,0,1,1,0,1,0,1,1,0,1,1,1]
Для сравнения случайный автомат:
[1,0,0,1,1,1,0,1,1,1,0,0,1,1,0,0,0,1]

4. Автомат Конвея и ему подобные (2)
В автоматах с правилами Конвеевского типа, мы считаем количество живых (единиц) клеток в окрестности Мура. Эту окрестность можно разбить на 4 пары и считать количество живых клеток в этих парах:
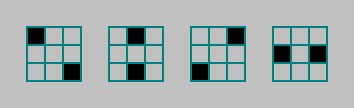
Число:
Вполне астрономическое и сгодится для генетического алгоритма.
Размер генотипа каждой особи — 162 гена:
Заполняем популяцию случайными автоматами
var rulesize=162; for(var n=0;n<PopulationSize;n++){ population[n]=[]; fitness[n]=0; for(var i=0;i<rulesize;i++){ population[n][i]=Math.round(Math.random()); } }Функция fillrule();
function fillrule(){ var r; for(var n=0;n<PopulationSize;n++){ rule[n]=[]; r=population[n]; var q1, q2, q3, q4, q5; var q; for(var i=0;i<512;i++){ var ii=i.toString(2); for(var j=ii.length;j<9;j++) ii='0'+ii; q1=1*ii[4]; q2=1*ii[0]+1*ii[8]; q3=1*ii[1]+1*ii[7]; q4=1*ii[2]+1*ii[6]; q5=1*ii[3]+1*ii[5]; q=parseInt(''+q2+q3+q4+q5,3); if(q1==0) rule[n][i]=r[q]; else rule[n][i]=r[q+81]; } } }















А поиграться?
А поиграться можно здесь:
Двухмерные клеточные автоматы второго порядка. Интерфейс:
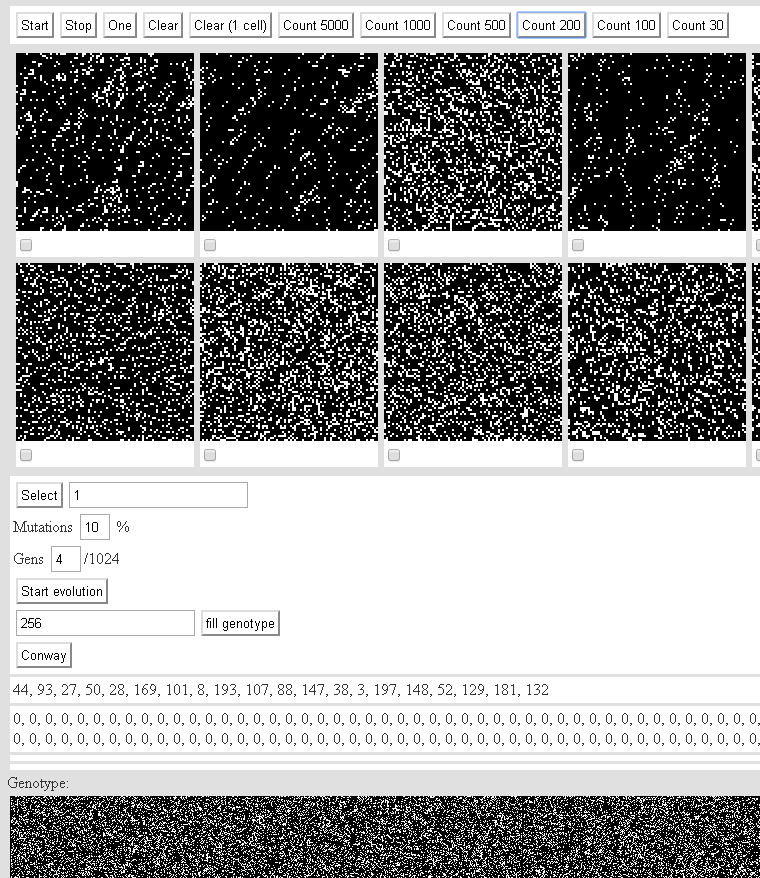
Gens — число мутирующих генов.
Start evolution — запускает механизм скрещиваний и мутаций.
Fill genotype — заполняет указанное число генов в генотипе каждого автомата.
Conway — заполняет популяцию автоматами Конвеевского типа.
Ниже две строки:
Номера показанных автоматов.
Содержимое массива fenotype.
Генофонд популяции еще ниже.
Весь прогресс сохраняется в локальном хранилище (Local Storage).
С автоматами Конвеевского типа (с теми, которые рассмотрены в статье последними) можно поиграться здесь:
4. Автомат Конвея и ему подобные (2).
Источник: habr.com