Нахождение объектов без учителя (Unsupervised Object Detection)

Одна из важнейших задач в машинном обучении — детектирование объектов (Object Detection). Недавно был опубликован ряд алгоритмов машинного обучения основанных на глубоком обучении (Deep Learning) для детектирования объектов. Эти алгоритмы занимают одно из центральных мест в практических приложениях компьютерного зрения, в частности, очень популярные сейчас самоуправляемые автомобили (Self-Driving Cars). Но все эти методы являются методами обучения с учителем, т.е. им необходим размеченный набор данных (Dataset) огромного размера. Естественно возникает желание иметь модель способную обучаться на «сырых» (неразмеченных) данных. Я попытался проанализировать существующие методы и также указать возможные пути их развития. Всех желающих милости прошу под кат, будет интересно.

Текущее состояние вопроса

Естественно, что формулировка этой задачи существует уже достаточно давно (чуть ли не с первых дней существования машинного обучения) и есть достаточное количество работ на эту тему. Вот например одна из моих любимых Spatially Invariant Unsupervised Object Detection with Convolutional Neural Networks. Если коротко, то авторы тренируют вариационный автоэнкодер (VAE), но у меня этот подход вызывает ряд вопросов.

Немного философии

Итак, что такое объект на изображении? Для ответа на этот вопрос мы должны ответить на вопрос — а зачем мы вообще разделяем мир на объекты? Немного поразмыслив над этим вопросом, у меня появился всего один ответ на этот вопрос (я не говорю что других не существует, просто я их не нашел) — мы пытаемся найти такое представление мира, которое нам легко понимать и контролировать объем информации необходимый для описания мира в контексте текущей задачи. Например, для задачи классификации изображений (которая вообще говоря сформулирована некорректно — очень редко бывают изображения с одним объектом. т.е. мы решаем задачу не что изображено на картинке, а какой объект «главный») нам достаточно сказать что на картинке «автомобиль», в свою очередь, для задачи детектирования объектов мы хотим знать какие «интересные» объекты (нам ведь неинтересны все листики с деревьев на картинке) там есть, и где они находятся, для задачи описания сцены — мы хотим получить название «интересного» процесса который там происходит, например «закат» и т.д.

Получается что объекты — удобное представление данных. Какими свойствами это представление должно обладать? Представление должно содержать насколько это возможно полную информацию о изображении. Т.е. имея объектное описание, мы хотим уметь восстанавливать исходное изображение с необходимой степенью точности.

Как же это выразить математически? Представим что изображение это реализация случайной величины X, а представление будет реализация случайной величины Y. В силу сказанного выше мы хотим чтобы Y содержала как можно больше информации о X. Естественным образом, для этого использовать понятие взаимной информации (Mutual Information).

Модели машинного обучения для максимума информации

Детектирование объектов можно рассматривать как генеративную модель, которой на вход подается изображение $$, а на выходе получаем объектное представление изображения $$.

Давайте теперь вспомним формулу для вычисления взаимной информации:

$$

где $$ совместная плотность распределение, а $$ маргинальные.

Здесь я не буду углубляться почему эта формула выглядит именно так, но мы будем верить что внутренне она очень логична. Кстати исходя из описанных соображений не обязательно выбирать именно взаимную информацию, это может быть любая другая «информация», но к этому мы еще вернемся ближе к концу.

Особенно внимательные (или те кто читал книги по теории информации) уже заметили что взаимная информация есть не что иное как дивергенция Кульбака-Леблера между совместным распределением и произведением маргинальных. Здесь возникает небольшое осложнение — любой читавший хотя бы пару книжек по машинному обучению знает, что если у нас есть только сэмплы из двух распределений (т.е. мы не знаем функций распределений), то не то что оптимизировать, а даже оценить дивергенцию Кульбака-Лейблера задача весьма нетривиальная. Более того наши горячо любимые GAN и родились именно по этой причине.

К счастью нам на помощь приходит замечательная идея использовать нижнюю вариационную границу описанная в On Variational Bounds of Mutual Information. Взаимную информацию можно представить в виде:

$$

Или

$$

где $$ — распределение представления при заданном изображении, праметризуемая нашей нейро-сеткой и из этого распределения мы умеем семплировать, но оценивать плотность или вероятность того или иного семпла нам уметь не обязательно (что в общем то типично для многих генеративных моделей). $$ — некоторая функция плотности, параметризуемая второй нейро-сеткой (в самом общем случае нам понадобится 2 нейросетки, хотя в некоторых случаях они могут быть представлены 1-ой), тут уже нам обязательно уметь считать вероятности получающихся семплов.

Величина $$ называется нижней вариацинной границей (Lower Variational Bound).

Теперь мы можем решить приближение к нашей задаче, а именно увеличивать не саму взаимную информацию, а ее нижную вариационную границу. Если распределение $$ выбрано правильно, то в максимальная точка вариационной границы и взаимной информации будут совпадать, но в практическом случае (когда распределение $$ не может в точности представить $$, но состоит из достаточно большого семейства функций) будут очень близко, что нас тоже устраивает.

Если кто-то не знает как это работает советую очень внимательно разобраться с EM-алгоритмом. Здесь абсолютно аналогичный случай.

Что же здесь получается? На самом деле деле мы получили функционал для обучения автоэнкодера. Если Y это результат на выходе нейронной сети при некоторой картинке на входе, то это значит что $$, где $$ функция трансформации нейросети. А обратное распределение аппроксимировать гауссовским, т.е $$, получим:

$$

А это классический функционал для автоэнкодера.

Автоэнкодера недостаточно

Думаю что многие уже хотят натренировать автоэнкодер и надеятся что в его скрытом слое будут нейроны которые реагируют на конкретные объекты. Вообще есть подтверждение что-то похожее и получается Building High-level Features Using Large Scale Unsupervised Learning. Но все же это абсолютно непрактично. И особо внимательные уже заметили что авторы этой статьи использовали регуляризацию — добавили слагаемое которое обеспечивает разреженность в скрытом слое, и черным по белому написали, что ничего подобного не происходит без этого слагаемого. Достаточно ли принципа максимизации взаимной информации чтобы выучить «удобное» представление? Очевидно что нет, потому что мы можем Y выбрать равным X (т.е использовать само изображение как его представление) или любое биективное преобразование, взаимная информация обращается в бесконечность в этом случае. Больше этого значения быть не может, а как мы знаем это очень плохое представление.
Нам необходим дополнительный критерий «удобства» представления. Авторы выше описанной статьи взяли разреженность как «удобство». Это своего рода реализации гипотезы что на картинке должно быть немного «важных объектов». Но мы пойдем дальше — нам ведь хочеться не только узнать факт что такой то объект есть на картинке, а еще хочется узнать где он, как сильно перекрыт и т.д. Возникает вопрос, как заставить нейронную сеть интерпретировать выход какого-то из нейронов как, например, координату объекта? Ответ очевиден — выход с этого нейрона должен использоваться именно для этого. Т.е зная представление мы должны уметь генерировать «похожие» картинки на исходную.

Общая идея позаимствована у парней из Фейсбука.
Энкодер будет выглядеть так:

где $$ — некоторый вектор описывающий объект, $$ — координаты объекта, $$ — масштаб объекта, $$ — положение объекта в глубину, $$ — вероятность того что объект присутствует.

Т.е нейросеть на вход получает картинку заранее определенного размера на которой мы хотим найти объекты и выдает массив описаний. Если мы хотим однопроходную сеть, то к сожалению этот массив придется сделать фиксированного размера. Если же хотим находить все объекты, то придется использовать реккуретные сети.

Декодер будет таким:

Где Object Generator — неросеть которая на вход получает вектор описания объекта и выдает $$ — изображение (некоего стандартного размера) объекта и маску непрозрачных пикселей (opacity mask).
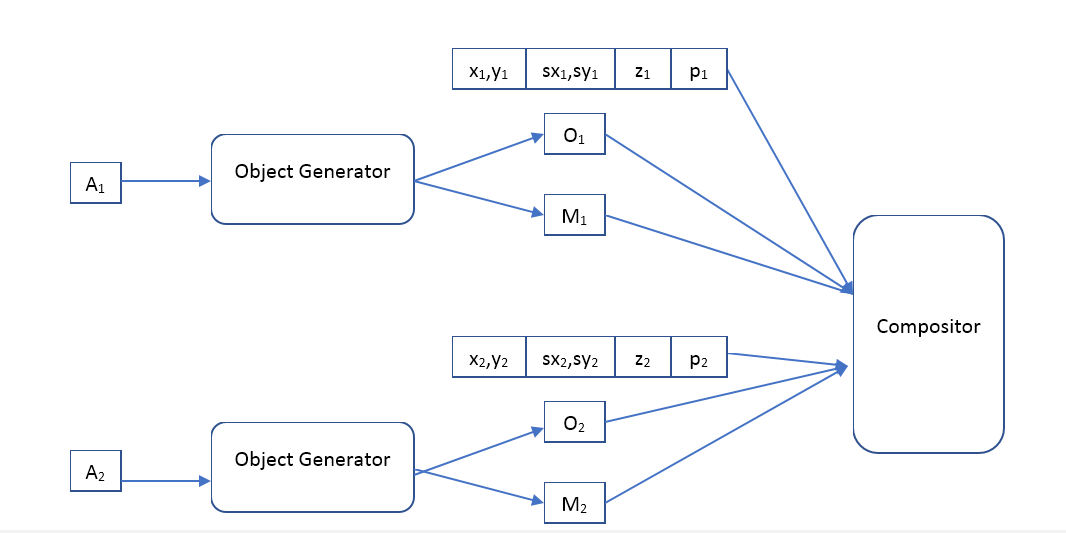
Compositor — получает на вход изображение всех объектов, маску, положение, масштаб, глубину и формирует выходное изображение, которое должно быть похоже на изначальное.

В чем отличие «нашего» подхода от VAE?

Кажется что мы хотим использовать автоэнкодер с той же архитектурой, что и авторы статьи Spatially Invariant Unsupervised Object Detection with Convolutional Neural Networks, так возникает вопрос в чем же разница. И там и там автоэнкодер, только во втором варианте он вариационный. С теоретической точки зрения разница очень большая. VAE — генеративная модель и ее задача сделать 2 распределения (исходных картинок и генерируемых) максимально похожим. Вообще говоря, VAE не дает никаких гарантий что изображение сгенерированное из «описание» объекта сгенерированного из оригинального изображения хоть немного будет похоже на оригинал. Кстати об этом говорят и авторы самого VAE Auto-Encoding Variational Bayes. Так почему же это все таки работает? Я думаю что выбранная архитектура нейросетей и «описания» способствует увеличению взаимной информации изображения и «описания», но никаких математических подтверждений этой гипотезы у меня не получилось найти. Вопрос к читателям, может кто-то сможет объяснить результаты авторов — их восстановленное изображение очень похоже на оригинал, почему? К тому же использование VAE заставляет авторов задавать распределение «описаний», а метод максимизации взаимной информации не делает никаких предположений на этот счет. Что дает нам дополнительную свободу, например, мы можем на уже обученной модели попытаться кластеризовать вектора $$ описаний, и посмотреть — может быть такая система выучит классы объектов? Необходимо заметить, что подобная кластеризация при использовании VAE не имеет никакого смысла, например, авторы статьи используют гауссовское распределение для этих векторов.

Эксперименты

К сожалению, сейчас работа занимает огромное кол-во времени и довести до конца в приемлемое кол-во времени не получается. Если кто-то хочет написать несколько тысяч строк кода, обучить сотни моделей машинного обучения и провести много интерсных экспериментов, просто потому что ему (или ей) это приносит удовольствие — буду рад объединить усилия. Пишите в личку.

Поле для экспериментов здесь очень широкое. У меня в планах начать с обучения классического автоэнкодера (детерминированного отображения изображений на описания и гауссовского обратного распределения) и посмотреть что он выучивает. В первых экспериментах будет достаточным использовать композитор описанный парнями из Фейсбука, но в дальнейшем думаю будет очень интересно поиграться с различными композиторами, и возможно сделать их тоже обучаемыми. Сравнить различные регуляризаторы: без него, Sparse и т.д. Сравнить использование однопроходных (feedforward) и рекурентных моделей. Потом использовать более продвинутые модели распределений для обратного распределения, например, такую Density estimation using Real NVP. Посмотреть насколько лучше или хуже становится с более гибкими моделями. Посмотреть, что будет происходить если отображение изображений на описания сделать не детерминированным (генерировать из некоторого условного распределения). Ну и наконец, попытаться применить различные методы кластеризации к векторам описаний $$ и понять, может ли такая система выучить классы объектов.

Ну а самое главное, очень хочется сравнить качество модели основанной на максимизации взаимной информации и модели с VAE.