Геометрия машинного обучения. Разделяющие гиперплоскости или в чём геометрический смысл линейной комбинации?

МЕНЮ

Искусственный интеллект
Поиск
Регистрация на сайте
Помощь проекту

ТЕМЫ

Новости ИИРазработка ИИВнедрение ИИРабота разума и сознаниеМодель мозгаРобототехника, БПЛАТрансгуманизмОбработка текстаТеория эволюцииДополненная реальностьЖелезоКиберугрозыНаучный мирИТ индустрияРазработка ПОТеория информацииМатематикаЦифровая экономика

Авторизация

RSS

RSS новости
Во многих алгоритмах машинного обучения, в том числе в нейронных сетях, нам постоянно приходится иметь дело со взвешенной суммой или, иначе, линейной комбинацией компонент входного вектора. А в чём смысл получаемого скалярного значения?

В статье попробуем ответить на этот вопрос с примерами, формулами, а также множеством иллюстраций и кода на Python, чтобы вы могли легко всё воспроизвести и поставить свои собственные эксперименты.

Модельный пример

Чтобы теория не отрывалась от реальных кейсов, возьмём в качестве примера задачу бинарной классификации. Есть датасет: m образцов, каждый образец — n-мерная точка. Для каждого образца мы знаем к какому классу он относится (зелёный или красный). Также известно, что датасет является линейно разделимым, т.е. существует n-мерная гиперплоскость такая, что зелёные точки лежат по одну сторону от неё, а красные — по другую.

image
К решению задачи поиска такой гиперплоскости можно подходить разными способами, например с помощью логистической регрессии (logistic regression), метода опорных векторов с линейным ядром (linear SVM) или взять простейшую нейросеть:
image
В конце статьи мы с нуля напишем механизм обучения персептрона и решим задачу бинарной классификации своими руками, используя полученные знания.

От прямой линии до гиперплоскости

Рассмотрим подробную математику для прямой. Для общего случая гиперплоскости в n-мерном пространстве будет всё ровно тоже самое, с поправкой на количество компонент в векторах.

image
Прямая линия на плоскости задаётся тремя числами — $(w_1, w_2, b)$:

$w_1 x_1 + w_2 x_2 + b = 0 $ или:

$sum_{i = 1}^{2}{w_ix_i}+b=0 $ или:

$w^Tx+b=0 $ Первые два коэффициента $w_1, w_2$ задают всё семейство прямых линий, проходящих через точку (0, 0). Соотношение между $w_1$ и $w_2$ определяет угол наклона прямой к осям.

Если $w_1 = w_2$, получаем линию, идущую под углом 45 градусов ($frac{pi}{4}$) к осям $x_1$ и $x_2$ и делящую первый/третий квадранты пополам.

Ненулевой коэффициент $b$ позволяет линии не проходить через ноль. При этом наклон к осям $x_1$ и $x_2$ не меняется. Т.е. $b$ задаёт семейство параллельных линий:

image
Геометрический смысл вектора $(w1, w2)$ — это нормаль к прямой $w_1 x_1 + w_2 x_2 + b = 0$:

(Если не учитывать смещение $b$, то $w^Tx$ — это не более чем скалярное произведение двух векторов. Равенство нулю равносильно их ортогональности. Следовательно, $x$ — семейство векторов, ортогональных $(w_1, w_2)$.)

image
P.S. Понятно, что таких нормалей бесконечно много, как и троек (w1, w2, b) задающих прямую. Если все три числа умножить на ненулевой коэффициент $k$ — прямая останется той же.

В общем случае n-мерного пространства, $(w_1, ..., w_n, b)$ задаёт n-мерную гиперплоскость.

$w_1 x_1 + w_2 x_2 + ... + w_n x_n + b = 0 $ или:

$sum_{i = 1}^{n}{w_ix_i}+b=0 $ или:

$w^Tx+b=0 $

Геометрический смысл линейной комбинации

Если точка $x (x_0,...,x_n)$ лежит на гиперплоскости, то

$w^Tx+b=0 $ А что происходит с этой суммой, если точка не лежит на плоскости?

Гиперплоскость делит гиперпространство на два гиперподпространства. Так вот точки, находящиеся в одном из этих подпространств (условно говоря «выше» гиперплоскости), и точки, находящиеся в другом из этих подпространств (условно говоря «ниже» гиперплоскости), будут в этой сумме давать разный знак:

$w^T x + b > 0$ — точка лежит «выше» гиперплоскости

$w^T x + b < 0$ — точка лежит «ниже» гиперплоскости

Это очень важное наблюдение, поэтому предлагаю его перепроверить простым кодом на Python:

Код примера на Python 
# для красоты # можете закомментировать, если у вас не установлен этот пакет import seaborn  import matplotlib.pyplot as plt import numpy as np  # наша линия: w1 * x1 + w2 * x2 + b = 0 def line(x1, x2):     return -3 * x1 - 5 * x2 - 2  # служебная функция в форме x2 = f(x1) (для наглядности) def line_x1(x1):     return (-3 * x1 - 2) / 5  # генерируем диапазон точек np.random.seed(0) x1x2 = np.random.randn(200, 2) * 2  # рисуем точки for x1, x2 in x1x2:     value = line(x1, x2)      if (value == 0): # синие — на линии         plt.plot(x1, x2, 'ro', color='blue')     elif (value > 0): # зелёные — выше линии         plt.plot(x1, x2, 'ro', color='green')     elif (value < 0): # красные — ниже линии         plt.plot(x1, x2, 'ro', color='red')  # выставляем равное пиксельное  разрешение по осям plt.gca().set_aspect('equal', adjustable='box')              # рисуем саму линию x1_range = np.arange(-5.0, 5.0, 0.5) plt.plot(x1_range, line_x1(x1_range), color='blue')  # проставляем названия осей plt.xlabel('x1') plt.ylabel('x2')  # на экран! plt.show()
image
Нужно понимать, что «выше» и «ниже» здесь — понятия условные. Это специально отражено в примере — зелёные точки оказываются визуально ниже. С геометрической точки зрения направление «выше» для данной конкретной линии определяется вектором нормали. Куда смотрит нормаль, там и верх:
image
Т.о. знак линейной комбинации позволяет отнести точку к верхнему или нижнему подпространству.
А значение? Значение (по модулю) определяет удалённость точки от плоскости:

$dist(x) = frac{|w^Tx+b|}{||w||}$

Т.е. чем дальше от плоскости находится точка, тем больше будет значение линейной комбинации для неё. Если зафиксировать значение линейной комбинации, получим точки, лежащие на прямой, параллельной исходной.

Опять же, наблюдение важное, поэтому перепроверяем:

Код примера на Python 
# для красоты # для красоты # можете закомментировать, если у вас не установлен этот пакет import seaborn  import matplotlib.pyplot as plt import numpy as np  # наша линия: w1 * x1 + w2 * x2 + b = 0 def line(x1, x2):     return -3 * x1 - 5 * x2 - 2  # служебная функция в форме x2 = f(x1) (для наглядности) def line_x1(x1):     return (-3 * x1 - 2) / 5  # генерируем диапазон точек np.random.seed(0) x1x2 = np.random.randn(200, 2) * 2  # рисуем точки for x1, x2 in x1x2:         value = line(x1, x2)      # цвет тем тенее, чем меньше значение — поэтому минус     # коэффициенты — чтобы попасть в диапазон [0, 0.75]     # чёрный (0) — самые удалённые точки, светло-серый (0.75) — самые близкие     color = str(max(0, 0.75 - np.abs(value) / 30))      plt.plot(x1, x2, 'ro', color=color)          # выставляем равное пиксельное  разрешение по осям plt.gca().set_aspect('equal', adjustable='box')          # рисуем саму линию x1_range = np.arange(-5.0, 5.0, 0.5) plt.plot(x1_range, line_x1(x1_range), color='blue')  # проставляем названия осей plt.xlabel('x1') plt.ylabel('x2')  # на экран! plt.show()
image
Всё сходится.

Выводы

  • Линейная комбинация позволяет разделить n-мерное пространство гиперплоскостью.
  • Точки по разные стороны гиперплоскости будут иметь разный знак линейной комбинации $w^Tx+b$.
  • Чем точка удалённее от гиперплоскости, тем абсолютное значение линейной комбинации будет больше.

С точки зрения бинарной классификации последнее утверждение можно переформулировать следующим образом. Чем удалённее точка от гиперплоскости, являющейся границей решений (decision boundary), тем увереннее мы в том, что наш образец (sample) определяемый этой точкой попадает в тот или иной класс.

Близко и далеко: это как?

Близко и далеко — понятия сугубо субъективные. А при классификации отвечать нам нужно чётко — либо деталь годится для строительства ракеты для полёта на Марс, либо это брак. Либо человек кликнет по рекламе, либо нет. Возможно ответить с долей уверенности — дать вероятность позитивного (true) исхода.

Для этого к линейной комбинации можно применить функцию активации (в терминологии нейросетей).

Если применить логистическую функцию (график смотри ниже):

$logistic(x) = frac{1}{1 + e^{-x}}$

получаем на выходе вероятности и такую картинку:

Код примера на Python 
# для красоты # можете закомментировать, если у вас не установлен этот пакет import seaborn  import matplotlib.pyplot as plt import numpy as np  # логистическая функция def logit(x):     return 1 / (1 + np.exp(-x))  # наша линия: w1 * x1 + w2 * x2 + b = 0 def line(x1, x2):     return 3 * x1 + 5 * x2 + 2  # служебная функция в форме x2 = f(x1) (для наглядности) def line_x1(x1):     return (-3 * x1 - 2) / 5  # генерируем диапазон точек np.random.seed(0) xy = np.random.randn(200, 2) * 2  # рисуем точки for x1, x2 in x1x2:         # деление добавляется для наглядности — эдакая ручная нормализация     value = logit(line(x1, x2) / 2)      if (value < 0.001):         color = 'red'     elif (value > 0.999):         color = 'green'     else:         color = str(0.75 - value * 0.5)      plt.plot(x1, x2, 'ro', color=color)          # выставляем равное пиксельное  разрешение по осям plt.gca().set_aspect('equal', adjustable='box')          # рисуем саму линию x1_range = np.arange(-5.0, 5.0, 0.5) plt.plot(x1_range, line_x1(x1_range), color='blue')  # проставляем названия осей plt.xlabel('x1') plt.ylabel('x2')  # на экран! plt.show()
image
Красные — точно нет (false, точно брак, точно не кликнет). Зелёные — точно да (true, точно годится, точно кликнет). Всё, что в определённом диапазоне близости от гиперплоскости (граница решений) получает некоторую вероятность. На самой прямой вероятность ровно 0.5.
P.S. «Точно» здесь определяется как меньше 0.001 или больше 0.999. Сама логистическая функция стремится к нулю на минус бесконечности и к единице на плюс бесконечности, но никогда этих значений не принимает.

N.B. Обратите внимание, что данный пример лишь демонстрирует каким образом можно ужать (squashing) расстояние со знаком в интервал вероятностей $(0, 1)$. В практических задачах для поиска оптимального отображения используется калибровка вероятностей. Например, в алгоритме шкалирования по Платту (Platt scaling) логистическая функция параметризуется:

$f(x) = frac{1}{1 + e^{Ax + B}}$

и затем коэффициенты $A$ и $B$ подбираются машинным обучением. Подробнее смотрите: binary classifier calibration, probability calibration.

image

В каком мы пространстве? (полезное умозрительное упражнение)

Казалось бы понятно — мы в пространстве данных $X$ (data space), в котором лежат образцы $x$. И ищем оптимальное разделение плоскостью, определяемой вектором $w$.

$w^T x + b > 0$ для зелёных точек
$w^T x + b < 0$ для красных точек

Но в нашей задаче бинарной классификации образцы зафиксированы, а веса меняются. Соответственно мы можем всё переиграть, перейдя в пространство весов $W$ (weight space):

$x^T w + b$ Образцы из тренировочного набора $x_1 ... x_m$ в этом случае задают $m$ гиперплоскостей и наша задача в том, чтобы найти такую точку $w$, которая бы лежала с нужной стороны от каждой плоскости. Если исходный датасет является линейно-разделимым, то такая точка найдётся.

image
Код примера на Python 
# для красоты # можете закомментировать, если у вас не установлен этот пакет import seaborn  import matplotlib.pyplot as plt import numpy as np  # образец 1 def line1(w1, w2):     return -3 * w1 - 5 * w2 - 8  # служебная функция в форме w2 = f1(w1) (для наглядности) def line1_w1(w1):     return (-3 * w1 - 8) / 5  # образец 2 def line2(w1, w2):     return 2 * w1 - 3 * w2 + 4  # служебная функция в форме w2 = f2(w1) (для наглядности) def line2_w1(w1):     return (2 * w1 + 4) / 3  # образец 3 def line3(w1, w2):     return 1.2 * w1 - 3 * w2 + 4  # служебная функция в форме w2 = f2(w1) (для наглядности) def line3_w1(w1):     return (1.2 * w1 + 4) / 3  # образец 4 def line4(w1, w2):     return -5 * w1 - 5 * w2 - 8  # служебная функция в форме w2 = f2(w1) (для наглядности) def line4_w1(w1):     return (-5 * w1 - 8) / 5  # генерируем диапазон точек w1_range = np.arange(-5.0, 5.0, 0.5) w2_range = np.arange(-5.0, 5.0, 0.5)  # рисуем веса (w1, w2), лежащие по нужные стороны от образцов for w1 in w1_range:     for w2 in w2_range:         value1 = line1(w1, w2)         value2 = line2(w1, w2)         value3 = line3(w1, w2)         value4 = line4(w1, w2)                  if (value1 < 0 and value2 > 0 and value3 > 0 and value4 < 0):             color = 'green'         else:             color = 'pink'                  plt.plot(w1, w2, 'ro', color=color)  # выставляем равное пиксельное  разрешение по осям plt.gca().set_aspect('equal', adjustable='box')              # рисуем саму линию (гиперплоскость) для образца 1 plt.plot(w1_range, line1_w1(w1_range), color='blue') # для образца 2 plt.plot(w1_range, line2_w1(w1_range), color='blue') # для образца 3 plt.plot(w1_range, line3_w1(w1_range), color='blue') # для образца 4 plt.plot(w1_range, line4_w1(w1_range), color='blue')  # рисуем только эту область — остальное не интересно plt.axis([-7, 7, -7, 7])  # проставляем названия осей plt.xlabel('w1') plt.ylabel('w2')  # на экран! plt.show()
При обучении модели удобнее рассуждать в пространстве весов, т.к. обновляются веса, а вектора-образцы из тренировочного набора задают нормали к гиперплоскостям. Например:

image
Предположим, что образцу $x$ соответствует зелёный класс, соответствующий неравенству:

$x^T w + b > 0$ Т.к. на иллюстрации вектор $w$ смотрит против нормали $x$, то значение линейной комбинации будет отрицательным — следовательно мы имеем ошибку классификации.

Соответственно необходимо обновить вектор $w$ в сторону, указываемую нормалью:

$w_{new} = w_{old} + lambda x$, где $lambda > 0$

с некоторой «скоростью» $lambda$. Тем самым на следующем шаге предсказание будет либо верным, либо менее неверным, т.к. слагаемое $lambda x$, сонаправленное с нормалью, «довернёт» вектор весов в зелёную область.

Практика. Обучаем персептрон

Для решения задачи бинарной классификации в случае линейной разделимости образцов можно обучить простейший персептрон, устроенный по такой схеме:

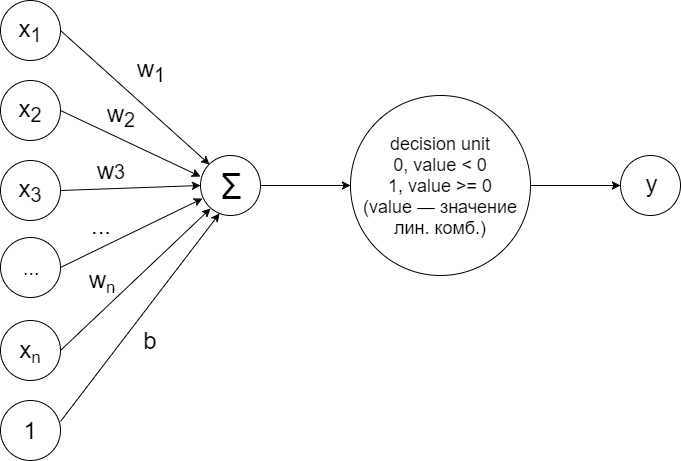
image
Эта конструкция реализует ровно тот принцип, который был описан выше. Вычисляется линейная комбинация:
$sum_{i = 1}^{n}{w_ix_i}+b$ По значению которой решатель (decision unit) принимает решение отнести образец к одному из двух классов по следующему принципу:

$w^T x + b ge 0$ класс +1 (зелёные точки)
$w^T x + b < 0$ класс -1 (красные точки)

Изначально веса инициализируются случайным образом, а на каждом шаге обучения для каждого образца проделывается следующий алгоритм:

Вычисляется предсказание (predicted label). Если оно не совпадает с реальным классом, то веса обновляются по следующему принципу:

$w_{new} = w_{old} + y_nx_n b_{new} = b_{old} + y_n$

где $y_n$ — реальный класс образца $x_n$. Почему это работает описано выше в умозрительном упражнении с переходом в пространство весов. Кратко:

  • Доворачиваем вектор-вес в сторону верного класса: по нормали $x_n$ в случае класса +1; против нормали $x_n$ в случае класса -1. (Сама нормаль всегда смотрит в сторону класса +1.)
  • Обновляем смещение по аналогичному принципу.

Вот что получается:

image
Код на Python 
# для красоты # можете закомментировать, если у вас не установлен этот пакет import seaborn  # необходимые пакеты import matplotlib.pyplot as plt import numpy as np  # воспроизводимость — наше всё np.random.seed(17)  # генерируем диапазон зелёных точек x1x2_green = np.random.randn(200, 2) * 2 + 21  # генерируем диапазон красных точек x1x2_red = np.random.randn(200, 2) * 4 + 5  # все яйца в одну корзину x1x2 = np.concatenate((x1x2_green, x1x2_red))  # проставляем классы: зелёные +1, красные -1 labels = np.concatenate((np.ones(x1x2_green.shape[0]), -np.ones(x1x2_red.shape[0])))  # хорошенько перемешиваем indices = np.array(range(x1x2.shape[0])) np.random.shuffle(indices) x1x2 = x1x2[indices] labels = labels[indices]  # случайные начальные веса w1_ = -1.1 w2_ = 0.5 b_ = -20  # разделяющая гиперплоскость (граница решений) def lr_line(x1, x2):     return w1_ * x1 + w2_ * x2 + b_  # ниже границы -1 # выше +1 def decision_unit(value):     return -1 if value < 0 else 1  # добавляем начальное разбиение в список lines = [[w1_, w2_, b_]]  for max_iter in range(100):     # счётчик неверно классифицированных примеров     # для ранней остановки     mismatch_count = 0          # по всем образцам     for i, (x1, x2) in enumerate(x1x2):         # считаем значение линейной комбинации на гиперплоскости         value = lr_line(x1, x2)                  # класс из тренировочного набора (-1, +1)         true_label = int(labels[i])                  # предсказанный класс (-1, +1)         pred_label = decision_unit(value)                  # если имеет место ошибка классификации         if (true_label != pred_label):             # корректируем веса в сторону верного класса, т.е.             # идём по нормали — (x1, x2) — в случае класса +1             # или против нормали — (-x1, -x2) — в случае класса -1             # т.к. нормаль всегда указывает в сторону +1             w1_ = w1_ + x1 * true_label             w2_ = w2_ + x2 * true_label                          # смещение корректируется по схожему принципу             b_ = b_ + true_label                          # считаем количество неверно классифицированных примеров             mismatch_count = mismatch_count + 1          # если была хотя бы одна коррекция     if (mismatch_count > 0):         # запоминаем границу решений         lines.append([w1_, w2_, b_])     else:         # иначе — ранняя остановка         break  # рисуем точки (по последней границе решений) for i, (x1, x2) in enumerate(x1x2):     pred_label = decision_unit(lr_line(x1, x2))      if (pred_label < 0):         plt.plot(x1, x2, 'ro', color='red')     else:         plt.plot(x1, x2, 'ro', color='green')  # выставляем равное пиксельное разрешение по осям plt.gca().set_aspect('equal', adjustable='box')      # проставляем названия осей plt.xlabel('x1') plt.ylabel('x2')  # служебный диапазон для визуализации границы решений x1_range = np.arange(-30, 50, 0.1)  # функционал, возвращающий границу решений в пригодном для отрисовки виде # x2 = f(x1) = -(w1 * x1 + b) / w2 def f_lr_line(w1, w2, b):     def lr_line(x1):         return -(w1 * x1 + b) / w2          return lr_line  # отрисовываем историю изменения границы решений it = 0 for coeff in lines:     lr_line = f_lr_line(coeff[0], coeff[1], coeff[2])          plt.plot(x1_range, lr_line(x1_range), label = 'it: ' + str(it))          it = it + 1      # зум plt.axis([-15, 30, -15, 30])      # легенда plt.legend(loc = 'lower left')    # на экран! plt.show()
Заглянем теперь в пространство весов $W$ (weight space):
image
Код на Python 
# N.B. Этот код не является самостоятельным. Сперва запустите основной код обучения персептрона.          # диапазон весов по оси w1_range = np.arange(0, 10, 0.1)  for i, (x1, x2) in enumerate(x1x2):     if (labels[i] == 1):         color = 'green'     else:         color = 'red'      # линия x1 * w1 + x2 * w2 + b = 0     # в форме w2 = f(w1)     # (для визуализации)     def line(w1):         return -(x1 * w1 + b_) / x2          # русуем образцы; в пространстве весов — это линии     plt.plot(w1_range, line(w1_range), color = color)      # рисуем финальный вес, полученный после обучения персептрона plt.plot(w1_, w2_, 'ro', color='blue')  # зум plt.axis([0, 10, 0, 10])      # выставляем равное пикслельное разрешение по осям plt.gca().set_aspect('equal', adjustable='box')  # проставляем названия осей plt.xlabel('w1') plt.ylabel('w2')          # на экран! plt.show()
Красные и зелёные линии — это исходные образцы, синяя точка — итоговый вес.
А какие ещё веса дают верную классификацию? Смотрим:
image
Код на Python 
# N.B. Этот код не является самостоятельным. Сперва запустите основной код обучения персептрона.          # диапазон в пространстве весов w1_range = np.arange(0, 10, 0.5) w2_range = np.arange(0, 10, 0.5)  # рисуем образцы, терерь уже линиями for i, (x1, x2) in enumerate(x1x2):     def line(w1):         return -(x1 * w1 + b_) / x2              if (labels[i] == 1):         color = 'green'     else:         color = 'red'                 plt.plot(x1_range, line(x1_range), color = color)          # рисуем финальный вес (точка), полученный в ходе обучения персептрона plt.plot(w1_, w2_, 'ro', color='blue')  # линейная комбинация def f(w1, w2, x1, x2):         value = x1 * w1 + x2 * w2 + b_                  return -1 if value < 0 else 1  # будем запоминать хорошие веса (дающие правильную классификацию) # чтобы потом отсмотреть их в простанстве данных (data space) good_weights = []  # перебором ищем все веса, которые лежат с нужной стороны от всех образцов # нужная сторона определяется классом образца for w1 in w1_range:     for w2 in w2_range:         in_range = True                  for i, (x1, x2) in enumerate(x1x2):             if (labels[i] != f(w1, w2, x1, x2)):                 in_range = False                 break                          if (in_range):             good_weights.append([w1, w2, b_])                          # хорошие веса рисуем фиолетовым (точки)             plt.plot(w1, w2, 'ro', color = 'magenta')      # зум plt.axis([0, 10, 0, 10])      # выставляем равное пикслельное разрешение по осям plt.gca().set_aspect('equal', adjustable='box')  # проставляем названия осей plt.xlabel('w1') plt.ylabel('w2')     # на экран! plt.show()  # разделяющая гиперплоскость (граница решений) def lr_line(x1, x2):     return w1_ * x1 + w2_ * x2 + b_  # ниже границы -1 # выше +1 def decision_unit(value):     return -1 if value < 0 else 1  # рисуем точки (по последней границе решений) for i, (x1, x2) in enumerate(x1x2):     pred_label = decision_unit(lr_line(x1, x2))      if (pred_label < 0):         plt.plot(x1, x2, 'ro', color='red')     else:         plt.plot(x1, x2, 'ro', color='green')  # служебный диапазон для визуализации хороших весов x1_range = np.arange(-30, 50, 0.1)                          for (w1, w2, _b) in good_weights:     # веса опять стали коэффициентами, а x1, x2 — переменными     def w_line(x1):         return -(w1 * x1 + b_) / w2          # граница решений в пространстве данных     plt.plot(x1_range, w_line(x1_range))  # зум plt.axis([0, 25, 0, 25])             # выставляем равное пикслельное разрешение по осям plt.gca().set_aspect('equal', adjustable='box')          # проставляем названия осей plt.xlabel('x1') plt.ylabel('x2')          # на экран! plt.show()
Красные и зелёные линии — это исходные образцы, синяя точка — итоговый вес, фиолетовые точки — другие возможные веса.
И выворачиваем всё наизнанку ещё раз, переходя опять в пространство данных $X$ (data space):

image
Те веса, которые в пространстве весов на иллюстрации выше были отмечены фиолетовыми точками, здесь, в пространстве данных, стали линиями других возможных границ решения.
Упражнение (простое): На последней иллюстрации четыре характерных пучка линий. Найдите их среди фиолетовых точек в пространстве весов.

От автора

Спасибо всем хабровчанам за критические отзывы касательно первой версии статьи, в том числе yorko, который вместе с сообществом Open Data Science делает суперский открытый курс по машинному обучению — всем рекомендую. Стало понятно, что материалу не хватает финального штриха и статья была отправлена на доработку. Вторая (она же текущая) версия дополнена примером обучения персептрона.

Итоги

Надеюсь эта статья позволит вам лучше понять и прочувствовать геометрический смысл линейных комбинаций. Ниже приведены ссылки на материалы, использованные при подготовке статьи и интересные с точки зрения углубления в тему. (Все материалы на английском языке.)


Источник: habr.com

Комментарии: