Дискретная математика при внедрении WMS-системы: кластеризация партий товаров на складе

В статье рассказывается как при внедрении WMS-системы мы столкнулись с необходимостью решения нестандартной задачи кластеризации и какими алгоритмами мы ее решали. Расскажем, как мы применяли системный, научный подход к решению проблемы, с какими сложностями столкнулись и какие уроки вынесли.

Эта публикация начинает цикл статей, в которых мы делимся своим успешным опытом внедрения алгоритмов оптимизации в складские процессы. Целью цикла статей ставится познакомить аудиторию с видами задач оптимизации складских операций, которые возникают практически на любом среднем и крупном складе, а также рассказать про наш опыт решения таких задач и встречающиеся на этом пути подводные камни. Статьи будут полезны тем, кто работает в отрасли складской логистики, внедряет WMS-системы, а также программистам, которые интересуются приложениями математики в бизнесе и оптимизацией процессов на предприятии.

Узкое место в процессах

В 2018 году мы сделали проект по внедрению WMS-системы на складе компании «Торговый дом «ЛД» в г. Челябинске. Внедрили продукт «1С-Логистика: Управление складом 3» на 20 рабочих мест: операторы WMS, кладовщики, водители погрузчиков. Склад средний около 4 тыс. м2, количество ячеек 5000 и количество SKU 4500. На складе хранятся шаровые краны собственного производства разных размеров от 1 кг до 400 кг. Запасы на складе хранятся в разрезе партий, так как есть необходимость отбора товара по FIFO.

При проектировании схем автоматизации складских процессов мы столкнулись с существующей проблемой неоптимального хранения запасов. Специфика хранения и укладки кранов такая, что в одной ячейке штучного хранения может находиться только номенклатура одной партии. Продукция приходит на склад ежедневно и каждый приход – это отдельная партия. Итого, в результате 1 месяца работы склада создаются 30 отдельных партий, притом, что каждая должна хранится в отдельной ячейке. Товар зачастую отбирается не целыми палетами, а штуками, и в результате в зоне штучного отбора во многих ячейках наблюдается такая картина: в ячейке объемом более 1м3 лежит несколько штук кранов, которые занимают менее 5-10% от объема ячейки.

Рис 1. Фото нескольких штук товара в ячейке

На лицо неоптимальное использование складских мощностей. Чтобы представить масштаб бедствия могу привести цифры: в среднем таких ячеек объемом более 1м3 с «мизерными» остатками в разные периоды работы склада насчитывается от 100 до 300 ячеек. Так как склад относительно небольшой, то в сезоны загрузки склада этот фактор становится «узким горлышком» с сильно тормозит складские процессы.

Идея решения проблемы

Возникла идея: партии остатков с наиболее близкими датами приводить к одной единой партии и такие остатки с унифицированной партией размещать компактно вместе в одной ячейке, или в нескольких, если места в одной не будет хватать на размещение всего количества остатков.

Рис.2. Схема сжатия остатков в ячейках

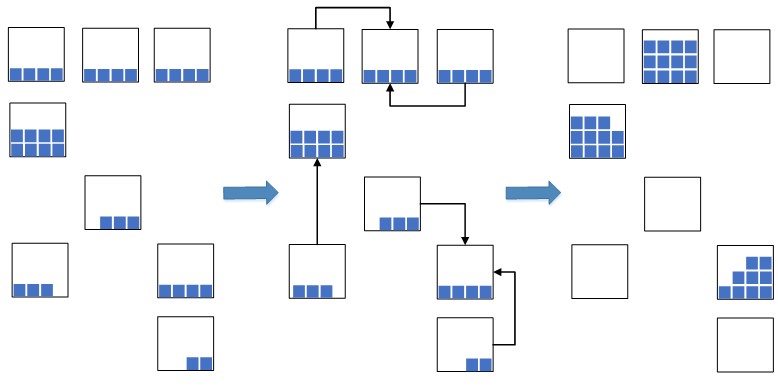
Это позволяет значительно сократить занимаемые складские площади, которые будут использоваться под новый размещаемый товар. В ситуации с перегрузкой складских мощностей такая мера является крайне необходимой, в противном случае свободного места под размещение нового товара может попросту не хватить, что приведет к стопору складских процессов размещения и подпитки. Раньше до внедрения WMS-системы такую операцию выполняли вручную, что было не эффективно, так как процесс поиска подходящих остатков в ячейках был достаточно долгим. Сейчас с внедрением WMS-системы решили процесс автоматизировать, ускорить и сделать его интеллектуальным.

Процесс решения такой задачи разбивается на 2 этапа:

• на первом этапе мы находим близкие по дате группы партий для сжатия;
• на втором этапе мы для каждой группы партий вычисляем максимально компактное размещение остатков товара в ячейках.

В текущей статье мы остановимся на первом этапе алгоритма, а освещение второго этапа оставим для следующей статьи.

Поиск математической модели задачи

Перед тем как садиться писать код и изобретать свой велосипед, мы решили подойти к такой задаче научно, а именно: сформулировать ее математически, свести к известной задаче дискретной оптимизации и использовать эффективные существующие алгоритмы для ее решения или взять эти существующие алгоритмы за основу и модифицировать их под специфику решаемой практической задачи.

Так как из бизнес-постановки задачи явно следует, что мы имеем дело с множествами, то сформулируем такую задачу в терминах теории множеств.

Пусть $$ – множество всех партий остатков некоторого товара на складе. Пусть $$ – заданная константа дней. Пусть $$ – подмножество партий, где разница дат для всех пар партий подмножества не превосходит константы $$. Требуется найти минимальное количество непересекающихся подмножеств $$, такое что все подмножества $$ в совокупности давали бы множество $$.

Иными словами, нам нужно найти группы или кластеры схожих партий, где критерий схожести определяется константой $$. Такая задача напоминает нам хорошо известную всем задачу кластеризации. Важно сказать, что рассматриваемая задача отличается от задачи кластеризации, тем что в нашей задаче есть жестко заданное условие по критерию схожести элементов кластера, определяемое константой $$, а в задаче кластеризации такое условие отсутствует. Постановку задачи кластеризации и информацию по этой задаче можно найти здесь. Итак, нам удалось сформулировать задачу и найти классическую задачу с похожей постановкой. Теперь необходимо рассмотреть общеизвестные алгоритмы для ее решения, чтобы не изобретать велосипед заново, а взять лучшие практики и применить их. Для решения задачи кластеризации мы рассматривали самые популярные алгоритмы, а именно: $$-means, $$-means, алгоритм выделения связных компонент, алгоритм минимального остовного дерева. Описание и разбор таких алгоритмов можно найти здесь. Для решения нашей задачи алгоритмы кластеризации $$-means и $$-means не применимы вовсе, так как заранее никогда не известно количество кластеров $$ и такие алгоритмы не учитывают ограничение константы дней. Такие алгоритмы были изначально отброшены из рассмотрения.
Для решения нашей задачи алгоритм выделения связных компонент и алгоритм минимального остовного дерева подходят больше, но, как оказалось, их нельзя применить «в лоб» к решаемой задаче и получить хорошее решение. Чтобы пояснить это, рассмотрим логику работы таких алгоритмов применительно к нашей задаче.

Рассмотрим граф $$, в котором вершины – это множество партий $$, а ребро между вершинами $$ и $$ имеет вес равный разнице дней между партиями $$ и $$. В алгоритме выделения связных компонент задается входной параметр $$, где $$, и в графе $$ удаляются все ребра, для которых вес больше $$. Соединенными остаются только наиболее близкие пары объектов. Смысл алгоритма заключается в том, чтобы подобрать такое значение $$, при котором граф «развалится» на несколько связных компонент, где партии, принадлежащие этим компонентам, будут удовлетворять нашему критерию схожести, определяемому константой $$. Полученные компоненты и есть кластеры.

Алгоритм минимального покрывающего дерева сначала строит на графе $$ минимальное покрывающее дерево, а затем последовательно удаляет ребра с наибольшим весом до тех пор, пока граф не «развалится» на несколько связных компонент, где партии, принадлежащие этим компонентам, будут также удовлетворять нашему критерию схожести. Полученные компоненты и будут кластерами.

При использовании таких алгоритмов для решения рассматриваемой задачи может возникнуть ситуация как на рисунке 3.

Рис 3. Применение алгоритмов кластеризации к решаемой задаче

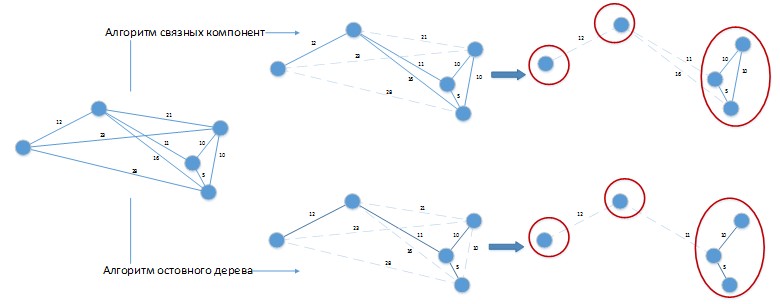
Допустим у нас константа разницы дней партий равна 20 дней. Граф $$ был изображен в пространственном виде для удобства визуального восприятия. Оба алгоритма дали решение с 3-мя кластерами, которое можно легко улучшить, объединив партии, помещенные в отдельные кластеры, между собой! Очевидно, что такие алгоритмы необходимо дорабатывать под специфику решаемой задачи и их применение в чистом виде к решению нашей задачи будет давать плохие результаты.

Итак, прежде чем начинать писать код модифицированных под нашу задачу графовых алгоритмов и изобретать свой велосипед (в силуэтах которого уже угадывались очертания квадратных колес), мы, опять же, решили подойти к такой задаче научно, а именно: попробовать свести ее к другой задаче дискретной оптимизации, в надежде на то, что существующие алгоритмы для ее решения можно будет применить без модификаций. Очередной поиск похожей классической задачи увенчался успехом! Удалось найти задачу дискретной оптимизации, постановка которой 1 в 1 совпадает с постановкой нашей задачи. Этой задачей оказалась задача о покрытии множества. Приведем постановку задачи применительно к нашей специфике.

Имеется конечное множество $$ и семейство $$ всех его непересекающихся подмножеств партий, таких что разница дат для всех пар партий каждого подмножества $$ из семейства $$ не превосходит константы $$. Покрытием называют семейство $$ наименьшей мощности, элементы которого принадлежат $$, такое что объединение множеств $$ из семейства $$ должно давать множество всех партий $$.

Подробный разбор этой задачи можно найти здесь и здесь. Другие варианты практического применения задачи о покрытии и её модификаций можно найти здесь.

Алгоритм решения задачи

С математической моделью решаемой задачи определились. Теперь приступим к рассмотрению алгоритма для ее решения. Подмножества $$ из семейства $$ можно легко найти следующей процедурой.

1. Упорядочить партии из множества $$ в порядке убывания их дат.
2. Найти минимальную и максимальную даты партий.
3. Для каждого дня $$ от минимальной даты до максимальной найти все партии, даты которых отличаются от $$ не более чем на $$ (поэтому значение $$ лучше брать четное).

Логика работы процедуры формирования семейства множеств $$ при $$ дней представлена на рисунке 4.

Рис.4. Формирование подмножеств партий

В такой процедуре необязательно для каждого $$ перебирать все другие партии и проверять разность их дат, а можно от текущего значения $$ двигаться влево или право до тех пор, пока не нашли партию, дата которой отличается от $$ более чем на половинное значение константы. Все последующие элементы при движении как вправо, так и влево будут нам не интересны, так как для них различие в днях будет только увеличиваться, поскольку элементы в массиве были изначально упорядочены. Такой подход будет существенно экономить время, когда число партий и разброс их дат значительно большие.

Задача о покрытии множества является $$-трудной, а значит для её решения не существует быстрого (с временем работы равному полиному от входных данных) и точного алгоритма. Поэтому для решения задачи о покрытии множества был выбран быстрый жадный алгоритм, который конечно не является точным, но обладает следующими достоинствами:

• Для задач небольшой размерности (а это как раз наш случай) вычисляет решения достаточно близкие к оптимуму. С ростом размера задачи качество решения ухудшается, но всё же довольно медленно;
• Очень прост в реализации;
• Быстр, так как оценка его времени работы равна $$.

Жадный алгоритм выбирает множества руководствуясь следующим правилом: на каждом этапе выбирается множество, покрывающее максимальное число ещё не покрытых элементов. Подробное описание алгоритма и его псевдокод можно найти здесь. Сравнение точности такого жадного алгоритма на тестовых данных решаемой задачи с другими известными алгоритмами, такими как вероятностный жадный алгоритм, алгоритм муравьиной колонии и т.д., не производилось. Результаты сравнения таких алгоритмов на сгенерированных случайных данных можно найти в работе.

Реализация и внедрение алгоритма

Такой алгоритм был реализован на языке 1С и был включен во внешнюю обработку под названием «Сжатие остатков», которая была подключена к WMS-системе. Мы не стали реализовывать алгоритм на языке С++ и использовать его из внешней Native компоненты, что было бы правильней, так как скорость работы кода на C++ в разы и на некоторых примерах даже в десятки раз превосходит скорость работы аналогичного кода на 1С. На языке 1С алгоритм был реализован для экономии времени на разработку и простоты отладки на рабочей базе заказчика. Результат работы алгоритма представлен на рисунке 5.

Рис.5. Обработка по «сжатию» остатков

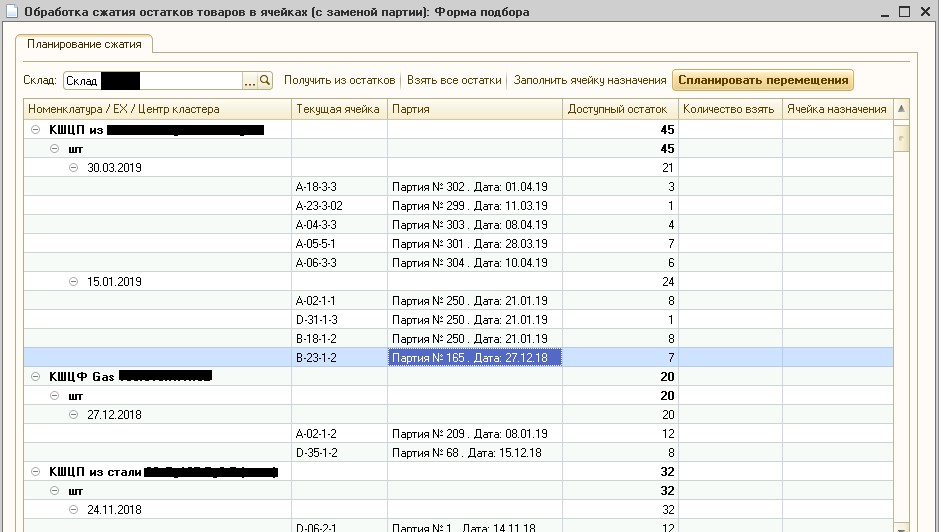
На рисунке 5 видно, что на указанном складе текущие остатки товаров в ячейках хранения разбились на кластеры, внутри которых даты партий товаров отличаются между собой не более чем на 30 дней. Так как заказчик производит и хранит на складе металлические шаровые краны, у которых срок годности исчисляется годами, то такой разницей дат можно пренебречь. Отметим, что в настоящее время такая обработка используется в продакшене систематически, и операторы WMS подтверждают хорошее качество кластеризации партий.

Выводы и продолжение

Главный опыт, который мы получили от решения такой практической задачи – это подтверждение эффективности использования парадигмы: мат. формулировка задачи $$ известная мат. модель $$ известный алгоритм $$ алгоритм с учетом специфики задачи. Дискретной оптимизации уже насчитывается более 300 лет и за это время люди успели рассмотреть очень много задач и накопить большой опыт по их решению. В первую очередь целесообразнее обратиться к этому опыту, а уж потом начинать изобретать свой велосипед.

В следующей статье мы продолжим рассказ о алгоритмах оптимизации и рассмотрим самое интересное и гораздо более сложное: алгоритм оптимального «сжатия» остатков в ячейках, который использует на входе данные, полученные от алгоритма кластеризации партий.

Статью подготовил
Роман Шангин, программист департамента проектов,
компания Первый БИТ, г. Челябинск