Пишем простую нейронную сеть с использованием математики и Numpy

Зачем очередная статья про то, как писать нейронные сети с нуля? Увы, я не смог найти статьи, где были бы описаны теория и код с нуля до полностью работающей модели. Сразу предупреждаю, что тут будет много математики. Я предполагаю, что читатель знаком с основами линейной алгебры, частными производными и хотя бы частично, с теорией вероятностей, а также Python и Numpy. Будем разбираться с полносвязной нейронной сетью и MNIST.

Математика. Часть 1 (простая)

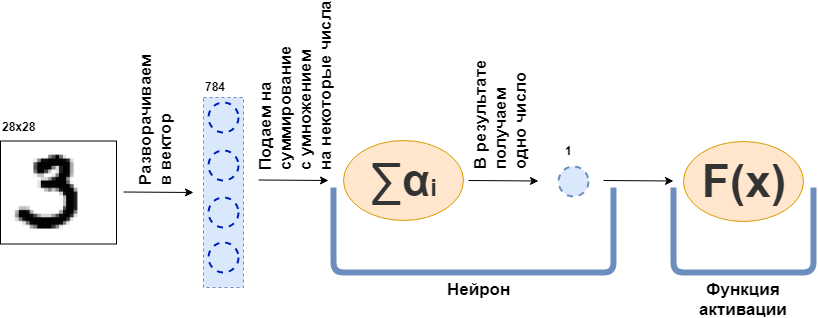
Что такое полносвязный слой (fully connected layer, FC layer)? Обычно говорят что-то в духе «Полносвязный слой — это слой, каждый нейрон которого соединён со всеми нейронами предыдущего слоя». Вот только непонятно что такое нейроны, как они соединены, особенно в коде. Сейчас я попробую разобрать это на примере. Вот пусть есть слой из 100 нейронов. Я знаю, что пока не объяснил, что это, но давайте просто представим, что есть 100 нейронов и у них есть вход, куда подаются данные, и выход, откуда они выдают данные. И на вход им подаётся чёрно-белая картинка 28х28 пикселей — всего 784 значения, если растянуть её в вектор. Картинку можно назвать входным слоем. Тогда чтобы каждый из 100 нейронов соединился с каждым «нейроном» или, если угодно, значением предыдущего слоя (то есть картинкой) нужно, чтобы каждый из 100 нейронов принял 784 значения исходной картинки. Например, для каждого из 100 нейронов достаточно будет умножить 784 значения картинки на какие-то 784 числа и сложить между собой, в результате выходит одно число. То есть это и есть нейрон:

$\$\$display\$\$\; ext\{Выход\; нейрона\}\; =\; ext\{какое-то\; число\}\_\{1\}\; cdot\; ext\{значение\; картинки\}\_1~+\; +~...~+~\; ext\{какое-то\; число\}\_\{784\}\; cdot\; ext\{значение\; картинки\}\_\{784\}\; \$\$display\$\$$

Тогда получится, что у каждого нейрона есть 784 числа, а всего этих чисел: (количество нейронов на этом слое) х (количество нейронов на предыдущем слое) = $\$inline\$100\; imes784\$inline\$$ = 78 400 цифр. Эти числа обычно называют весами слоя. Каждый нейрон выдаст свою число и в итоге получится 100-мерный вектор, и на самом деле можно записать, что этот 100-мерный вектор получается умножением 784-мерного вектора (нашей исходной картинки) на матрицу весов размером $\$inline\$100\; imes784\$inline\$$:

Дальше получившиеся 100 чисел передаются дальше, на функцию активации — некоторую нелинейную функцию — которая воздействует на каждое число поотдельности. Например, сигмоида, гиперболический тангенс, ReLU и другие. Функция активации обязательно нелинейная, иначе нейронная сеть научится только простым преобразованиям.

Затем получившиеся данные вновь подаются на полносвязный слой, но уже с другим количеством нейронов, и вновь на функцию активации. Так происходит несколько раз. Последний слой сети — это слой, который выдаёт ответ. В данном случае, ответ — это информация о том, какая цифра на картинке.

Во время обучения сети необходимо чтобы мы знали, какая цифра изображена на картинке. То есть чтобы датасет был размечен. Тогда можно использовать ещё один элемент — функцию ошибки. Она смотрит на ответ нейронной сети и сравнивает с настоящим ответом. Благодаря этому нейронная сеть и учится.

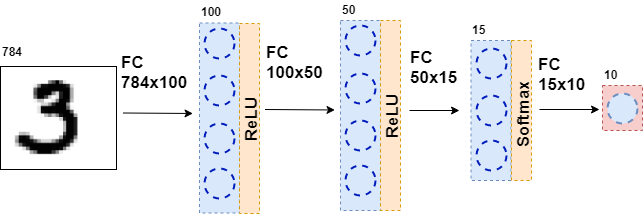
Общая постановка задачи

Весь датасет — это большой тензор (тензором будем называть некоторый многомерный массив данных) , где — i-ый объект, например, картинка, которая тоже является тензором. Для каждого объекта есть $\$inline\$y\_i\$inline\$$ — правильный ответ на i-м объекте. В этом случае нейронную сеть можно представить как некоторую функцию, которая принимает на вход объект и выдает на нем какой-то ответ:

Теперь давайте подробнее рассмотрим функцию . Так как нейронная сеть состоит из слоев, то каждый отдельный слой — функция. А значит

То есть, в самую первую функцию — первый слой — подается картинка в виде некоторого тензора. Функция $\$inline\$f\_1\$inline\$$ выдает какой-то ответ — тоже тензор, но уже другой размерности. Этот тензор будет называться внутреннем представлением. Теперь это внутреннее представление подается на вход функции $\$inline\$f\_2\$inline\$$, которая выдает свое внутреннее представление. И так далее, пока функция $\$inline\$f\_k\$inline\$$ — последний слой — не выдаст ответ $\$inline\$hat\{y\}\_i\$inline\$$.

Теперь, задача — обучить сеть — сделать так, чтобы ответ сети совпадал с правильным ответом. Для начала нужно измерить насколько нейронная сеть ошиблась. Измерять это будет функция ошибки $\$inline\$L(hat\{y\}\_i,\; y\_i)\$inline\$$. Причем накладываем ограничения:

1. $\$inline\$hat\{y\}\_i\; xrightarrow\{\}\; y\_i\; Rightarrow\; L(hat\{y\}\_i,\; y\_i)\; xrightarrow\{\}\; 0\$inline\$$
2. $\$inline\$exists\; ~\; dL(hat\{y\}\_i,\; y\_i)\$inline\$$
3. $\$inline\$L(hat\{y\}\_i,\; y\_i)\; geq\; 0\$inline\$$

Ограничение 2 наложим на все функции слоев $\$inline\$f\_j\$inline\$$ — пусть они все будут дифференцируемы.

Причем, на самом деле (об этом я умолчал) часть этих функции зависят от параметров — весов нейронной сети — . И вся идея заключается в том, чтобы подобрать такие веса, чтобы $\$inline\$hat\{y\}\_i\$inline\$$ совпадал с $\$inline\$y\_i\$inline\$$ на всех объектах датасета. Отмечу, что веса есть не во всех функциях.

Итак, на чем мы остановились? Все функции нейронной сети дифференцируемы, функция ошибки тоже дифференцируема. Вспомним одно из свойств градиента — показывать направление роста функции. Воспользуемся этим, ограничениями 1 и 3, фактом, что

и тем, что я умею считать частные производные и производные сложной функции. Теперь есть все что нужно, для того чтобы посчитать

для любого i и j. Эта частная производная показывает направление, в котором нужно изменить , чтобы увеличить $\$inline\$L\$inline\$$. Чтобы уменьшить нужно сделать шаг в сторону , ничего сложного.

Значит процесс обучения сети строится так: несколько раз в цикле проходим по всему датасету (это называется эпоха), для каждого объекта датасета считаем $\$inline\$L(hat\{y\}\_i,\; y\_i)\$inline\$$ (это называется forward pass) и считаем частную производную $\$inline\$partial\; L\$inline\$$ для всех весов , затем обновляем веса (это называется backward pass).

Замечу, что я еще не ввел никаких конкретных функций и слоев. Если на данном этапе не совсем ясно, что со всем этим делать, предлагаю продолжить чтение — математики станет больше, но теперь она будет идти с примерами.

Математика. Часть 2 (сложная)

Функция ошибки

Я начну с конца и выведу функцию ошибки для задачи классификации. Для задачи регрессии вывод функции ошибки хорошо описан в книге «Глубокое обучение. Погружение в мир нейронных сетей».

Для простоты, есть нейронная сеть (NN), которая отделяет фотографии котиков от фотографий собак, и есть набор фотографий кошек и собак, для которых есть правильный ответ $\$inline\$y\_\{true\}\$inline\$$.

$\$\$display\$\$NN(picture\; |\; Omega)\; =\; y\_\{pred\}\$\$display\$\$$

Все что я буду делать дальше, очень похоже на метод максимального правдоподобия. Поэтому основная задача — найти функцию правдоподобия. Если опустить подробности, то такую функцию, которая сопоставляет предсказание нейронной сети и правильный ответ, и, если они совпадают, выдает большое значение, если же нет, наоборот. На ум приходит вероятность правильного ответа при заданных параметрах:

$\$\$display\$\$p(y\_\{pred\}\; =\; y\_\{true\}\; |\; Omega)\$\$display\$\$$

А теперь сделаем некоторый финт, который вроде бы ни от куда не следует. Пусть нейронная сеть выдает ответ в виде двумерного вектора, сумма значений которого равна 1. Первый элемент этого вектора можно назвать мерой уверенности, что на фотографии кот, а второй элемент — мерой уверенности, что на фотографии пёс. Да это же почти вероятности!

Теперь функцию правдоподобия можно переписать в виде:

$\$\$display\$\$p(y\_\{pred\}\; =\; y\_\{true\}\; |\; Omega)\; =\; p\_Omega\; (y\_\{pred\})^t\_\{0\}\; *\; (1\; -\; p\_Omega\; (y\_\{pred\}))^t\_\{1\}\; =\; p\_0^\{t\_0\}\; *\; p\_1^\{t\_1\}\$\$display\$\$$

Где $\$inline\$t\_0,\; t\_1\$inline\$$ метки верного класса, например, если $\$inline\$y\_\{true\}\; =\; cat\$inline\$$, то $\$inline\$t\_0\; ==\; 1,\; t\_1\; ==\; 0\$inline\$$, если $\$inline\$y\_\{true\}\; =\; dog\$inline\$$, то $\$inline\$t\_0\; ==\; 0,\; t\_1\; ==\; 1\$inline\$$. Таким образом всегда рассматривается вероятность класса, который должен был быть предсказан нейронной сетью (но не обязательно был предсказан ею). Теперь это можно обобщить на любое количество классов (например, m классов):

$\$\$display\$\$p(y\_\{pred\}\; =\; y\_\{true\}\; |\; Omega)\; =\; prod\_0\; ^m\; p\_i^\{t\_i\}\$\$display\$\$$

Однако, в любом датасете есть много объектов (например, N объектов). Хочется, чтобы на каждом или большинстве объектов нейронная сеть выдавала верный ответ. И для этого нужно перемножить результаты формулы выше для каждого объекта из датасета.

$\$\$display\$\$MaximumLikelyhood\; =\; prod\_\{j=0\}\; ^N\; prod\_\{i=0\}\; ^m\; p\_\{i,j\}^\{t\_\{i,j\}\}\$\$display\$\$$

Чтобы получить хорошие результаты, эту функцию нужно максимизировать. Но, во-первых, минимизировать круче, потому что у нас есть стохастический градиентный спуск и все плюшки для него — просто припишем минус, а, во-вторых, с огромным произведением работать затруднительно — логарифмируем.

$\$\$display\$\$CrossEntropyLoss\; =\; -\; sumlimits\_\{j=0\}^\{N\}\; sumlimits\_\{i=0\}^\{m\}t\_\{i,j\}cdotlog(p\_\{i,j\})\$\$display\$\$$

Замечательно! Получилась перекрестная энтропия или, в бинарном случае, logloss. Эту функцию легко считать и еще легче дифференцировать:

Дифференцировать нужно для алгоритма обратного распространения ошибки. Замечу, что функция ошибки не изменяет размерность вектора. Если, как в случае MNIST, на выходе получается 10-мерный вектор ответов, то и при вычислении производной получится 10-мерный вектор производных. Ещё одна интересная вещь то, что только один элемент производной не будет равен нулю, при котором $\$inline\$t\_\{i,j\}\; eq\; 0\$inline\$$, то есть при правильном ответе. И чем меньше вероятность верного ответа предсказала нейронная сеть на данном объекте, тем больше на нем будет функция ошибки.

Функции активации

На выходе каждого полносвязного слоя нейронной сети обязательно должна присутствовать нелинейная функция активации. Без неё невозможно обучить содержательную нейронную сеть. Если забежать вперед, то полносвязный слой нейронной сети — это просто умножение входных данных на матрицу весов. В линейной алгебре это называется линейным отображением — некоторая линейная функция. Комбинация линейных функций — тоже линейная функция. Но это значит, что такая функция может аппроксимировать только линейные функции. Увы, это не то, зачем нужны нейронные сети.

Softmax

Обычно эта функция используется на последнем слое сети, так как она превращает вектор с последнего слоя в вектор «вероятностей»: каждый элемент вектора лежит от 0 до 1 и их сумма равна 1. Она не меняет размерность вектора.

$\$\$display\$\$Softmax\_i\; =\; frac\{e^\{x\_i\}\}\{sum\; limits\_\{j\}\; e^\{x\_j\}\}\$\$display\$\$$

Теперь перейдем к поиску производной. Так как — вектор, и в знаменателе всегда присутствуют все его элементы, то при взятии производной получим якобиан:

Теперь про backpropagation. От предыдущего слоя (обычно это функция ошибки) приходит вектор производных . В случае если пришел от функции ошибки на MNIST, — 10-мерный вектор. Тогда якобиан имеет размерность 10х10. Чтобы получить , который пойдет далее, на предыдущий слой (не забываем, что мы идем от конца к началу сети при обратном распространении ошибки), нужно умножить на $\$inline\$J\_\{Softmax\}\$inline\$$ (строка на столбец):

На выходе получаем 10-мерный вектор производных .

ReLU

Массово использовать ReLU стали после 2011 года, когда вышла статья «Deep Sparse Rectifier Neural Networks». Однако, такая функция была известна и ранее. К ReLU применимо такое понятие, как «сила активации» (подробнее об этом можно почитать в книге «Глубокое обучение. Погружение в мир нейронных сетей»). Но главная особенность, которая делает ReLU привлекательнее других функций активации — простое вычисление производной:

Таким образом ReLU вычислительно эффективнее других функций активации (сигмоида, гиперболический тангенс и др.).

Полносвязный слой

Теперь время обсудить полносвязный слой. Наиболее важный из всех остальных, потому что именно в этом слое находятся все веса, которые и нужно настроить для того, чтобы нейронная сеть работала хорошо. Полносвязный слой это просто-напросто матрица весов:

$\$\$display\$\$W\; =\; |w\_\{i,j\}|\$\$display\$\$$

Новое внутреннее представление получается, когда матрица весов умножается на столбец входных данных:

Где имеет размер $\$inline\$input\backslash \_shape\$inline\$$, а $\$inline\$x\_\{new\}\$inline\$$ — $\$inline\$output\backslash \_shape\$inline\$$. Например, — 784-мерный вектор, а — 100-мерный вектор, тогда матрица W имеет размер 100х784. Получается, что на этом слое находится 100х784 = 78 400 весов.

При обратном распространении ошибки нужно взять производную по каждому весу этой матрицы. Упростим задачу и возьмем только производную по $\$inline\$w\_\{1,1\}\$inline\$$. При умножении матрицы и вектора первый элемент нового вектора равен $\$inline\$x\_\{new~1\}\; =\; w\_\{1,1\}\; cdot\; x\_1\; +\; ...\; +\; w\_\{1,784\}\; cdot\; x\_\{784\}\; \$inline\$$, а производная $\$inline\$x\_\{new~1\}\$inline\$$ по $\$inline\$w\_\{1,1\}\$inline\$$ будет просто $\$inline\$x\_1\$inline\$$, нужно всего лишь взять производную от суммы выше. Аналогично происходит для всех остальных весов. Но это еще не алгоритм обратного распространения ошибки, пока это просто матрица производных. Нужно вспомнить, что от следующего слоя на этот (ошибка идет от конца к началу) приходит 100-мерный вектор градиента . Первый элемент этого вектора $\$inline\$dz\_1\; \$inline\$$ будет умножаться на все элементы матрицы производных, которые «участвовали» в создании $\$inline\$x\_\{new~1\}\$inline\$$, то есть на $\$inline\$x\_1,\; x\_2,\; ...\; ,\; x\_\{784\}\$inline\$$. Аналогично и остальные элементы. Если перевести это на язык линейной алгебры, то это записывается так:

На выходе получается матрица 100х784.

Теперь нужно понять, что же передавать на предыдущий слой. Для этого и для большего понимания что вообще сейчас произошло, я хочу записать то, что случилось при взятии производных на этом слое чуть-чуть другим языком, уйти от конкретики «что на что умножается» к функциям (опять). Когда я хотел настроить веса, то я хотел взять производную функции ошибки по этим весам: $\$inline\$frac\{partial\; L\}\{partial\; W\}\$inline\$$. Выше было показано, как брать производные по функциям ошибки и функциям активации. Поэтому можно рассмотреть такой случай (в уже сидят все производные от функции ошибки и функций активации):

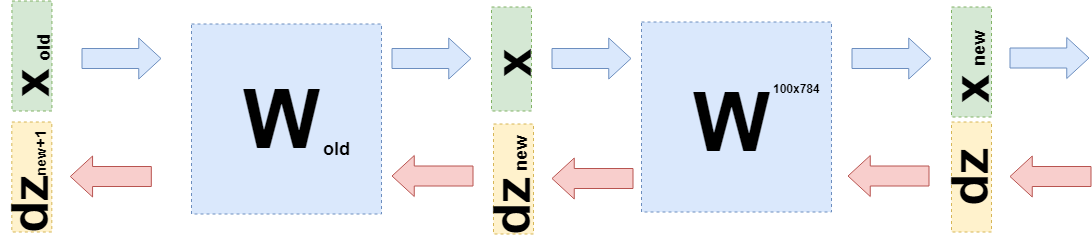
Так можно сделать, потому что можно рассмотреть , как функцию от W: .
Можно подставить это в формулу выше:

Где E матрица состоящая из единиц (НЕ единичная матрица).
Теперь когда нужно взять производную от предыдущего слоя (пусть для простоты выкладок это тоже будет полносвязный слой, но в общем случае это ничего не меняет), то нужно рассмотреть , как функцию от предыдущего слоя :

Именно и нужно отправить на предыдуший слой.

Код

В первую очередь эта статья нацелена на объяснение математики нейронных сетей. Коду я уделю совсем немного времени.

Это пример реализации функции ошибки:

class CrossEntropy:     def forward(self, y_true, y_hat):         self.y_hat = y_hat         self.y_true = y_true         self.loss = -np.sum(self.y_true * np.log(y_hat))         return self.loss      def backward(self):         dz = -self.y_true / self.y_hat         return dz 

Класс имеет методы для прямого и обратного прохода. В момент прямого прохода экземпляр класса сохраняет данные внутри слоя, а в момент обратного прохода использует их для расчета градиента. Таким же образом построены и остальные слои. Благодаря этому становится возможным написать полносвязную нейронную в таком стиле:

class MnistNet:     def __init__(self):         self.d1_layer = Dense(784, 100)         self.a1_layer = ReLu()         self.drop1_layer = Dropout(0.5)          self.d2_layer = Dense(100, 50)         self.a2_layer = ReLu()         self.drop2_layer = Dropout(0.25)          self.d3_layer = Dense(50, 10)         self.a3_layer = Softmax()     def forward(self, x, train=True):         ...     def backward(self,                  dz,                  learning_rate=0.01,                  mini_batch=True,                  update=False,                  len_mini_batch=None):         ... 

Полный код можно посмотреть тут. Также советую изучить эту статью на Хабре.

Заключение

Надеюсь, я смог объяснить и показать, что за нейронными сетями стоит довольно простая математика и, что это совершенно не страшно. Тем не менее для более глубокого понимания стоит попробовать написать свой «велосипед». Исправления и предложения с радостью почитаю в комментариях.